Reflection of plane seismic waves at the surface of double-porosity dual-permeability materials

Abstract

The present work deals with the reflection of plane seismic waves at the stress-free plane surface of double-porosity dual-permeability material. The incidence of two main waves (i.e., P₁ and SV) is considered. As a result of the incident waves, four reflected (three longitudinal and one shear) waves are found in the medium. The expressions of reflection coefficients for a given incident wave are obtained as a non-singular system of linear equations. The energy shares of reflected waves are obtained in the form of an energy matrix. A numerical example is considered to calculate the partition of incident energy for fully closed as well as perfectly open pores. Effect of incident direction on the partition of the incident energy is analyzed with the change in wave frequency, wave-induced fluid-flow, pore-fluid viscosity and double-porosity structure. It has been confirmed from the numerical interpretation that during the reflection process, conservation of incident energy is obtained at each angle of incidence.

1 Introduction

Most of the earth’s materials such as rocks are generally heterogeneous, porous and fractured (cracked) in nature. Generally, in situ rocks, pores and crack (fracture) space may be filled with oil, gas or water. These fluids play a significant role in the daily life of human beings. The key issues faced by reservoir engineers are how to distinguish these fluids and to understand their flow characteristics. The phenomenon of reflection is of great importance (practically as well as theoretically) in various scientific fields, such hydrogeology, engineering geology, seismology and petroleum geophysics. The process of reflection (i.e., incident energy reflected back from the interface) occurs due to the discontinuity encountered at the interface of materials. In exploration geophysics and seismology, seismic (reflection phenomenon) methods are used to analyze the fluid content in subsurface reservoirs. The evaluation of reservoir rocks is carried on the basis of reflected wave signals.

It is generally observed that realistic heterogeneous reservoirs have a dual-porosity network, one is matrix porosity and the other is fracture porosity. The matrix (storage) porosity occupies most of the volume of the reservoir while fracture (crack) porosity occupies very little volume. These two porosities are distinguished on the basis of permeability as the fracture (crack) permeability is greater than the matrix permeability. Double-porosity dual-permeability material theory plays an important role in the characterization of highly fractured reservoirs. The extension of Biot’s poroelasticity (Biot 1956, 1962a, b) to double-porosity solids was carried out by Berryman and Wang (1995, 2000). They derived the phenomenological equations for a double-porosity/dual-permeability medium. They found that three longitudinal and one shear wave exist in the double-porosity medium. Later, Pride (2003) and Pride and Berryman (2003) modified the governing equations developed by Berryman and Wang (1995, 2000) for mesoscopic fluid-flow in double-porosity dual-permeability materials by using the volume averaging technique. Based on the Berryman and Wang theory, the wave propagation at the boundary of double-porosity media was investigated by Dai et al. (2006) and Dai and Kuang (2008). In recent years, the main credit goes to Sharma (2013, 2014, 2015a, b, 2016, 2017a, b) for comprehensive discussion of wave propagation in double-porosity solids. Sharma (2017a) studied the effects of wave frequency, wave inhomogeneity, pore-fluid viscosity and skeletal permeability on the propagation and attenuation of waves in double-porosity dual-permeability materials. Sharma (2017b) studied the propagation and attenuation of inhomogeneous waves in double-porosity dual-permeability materials. He graphically analyzed the effects of pore-fluid viscosity, wave inhomogeneity and composition of double porosity on inhomogeneous propagation of waves. He also studied the variations in the fluid-flow profile for different values of pore-fluid viscosity, skeleton permeability, wave frequency and wave inhomogeneity.

To the best of our knowledge, the problem of reflection of plane waves at the surface of double-porosity dual-permeability materials has not yet been investigated. In the present work, the complete reflection phenomenon at the surface of double-porosity dual-permeability materials is investigated. The incidence of two main waves (i.e., P₁ and SV) is considered. As a result of the incident wave, four reflected (three longitudinal and one shear) waves are found in the medium. The expressions of reflection coefficients for a given incident wave are obtained as a non-singular system of linear equations. The energy shares of reflected waves are obtained in the form of an energy matrix. A numerical example is considered to calculate the partition of incident energy for fully closed as well as perfectly open pores. The effect of incident direction on the partition of incident energy is analyzed with the changes in wave frequency, wave-induced fluid-flow, pore-fluid viscosity and double-porosity structure. It has been confirmed from the numerical interpretation that during the reflection process, at each angle of incidence, conservation of incident energy is obtained in the presence of interaction energy.

2 Constitutive relations

The linear constitutive relations for double-porosity dual-permeability materials are defined as (Pride and Berryman 2003; Sharma 2017a)

$$\begin{aligned} \sigma_{ij} & = \left\{ {\left( {b_{11} - \frac{2}{3}G} \right)\nabla \cdot u + b_{12} \nabla \cdot v + b_{13} \nabla \cdot w} \right\}I \\ & \quad + \,G(u_{i,j} + u_{j,i} ), \\ \end{aligned}$$

(1)

$$- p_{f1} = \left\{ {b_{12} \nabla \cdot u + b_{22} \nabla \cdot v + b_{23} \nabla \cdot w} \right\}I,$$

(2)

$$- p_{f2} = \left\{ {b_{13} \nabla \cdot u + b_{23} \nabla \cdot v + b_{33} \nabla \cdot w} \right\}I,$$

(3)

where u, v and w define the averaged displacement of solid and averaged displacement of pore-fluid particles relative to solid in the first and second porous phase, respectively. σ_ij is the stress tensor and (p_f1, p_f2) are pore fluid-pressures in two porous phases. In the presence of wave-induced fluid flow (WIFF), the anelastic coefficients b_ij are defined as (Sharma 2017a)

$$\begin{aligned} b_{ij} & = c_{ij} - \frac{{(c_{i2} - c_{i3} )(c_{j2} - c_{j3} )}}{{c_{22} + c_{33} - 2c_{23} - {{\iota \omega } \mathord{\left/ {\vphantom {{\iota \omega } {\gamma (\omega )}}} \right. \kern-0pt} {\gamma (\omega )}}}};\quad \gamma (\omega ) = \gamma_{0} \sqrt {1 - \iota \frac{\omega }{{\omega_{c} }};} \\ \gamma_{0} & = \frac{{\nu_{1} \kappa_{11} }}{{\eta L_{1}^{2} }};\quad \omega_{c} = \frac{{\eta B_{1} K_{1} }}{{\kappa_{11} \alpha_{1} }}\left( {\frac{V}{S}\gamma_{0} } \right)^{2} ;\quad \frac{V}{S} = \frac{{R^{3} }}{{3r^{2} }}, \\ \end{aligned}$$

where $\frac{V}{S}$ measures the volume to surface ratio of phase 2 as embedded in phase 1, r is the radius of the sphere (phase 2) which is included at the center of the sphere (phase 1) of radius R. L₁ denotes the average distance over which a fluid-pressure gradient exists in phase 1, in the final stages of equilibration (Pride 2003). In the absence of wave-induced fluid flow (WIFF), the anelastic coefficients b_ij = c_ij. The elastic coefficients c_ij are defined as inverse of the symmetric compliance tensor a_ij. The symmetric compliance tensors a_ij, i, j = 1, 2, 3, are related to the various measurable quantities of the porous aggregate as given in Sharma (2017a).

3 Wave propagation

Sharma (2017a) has already studied the propagation of plane harmonic waves in double-porosity dual-permeability (DP²) materials. He found that four (three longitudinal and one shear) waves exist in such a medium. The roots of the cubic equations (Sharma 2017a) represent the propagation of three longitudinal waves (P₁, P₂, P₃) with complex velocities (ς₁, ς₂, ς₃). The polarizations (or displacements) of fluid particles in two porosities for longitudinal waves are given by Sharma (2017a)

$$\begin{aligned} v_{j} & = \frac{{b_{0} \varsigma^{4} + b_{1} \varsigma^{2} + b_{2} }}{{a_{0} \varsigma^{4} + a_{1} \varsigma^{2} + a_{2} }}u_{j} , \\ w_{j} & = \frac{{c_{0} \varsigma^{4} + c_{1} \varsigma^{2} + c_{2} }}{{a_{0} \varsigma^{4} + a_{1} \varsigma^{2} + a_{2} }}u_{j} ,\quad (j = 1,2,3). \\ \end{aligned}$$

(4)

The complex velocity (ς₄) of the long transverse wave is given by $\varsigma_{4}^{2} = G/(\rho + \frac{{b_{0} }}{{a_{0} }}\rho_{f} + \frac{{c_{0} }}{{a_{0} }}\rho_{f} )$. The polarizations (or displacements) of fluid particles in two porosities for this wave are given by

$$v_{j} = \frac{{b_{0} }}{{a_{0} }}u_{j} ,\quad w_{j} = \frac{{c_{0} }}{{a_{0} }}u_{j} ,\quad (j = 1,2,3).$$

(5)

The various coefficients occurring in the above expressions are given in Sharma (2017a).

4 Reflection at a plane boundary

4.1 Formulation of the problem

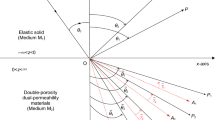
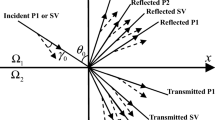
Consider a rectangular coordinate system (x, y, z), in which half-space z > 0 is occupied by DP² materials with their depth increasing along the z-direction. The plane z = 0 is considered as a stress-free surface of this medium. A plane harmonic wave propagates with velocity ς₀ and angular frequency ω is incident at the boundary z = 0 with an angle of incidence θ₀. Consequently, four reflected waves (i.e., P₁, P₂, P₃, SV) are observed in DP² materials.

4.2 Displacements

Following Sharma (2013), the displacement of material particles is the sum of displacements associated with the incident wave and four reflected waves. Hence, for two-dimensional motions in the xz-plane, the general displacement of material particles is expressed as

$$\begin{aligned} u_{j} & = \left[ {A_{j}^{(0)} \exp (\iota \omega (sx + q_{0} z - t)} \right. \\ & \quad \left. { + \sum\limits_{k = 1}^{4} {f_{k} A_{j}^{(k)} \exp \{ \iota \omega (sx + q_{k} z - t)\} } } \right], \\ v_{j} & = \left[ {B_{j}^{(0)} \exp (\iota \omega (sx + q_{0} z - t)} \right. \\ & \quad \left. { + \sum\limits_{k = 1}^{4} {f_{k} B_{j}^{(k)} \exp \{ \iota \omega (sx + q_{k} z - t)\} } } \right], \\ w_{j} & = \left[ {C_{j}^{(0)} \exp (\iota \omega (sx + q_{0} z - t)} \right. \\ & \quad \left. { + \sum\limits_{k = 1}^{4} {f_{k} C_{j}^{(k)} \exp \{ \iota \omega (sx + q_{k} z - t)\} } } \right],\quad (j = x,z), \\ \end{aligned}$$

(6)

where f_k is the excitation factors for the reflected wave relative to the incident wave. The coefficients A ^{( k)} _j , B ^{( k)} _j and C ^{( k)} _j represent the polarization for the motion of solid particles and fluid particles in two porous phases, respectively. These coefficients are defined on the basis of Eqs. (4) and (5). The index ‘0’ represents the incident wave. The index ‘k’ (= 1, 2, 3, 4) represent, respectively, the reflected (P₁, P₂, P₃, SV) waves. The horizontal slowness (s), in terms of angle of propagation (θ₀), angle of attenuation (γ₀), propagation vector ($\vec{P}$) and attenuation vector ($\vec{A}$), is defined as (Borcherdt 2009)

$$s = \left| {\vec{P}} \right|\sin \theta_{0} - \iota \left| {\vec{A}} \right|\sin (\theta_{0} - \gamma_{0} ),$$

(7)

where, for incident wave of velocity ς₀, we have

$$\left| {\vec{P}} \right|^{2} = \frac{1}{2}\left[ {\text{Re} \left( {\frac{{\omega^{2} }}{{\varsigma_{0}^{2} }}} \right) + \sqrt {\left( {\text{Re} \left( {\frac{{\omega^{2} }}{{\varsigma_{0}^{2} }}} \right)} \right)^{2} + {{\left( {\text{Im} \left( {\frac{{\omega^{2} }}{{\varsigma_{0}^{2} }}} \right)} \right)^{2} } \mathord{\left/ {\vphantom {{\left( {\text{Im} \left( {\frac{{\omega^{2} }}{{\varsigma_{0}^{2} }}} \right)} \right)^{2} } {\cos^{2} \gamma_{0} }}} \right. \kern-0pt} {\cos^{2} \gamma_{0} }}} } \right],$$

(8)

$$\left| {\vec{A}} \right|^{2} = \frac{1}{2}\left[ { - \text{Re} \left( {\frac{{\omega^{2} }}{{\varsigma_{0}^{2} }}} \right) + \sqrt {\left( {\text{Re} \left( {\frac{{\omega^{2} }}{{\varsigma_{0}^{2} }}} \right)} \right)^{2} + {{\left( {\text{Im} \left( {\frac{{\omega^{2} }}{{\varsigma_{0}^{2} }}} \right)} \right)^{2} } \mathord{\left/ {\vphantom {{\left( {\text{Im} \left( {\frac{{\omega^{2} }}{{\varsigma_{0}^{2} }}} \right)} \right)^{2} } {\cos^{2} \gamma_{0} }}} \right. \kern-0pt} {\cos^{2} \gamma_{0} }}} } \right].$$

(9)

The incident medium is dissipative due to the presence of viscosity in pore fluid. Therefore, all the waves (i.e., incident and reflected) are attenuated (i.e., different directions of propagation and attenuation) in nature due to the dissipative nature of the medium. Hence, the incident wave at the boundary z = 0 is specified through its propagation direction (θ₀) and attenuation direction (γ₀). The vector (s, 0, q₀) specifies the slowness vector of the incident wave, where $q_{0} ( = \pm \sqrt {\varsigma_{0}^{2} - s^{2} } )$ is the vertical slowness of incident wave. To ensure the propagation of the incident wave toward the boundary (i.e., negative z-direction), we must have R(q₀) < 0. According to Snell’s law, the horizontal slowness(s) of both incident and reflected waves will remain same. Then, the vector (s, 0, q_k) specifies the slowness vector for reflected waves, where $q_{k} ( = \pm \sqrt {\varsigma_{k}^{2} - s^{2} } )$, (k = 1, 2, 3, 4). To assure the decay of reflected waves moving away from boundary (i.e., positive z-direction), we must have I(q_k) > 0. To define polarization of a longitudinal and transverse wave, the required unit vector $\hat{n}$ is obtained as $\hat{n} = (s,\,0,\,q_{k} )\,\,\varsigma_{k}$.

4.3 Boundary conditions

In the present geometry, two types of boundary conditions are considered at the stress-free surface z = 0 of DP² materials. One of them is an impermeable boundary (sealed pores), and the other is a permeable boundary (fully opened pores). On the basis of Sharma (2013), the appropriate boundary conditions at the plane interface z = 0 are

$$\begin{array}{*{20}l} {({\text{i}})} \hfill & {\sigma_{zz} = 0,} \hfill \\ {({\text{ii}})} \hfill & {\sigma_{zx} = 0,} \hfill \\ {({\text{iii}})} \hfill & {\xi \,T_{0} \,\dot{v}_{z} - (1 - \xi )p_{f1} = 0,} \hfill \\ {({\text{iv}})} \hfill & {\xi \,T_{0} \,\dot{w}_{z} - (1 - \xi )p_{f2} = 0} \hfill \\ \end{array}$$

(10)

where T₀ is a scaling parameter that ensures dimensional homogeneity. The parameter ξ = 1 defines the impermeable boundary (sealed surface pores) and ξ = 0 defines the permeable boundary (fully opened surface pores).

4.4 Reflection coefficients

We obtain a system of four simultaneous non-homogeneous linear equations after solving the four boundary conditions (10) using displacements defined in Eq. (6). The system of four equations is given by

$$\sum\limits_{k = 1}^{4} {H_{lk} f_{k} = - H_{l0} } ,\quad (l = 1,\,2,\,3,\,4)$$

(11)

For k = 1, 2, 3, 4, we have

$$\begin{aligned} H_{1k} & = (b_{11} - 2G/3)\left[ {sA_{x}^{(k)} + q_{k} A_{z}^{(k)} } \right] + b_{12} \left[ {sB_{x}^{(k)} + q_{k} B_{z}^{(k)} } \right] \\ & \quad + \,b_{13} \left[ {sC_{x}^{(k)} + q_{k} C_{z}^{(k)} } \right] + 2Gq_{k} A_{z}^{(k)} , \\ H_{2k} & = G\left[ {q_{k} A_{x}^{(k)} + sA_{z}^{(k)} } \right], \\ H_{3k} & = \xi T_{0} B_{z}^{(k)} - \left( {1 - \xi } \right)Y_{k} , \\H_{4k} &= \xi T_{0} C_{z}^{(k)} - \left( {1 - \xi } \right)Z_{k} , \\ \end{aligned}$$

where Y_k = b₁₂[sA ^{( k)} _x  + q_kA ^{( k)} _z ] + b₂₂[sB ^{( k)} _x  + q_kB ^{( k)} _z ] + b₂₃[sC ^{( k)} _x  + q_kC ^{( k)} _z ]

and

Z_k = b₁₃[sA ^{( k)} _x  + q_kA ^{( k)} _z ] + b₂₃[sB ^{( k)} _x  + q_kB ^{( k)} _z ] + b₃₃[sC ^{( k)} _x  + q_kC ^{( k)} _z ].

System (11) is solved for four unknowns f_k (k = 1, 2, 3, 4) by using the Gauss elimination method. These unknowns may be treated as reflection coefficients.

4.5 Energy partition

In this article, our aim is to study the distribution of incident energy among distinct reflected waves at the surface element of unit area at the stress-free surface z = 0. According to Achenbach (1973), the rate at which energy is communicated per unit area of the surface (i.e., energy flux across the surface element) is the scalar product of surface traction and particle velocity, denoted by Q. For DP² materials, the average rate of energy transmission at z = 0 is given by

$$\left\langle {Q_{jk} } \right\rangle = \frac{1}{2}R\left[ {\sigma_{zz}^{(j)} \,\bar{\dot{u}}_{z}^{(k)} + \sigma_{zx}^{(j)} \,\bar{\dot{u}}_{x}^{(k)} + ( - p_{f1}^{(j)} )\bar{\dot{u}}_{z}^{(k)} + ( - p_{f2}^{(j)} )\bar{\dot{w}}_{z}^{(k)} } \right],$$

(12)

where a bar over a quantity defines its complex conjugate.

The concept of interaction energy (Borcherdt 2009; Krebes 1983) or the interference energy (Ainslie and Burns 1995) between two dissimilar waves is also involved due to the dissipative nature of double-porosity dual-permeability materials. Thus, when a plane wave impinges at the plane interface z = 0, then in addition to the energy transmitted to reflected waves, some finite amount of energy is carried toward (negative value of interaction energy) and away from (positive value of interaction energy) the interface due to the interaction of incident wave and reflected waves, and of reflected wave themselves. In the present geometry, the medium supports the propagation of five waves (one incident and four reflected). Hence, to describe the distribution of incident energy at the surface z = 0, an energy matrix is defined as

$$E_{lk} = {{R\left( {\left\langle {Q_{lk} } \right\rangle f_{l} \,\bar{f}_{k} } \right)} \mathord{\left/ {\vphantom {{R\left( {\left\langle {Q_{jk} } \right\rangle f_{l} \,\bar{f}_{k} } \right)} {R\left( {\left\langle {Q_{55} } \right\rangle } \right)}}} \right. \kern-0pt} {R\left( {\left\langle {Q_{55} } \right\rangle } \right)}},\quad (l,k = 1, \, 2, \, 3, \, 4, \, 5);$$

(13)

where f₅ = 1. The elements $\left\langle {Q_{lk} } \right\rangle$ in Eq. (13) are given by

$$\begin{aligned} \left\langle {Q_{lk} } \right\rangle & = \left[ {(b_{11} - 2G/3)\left[ {sA_{x}^{(l)} + q_{l} A_{z}^{(l)} } \right] + b_{12} \left[ {sB_{x}^{(l)} + q_{l} B_{z}^{(l)} } \right]} \right. \\ & \left. {\quad + \,b_{13} \left[ {sC_{x}^{(l)} + q_{l} C_{z}^{(l)} } \right] + 2Gq_{l} A_{z}^{(l)} } \right]{\mkern 1mu} {\mkern 1mu} \bar{A}_{z}^{(k)} + G\left[ {sA_{x}^{(l)} + q_{l} A_{z}^{(l)} } \right]{\mkern 1mu} \bar{A}_{x}^{(k)} \\ & \quad + \left[ {b_{12} \left[ {sA_{x}^{(l)} + q_{l} A_{z}^{(l)} } \right] + b_{22} \left[ {sB_{x}^{(l)} + q_{l} B_{z}^{(l)} } \right] + b_{23} \left[ {sC_{x}^{(l)} + q_{l} C_{z}^{(l)} } \right]} \right]{\mkern 1mu} \bar{B}_{z}^{(k)} \\ & \quad + \left[ {b_{13} \left[ {sA_{x}^{(l)} + q_{l} A_{z}^{(l)} } \right] + b_{23} \left[ {sB_{x}^{(l)} + q_{l} B_{z}^{(l)} } \right] + b_{33} \left[ {sC_{x}^{(l)} + q_{l} C_{z}^{(l)} } \right]} \right]{\mkern 1mu} \bar{C}_{z}^{(k)}. \\ \end{aligned}$$

(14)

The energy matrix E_ij, (i, j = 1, 2, 3, 4, 5), calculates the energy shares of reflected waves in DP² materials. The diagonal entries E₁₁, E₂₂, E₃₃ and E₄₄ identify the energy shares of reflected P₁, P₂, P₃ and SV waves, respectively. The interaction energy due to the interference of each reflected wave with the incident wave is given by $E_{\text{IR}} \, = \,\sum_{i = 1}^{4} \left( {E_{5i} \, + \,E_{i5} } \right)$. The interaction energy due to the interference between each pair of reflected waves is given by $E_{\text{RR}} \, = \,\sum _{i = 1}^{4} \left( {\sum_{j = 1}^{4} \left( {E_{ij} \, + \,E_{ji} } \right)} \right)$. Thus, for energy conservation at the interface z = 0, we have $\sum_{l = 1}^{5} \sum_{k = 1}^{5} E_{lk} \, = \,0$.

5 Numerical results and discussion

5.1 Numerical example

We consider the distribution of incident energy among reflected waves at the stress-free surface of double-porosity dual-permeability materials. DP² materials consisting of two distinct porous phases, both saturated with same viscous fluid. It is assumed that each sphere of DP² composite of radius R contains at its center a small sphere of radius r of phase 2. In this example, a parameter ɛ = r/R is used to define ν₂ = ɛ³, ν₁ = 1 − ɛ³ and V/S = R³/(3r²) = r/(3ɛ³). Then, from Pride and Berryman (2003) $L_{1}^{2} = \left( {\frac{r}{\varepsilon }} \right)^{2} \left( {\frac{9}{14} - \frac{3}{4}\varepsilon } \right)$. The value chosen for k₁₂ = k₂₁ is 10⁻²⁰ m². The bulk moduli (K₁, K₂) for two porous phases used to determine the elastic coefficients are (Pride et al. 2004).

$$K_{m} = (1 - \varphi_{m} )K_{s} /(1 + \tilde{c}_{m} \varphi_{m} ),\quad (m = 1, \, 2).$$

Numerical values of material parameters for the matrix and two distinct porous phases are given in Table 1.

Table 1 Material parameters for the matrix and two distinct porous phases

5.2 Numerical discussion

The aim of the above numerical example is to define the role of various physical properties (like, incident direction, wave frequency, pore characteristics, wave-induced fluid-flow, pore-fluid viscosity and double-porosity structure) on the partition of incident energy among various reflected waves. The distribution of incident energy with incident energy θ₀ ∊ (0, 90°) at the surface z = 0 is shown in Figs. 1, 2, 3, 4, 5 and 6 (for incident P₁ wave) and in Figs. 7, 8, 9, 10, 11 and 12 (for incident SV wave). The detailed discussion on figures is as follows.

Fig. 1

Energy shares of reflected P₁, P₂, P₃ and SV waves and interaction energies (E_IR, E_RR) with incident direction (θ₀) for three different values of embedded porous fraction (ɛ = r/R); $(\omega = 2\pi \,{\text{kHz}},\,\eta = 1\,{\text{m}}{\text{Pa}}\;{\text{s}},\,\xi = 1,\,r = 0.01\;{\text{m}})$; incident P₁ wave

Fig. 2

Energy shares of reflected P₁, P₂, P₃ and SV waves and interaction energies (E_IR, E_RR) with incident direction (θ₀) for three different values of pore-fluid viscosity (η); $(\omega = 2\pi \,{\text{kHz}},\,\varepsilon = 1/3,\,\xi = 1,\,r = 0.01\;{\text{m}})$; incident P₁ wave

Fig. 3

Energy shares of reflected P₁, P₂, P₃ and SV waves and interaction energies (E_IR, E_RR) with incident direction (θ₀) for three different values of embedded sphere size (r); $(\omega = 2\pi \,{\text{kHz}},\,\eta = 1\;{\text{m}}{\text{Pa}}\;{\text{s}},\,\xi = 1,\,\varepsilon = 1/2)$; incident P₁ wave

Fig. 4

Effect of WIFF on the energy shares of reflected P₁, P₂, P₃ and SV waves and interaction energies (E_IR, E_RR) with incident direction (θ₀); $(\omega = 2\pi \;{\text{kHz}},\,\eta = 3\;{\text{m}}{\text{Pa}}\;{\text{s}},\,\xi = 1,\,\varepsilon = 1/2,\,r = 0.001\;{\text{m}})$; incident P₁ wave

Fig. 5

Effect of pore characteristics on the energy shares of reflected P₁, P₂, P₃ and SV waves and interaction energies (E_IR, E_RR) with incident direction (θ₀); $(\omega = 2\pi \,{\text{kHz}},\,\eta = 3\;{\text{m}}{\text{Pa}}\;{\text{s}},\,\varepsilon = 1/2,\,r = 0.001\;{\text{m}})$; incident P₁ wave

Fig. 6

Energy shares of reflected P₁, P₂, P₃ and SV waves and interaction energies (E_IR, E_RR) with incident direction (θ₀) for three different values of wave frequency (ω); $(\eta = 1\;{\text{m}}{\text{Pa}}\;{\text{s}},\,\xi = 1,\,\varepsilon = 1/3,\,r = 0.001\;{\text{m}})$; incident P₁ wave

Fig. 7

Energy shares of reflected P₁, P₂, P₃ and SV waves and interaction energies (E_IR, E_RR) with incident direction (θ₀) for three different values of embedded porous fraction (ɛ = r/R); $(\omega = 2\pi \,{\text{kHz}},\,\eta = 1\;{\text{mPa}}\,{\text{s}},\,\xi = 1,\,r = 0.01\;{\text{m}})$; incident SV wave

Fig. 8

Energy shares of reflected P₁, P₂, P₃ and SV waves and interaction energies (E_IR, E_RR) with incident direction (θ₀) for three different values of pore-fluid viscosity (η); $(\omega = 2\pi \;{\text{kHz}},\,\varepsilon = 1/3,\,\xi = 1,\,r = 0.01\,{\text{m}})$; incident SV wave

Fig. 9

Energy shares of reflected P₁, P₂, P₃ and SV waves and interaction energies (E_IR, E_RR) with incident direction (θ₀) for three different values of embedded sphere size (r); $(\omega = 2\pi \,{\text{kHz}},\,\eta = 1\,{\text{m}}{\text{Pa}}\;{\text{s}},\,\xi = 1,\,\varepsilon = 1/2)$; incident SV wave

Fig. 10

Effect of WIFF on the energy shares of reflected P₁, P₂, P₃ and SV waves and interaction energies (E_IR, E_RR) with incident direction (θ₀); $(\omega = 2\pi \,{\text{kHz}},\,\eta = 3\;{\text{m}}{\text{Pa}}\;{\text{s}},\,\xi = 1,\,\varepsilon = 1/2,\,r = 0.001\,{\text{m}})$; incident SV wave

Fig. 11

Effect of pore characteristics on the energy shares of reflected P₁, P₂, P₃ and SV waves and interaction energies (E_IR, E_RR) with incident direction (θ₀); $(\omega = 2\pi \,{\text{kHz}},\;\eta = 3\;{\text{m}}{\text{Pa}}\;{\text{s}},\,\varepsilon = 1/2,\,r = 0.001\;{\text{m}})$; incident SV wave

Fig. 12

Energy shares of reflected P₁, P₂, P₃ and SV waves and interaction energies (E_IR, E_RR) with incident direction (θ₀) for three different values of wave frequency (ω); $(\eta = 1\;{\text{m}}{\text{Pa}}\;{\text{s}},\,\xi = 1,\,\varepsilon = 1/3,\,r = 0.001\,{\text{m}})$; incident SV wave

5.2.1 Incident P ₁ wave

Figure 1 shows the variation of energy shares with incident direction θ₀ for three different values of embedded porous fraction (ɛ = r/R). It is noted that for θ₀ ∊ (0, 50°), the variational pattern of all the longitudinal waves is alike with respect to ɛ. For θ₀ ∊ (0, 50°), all the longitudinal waves gain some strength with the decrease of ɛ. The effect of ɛ is negligible on the SV wave below 50°. However, beyond 50°, particularly near grazing incidence, the SV wave strengthens with the increase of ɛ. The energy share of the slower P₃ wave is almost negligible in comparison with all the other waves. Near grazing incidence i.e., $\theta_{0} = 90^{ \circ }$ (normal incidence i.e., $\theta_{0} = 0^{ \circ }$ interaction energy E_IR (E_RR) plays a major role in energy conservation. It is clearly visible from the figure that at grazing incidence, most of the incident energy is carried by the SV wave for all the values of ɛ, while at normal incidence, most of the incident energy is carried by P₁ wave. The general observations are that a significant effect of the embedded porous fraction is visible on all the energy shares. The effect of pore-fluid viscosity (η) on the energy shares is shown in Fig. 2. It is observed that the variational patterns of P₁ and P₂ waves are almost alike with respect to η. Near normal and grazing incidences, ɛ, P₁ and P₂ waves are weakened with the increase of η. For incidence below 60°, it increases with the increase in η. A significant impact of η is seen on P₃ wave and interaction energies. The impact of size (r) of an embedded sphere on the variation of energy shares with incident direction θ₀ is exhibited in Fig. 3. For, θ₀ ∊ (0, 60°), almost negligible impact of r is observed on P₁ and SV waves. The P₁ (SV) wave strengthens (weakens) with the increase of r beyond 60°. The behavior of P₁ and P₂ waves is alike with respect to r beyond 60°. The impact of size (r) of the embedded sphere is significant on P₂, P₃ waves and interaction energy E_RR. The variation of energy shares with incident direction θ₀ in the presence and absence of WIFF is shown in Fig. 4. In the presence (absence) of WIFF, the P₁ wave loses some strength (gains some strength) except the range $\theta_{0} \in (20^{ \circ } ,\,60^{ \circ } )$, where the curve corresponding to the presence of WIFF coincides with the curve corresponding to the absence of WIFF. For $\theta_{0} > 78^{ \circ }$, the SV wave strengthens a lot in the presence of WIFF in comparison with the absence of WIFF. The slower P waves are weakened a lot in the presence of WIFF in comparison with the absence of WIFF almost in the whole range of θ₀. Figure 5 displays the effect of pore characteristics (i.e., open pores and closed pores) on the variation of energy shares. Near normal (grazing) incidence, the P₁ wave get stronger (weaker) for closed pores. Beyond 35°, the SV wave strengthens for closed pores in comparison with the open pores. The variational pattern of slower P waves is almost alike irrespective of surface pores being opened or closed. For open pores, slower P₂ and P₃ waves strengthen a lot, particularly for 60° < θ₀ < 90°. Figure 6 exhibits the effect of wave frequency (ω) on the variation of energy shares. It is observed that the energy shares of longitudinal waves are increased with an increase of frequency. A significant impact of frequency is only observed on the SV wave near grazing incidence. The effect of frequency on interaction energy E_RR is very significant in comparison with E_IR.

5.3 Incident SV wave

Figure 7 shows the variation of energy shares with incident direction θ₀ for three different values of embedded porous fraction (ɛ = r/R). It is noted that all the longitudinal waves are strengthened with decrease of ɛ and their variational patterns are almost alike with respect to ɛ. However, very little impact of ɛ is observed on the energy share of the SV wave near grazing incidence. The energy share of the slower P₃ wave is almost negligible in comparison with all the other waves. For $\theta_{0} \in (0,\,\,90^{ \circ } )$, the interaction energy E_RR plays a major role in energy conservation for ɛ = 1/4. The interaction energy E_IR plays a major role in energy conservation near grazing incidence for all values of ɛ. It is clearly visible from the figure that at both normal and grazing incidences the most of incident energy is carried by the SV wave for all the values of ɛ. The effect of pore-fluid viscosity η on the energy shares is shown in Fig. 8. It is observed that the variational pattern of P₁ and P₂ waves is almost alike with respect to η. The P₁ and P₂ waves are weakened with an increase of η for $\theta_{0} \in (0,\,\,90^{ \circ } )$. For incidence below 70°, the SV wave is not sensitive to changes in η while beyond 70°, it decreases with an increase in η. A significant impact of η is seen on the P₃ wave and interaction energies, particularly on E_RR. The impact of size (r) of the embedded sphere on the variation of energy shares with incident direction θ₀ is exhibited in Fig. 9. For $\theta_{0} \in (0,\,\,60^{ \circ } )$, almost negligible impact of r is observed on P₁ and SV waves. The P₁ and SV waves are weakened with the increase of r beyond 60°. The impact of size (r) of the embedded sphere is significant on P₂, P₃ waves and interaction energies. The variation of energy shares with incident direction θ₀ in the presence and absence of WIFF is shown in Fig. 10. It is observed that for P₁ and SV waves, the curve corresponds to the presence of WIFF for θ₀ < 45°. The P₁ and SV waves are weakened a lot in the presence of WIFF in comparison with the absence of WIFF beyond 45°. The slower P waves are weakened a lot in the presence of WIFF in comparison with the absence of WIFF in almost the whole range of θ₀. Figure 11 displays the effect of pore characteristics (i.e., open pores and close pores) on the variation of energy shares with incident direction θ₀. Near normal and grazing incidences, the impact of pore characteristics is not observed on both P₁ and SV waves. It is observed that for fully closed surface pores, the P₁ (SV) wave becomes stronger in the range 15° < θ₀ < 40° (45° < θ₀ < 85°). The variational pattern of slower p waves is almost alike irrespective of surface pores being opened or closed. For fully opened surface pores, slower P₂ and P₃ waves are strengthened a lot. Figure 12 exhibits the effect of wave frequency (ω) on the variation of energy shares. It is observed that the energy shares of longitudinal waves increases with the increase of frequency. The effect of frequency on the SV wave is observed near grazing incidence only. The effect of frequency on interaction energy E_RR is much significant in comparison with E_IR.

6 Conclusions

In this article, reflection of attenuated waves at the stress-free surface of double-porosity dual-permeability materials is investigated. A double-porosity dual-permeability material is considered dissipative due to the presence of viscosity in the pore fluid. Therefore, all the waves (i.e., incident and reflected) are attenuated (i.e., different directions of propagation and attenuation) in nature due to the dissipative nature of the medium. The energy shares of reflected waves are computed analytically and numerically for the incidence of two main waves (i.e., P₁ and SV) at the interface z = 0. Due to the dissipative nature of the medium, the conservation of incident energy at the interface z = 0 is confirmed by considering the interaction energy between two dissimilar waves. Finally, for particular numerical examples, the effect of various physical properties (like, incident direction, wave frequency, pore characteristics, wave-induced fluid-flow, pore-fluid viscosity and double-porosity structure) on the partition of incident energy among various reflected waves is studied. The present study plays an important role in reservoir engineering where reservoir engineers use the reflection method to distinguish these fluids and to understand their flow characteristics. Some conclusions are addressed which may be drawn from the discussions of the numerical results.

• All the energy shares are strongly associated with incident direction, wave frequency, pore characteristics, wave-induced fluid-flow, pore-fluid viscosity and double-porosity structure for both incidences.

• At the normal (grazing) incidence of P₁ wave, the major part of incident energy is carried by the P₁ (SV) wave. While at both normal and grazing incidence of the SV wave, the major part of incident energy is carried by the SV wave only.

• All the longitudinal waves are strengthened with the increase of wave frequency for both incidences, i.e., P₁ and SV waves.

• For both incidences, P₂ and P₃ waves are weakened in the presence of WIFF.

• For both incidences, the variation pattern of slower P waves is almost alike irrespective of surface pores being fully closed or fully opened.

• Near grazing incidences of P₁ wave, the slower P waves are strengthened a lot irrespective of fully opened surface pores.

• In mathematical framework, it has been confirmed from the numerical interpretation that during reflection process, conservation of incident energy is obtained at each angle of incidence.