Abstract
It is of real and direct significance for China to cope with oil price fluctuations and ensure oil security. This paper aims to quantitatively analyze the specific contribution ratios of the complex factors influencing international crude oil prices and to establish crude oil price models to forecast long-term international crude oil prices. Six explanatory influential variables, namely Dow Jones Indexes, the Organization for Economic Cooperation and Development oil stocks, US rotary rig count, US dollar index, total open interest, which is the total number of outstanding contracts that are held by market participants at the end of each day, and geopolitical instability are specified, and the samples, from January 1990 to August 2017, are divided into six sub-periods. Moreover, the co-integration relationship among variables shows that the contribution ratios of all the variables influencing Brent crude oil prices are in accordance with the corresponding qualitative analysis. Furthermore, from September 2017 to December 2022 outside of the sample, the Vector Autoregressive forecasts show that annually averaged Brent crude oil prices for 2017–2022 would be $53.0, $61.3, $74.4, $90.0, $105.5, and $120.7 per barrel, respectively. The Vector Error Correction forecasts show that annual average Brent crude oil prices for 2017–2022 would be $53.0, $56.5, $58.5, $60.7, $63.0 and $65.4 per barrel, respectively.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Petroleum is the pillar of the bulk commodities. In addition to its basic commodity attributes, petroleum has strong special financial and political attributes. In past decades, international crude oil prices experienced significant ups and downs and attracted extensive attention across the academic and industrial communities (Wu and Zhang 2014). The drastic fluctuations of international crude oil prices could have played an important role in national economic power (Han et al. 2017; Yao et al. 2017; Timilsina 2015; Yu et al. 2015; Wang and Zhang 2014; Zhang 2011; Wei et al. 2008; Jiang and Jiang 2005), inflation and unemployment (Du et al. 2010; Uri 1996), stock markets (Cong et al. 2008), fundamental industries (Jiao et al. 2012), financial markets (Zhang 2013; Zhang and Wang 2013), political situation, military strength (Jianwei et al. 2017) and national security (An et al. 2014). Moreover, with the rapid development of China’s economy, it has become the second largest oil consumer and the third highest oil-importing country in the world. Its dependence on imported oil exceeds 65% (Wu and Zhang 2014). Therefore, it is necessary to make a comprehensive and systematic review and qualitative and quantitative analysis of all factors affecting the international oil price fluctuation and to forecast crude oil price as accurately as possible. It is of real and direct significance for the China Petroleum and Chemical Corporation (Sinopec) to be able to cope with the fluctuation of international crude oil prices and to ensure oil security and procurement.
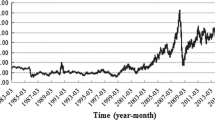
As shown in Fig. 1, in August 1990, due to the Iraqi invasion of Kuwait, the United Nations put a total embargo of oil exports from Iraq and Kuwait. The outbreak of Gulf War and the United Nations embargo led directly to a reduction in crude oil supply by 4.7 million barrels/day in the international oil market, which was 7% of the global aggregate demand at that time (Yan 2012). Following this, the international Brent oil price rose from $19.59 per barrel in February 1990 to $35.03 per barrel in October 1990. However, thanks to the timely increased production in OPEC countries, the supply shortage of 3 million barrels per day in this oil crisis was quickly supplemented. So, compared with the previous two crises, the fluctuation of international oil price brought by this oil crisis didn’t last too long and didn’t have a substantial impact on the world economy. After this crisis, oil prices fell back to the low level of before the war, i.e., $19.22 per barrel. From 1997 to 1998, the strong impact of the Asian financial crisis on world economy (according to IMF, the economic growth in 1998 was only 2.8%) and oil demand in 1997, the international Brent oil price dropped continuously and fell to $10 per barrel, historically low levels, in December 1998. Afterward, due to the three times underproduction implemented by OPEC, the international oil price quickly rose to around $25 per barrel at the end of the year 1999. Throughout 1990s, oil prices fluctuated smoothly, which basically maintained the range from $10.19 per barrel to $35.03 per barrel.
In the 21st century, there were some new features in the international crude oil market, including the increasing globalization of the oil market, the rapid growth of oil demand in non-OECD countries and the strengthening in the financial attributes of petroleum. The international crude oil prices showed large fluctuations and upward shocks. They fell from $25.22 per barrel in January 2000 to $19.06 per barrel in December 2001 due to the weakening of the US and global economies and the slowdown in oil demand caused by the “911” attacks and then continually went up to $32.18 per barrel in February 2003, the eve of the outbreak of the Iraq war. From 2000 to 2004, the economic resurgence brought a rapid increase in crude oil demand. Oil demand in OECD and Asia rose by 0.6% and 4.8% annually, respectively (IEA). Since 2005, the oil prices gradually entered into a high-level stage and increased to a record high in July 2008, i.e., $134.56 per barrel. Not only the Iraq war, Venezuela and Nigeria strikes and the hurricanes (Ivan, Katrina and Rita), but also the rapid growth in the global economy, the tight supply–demand balance, high spirits in speculations from other finance and commodity trading markets into oil market and the devaluation of US dollar caused by the reduction of interest rates of Fed pushed up oil prices. Afterward, because of the global financial crisis, world oil demand was slashed and oil price dramatically slumped toward about $43.05 per barrel in December 2008. Since February 2009, however, the oil price has experienced short-term low-level fluctuations and then rebounded continuously. In February 2011, oil price exceeded $100 per barrel again in just five months, i.e., $104.03 per barrel. From January 2011 to June 2014, the oil price remained volatile at a high level with a slight upward trend (Wu and Zhang 2014). However, high oil prices led to a significant increase in shale oil production in the USA. The transition from tight supply–demand to loose supply–demand dominated the international oil prices, which basically fluctuated within the range of $95–$130 per barrel. From the second half of 2014, oil production in USA had been growing rapidly, driven by the breakthrough in shale oil technology and the repeal of the 40-year-old US oil export embargo in December 8, 2015. In addition, the substantial growth in OPEC oil supply, weak oil demand, stronger US dollars and the increase in speculation caused oil prices to descend again to $31.93 per barrel in January 2016. Subsequently, oil prices have been slowly shored up above $50 per barrel because OPEC and non-OPEC producers reached an agreement on production reductions for the first time in November 30 and December 8, 2016, respectively.
Some scholars believe the international oil price depends mainly on the supply and demand balance (Bunn et al. 2017; Mi et al. 2017; Zhang et al. 2015, 2017). Based on the above detailed reviews of the historical international oil market and oil price, it is demonstrated that the determinants influencing oil price fluctuations at different stages are not only the fundamental factors of supply and demand like other bulk commodities, but also many other invisible and complex factors such as the influence of dollar exchange rate fluctuation, opportunistic practices in the futures market, geopolitical instability and emergencies, the security of the oil traffic path (Zhang and Yao 2016; Zhang and Zhang 2015). Therefore, which factors play a leading role in the fluctuation of international oil prices at different stages and what are the relative contributions of the main factors? And how will the international oil market and the trend of international oil prices develop in the future? It is hoped that the answers to the above questions will be helpful for the relevant oil investors to analyze and forecast international crude oil prices, and for policy makers to monitor and regulate the crude oil market.
To accommodate the multitude of factors that potentially determine oil prices, six groups of full explanatory factors in this study can be classified as possible contributors to the development of crude oil prices: Economics, Fundamentals, Technology, Finance, Speculation and Geopolitics. And all the influential factor groups don’t necessarily contradict, but rather may complement one another. This paper attempts to divide the whole fluctuation range of international crude oil prices from January 1990 to August 2017 into several sub-periods and examine different variables relating to each of these six groups. Furthermore, we investigated the long-term relationship between international crude oil prices and selected determinants by using co-integration theory to quantitatively analyze the contribution of different factors to international crude oil prices at different stages. Then, we examined whether the empirical results are in accordance with the corresponding qualitative characteristics of the historical oil market and the fluctuation of oil prices. Subsequently, we established the oil price forecast models, VAR (Vector Autoregressive) model and VEC (Vector Error Correction) model, to make predictions of international oil prices from January 1990 to August 2017 inside of the sample and from September 2017 to December 2022 outside of the sample.
The remainder of this paper is organized as follows. Section 2 proposes the related literature review, and Sect. 3 describes the data definitions and econometric methodologies, namely VAR and VEC models. Section 4 provides the empirical results and analyses, and Sect. 5 puts forward main conclusions as well as policy implications.
2 Literature review
It is hardly surprising that oil price determinants have become a popular area of research. Some previous studies have already looked at the interacting relationships between international crude oil prices and the factors influencing them. On the Economic factor side, the fall in oil prices has positive real output effects for the global economy and lower oil prices have been good for the US economy since the 2008 financial crisis (Mohaddes and Pesaran 2017; Ratti and Vespignani 2016). On the Fundamental factor side, a change in market structure could have contributed to OPEC exercising its market power, and demand response to crude oil prices has almost doubled during the crisis (Genc 2017). On the Oil Exploration Technology factor side, the US total oil rigs and total gas rigs variables provide an approximate indication of the current level of US production. Most notably, the number of US oil rigs has increased significantly over the last ten years, while the rise in the number of gas rigs has been less pronounced (Breitenfellner et al. 2009). On the Financial factor side, the relationship between oil price shocks and the bilateral exchange rate of the US dollar against currencies in 16 OECD countries was investigated (Chen et al. 2016a, b). Empirical results show evidence of a long-run equilibrium relationship between oil price and exchange rate, especially for currencies of the key oil-exporting countries (Mensah et al. 2017). On the Speculation factor side, it is demonstrated that the impact mechanisms of investor attention have significant negative impacts on oil prices during 2004–2016 and contributes 15% to the long-run fluctuation of oil prices (Yao et al. 2017). The instantaneous feedback of speculators on crude oil price proves significant. The speculators’ impact on oil price has strong linearity but weak nonlinearity. The linear influence is symmetric when oil price goes up or down. When the oil price is highly volatile, speculation has a clear linear impact on it (Zhang 2013). On the Geopolitical Instability factor side, when analyzing the impacts of China’s oil imports on international oil prices, the unexplained fluctuations of oil prices may result from the geopolitical events. (Wu and Zhang 2014). However, geopolitical indicators are not easy to quantify. The present studies mainly adopted qualitative methods to describe the impacts of political events on oil price fluctuation, and comparatively fewer studies have quantitatively estimated the impact of political instability on the oil prices. The first quantitative assessment of the influence of political event on oil prices may have originated from the publications about OPEC and world crude oil markets from 1973 to 1994 (Coleman 2012; Alhajji and Huettner 2000). The previous quantitative researches can be divided into three categories (Chen et al. 2016a, b). One of the three categories is that the occurrence time of the political events as the basis for division of the study period and the breakpoints are often regarded as 0–1 dummy variables. In 2000–2015, this category was applied at the time point of major oil events (Zhou 2016). In addition to the research into a single influential factor of international crude oil prices, some scholars have investigated the comprehensive indicators affecting the oil prices (Miao et al. 2017; Wang and Sun 2017; Zhu et al. 2015; Yan 2012; Breitenfellner et al. 2009). Nevertheless, according to the historical features of international oil market and oil prices of each sub-period, the present research does not quantitatively analyze the specific contribution of the various influential factors to international crude oil prices, which is one innovative aspect in this paper.
Considering the econometric methodologies of investigating the relationship among international crude oil prices and their influencing variables, VAR and VEC models have been widely used. The transmission and feedback mechanisms between international crude oil prices and China’s refined oil prices for the time span from January 2011 to November 2015 are based on VAR and VEC models (Han et al. 2017). An empirical study on the relationship between prices of crude oil and retail refined oil based on VAR model is currently unavailable (Jiang 2013). However, VAR and VEC models have been less applied to statistically forecast long-term international crude oil prices in current literature. This is another innovative aspect of this paper.
3 Data and econometric methodology
3.1 Variable combination selection and data specifications
International Brent crude oil covers 80% of the world crude oil trading volume. The Brent price is specified as a proxy for the international crude oil price level. Understanding the factors driving crude oil price development is essential for assessing their effects. In order to pick out the appropriate influential variables, this paper examines a total of some 25 potential variables relating to each of the six groups previously outlined (Economics, Fundamentals, Technology, Financial factors, Speculation and Geopolitical instability). Table 1 presents the set of variables and detailed descriptions which are used as potential covariates. The variables are measured at monthly frequency, and they represent different oil supply and demand factors, as well as factors related to financial markets and the structure of the market for oil. Then, the criteria of variable selection are as follows: (1) Examine the correlation coefficients on the international crude oil prices and each individual indicator of the six groups to determine if they are economically significant. The variable satisfying this condition and with the largest correlation coefficient in each factor group is the proxy for each influential factor group of international Brent crude oil prices. (2) According to the fluctuation characteristics of the international oil market and Brent oil prices previously reviewed, compared with the previous two crises before 1990, the ability of OPEC to resist oil disruptions and soaring oil prices has improved substantially. Thus, the research scope starts from the outbreak of Gulf War in January 1990 to August 2017. The data availability of individual indicators is one of the criteria of variable selection.
The results in Table 1 show that in the economic factor group, all of the examined variables satisfy the first criterion. But considering the second criterion, DJI, the most representative barometer of the American economy and worldwide mature stock market, is the most appropriate. In the fundamental market factor group, non-OECD oil demand, worldwide oil demand, OECD oil stocks and OPEC surplus oil production capacity have economic significance on the international Brent crude oil prices. OECD oil stocks is the most appropriate factor, because in some sense, the difference between oil supply and oil demand has reflected the change in oil stocks and these two types, which represent the fundamental variables, cannot be used simultaneously. Besides, compared to OPEC surplus oil production capacity, OECD oil stocks are more negatively related to the Brent oil prices. In the oil exploration technology group, we select the US rotary rig count, highly positively related to Brent oil prices. In the financial market factor group, US dollar index (USD), as an aggregative indicator of the weighted average value of six major currencies against US dollars, reflects the exchange rate of US dollars in the international foreign exchange market and measures the exchange rate of the US dollars against a basket of currencies. USD has a strong negative correlation coefficient on Brent oil prices. In oil exploration technology, we select the US rotary oil rig count as a proxy. In the speculation factor group, the net positions of Large traders, Managed money and Small traders have economic significance for Brent oil prices. TOI, however, has a more positive relationship on Brent oil prices. Important geopolitical and historical events (e.g., the Second Gulf War from August 1990 to April 1991 and the Iraq War in 2002) are also accounted for by using 0–1 dummy variables.
In addition to the explained variable, international Brent oil prices, six explanatory variables are eventually specified for each influential factor groups: DJI, OECD oil stocks, US rotary rig count, US dollar index, TOI, Geopolitical instability, which are quoted as pbrent, dji, oeoi, rig, usdx, toi, gpo. Since variable units are not uniform, normalized units of pbrent, oeoi and toi are USD/barrel, barrel and barrel, respectively. The diagrams in Fig. 2 illustrate the relationship between these six influential variables and international Brent crude oil prices. All data are on a monthly basis and are transformed into logarithmic values before further investigation, which does not change the original co-integration relation between variables (Sun 2013) and can linearize the trends and eliminate the heteroscedasticity in the time series. The logarithmic variables are denoted as lpbrent, ldji, loeoi, lrig, lusdx, ltoi and gpo, respectively.
The whole sample, January 1990 to August 2017, is divided into the six sub-periods January 1990 to December 1996, January 1997 to December 2002, January 2003 to December 2006, January 2007 to December 2008, January 2009 to June 2014 and July 2014 to August 2017. The breakdown by decades is useful in that it proxies phases of key international Brent oil prices development: The Asian financial crisis in 1997; the outbreak of the Iraq war in 2003; the tight supply–demand, the devaluation of US dollar and high spirits in speculations from 2007 to the outbreak of the global financial crisis in 2008; the oil price boom in 2009 after the global financial crisis until volatility on a high level with a slight upward trend from 2011 to June 2014; oil price descent again after June 2014 and a slight upwards from January 2016 to August 2017.
3.2 VAR and VEC models based on co-integration theory
3.2.1 Co-integration theory
The co-integration method studied by Engle and Granger (Ford and Dickinson 2010) facilitates the analysis of non-stationary time series. If the linear combination of these non-stationary variables can form a stationary time series, the resulting linear combination is called a co-integration equation, which means these variables exhibit a co-integration relationship.
In this paper, the Johansen multivariate co-integration test method (Engle and Granger 1987; Bondia et al. 2016; Ouyang and Lin 2015; Johansen 1988; Johansen and Juselius 1990; Moore and Copeland 1995) is used to carry out the co-integration test. The Johansen co-integration test is based on VAR. The original time series variables must be guaranteed to be in the same order sequence. The basic principle of the Johansen co-integration test is to analyze the rank of the matrix \(\varPi\) in Eq. (1).
If the rank of \(\varPi\) is equal to \(n\), \(y_{t}\) is a stationary variable. If the rank of \(\varPi\) is equal to 0, there is no long-run co-integration relationship existing between the variables. If the rank of \(\varPi\) in the range of 0~n, there are r long-term co-integration relationships existing between the variables.
The Johansen co-integration test has two test statistics: the trace test statistic \(\mathop \lambda \nolimits_{\text{trace}}\) and the maximum eigenvalue test statistic \(\mathop \lambda \nolimits_{\hbox{max} }\), which are shown in Eq. (4) and Eq. (5).
3.2.2 VAR and VEC models
VAR and VEC models are commonly used in systems forecasting interrelated time series and analyzing the dynamic impact of random disturbances on a system of variables (Ghysels 2016; Park et al. 2011).
VAR is an unstructured model, which means the relationship between variables is not based on economic theory. VAR constructs the model by treating every endogenous variable in the system as a function of lagged values of all of the endogenous variables in the system. The most general mathematical expression of VAR is:
where \(y_{t}\) is a \(k\)-dimensional vector of endogenous variables; \(y_{t - i} = \left( {i = 0,1, \ldots ,p} \right)\) is a lagged endogenous variable vector; \(x_{t - i} = \left( {i = 0,1, \ldots ,r} \right)\) is a \(d\)-dimensional vector of exogenous variables or a vector of lagged exogenous variables; \(P,r\) are the lag order of endogenous variables and an exogenous variables; \(k \times k\) dimensional matrix \(A_{t}\) and \(k \times d\) dimensional matrix \(B_{i}\) are the coefficient matrices to be estimated. \(\varepsilon_{t}\) is a \(k\)-dimensional random disturbance vector.
VEC is actually a vector autoregressive model with co-integration constraints on the basis of time series variables and only applicable to modeling of non-stationary time series variables with long-term co-integration relations. The first-order difference time series variables obtained by the error correction method are almost orthogonal, which can eliminate the multiple collinearity between the time series variables and improve the explanatory strength of model equations. If \(k\) variables of \(I(1)\) have a co-integration relationship in \(y_{t}\), Eq. (6) without exogenous variables can be written as Eqs. (7) and (8):
where \({\text{ECM}}_{t - 1}\) is an error correction term. Each equation in Eq. (8) is an error correction model. The error correction term reflects the long-run equilibrium relations among the variables (co-integration relationship), which means deviations from the long-run equilibrium can be corrected by a series of partial short-term adjustments. \(\alpha\) is the coefficient vector of the error correction term and represents the adjustment speed to the long-term equilibrium state, when the balanced relationship between variables deviates from the long-term equilibrium. \(\varGamma {}_{i}\) is the coefficient of the lag difference term \(\Delta y_{t - i}\) of each explanatory variable and reflects the effects of short-term fluctuations of each variable on \(\Delta y_{t}\).
Without imposing theoretical restrictions on endogeneity among variables, VAR and VEC models can be appropriate to establish the dynamics between the international Brent crude oil prices and all the influential variables. The quantitative analysis software, Eviews6.0, is used in this study to carry out the analysis.
4 Empirical analysis and forecast
4.1 Contributions of influential factors to Brent oil price
4.1.1 Optimal lag order determination
First of all, it is necessary to conduct the optimal lag order analysis, which can reduce and eliminate the autocorrelation between variables in residuals and reflect the dynamic characteristics of the model (Ng and Perron 2001). However, the longer the optimal lag order is, the more the value of the parameter to be estimated and the less the freedom in the model. This will directly affect the validity of the model estimation. When the optimal lag order is too small, residual autocorrelation problems may be present, which can result in inconsistencies of parameter estimation. So, it is necessary to balance between the optimal lag order and freedom.
To analyze the optimal lag order, there are five evaluation criteria, namely Likelihood Ratio (LR), Final Prediction Error (FPE), Akaike Information Criterion (AIC), Schwarz Information Criterion (SC) (Pedroni 2008) and Hannan–Quinn Information Criterion (HQ). Taking the third sub-period in January 2003 to December 2006 as an example, results for the lag order are given in Table 2, which shows that the lag order selected by the 3 criteria LR, SC and HQ is 1. The optimal lag order analysis of other five sub-periods is the same as that of the first sub-period. Ultimately, the optimal lag order of each sub-period is 2, 2, 1, 1, 1 and 2, respectively.
4.1.2 ADF unit root test for stationary tests
Because of the spurious regression problems, non-stationary variables should not be directly used in the regression model. Otherwise, the direct use of non-stationary variables for regression analysis leads to a high output value and a very significant t value, but the estimation and analysis of the model doesn’t have any substantive significance (Granger and Newbold 1974). It is necessary to implement a stationary test, namely the unit root test, before establishing VAR and VEC models (Xu and Lin 2016; Blanco et al. 2013). The Augmented Dickey–Fuller (ADF) of the unit root test method is commonly applied to check sequence stationary (Dickey and Fuller 1979; Jansson and Nielsen 2012; Gavaliere 2014). The test models of the ADF unit root test method are as follows.
where \(\varepsilon_{t}\) is a random disturbance term; \(\Delta\) is a differential operator. Equation (9) represents the model with no intercept and no trend. Equation (10) represents the model with intercept and no trend. Equation (11) represents the model with intercept and trend. The specific test starts with Eq. (11), then Eqs. (10) and (9). Only when the final test is done, we can know whether the original time series has a unit root. Table 3 provides the results of the ADF unit root tests for the time series of the third sub-period in January 2003 to December 2006. It can be found that the ADF unit root test statistics of these seven variables are greater than 1%, 5% and 10% test critical values. That is, the null hypothesis of a unit root cannot be rejected at the 1%, 5% and 10% significance level, which means all the variables are non-stationary sequence. Then, the stationary test of all the variables in the first-order difference is conducted. The ADF unit root tests indicate that the test statistics of these seven variables are lower than 1%, 5% and 10% critical values. That is, the null hypothesis of a unit root in the first-order difference can be rejected for all the variables at the 1%, 5% and 10% significance level, which means all the variables form a stationary sequence.
After the ADF unit root test for all the variables in the whole sub-periods, it can be concluded that all the variables are stationary in the first-order difference and can be conducted with a co-integration test.
4.1.3 Johansen co-integration test
The Johansen co-integration test method previously introduced in Sect. 3.2.1 is used to carry out the co-integration test to examine whether there is a long-term stable relationship between variables (Engle and Granger 1987; Bondia et al. 2016; Ouyang and Lin 2015; Johansen 1988; Johansen and Juselius 1990; Moore and Copeland 1995). According to the co-integration theory Eqs. (1)–(3), the results are shown in Table 4. The trace statistic of “no co-integration relationship” is equal to 143.77, which is greater than the 0.05 critical value, so it can reject the original hypothesis \(H_{0}\) that there is no co-integration relationship. The trace statistic of “at most one co-integration relationship” equals to 90.99, which is smaller than the corresponding 0.05 critical value, so it cannot reject the alternative hypothesis \(H_{1}\) that there is one co-integration relationship. The Max-Eigen statistic of “no co-integration relationship” and “at most one co-integration relationship” is equal to 52.77 and 41.21, respectively, which are greater than the 0.05 critical value, so it can reject the original hypothesis \(H_{0}\) and the alternative hypothesis \(H_{1}\). The Max-Eigen statistic of “at most two co-integration relationship” is equal to 24.97, which is smaller than the corresponding 0.05 critical value, so it cannot reject the alternative hypothesis \(H_{2}\). In other words, there is at least one long-term stable equilibrium relationship between international Brent crude oil prices and influential variables at the 0.05 level. After the Johansen co-integration tests for all the variables of the whole sub-periods, it can be concluded that there is one long-term stable equilibrium relationship between the international Brent crude oil prices and influential variables at the 0.05 level.
Inverse roots of the AR characteristic polynomial of the co-integration relationship are shown in Fig. 3. The VAR stability condition check is shown in Table 5. It can be seen that no root lies outside the unit circle and VAR (1) satisfies the stability condition.
The co-integration relationship of the third sub-period from January 2003 to December 2006 is shown in Table 6.
According the Table 6, the long-term co-integration equation between the international Brent crude oil prices and influential variables is shown in Eq. (12).
From Eq. (12), it can be seen that the elasticity coefficients of the impacts of lpbrent, ldji, loeoi, lrig, lusdx, ltoi and gpo on lpbrent are 10.77, − 2.90, − 1.79, − 0.49, 5.59 and 0.35, respectively. Thus, the contribution ratios of the six explanatory variables to the explained variable lpbrent are 49.2%, 13.3%, 8.2%, 2.2%, 25.5% and 1.6%, respectively.
On the whole, the long-term co-integration relationships between the international Brent crude oil prices and all the influential variables of each sub-period can be calculated as follows from Eqs. (13)–(17).
4.1.4 Comprehensive quantitative and qualitative analysis
From Eqs. (12)–(17), in terms of the co-integration relationships between international Brent crude oil prices and all the influential variables of each sub-period, the comprehensive contribution ratios can be eventually calculated in Table 7. Besides, the results in Table 7 can be graphed in Fig. 4 for comprehensively quantitative and qualitative analysis. Then, from the perspective of the whole sub-periods and all the influential variables, examine whether the quantitative results are in accordance with the corresponding qualitative characteristics of historical oil market and the fluctuation of oil prices.
-
(1)
From the perspective of all the whole sub-periods. In the first sub-period from January 1990 to December 1996, after the outbreak of Gulf War in 1990, the first comprehensive international energy cooperation was conducted. In addition to Iran, OPEC agreed to increase their oil production in order to make up for the supply shortage in the international oil market due to the embargo of the United Nations on Iraq. Thus, the fundamental factor plays a leading role in the fluctuations of international crude oil prices. The contribution ratio of loeoi is above 50.0%. In the second sub-period from January 1997 to December 2002, after the strong impact of the Asian financial crisis on the world economy and oil demand, OPEC conducted a reduction of output three times. The fundamental factor remained the strong role in leading oil price fluctuations. The contribution ratio of loeoi is 48.2%. In the third sub-period from January 2003 to December 2006, the effect of loeoi, the proxy of fundamental factor group, on the international Brent oil prices diminished to 13.3%. The rapid growth in the global economy, the devaluation of the US dollar and high spirits of speculators in the crude oil market are the main drivers pushing up the international Brent crude oil prices. The effects of ldji and ltoi, the proxies of the economic factor group and speculation factor group, account for 49.2% and 25.5%, respectively. In the fourth sub-period from January 2007 to December 2008, after the global financial crisis, the international Brent crude oil prices dropped mainly because of the declines in oil demand and speculations and the stronger US dollar. The main influential factors affecting the fluctuations of Brent crude oil prices returned from the speculations to the fundamental factor. The effects of loeoi, ldji and ltoi account for 32.3%, 39.1% and 13.5%, respectively. In the fifth sub-period from January 2009 to June 2014, the economic factor, the fundamental factor and geopolitical instability are the main influential factors of Brent crude oil prices, which account for 18.5%, 44.1% and 4.6%. In the sixth sub-period from July 2014 to August 2017, oil production in US had been growing rapidly, driven by the breakthrough in shale oil technology and the cessation of the 40-year oil-exporting embargo in December 8, 2015. Iran oil exports lifted in January 16, 2016. Many factors work together on oil prices. The loeoi, lrig, lusdx and ltoi account for 22.1%, 10.0%, 29.6% and 22.1%.
-
(2)
From the perspective of all the influential variables. From all the influential variables, overall, loeoi, the proxy of the fundamental factor, has a major effect on international Brent crude oil prices. ldji mainly reflects impacts of the stock market, market expectations and economic factors on crude oil prices. The greater impacts in 2003–2006 are attributable to the expansion in supply and demand and to the economy. lrig reflects the oil exploration and development techniques, with greater impacts in 2009–2017. lusdx reflects the impacts of asset pricing on oil prices, with greater impacts in 2007–2008 and 2014–2017, which mainly because rapid devaluation and revaluation of the US dollar pushed up the international Brent crude oil price. The more significant period of ltoi spans in 2003–2006 because the relaxation of capital regulations in 2003 permitted banks to participate in investment banking and commodity trading.
The overall quantitative analysis results show that the impacts of all the influential variables at the whole sub-periods on the international Brent crude oil prices are consistent with the qualitative analysis results of the characteristics of the fluctuations of international crude oil markets and Brent crude oil prices. This illustrates that the co-integration relationships between international Brent crude oil prices and all the influential variables at each sub-periods have strong explanatory power.
4.2 Forecasts for Brent oil prices inside and outside of the sample
After a quantitative analysis of the contribution ratios of each influential explanatory variable on the international Brent crude oil prices, we established the oil price forecast VAR and VEC models in the whole sample from January 1990 to August 2017. Similarly, we determined the optimal lag order. The test results show that the optimal lag order is 2. Secondly, the ADF unit root test is used to examine if each variable is stationary. The test results indicate that the original time series of all the influential variables, namely lpbrent, ldji, loeoi, lrig, lusdx, ltoi and gpo, are unstable, while the first-order difference time series of each variable are stable. It can be concluded that all the variables are stationary in the first-order difference and can be conducted with a co-integration test. Thirdly, the Johansen co-integration test is used to determine the co-integration relationships between the international Brent crude oil prices and all the influential variables. The test results that the trace statistic and the Max-Eigen statistic of the original hypothesis “no co-integration relationship” are greater than the 0.05 critical value. The trace statistic and the Max-Eigen statistic of the alternative hypothesis “at most one co-integration relationship” are less than the 0.05 critical value. This indicates there is a long-term stable co-integration equilibrium relationship between international Brent crude oil prices and all the influential variables at the 5% significant level. All of the inverse roots of AR characteristic polynomials are located within the unit circle. The VAR(2) satisfies the stability condition. VAR and VEC models can be further established to make forecasts of Brent oil prices from January 1990 to August 2017 inside of the sample and from September 2017 to December 2022 outside of the sample. Combined with the future international oil market situation, we compared the forecast effects of VAR and VEC models.
4.2.1 Establishment of oil price forecast model VAR
According to Eq. (6), we established the VAR (2) of all the influential variables lpbrent, ldji, loeoi, lrig, lusdx, ltoi and gpo. According to the parameter estimation results of VAR model, the specific form is shown in Eq. (18).
The results of VAR estimates and model diagnostic tests are shown in Table 8. The VAR are fitted well, and the overall effect of the model is good.
4.2.2 Establishment of oil price forecast model VEC
According to Eqs. (7) and (8), establish the VEC (1) model of all the influential variables lpbrent, ldji, loeoi, lrig, lusdx, ltoi and gpo. According to the parameter estimation results of VEC model, the specific form is shown in Eq. (19).
where
The results of VEC estimates and model diagnostic tests are shown in Table 9. The overall fitting effect of the VEC model is not superior to VAR.
4.2.3 Brent crude oil price forecasts for 1990–2017 inside of the sample
With the dynamic solution and static solution, we used the above VAR and VEC models to forecast the international Brent crude oil prices from January 1990 to August 2017 inside the sample. The dynamic solution uses the predictive value of each sequence rather than actual observation to iteratively calculate and can forecast the future variables outside of the sample. Although it can’t show short-term fluctuations in prices, it can reflect the price trends better. Thus, it is suited to long-term forecasts. The static solution uses the actual observation value of the lag period of each sequence to determine the next forecast value. However, it can only predict the future values of one period outside of the sample. This solution can better show short-term fluctuations than long-term trends of prices. Thus, it is suited to short-term forecasts. For dynamic solution and static solution of VAR and VEC models, a set of sequences containing the original sequence lpbrent and the analog sequence lpbrent (Baseline) can be established, which are shown in Fig. 5. It can be seen that compared to the dynamic solution, the static solution results of VAR and VEC models are closer to the actual international Brent crude oil prices. For the static solution results inside of the sample, the absolute error of VEC is a slight larger than that of VAR. The forecast effect of VAR is better than VEC.
4.2.4 Brent crude oil price forecasts for 2017–2022 outside of the sample
In order to ensure the accuracy of the model prediction, the static solution of VAR and VEC is applied to predict the monthly international Brent crude oil prices from September 2017 to December 2022 outside of the sample. The forecast results are shown in Fig. 6. It can be seen that the forecast results of VAR show that annually averaged Brent crude oil prices outside of the sample from 2017 to 2022 are $53.0, $61.3, $74.4, $90.0, $105.5, and $120.7 per barrel, respectively. The forecast results of VEC show that annually average Brent crude oil prices outside of the sample from 2017 to 2022 are $53.0, $56.5, $58.5, $60.7, $63.0 and $65.4 per barrel, respectively.
The latest report IEA Market Report Series: Oil 2017 provides clear trends to guide our view about the oil market of the next five years. The Oil 2017 report, which provides market analysis and forecasts to 2022, sets the scene for what promises to be a transformative period in the history of oil. The downturn in investment will lead to a worldwide supply shortage of crude oil after 2020. (1) Oil demand is expected to grow strongly at least to 2022 with the main developing economies leading the way. (2) The need for more production capacity becomes apparent by the end of the decade, even if supply appears plentiful today. (3) It is not clear that upstream projects will be completed in time given the unprecedented two-year fall in investment in 2015 and 2016 although major reductions in costs will help. (4) There is a risk of prices rising more sharply by 2022 if the spare production cushion is eroded. The global oil market is likely to fall into a quagmire of supply shortages.
From the point of view of IEA, obviously, the fundamental factor is still a big driver influencing the fluctuations of international Brent crude oil prices. Two scenarios can be set up to analyze the development of oil prices: low development scenario and high development scenario. The high reservoir development scenario means that if new oil projects are to be launched, worries about low reserve oil production capacity will be eased, and the crude oil futures curve will be more resilient. Thus, the international Brent crude oil prices will slowly rise along the forecast results of VEC. The low reservoir development scenario means that if new oil projects continue to be blocked, the reserve crude oil production capacity will further reduce. Thus, the increased fluctuations of oil prices will accelerate along the forecast results of VAR. Overall, from the forecast trends of international Brent crude oil prices from September 2017 to December 2022, both VAR and VEC models have good forecast effects, which are coincide with the possible future developments in the international oil market and the international oil prices.
5 Conclusions and policy implications
This paper attempts to divide the whole fluctuation range of international crude oil prices from January 1990 to August 2017 into several sub-periods and examine different variables relating to each of these six groups: Economics, Fundamentals, Technology, Finance, Speculation and Geopolitics. Furthermore, we investigated the long-term relationship between international crude oil prices and selected determinants by using co-integration theory to quantitatively analyze the contribution degree of different factors to international crude oil price at different stages. Finally, we established the oil price forecast models VAR and VEC to make predictions of international oil price from January 1990 to August 2017 inside of the sample and from September 2017 to December 2022 outside of the sample.
It is demonstrated that in addition to the explained variable, international Brent oil prices, six explanatory variables are eventually specified for each influential factor groups: DJI, Oil stocks of OECD, US rotary rig count, US dollar index, TOI, Geopolitical instability, which are quoted at pbrent, dji, oeoi, rig, usdx, toi, gpo. The whole sample, January 1990 to August 2017, is divided into the 6 sub-periods January 1990 to December 1996, January 1997 to December 2002, January 2003 to December 2006, January 2007 to December 2008, January 2009 to June 2014 and July 2014 to August 2017. The breakdown is useful in that it proxies phases of key international Brent oil price developments. Secondly, after the Johansen co-integration tests for all the variables of the whole sub-periods, it can be concluded that there is one long-term stable equilibrium relationship between the international Brent crude oil prices and influential variables at the 0.05 level. In addition, from the perspective of the whole sub-periods and all the influential variables, the contribution ratios of all the influential variables to Brent crude oil prices are in accordance with the corresponding qualitative characteristics of the historical oil market and the fluctuation of oil prices. The established co-integration relation equations present stronger explanatory power. Furthermore, based on the co-integration theory, we established the oil price forecast models VAR and VEC. From January 1990 to August 2017 inside of the sample, both the static simulation results of VAR and VEC are close to the actual international Brent crude oil prices. However, the forecasts effect of VAR is better than VEC. From September 2017 to December 2022 outside of the sample, the forecast results of VAR show that annually average Brent crude oil prices for 2017–2022 are $53.0, $61.3, $74.4, $90.0, $105.5, and $120.7 per barrel, respectively. The forecast results of VEC show that annually average Brent crude oil prices for 2017–2022 are $53.0, $56.5, $58.5, $60.7, $63.0 and $65.4 per barrel, respectively. According to the market analysis and forecasts to 2022 of IEA, the downturn in investment will lead to a worldwide supply shortage of crude oil after 2020. In some sense, the forecast results of VAR and VEC are corresponding to a low reservoir development scenario and a high reservoir development of possible future developments in the international oil market and the international crude oil prices.
The drastic fluctuation of international oil price will have a significant impact on China, the second largest oil consumer and the third oil-importing country in the world. Supported by the favorable economic situation, substantial growth in petrochemical production and strong demand for car ownership, it is expected that China’s oil demand will increase by 1.8 million barrels per day in 2016–2022, with an average annual growth rate of about 2.4%. In addition, the pattern of international crude oil trade will also change. China, India and Southeast Asia will jointly push the international crude oil flow from the west to the east. In the next 5 years, China’s net daily imports of crude oil will reach 9.5 million barrels, which is next only to the United States’ record of 10 million barrels per day in the beginning of this century. Firstly, in the process of strengthening international cooperation, China should make effective use of foreign resources to ensure energy security. Secondly, the trend of the international crude oil price is needed for our country’s refined oil price adjustment. At present, China’s dependence on foreign crude oil and gas is more than 65% and 30%. The import price of crude oil in China is greatly affected by the price of international commodity futures market. With this background, China should continue to increase investment, accelerate the national strategic crude oil reserve facilities, increase enterprise reserves infrastructure, enhance the commercial crude oil storage capacity and reduce the impact of the international energy market volatility on China’s economy. Thirdly, China will strengthen cooperation with the “One Belt and One Road” initiative along the country’s energy field, which can enrich China’s imports of energy sources to deal with future complicated geopolitical situations.
References
Alhajji AF, Huettner D. OPEC and world crude oil markets from 1973 to 1994: cartel, oligopoly, or competitive? Energy J. 2000;21(3):31–60. https://doi.org/10.2307/41322890.
An H, Gao X, Fang W, et al. Research on patterns in the fluctuation of the co-movement between crude oil futures and spot prices: a complex network approach. Appl Energy. 2014;136(12):1067–75. https://doi.org/10.1016/j.apenergy.2014.07.081.
Blanco JM, Vazquez L, Pena F, et al. New investigation on diagnosing steam production systems from multivariate time series applied to thermal power plants. Appl Energy. 2013;101:589–99. https://doi.org/10.1016/j.apenergy.2012.06.060.
Bondia R, Ghosh S, Kanjilal K. International crude oil prices and the stock prices of clean energy and technology companies: evidence from non-linear co-integration tests with unknown structural breaks. Energy. 2016;101:558–65. https://doi.org/10.1016/j.energy.2016.02.031.
Breitenfellner A, Cuaresma JC, Keppel C. Determinants of crude oil prices: supply, demand, cartel or speculation? Monet Policy Econ Q. 2009;4(4):111–36.
Bunn D, Chevallier J, Pen YL, et al. Fundamental and Financial Influences on the co-movement of oil and gas prices. Energy J. 2017;38:201–28. https://doi.org/10.5547/01956574.38.2.dbun.
Chen H, Liao H, Tang BJ, et al. Impacts of OPEC’s political risk on the international crude oil prices: an empirical analysis based on the SVAR models. Energy Econ. 2016a;57(6):42–9. https://doi.org/10.1016/j.eneco.2016.04.018.
Chen H, Liu L, Wang Y, et al. Oil price shocks and U.S. dollar exchange rates. Energy. 2016b;112(10):1036–48. https://doi.org/10.1016/j.energy.2016.07.012.
Coleman L. Explaining crude oil price using fundamental measures. Energy Policy. 2012;40:318–24. https://doi.org/10.1016/j.enpol.2011.10.012.
Cong RG, Wei YM, Jiao JL, et al. Relationships between oil price shocks and stock market: an empirical analysis from China. Energy Policy. 2008;36(9):3544–53. https://doi.org/10.1016/j.enpol.2008.06.006.
Dickey DA, Fuller WA. Distribution of the estimators for autoregressive time series with a unit root. J Am Stat Assoc. 1979;74(366):427–31. https://doi.org/10.1080/01621459.1979.10482531.
Du L, He Y, Wei C. The relationship between oil price shocks and China’s macro-economy: an empirical analysis. Energy Policy. 2010;38(8):4142–51. https://doi.org/10.1016/j.enpol.2010.03.042.
Engle RF, Granger CWJ. Co-integration and error correction: representation, estimation, and testing. Econom Soc. 1987;55(2):251–76. https://doi.org/10.2307/1913236.
Ford JL, Dickinson DG. Bank loans and the effects of monetary policy in China: VAR/VECM approach. China Econ Rev. 2010;21(1):65–97. https://doi.org/10.1016/j.chieco.2009.11.002.
Gavaliere G. Testing for unit roots in bounded time series. J Econom. 2014;178(2):259–72. https://doi.org/10.1016/j.jeconom.2013.08.026.
Genc TS. OPEC and demand response to crude oil Prices. Energy Econ. 2017;66:238–46. https://doi.org/10.1016/j.eneco.2017.06.026.
Ghysels E. Macroeconomics and reality of mixed frequency data. Econometrica. 2016;193(2):294–314. https://doi.org/10.1016/j.jeconom.2016.04.008.
Granger CWJ, Newbold P. Spurious regressions in econometrics. J Econom. 1974;2(2):111–20. https://doi.org/10.1016/0304-4076(74)90034-7.
Han S, Zhang BS, Tang X, et al. The relationship between international crude oil prices and China’s refined oil prices based on a structural VAR model. Pet Sci. 2017;14:228–35. https://doi.org/10.1007/s12182-016-0139-9.
Jansson M, Nielsen M. Nearly efficient likelihood ratio tests of the unit root hypothesis. Econometrica. 2012;80(5):2321–32. https://doi.org/10.3982/ECTA10306.
Jiang CH. An empirical study on the transmission mechanism of the price of crude oil and refined oil retail price in China based on the VAR model during the period of 2003–2011. Macroecon Res. 2013;4:28–38. https://doi.org/10.16304/j.cnki.11-3952/f.2013.04.001 (in Chinese).
Jiang ZF, Jiang H. China’s oil security strategy under the shadow of high oil prices. Modern Manag Sci. 2005;8:69–70. https://doi.org/10.3969/j.issn.1007-368X.2005.03.030 (in Chinese).
Jianwei E, Bao YL, Ye JM. Crude oil price analysis and forecasting based on variational mode decomposition and independent component analysis. Physica A. 2017;484(10):412–27. https://doi.org/10.1016/j.physa.2017.04.160.
Jiao JL, Gan HH, Wei YM. The impact of oil price shocks on Chinese industries. Energy Sources Part B. 2012;7(4):348–56. https://doi.org/10.1080/15567249.2011.594852.
Johansen S. Statistical analysis of cointegration vectors. J Econ Dyn Control. 1988;12:231–54. https://doi.org/10.1016/0165-1889(88)90041-3.
Johansen S, Juselius K. Maximum likelihood estimation and inference on cointegration-with applications to the demand for money. Oxford Bull Econ Stat. 1990;52(2):169–210. https://doi.org/10.1111/j.1468-0084.1990.mp52002003.x.
Mensah L, Obi P, Bokpin G. Co-integration test of oil price and us dollar exchange rates for some oil dependent economies. Res Int Bus Financ. 2017;42:304–11. https://doi.org/10.1016/j.ribaf.2017.07.141.
Mi ZF, Wei YM, Tang BJ, et al. Risk assessment of oil price from static and dynamic modeling approaches. Appl Econ. 2017;49(9):929–39.
Miao H, Ramchander S, Wang TY, et al. Influential factors in crude oil price forecasting. Energy Econ. 2017. https://doi.org/10.1016/j.eneco.2017.09.010.
Mohaddes K, Pesaran MH. Oil prices and the global economy: Is it different this time around? Energy Econ. 2017;65:315–25. https://doi.org/10.1016/j.eneco.2017.05.011.
Moore MJ, Copeland LS. A comparison of Johansen and Phillips-Hansen cointegration tests of forward market efficiency Baillie and Bollerslev revisited. Econ Lett. 1995;47(2):131–5. https://doi.org/10.1016/0165-1765(94)00547-F.
Ng S, Perron P. Lag length selection and the construction of unit root tests with good size and power. Econometrica. 2001;69(6):1519–54.
Ouyang XL, Lin BQ. An analysis of the driving forces of energy-related carbon dioxide emissions in China’s industrial sector. Renew Sustain Energy Rev. 2015;45:838–49. https://doi.org/10.1016/j.rser.2015.02.030.
Park C, Mo C, Lee S. The effects of oil price on regional economies with different production structures: a case study from Korea using a structural VAR model. Energy Policy. 2011;39(12):8185–95. https://doi.org/10.1016/j.enpol.2011.10.018.
Pedroni P. The econometric modelling of financial time series. Econ J. 2008;96(96):339–55.
Ratti RA, Vespignani JL. Oil prices and global factor macroeconomic variables. Energy Econ. 2016;59:198–212. https://doi.org/10.1016/j.eneco.2016.06.002.
Sun JB. A study on the relationship between USD exchange rate and international oil price fluctuations-An empirical analysis on the WTI price fluctuations. The Master dissertation of Shan Dong University. 2013.
Timilsina GR. Oil prices and the global economy: a general equilibrium analysis. Energy Econ. 2015;49:669–75. https://doi.org/10.1016/j.eneco.2015.03.005.
Uri ND. Crude oil price volatility and unemployment in the United States. Energy. 1996;21(1):29–38. https://doi.org/10.1016/0360-5442(95)00086-0.
Wang Q, Sun X. Crude oil price: demand, supply, economic activity, economic policy uncertainty and wars—from the perspective of structural equation modeling (SEM). Energy. 2017;133:483–90. https://doi.org/10.1016/j.energy.2017.05.147.
Wang X, Zhang C. The impacts of global oil price shocks on China’s fundamental industries. Energy Policy. 2014;68:394–402. https://doi.org/10.1016/j.enpol.2014.01.020.
Wei YM, Wu G, Fan Y, et al. Empirical analysis of optimal strategic petroleum reserve in China. Energy Econ. 2008;30(2):290–302. https://doi.org/10.1016/j.eneco.2006.07.001.
Wu G, Zhang YJ. Does China factor matter? An econometric analysis of international crude oil prices. Energy Policy. 2014;72(9):78–86. https://doi.org/10.1016/j.enpol.2014.04.026.
Xu B, Lin BQ. Assessing CO2 emissions in China’s iron and steel industry: a dynamic vector autoregression model. Appl Energy. 2016;161:375–86. https://doi.org/10.1016/j.apenergy.2015.10.039.
Yan LY. Analysis of the international oil price fluctuations and its influencing factors. Am J Ind Bus Manag. 2012;2:39–46. https://doi.org/10.4236/ajibm.2012.22006.
Yao T, Zhang YJ, Ma CQ. How does investor attention affect international crude oil prices? Appl Energy. 2017;205:336–44. https://doi.org/10.1016/j.apenergy.2017.07.131.
Yu L, Wang Z, Tang L. A decomposition-ensemble model with data-characteristic-driven reconstruction for crude oil price forecasting. Appl Energy. 2015;156(10):251–67. https://doi.org/10.1016/j.apenergy.2015.07.025.
Zhang JL, Zhang YJ, Zhang L. A novel hybrid method for crude oil price forecasting. Energy Econ. 2015;49:649–59. https://doi.org/10.1016/j.eneco.2015.02.018.
Zhang QQ. The impact of international oil price fluctuation on China’s economy. Energy Procedia. 2011;5:1360–4. https://doi.org/10.1016/j.egypro.2011.03.235.
Zhang XB, Qin P, Chen X. Strategic oil stockpiling for energy security: the case of China and India. Energy Econ. 2017;61:253–60. https://doi.org/10.1016/j.eneco.2016.11.021.
Zhang YJ. Speculative trading and WTI crude oil futures price movement: an empirical analysis. Appl Energy. 2013;107(4):394–402. https://doi.org/10.1016/j.apenergy.2013.02.060.
Zhang YJ, Wang ZY. Investigating the price discovery and risk transfer functions in the crude oil and gasoline futures markets: some empirical evidence. Appl Energy. 2013;104(1):220–8. https://doi.org/10.1016/j.apenergy.2012.10.066.
Zhang YJ, Yao T. Interpreting the movement of oil prices: driven by fundamentals or bubbles? Econ Model. 2016;55:226–40. https://doi.org/10.1016/j.econmod.2016.02.016.
Zhang YJ, Zhang L. Interpreting the crude oil price movements: evidence from the Markov regime switching model. Appl Energy. 2015;143:96–109. https://doi.org/10.1016/j.apenergy.2015.01.005.
Zhou SR. Analysis on the factors influencing international oil price and the role of China in deciding the price. Nanjing University. 2016. (in Chinese).
Zhu XH, Chen JY, Zhong MR, et al. Dynamic interacting relationships among international oil prices, macroeconomic variables and precious metal prices. Trans Nonferr Metal Soc China. 2015;25(2):669–76. https://doi.org/10.1016/S1003-6326(15)63651-2.
Acknowledgements
The authors gratefully acknowledge that this work was supported by the National Science Foundation of China (NSFC No. 41271551/71201157) and the National Key Research and Development Program (2016YFA0602700). We are also grateful to anonymous reviewers for helpful suggestions that improved this paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Edited by Xiu-Qin Zhu
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Zhang, HL., Liu, CX., Zhao, MZ. et al. Economics, fundamentals, technology, finance, speculation and geopolitics of crude oil prices: an econometric analysis and forecast based on data from 1990 to 2017. Pet. Sci. 15, 432–450 (2018). https://doi.org/10.1007/s12182-018-0228-z
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12182-018-0228-z