1 Introduction

Tight sandstone gas (TSG) generated in tight reservoirs is one of three major types of unconventional energy. TSG has been found widely distributed worldwide and has great potential for exploration. It has a tight matrix and in general has a nanoscale pore system in which natural gas exists and migrates with a mechanism different from conventional gas reservoirs. Studies (Schloemer and Krooss 2004) have demonstrated that natural gas diffuses under the action of a concentration field and percolates under the action of a pressure field among tight matrix pores and throats, and that natural gas is released from micro- and nano-pores through three major procedures: desorption, diffusion, and percolation. Therefore, the study of desorption and diffusion mechanisms of natural gas in nanoscale tight sandstone pores is significantly important to the evaluation and development of natural gas. However, there have been very few reports about quantitative studies of diffusion and mass transfer in gas reservoirs from a microscale/nanoscale perspective although the molecular diffusion effect is a key process of the migration of tight sandstone gas.

The first diffusion equation was presented by Adolf Fick as an empirical equation where a diffusion coefficient was used to represent the speed of mass diffusion in diffusion media. Today, a large number of studies on the determination of the diffusion coefficient of natural gas in cores have been conducted by domestic and international scholars (Bird et al. 2014; Wang et al. 2014; Liu et al. 2012; Jian et al. 2012); diffusion equations have been optimized and are capable of serving at high temperature and high pressure; and diffusion coefficient values ranging from 10−12 to 10−5 m2/s have been obtained (Bera et al. 2011; Bing et al. 2013; Kelly et al. 2015; Nozawa et al. 2012). Ertekin et al. (1986) described Knudsen flow under the action of a concentration field using Fick’s Laws of Diffusion in combination with the description of gas flow in tight pores and deduced an empirical equation for the calculation of gas diffusion coefficients through the replacement of Graham’s Law of Diffusion using the Jones and Owens experimental data. Liu (2013) and Wu et al. (2012) employed a molecular simulation method to study the diffusion characteristics of CH4 and CO2. Curtis et al. (2012) built a microscale two-dimensional finite element model based on the diffusion studies of other porous materials to study the diffusion mechanism of natural gas in micro/nano-pores. Wu et al. (2015) deduced a mathematical percolation model using the infinitesimal method which is different from Darcy percolation and applies to the micro-study of tight gas in matrix pores. Javadpour and Moghanloo (2013) built a methane molecule migration model and further discussed the contribution of molecular diffusion to gas production.

Preceding studies have brought some results and progress, but these macrotheories and methods are insufficient for the description and interpretation of a micro-mechanism. There are still some unprecedented technical challenges to reproduce the migration of tight sandstone gas in micro/nano-pores for studies on percolation mechanisms. The nano-pore structure of tight sandstone reservoirs has very critical influence on gas accumulation and mass transfer, so the modeling of pores is directly related to the accuracy of numerical simulation results. However, in existing studies, models are just simplified ideal models which do not represent the real pore structure of tight gas reservoirs. In this study, a refined digital model of the pore structure of tight sandstone reservoirs was built using advanced digital core technology (Guo et al. 2016; Chen et al. 2015; Liu et al. 2014, 2017; Ni et al. 2017; Yin et al. 2016), and a numerical simulation of molecular diffusion was conducted on the basis of the model. This has provided new ideas for the study of the micro-mechanisms of molecular diffusion of tight gas.

2 TSG digital core modeling

2.1 Nano-CT experiment

Computed tomography (CT) is a technology used to nondestructively detect the internal structure of an object. It is today’s most practical and accurate method of building 3D digital cores. CT identifies the pores and skeleton based on the fact that components of different densities in the core absorb different amount of X-rays. In this study, a ZEISS Xradia 800 Ultra X-ray microscope (Fig. 1a) was used for 3D imaging. The experimental sample is φ25 × 50 mm cylindrical sample. Samples were dried before scanning. For the φ25 × 50 mm sample, to improve the sample resolution as far as possible, the scanning area of the experimental sample is φ70 × 70 μm. The sampling resolution of this Nano-CT is down to 50 nm, which enables the microscope to take 1022 two-dimensional section images (Fig. 1b) with 1016 × 1024 pixels for one sample. Each voxel has a spatial resolution of 65 nm. By superimposing these images in sequence, 3D grayscale images can be obtained (Fig. 1c), representing the microstructure of the tight sandstone samples.

Fig. 1
figure 1

The process of Nano-CT scanning technology. a Xradia 800 Ultra, b one of the CT slices, c 3D grayscale images

Full size image

2.2 Image processing

Various types of system noise exist in these grayscale images of cores, decreasing image quality and negatively affecting the subsequent quantitative analysis, so the first step of image processing is to increase the signal–noise ratio (SNR) using a filtering algorithm. For a 3D image, the commonly used filtering algorithms include low-pass linear filtering, Gaussian smoothing, and median filtering. A comparison of the filtering effects among the three algorithms has been made, and a median filter was employed in this study. In a grayscale image filtered and processed with the median filter, the transition between the pores and skeleton is natural; the boundary is smooth; and important characteristics are also retained in the image (as shown in Fig. 2). For better identification and quantization of the pores and skeleton, binary classification is required for the grayscale image using the image segmentation method. The segmentation threshold is crucial to binary classification, so it must be selected carefully. In this paper, the porosity of the core sample has already been determined through Nano-CT scan, so the best segmentation threshold obtained on the basis of the porosity can be used for image segmentation. Based on the measured porosity, the segmentation threshold k* is obtained through the following equation:

$$f\left( {k^{ * } } \right) = \hbox{min} \left\{ {f\left( k \right) = \varphi - \frac{{\sum\nolimits_{{i = I_{\text{MIN}} }}^{k} {p\left( i \right)} }}{{\sum\nolimits_{{i = I_{\text{MIN}} }}^{{I_{\text{MAX}} }} {p\left( i \right)} }}} \right\}$$
(1)

where φ is the porosity of the core, k is the gray threshold, the maximum and minimum gray values of the image are IMAX and IMIN, respectively, the number of voxels with a gray value of i is p(i), the voxels with a gray value lower than the gray threshold represent pores, the remaining represents the skeleton. Based on the final value searched, k* = 56, which is used as the segmentation threshold, binary images are obtained after segmentation. As shown in Fig. 3, the blue color represents the pores and the black-colored background represents the skeleton. If necessary, the mathematical morphological algorithm can be used for further refined processing by removing the independent voxels using open surface operations and filling the small holes using closed surface operations to connect the neighboring voxels.

Fig. 2
figure 2

The slice after median filtering

Full size image
Fig. 3
figure 3

The result of binarization (pores are blue)

Full size image

2.3 3D surface reconstruction and pore structure quantitative analysis

In this paper, the CT images measured 1016 × 1024 pixels. To reflect macropore structures and macroscopic properties, and taking into account the amount of reconstruction data generated and the associated computational burden, in this paper, a compromise involved cutting the CT images. Selecting a representative elementary volume (REV, the smallest core unit that can characterize the macroscopic physical properties of a core effectively) is crucial to the follow-up study in this paper. Repeated experiments show that when the size of a digital core model is 500 × 500 × 500 voxels, its porosity is almost unaffected by size (Fig. 4), indicating that the REV size can characterize the macroscopic physical properties of TSG.

Fig. 4
figure 4

The schematic diagram of REV analysis. a Expand the cube length progressively, b the calculation porosity change with cube length

Full size image

The Marching Cube algorithm (Lorensen and Cline 1987) is used to obtain a triangle mesh set from the 3D data cube of the image processing results and an illumination model is used to render the triangle meshes. Then, a 3D surface image of the core is formed. In this way, a 3D digital model of tight sandstone cores is built (Fig. 5).

Fig. 5
figure 5

The digital core model (3D reconstruction of pores)

Full size image

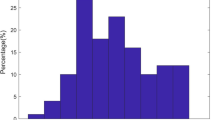
In the digital model built in the above step, most of the pores are closely contacted. It is very hard to identify the boundary of each pore, which negatively affects the subsequent quantitative statistics of pore size distribution. Therefore, the boundary of each pore must be identified and labeled. In this study, the fast watershed algorithm is used for boundary detection. Using the image as the geo-scientific topography, the gray value of each pixel on the image as the sea level elevation of the pixel, each local minimum and its affected areas as a catchment basin, and the boundary of the catchment basin as the watershed, this algorithm has enabled the identification of each pore and generated a spatially labeled graph (as shown in Fig. 6) labeling each pore independently; in this way a single pore boundary can be identified easily, which enables convenient collection of pore data for quantitative analysis. As long as the volume of each pore is determined, the porosity of the digital core can be obtained through calculation. In the meantime, assuming that the volume of a sphere is approximately equal to the volume of pores at the corresponding location, the equivalent pore size of each pore can be determined through Eq. (2) and a pore size distribution histogram can be obtained on the basis of the final statistics (Fig. 7).

$$D_{\text{eq}} = {}^{3}\sqrt {\frac{{6V_{\text{pore}} }}{\pi }}$$
(2)
Fig. 6
figure 6

The quantification and characterization of pore structure in digital coal model label image of pores

Full size image
Fig. 7
figure 7

The pore size distribution histogram

Full size image

It is shown in Fig. 7 that the pore radius of this TSG sample is mainly distributed in the range of 0.43–1 microns. At the current resolution, few 80-nm-sized pores are captured. The widespread distribution of sub-micron and nanoscale pores is the root cause of the difficulty of developing such gas reservoirs. Table 1 shows that the porosity obtained through calculation is slightly lower than the measured porosity. This error is mainly caused by image smoothing, because removing the small holes affects the calculation of porosity to some extent.

Table 1 The comparison of porosity results
Full size table

3 Numerical simulation of molecular diffusion

3.1 Theoretical foundation

3.1.1 Fick’s first law: definition of molecular diffusion

Molecular diffusion is a process whereby dissolved mass is passively transported from a higher chemical energy state to a lower chemical energy state through random molecular motion. Steady state diffusion of a chemical species in free solution can be described empirically using Fick’s first law:

$$\vec{j} = - D\cdot\vec{\nabla }c$$
(3)

where \(\vec{j}\) is the solute mass flux (in mol m−2 s−1); D is the diffusion coefficient of the solute in the solvent (in m2 s−1); c is the concentration of the solute in the solvent (in mol m−3).

3.1.2 Fick’s second law

The partial differential equation describing transient diffusion in a homogeneous (only one solid phase), saturated (the void space of the material is filled by the solvent), porous medium can be developed from the Fick’s first law and conservation of mass. This equation is called Fick’s second law and is written as follows:

$$\frac{\partial c}{\partial t} = - D\cdot\vec{\nabla }c$$
(4)

To simulate a molecular diffusivity laboratory measurement, a classical experiment is suggested, which is based on the double reservoir test. Two reservoirs having the same volume VR are positioned on each side of the sample in a chosen direction. The other directions are closed with impervious planes, so that no diffusion occurs. The initial concentrations of the reservoirs are different: Cin (t) and Cout (t). The sample is initially filled with the solution at Cin (t0), t0 being the instant when the experiment starts. At time t = t0, the reservoirs are connected to the sample and the diffusion process starts. The influence of gravity is neglected, only passive diffusion is considered, not advection.

Considering these boundary conditions, Fick’s second law governs the diffusion and defines the concentration field in the sample. The concentration of the reservoirs also evolves since they have a finite volume VR. By default, VR is supposed to be 100 times higher than the void space volume in the sample. Let us note β = \(\frac{{V_{\text{voidspace}} }}{{V_{\text{R}} }}\), the ratio of the void space volume and the reservoir volume. The following equations govern the concentration in the reservoirs:

$$V_{\text{R}} \frac{{\partial C_{\text{in}} (t)}}{\partial t} = D\int_{{S_{\text{in}} }} {\vec{\nabla }c\cdot\vec{n}{\text{d}}S}$$
(5)
$$V_{\text{R}} \frac{{\partial C_{\text{out}} (t)}}{\partial t} = - D\int_{{S_{\text{out}} }} {\vec{\nabla }c\cdot\vec{n}{\text{d}}S}$$
(6)

where Sin and Sout are the faces of the sample where the reservoirs are connected.

Once the diffusion process starts, the concentration in the sample quickly evolves and the exchanges with the reservoirs are asymmetrical. This transient state is then replaced by an established state, when the exchanges with the reservoirs are equal.

This established state is characterized by the fact that \(\frac{{\partial C_{\text{in}} (t)}}{\partial t}\) = − \(\frac{{\partial C_{\text{out}} (t)}}{\partial t}\). Once this state is attained, the concentration in the reservoirs will continue to vary until they reach an equilibrium concentration c ∞ . The difference of these concentrations, Cout(t) − Cin(t), follows an exponential law:

$$C_{\text{out}} (t) - C_{\text{in}} (t) = p\cdot\exp ( - \lambda^{2} t)$$
(7)

where p and λ2 are constant coefficients to be determined.

An analytic solution to this problem is suggested:

$$c(X,t) = A\left[ {\left[ {\frac{{\cos \left( {\frac{\lambda }{{\sqrt {D_{\text{app}} } }} - 1} \right)}}{{\sin \left( {\frac{\lambda }{{\sqrt {D_{\text{app}} } }}} \right)}}} \right]\cos \left( {\frac{\lambda }{{\sqrt {D_{\text{app}} } }}X} \right) + \sin \left( {\frac{\lambda }{{\sqrt {D_{\text{app}} } }}X} \right)} \right]\exp ( - \lambda^{2} t) + c_{\infty }$$
(8)

where c(X, t) is the local concentration at position X and time t, A is a constant coefficient.

Knowing this solution must verify the previous hypothesis of flux equality (\(\frac{{\partial C_{\text{in}} (t)}}{\partial t}\) = − \(\frac{{\partial C_{\text{out}} (t)}}{\partial t}\)), the following equation is derived:

$$- \lambda^{2} \frac{{\cos \left( {\frac{\lambda }{{\sqrt {D_{\text{app}} } }} - 1} \right)}}{{\sin \left( {\frac{\lambda }{{\sqrt {D_{\text{app}} } }}} \right)}} = D_{\text{app}} \beta \frac{\lambda }{{\sqrt {D_{\text{app}} } }}$$
(9)

which links the λ2 coefficient to the apparent diffusivity Dapp of the sample.

To sum up:

  1. 1.

    A first transient state during which the diffusion process starts must be achieved before an established state appears.

  2. 2.

    Once the established state has begun, the difference of the reservoir concentrations follows an exponential law. Therefore, the slope of the linear curve followed by ln(Cout (t) − Cin (t)) can be estimated easily.

  3. 3.

    This slope is λ2, the exponential coefficient, which is related to the apparent diffusivity Dapp.

3.1.3 Volume averaged form of Fick’s law

The effective molecular diffusivity tensor gives global information about the diffusion capabilities of the material. A change of scale to get equations valid for the entire volume is necessary. The method of volume averaging is a technique that accomplishes a change of scale. Its main goal is to spatially smooth equations by averaging them over a volume.

This theory develops a closure problem that transforms the Fick equations to a vectorial problem; closure variable \(\overrightarrow {b}\) is used to state the concentration perturbation in a new problem:

$$\nabla^{2} \overrightarrow {b} = 0$$
(10)

When the problem is solved, it is possible to compute the dimensionless diffusivity tensor defined as:

$$\phi \frac{{\overrightarrow {{\overrightarrow {D} }} }}{{D_{\text{solution}} }} = \phi \left( {\overrightarrow {{\overrightarrow {I} }} + \frac{1}{{V_{\text{f}} }}\int_{{S_{\text{fs}} }} {\overrightarrow {{n_{\text{fs}} }} } \overrightarrow {b} {\text{d}}S} \right)$$
(11)

where \(\phi\) is the porosity; Dsolution is the bulk solution diffusivity; Vf is the volume of fluid; Sfs is the area of the fluid–solid interface; \(\overrightarrow {{n_{{{\text{fs}}}} }}\) is the normal to the fluid–solid interface directed from the fluid to the solid phase.

3.1.4 Boundary conditions

In the molecular diffusivity experiment simulation based on the solution of Fick’s equations, the rate of reaction of the solid is assumed to be zero: there is no reaction occurring at the fluid–solid interface. Then the boundary condition at fluid–solid interface is:

$$- \overrightarrow {{n_{{{\text{fs}}}} }} \cdot\overrightarrow {\nabla c} = 0$$
(12)

where \(\overrightarrow {{n_{\text{fs}} }}\) is the normal to the fluid–solid interface directed from the fluid to the solid phase.

Besides this fluid–solid interface condition, a one-voxel-wide plane of solid is added on the faces of the image that are not perpendicular to the main diffusion direction. This allows isolation of the sample from the outside.

Boundary conditions at inlet and outlet require knowledge of the concentrations in the reservoirs. These concentrations evolve over time:

$$V_{\text{r}} \frac{{\partial C_{\text{in}} }}{\partial t} = \int_{{S_{\text{in}} }} {\overrightarrow {{n{S}_{\text{in}} }} \cdot\overrightarrow {\nabla } c{\text{d}}S}$$
(13)
$$V_{\text{r}} \frac{{\partial C_{\text{out}} }}{\partial t} = - \int_{{S_{\text{out}} }} {\overrightarrow {{n{S}_{\text{out}} }} \cdot\overrightarrow {\nabla } c{\text{d}}S}$$
(14)

when Sin and Sout are, respectively, the input and output face of the sample; \(\overrightarrow {{n{S}_{\text{in}} }}\) and \(\overrightarrow {{n{S}_{\text{out}} }}\) are, respectively, the normal to the input and output face.

In the molecular diffusivity tensor calculation by volume averaging, the vectorial problem that is solved in this case is closed by imposing periodic boundary conditions to \(\overrightarrow {b}\) and the geometry. The fluid–solid interface condition has the following similar form:

$$- \overrightarrow {{n_{\text{fs}} }} \cdot\overrightarrow {\nabla } \overrightarrow {b} = \overrightarrow {{n_{\text{fs}} }}$$
(15)

Then, we used a finite volume method to solve the equation systems. The finite volume method (FVM) is a method for representing and evaluating partial differential equations in the form of algebraic equations. Similar to the finite difference method or finite element method, values are calculated at discrete places on a meshed geometry. “Finite volume” refers to the small volume surrounding each node point on a mesh. In the finite volume method, volume integrals in a partial differential equation that contain a divergence term are converted to surface integrals, using the divergence theorem. These terms are then evaluated as fluxes at the surfaces of each finite volume. Because the flux entering a given volume is identical to that leaving the adjacent volume, these methods are conservative. Another advantage of the finite volume method is that it is easily formulated to allow for unstructured meshes. The method is used in many computational fluid dynamics packages. In this paper, the discretization scheme assumes that the voxel is isotropic (cubic). Once discretized, the closure equation system can be written as Ax = b, A being a sparse, symmetric matrix. The equation system is solved using a fully implicit method (matrix inversion). The PETSc (Portable, Extensible Toolkit for Scientific Computation) library is used for the direct resolution of the linear system. An iterative resolution with a conjugate gradient and ILU (Incomplete lower and upper triangular factorization method) preconditioner is performed. The convergence criterion used is the relative decrease of the residual l 2 -norm.

3.2 The result of molecular diffusivity simulation

The default parameters simulate an experiment along the Z axis with a concentration in the input reservoir at initial time of 1711 mol m−3 (Cin (t) = 1711 mol m−3) and the concentration in the output reservoir at initial time being null (Cout (t) = 0). The default solution bulk diffusivity is 1 m2 s−1. Then, the direction of the molecular diffusion can be adjusted to X, Y, or Z direction. If several directions are selected, the computations will be done successively. The concentration values used as boundary conditions of the experiment can also be modified. Modifying these values will not change the molecular diffusivity, which is intrinsic to the porous medium. It will only modify the output concentration field.

The resulting visualization in X, Y, and Z direction, respectively, should look like Fig. 8. We can observe the decrease of the concentration from the input reservoir (in yellow), to the output reservoir (in light blue).

Fig. 8
figure 8

Visualization of the concentration field in an experiment simulation with molecular diffusion

Full size image

With these parameters, we compute the full intrinsic diffusivity tensor. A full tensor computation requires three computations, each equivalent in time and memory consumption to one experiment simulation. Experiment simulation in each direction gives the following results (shown in Table 2).

Table 2 The computed results of molecular diffusivity
Full size table

3.3 Comparison results

We base our validation on several studies reporting the results of molecular diffusivity experimental measurements and empirical laws aimed at computing the molecular diffusivity of a material. Glemser (2008) reported the following analytical estimations of molecular diffusivity with respect to the porosity \(\phi\):

$${\text{Maxwell}}\;\left( {1881} \right):\phi \frac{D}{{D_{\text{solution}} }} = \frac{2\phi }{3 - \phi }$$
(16)
$${\text{Weissberg}}\;\left( {1963} \right):\phi \frac{D}{{D_{\text{solution}} }} = \frac{\phi }{1 - \ln (\phi )/2}$$
(17)

We compare our values to the values computed with empirical laws [Eqs. 16, 17)] and the analytic solution. All these results are displayed in Fig. 9. It can be seen from Fig. 9 that our computed result is in good agreement with the other results as well as the analytic solution.

Fig. 9
figure 9

Comparison of empirical laws and numerical simulations for the determination of molecular diffusivity with respect to the porosity

Full size image

4 Conclusions

  1. 1.

    Nano-CT scanning can be used to photograph the true pore structure of tight sandstone. The image segmentation method based on experiment-measured porosity is established to binarize the digital image of tight sandstone.

  2. 2.

    The pore size distribution is obtained based on the digital core model of tight sandstone. It has been found that the radii of pores of this sample are mainly distributed in the range of 0.43–1 microns, and few 80-nm-sized pores are captured at the current resolution.

  3. 3.

    By the use of finite volume method, the molecular diffusion process of gas in real pore space can be simulated visually based on the digital core model of tight sandstone, and the diffusion coefficient can also be calculated, which is in good agreement with the others’ empirical laws results.

With the development of computer technology, digital rock physics will become an important technical means to participate in the exploration and development of tight oil and gas. Our study provides a new research method for digital rock physics of tight sandstone. It is a foundation work for the future tight gas percolation theory and numerical simulation research.