Abstract
The fracture gradient is a critical parameter for drilling mud weight design in the energy industry. A new method in fracture gradient prediction is proposed based on analyzing worldwide leak-off test (LOT) data in offshore drilling. Current fracture gradient prediction methods are also reviewed and compared to the proposed method. We analyze more than 200 LOT data in several offshore petroleum basins and find that the fracture gradient depends not only on the overburden stress and pore pressure, but also on the depth. The data indicate that the effective stress coefficient is higher at a shallower depth than that at a deeper depth in the shale formations. Based on this finding, a depth-dependent effective stress coefficient is proposed and applied for fracture gradient prediction. In some petroleum basins, many wells need to be drilled through long sections of salt formations to reach hydrocarbon reservoirs. The fracture gradient in salt formations is very different from that in other sedimentary rocks. Leak-off test data in the salt formations are investigated, and a fracture gradient prediction method is proposed. Case applications are examined to compare different fracture gradient methods and validate the proposed methods. The reasons why the LOT value is higher than its overburden gradient are also explained.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 Concept of fracture gradient
For drilling in the oil and gas industry and geothermal exploration and production, fracture pressure is the pressure required to fracture the formation and to cause mud losses from a wellbore into the induced fractures. Fracture gradient is obtained by dividing the true vertical depth into the fracture pressure. The fracture gradient is the upper bound of the mud weight; therefore, the fracture gradient is an important parameter for mud weight design in both stages of drilling planning and operations. If the downhole mud weight is higher than the formation fracture gradient, then the wellbore will have tensile failures (i.e., the formation will be fractured), causing losses of drilling mud or even lost circulation (total losses of the mud). Therefore, fracture gradient prediction is directly related to drilling safety.
In drilling engineering, the pore pressure gradient and fracture gradient are two most important parameters practically used for determining the mud weight (or mud density) window, as shown in Fig. 1. The mud weight should be appropriately selected based on the pore pressure gradient, wellbore stability, and fracture gradient prior to setting a casing. The drilling mud is applied in the form of mud pressure to support borehole walls for preventing formation fluid influx and wellbore collapse during drilling. To avoid fluid influx, pressure kicks, and wellbore instability in an open-hole section, a heavier downhole mud weight than the pore pressure gradient is required. For offshore drilling, the US Bureau of Safety and Environmental Enforcement (BSEE) requires that the downhole mud weight is higher than the pore pressure gradient and “static downhole mud weight must be a minimum of 0.5 lb per gallon (ppg) below the lesser of the casing shoe pressure integrity test or the lowest estimated fracture gradient” (the red dash lines shown in Fig. 1). Otherwise, the hole is undrillable except when applying wellbore strengthening technology (Alberty and McLean 2004; Zhang et al. 2016).
If the mud weight is higher than the fracture gradient of the drilling section, it may fracture the formation, causing mud losses. To prevent mud losses caused by high mud weight, as needed where there is overpressure, a safe drilling mud weight margin is needed. Otherwise, a casing needs to be set to protect the overlying formations from being fractured, as demonstrated in Fig. 1.
Fracture gradient is defined by the Schlumberger Oilfield Glossary as the pressure gradient required to induce fractures in the rock at a given depth. Based on this definition, the fracture gradient is the maximum mud weight that a well can hold without mud losses and without uncontrolled tensile failures (fracture growth). However, there is no consensus for a method to calculate the fracture gradient in the oil and gas industry. Some pore pressure specialists use the minimum stress gradient as the fracture gradient, but others may use the maximum leak-off pressure gradient (fracture breakdown pressure gradient) or the fracture initiation pressure gradient as the fracture gradient. In this paper, the maximum leak-off pressure gradient (the peak value in the LOT test) is used as the fracture gradient. That is, the effects of the minimum stress, tensile strength, and the wellbore stress concentrations will be considered for fracture gradient prediction.
1.2 Fracture gradient from leak-off tests
Typically, a formation pressure integrity test or the formation leak-off test is performed in drilling operations to evaluate cement jobs, determine the casing setting depth, test the resistance of tensile failures of a casing shoe, and estimate formation fracture gradient (Postler 1997). Based on the injection pressure, volume, and time, pressure integrity tests can be classified into three, i.e., formation integrity test (FIT), leak-off test (LOT), and extended leak-off test (XLOT). The purpose of conducting a FIT is to test the formation fracture pressure required for kick tolerance and/or safe drilling mud weight margin. The maximum pressure in the FIT test is less than the fracture initiation and formation breakdown pressures.
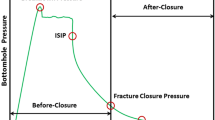
In a XLOT test at a casing shoe, only the open hole below the casing and any new formation (~10 ft) drilled prior to the test are exposed (Edwards et al. 2002) to the injection fluid that is pumped at a constant rate. The pressure increase in the hole is typically linear as long as there are no leaks in the system, and the exposed formation is not highly permeable. At some point, the rate of pressurization changes such that the pressure–time curve departs from linearity, as shown in Fig. 2a. This departure from linearity is referred to as the fracture initiation pressure (P i). The pressure is then typically seen to increase at a lower rate until a maximum pressure is reached, i.e., the breakdown pressure (P b). After this point, the pressure falls rapidly or remains steady. After the rock is broken down (hydraulic fracture created), at some point the pressure in the hole levels off and remains fairly constant (P prop) at the same flowrate; the fracture is propagating. When the pump is turned off, the pressure immediately drops to the instantaneous shut-in pressure (P isip). After the well is shut in, the pressure begins to decline as the fracture starts to close; the stress acting to close the fracture is the closure pressure (P c) or the minimum stress (σ min). To obtain more data, a second pressurization cycle may then be performed. Because a fracture has been created by the first cycle of XLOT, there is no tensile strength in the fracture reopening (Zhang and Roegiers 2010).
For a typical LOT test, once the peak pressure, or the breakdown pressure (P b), is reached, the pump is shut down to record the 10-s pressure reading and then, shut-in pressure is continuously recorded for more than 10 min, as shown in Fig. 2b. Fracture pressures can be measured directly from LOT, XLOT, or other similar tests, e.g., mini-frac test and diagnostic fracture injection test (DFIT).
1.3 Fracture gradient and mud losses in drilling operations
Understanding the mechanism of mud losses while drilling can help to better determine the fracture gradient. The possible reasons of mud losses in drilling operations are presented in the following cases. For different cases, the methods for mud loss control and fracture gradient design are different.
Case 1 Seepage mud loss: For permeable rocks (excluding those with highly fractured preexisting fractures), once the mud pressure applied in the borehole is greater than the formation pore pressure (p mud > p), the mud will invade and flow into the formation through pores due to high permeability. This is the seepage mud loss, which can easily happen in permeable sandstones and limestones, particularly for the low pore pressure or depleted reservoirs. Seepage mud loss is a slow mud volume escape or loss into the formation through porous materials or small holes. Therefore, seepage loss in most cases is minimal (normally, the loss <10 bbl/h for oil-based mud and <25 bbl/h for water-based mud). This will have little effect on the drilling operations. Since the seepage mud loss is mainly caused by the connected pores or by formation permeability, lost circulation material (LCM) pills can be used to block the flow path.
Case 2 Small loss: If the mud pressure is greater than the fracture initiation pressure, but less than the breakdown pressure (P i ≤ p mud < P b) in the intact shale, there will be only small volume of drilling fluid lost into the well. It can be seen from the LOT tests in Fig. 2 that it only needs 0.3 bbls of fluid pumped into the well from the initiation pressure (P i) to the breakdown pressure (P b). Therefore, mud loss is minor in this case.
Case 3 Partial loss: If the mud pressure is slightly greater than the fracture breakdown pressure (p mud ≥ P b) in the intact shale, this will be a situation when some volume of drilling fluid is lost into the formation, but some drilling mud volume still circulates back to the surface. In this case, the fluid volume not only has losses, but it may also have the ballooning issue to deal with. However, this type of fluid loss will not lead to a well control situation because the total hydrostatic pressure of the mud does not decrease.
Case 4 Partial loss and total loss in natural fractures: Once the mud pressure is greater than the minimum stress (p mud > σ min) in the preexisting uncemented fractures, the fractures will open and the mud will flow into the natural fractures. The degree of mud loss depends on both fracture properties (e.g., fracture aperture and spacing) and the difference of the mud pressure and the minimum stress.
Case 5 Total loss or lost circulation: It occurs either in intact rocks with p mud ≫ P b or in the rocks having preexisting natural fractures and faults with p mud > σ min. This is the worst situation because there is no mud returning to surface and the mud level will drop to any level down in the hole. Losing a lot of drilling fluids into the well will directly affect hydrostatic pressure at the bottom. If the mud cannot be kept full in the hole, it might be a time when the hydrostatic pressure of the mud is less than the reservoir pressure. Eventually, a well control situation will happen.
It should be noted that mud loss mechanisms described above are mainly for clastic formations but may not be relevant to carbonate formations. Some carbonate reservoirs contain different sizes of vugs or caves which are interconnected by natural fractures. As a result, a large amount of mud could be lost once the drilling mud weight is greater than the reservoir pressure (p mud > p). Therefore, the fracture gradient in this case is not much higher than the reservoir pressure. In the following study, we will not consider this case.
Therefore, for most cases, the fracture gradient (FG) should be equal to or less than the breakdown pressure gradient (i.e., FG ≤ P b) to avoid uncontrollable mud losses.
2 Some current methods for fracture gradient prediction
2.1 Hubbert and Willis' method
The concept and calculation of fracture gradient probably first came from the minimum injection pressure proposed by Hubbert and Willis (1957). They assumed that the minimum injection pressure to hold open and extend a fracture is equal to the minimum stress:
where \(P_{\text{inj}}^{ \hbox{min} }\) is the minimum injection pressure; \(\sigma_{\text{h}}^{\prime }\) is the effective minimum stress; σ h is the minimum stress; and p is the pore pressure.
Hubbert and Willis (1957) assumed that under conditions of incipient normal faulting, the effective minimum stress is horizontal and has a value of approximately one-third of the effective overburden stress, i.e., \(\sigma_{\text{h}}^{\prime } = (\sigma_{\text{V}} - p)/3\). Therefore, they obtained the minimum injection pressure or fracture pressure in the following form:
where \(\sigma_{\text{V}}\) is the vertical stress.
Later on, many empirical and theoretical equations and applications for fracture gradient prediction were presented (Haimson and Fairhurst 1967; Matthews and Kelly 1967; Eaton 1969; Anderson et al. 1973; Althaus 1997; Pilkington 1978; Daines 1982; Breckels and van Eekelen 1982; Constant and Bourgoyne 1988; Aadnoy and Larson 1989; Wojtanowicz et al. 2000; Barker and Meeks 2003; Fredrich et al. 2007; Wessling et al. 2009; Keaney et al. 2010; Zhang 2011; Oriji and Ogbonna 2012). We only review some commonly used methods in the following sections. It should be noted that the Biot coefficient is usually assumed to be 1 in fracture gradient calculation in the oil and gas industry; therefore, the Biot coefficient is not considered in the related equations. In this paper, we follow the same practice except the Biot coefficient is existed in a specific equation.
2.2 Matthews and Kelly’s method
Matthews and Kelly (1967) introduced a variable of the “matrix stress coefficient (k 1),” equivalent to effective stress coefficient, for calculating the fracture gradient of sedimentary formations:
where OBG is the overburden stress gradient; P p is the pore pressure gradient; and k 0 is the matrix stress or effective stress coefficient (it was k 1 in their original equation).
In their paper, Matthews and Kelly (1967) obtained k 0 from the fracture initiation pressures. Therefore, this fracture gradient is higher than the fracture extension gradient (the minimum stress gradient).
2.3 Eaton’s method
Eaton (1969) used Poisson’s ratio of the formation to calculate the fracture gradient based on the concept of the minimum injection pressure proposed by Hubbert and Willis (1957):
where ν is Poisson’s ratio, which can be obtained from the compressional and shear velocities (v p and v s), and
Eaton’s method enables the consideration of the effect of different rocks (e.g., shale, sandstone) on fracture gradient, because the lithology effect is considered in Poisson’s ratio calculated from Eq. (5). In fact, Eq. (4) is the equation of the minimum value of the minimum stress derived from a uniaxial strain condition (Zhang and Zhang 2017). However, in the industry applications apparent Poisson’s ratios can be used for simplification in different rocks to calculate fracture gradients, e.g., using ν = 0.43 for shales \(\left( {{\text{or}}\,\frac{\nu }{{1 - \nu }} = 0.75} \right)\) and ν = 0.3 for sandstones \(\left( {{\text{or}}\, \frac{\nu }{{1 - \nu }} = 0.5} \right)\). In this case, Eaton’s equation is equivalent to Matthews and Kelly’s equation if \(k_{0} = \frac{\nu }{1 - \nu }\).
For some old formations, such as the Cretaceous-aged and older formations, Eaton’s method [Eq. (4)] with Poisson’s ratios calculated from sonic logs [Eq. (5)] is applicable, as shown in Fig. 3 (Zhang and Wieseneck 2011). The calculated fracture gradient from Eaton’s method in Fig. 3 is compared to the measured fracture gradient results from DFIT and LOT data in some shale gas wells. In Fig. 3, the DFIT and LOT measurements and pore pressures in offset wells are depth-shifted to a target well based on the same formation tops in those offset wells and plotted in the pressure form. The fracture pressure in Fig. 3 is calculated from Eaton’s method [Eq. (4)] using the measured pore pressures from the influx and kicks in the offset wells, and Poisson’s ratios are calculated from the sonic logs using Eq. (5). The calculated fracture pressures (FP) match the measured DFIT and LOT data (Fig. 3).
Measured DFIT and LOT pressure data compared to the fracture pressure profile calculated from Eaton’s method [Eq. (4)] plotted on the same formation tops in Haynesville shale gas wells. Circles and triangle are the fluid kicks and influx in the offset wells. TVD KB presents the true vertical depth below Kelly bushing
2.4 Daines’ method
Daines (1982) superposed a horizontal tectonic stress σ t onto Eaton’s equation. Expressing in the stress form, he called it as “minimum pressure within the borehole to hold open and extend an existing fracture,” which can be written in the following equation:
where σ f is the fracture pressure; σ t is the superposed horizontal tectonic stress and a function of effective vertical (overburden) stress, i.e., \(\sigma_{\text{t}} = \beta (\sigma_{\text{V}} - p)\); and β is a constant. Therefore, Daines’ equation can be rewritten in the following form:
2.5 Fracture gradient from wellbore tensile failure
For a vertical well, the tensile failure pressure can be calculated from Kirsch’s wellbore solution in the case of non-penetrating fluid (impermeable case), as shown in Eq. (8) by Haimson and Fairhurst (1967). They called this pressure the formation breakdown pressure:
where P b is the breakdown pressure; σ h and σ H are the minimum and maximum horizontal stresses, respectively; and T 0 is the tensile strength of the rock.
In the case of penetrating fluid (permeable case), Detournay and Cheng (1988) proposed the following equation to calculate the breakdown pressure, which represents a lower bound of the breakdown pressure:
where η is a poroelastic coefficient ranging from 0 to 0.5 and \(\eta = \alpha_{\text{b}} (1 - 2\nu )/[2(1 - \nu )]\); α b is the Biot coefficient; and ν is drained Poisson’s ratio.
For example, in a case of \(\alpha_{\text{b}} = 0.8\), \(\nu = 0.3\), and \(\eta = 0.23\), the breakdown pressure is \(P_{\text{b}} = 0.65(3\sigma_{\text{h}} - \sigma_{\text{H}} - 0.46p + T_{0} )\). Compared to Eq. (8), the breakdown pressure in the permeable case is smaller than that in the impermeable case.
For inclined boreholes (including horizontal wells) and considering temperature effect (σ T), Eq. (8) can be approximately written in the following form:
and
where σ T is the steady-state thermal stress caused by the difference of the mud temperature (T mud) and formation temperature (T f); α T is the coefficient of thermal expansion of the formation; σ max and σ min are the maximum and minimum far-field stresses in the borehole cross section perpendicular to the hole axis, and they can be approximately obtained from the following equations if the shear stresses are neglected in the inclined wells (Zhang 2013):
where i is the borehole inclination, for a vertical well i = 0° and for a horizontal well i = 90°; α is the angle of drilling direction with respect to the maximum horizontal stress (σ H) direction of the borehole.
Equation (10) indicates that a higher mud temperature can increase the formation breakdown pressure, namely increase the fracture gradient.
2.6 Upper and lower bounds of fracture gradient
If neglecting temperature effects and assuming \(\sigma_{\hbox{max} } - T_{0}\) is approximately equal to σ min, Eq. (8) can be simplified to the following form (Zhang 2011):
where
Equation (12) can be used as the upper bound of fracture pressure (or gradient), and Eaton’s method [or the minimum stress method, Eq. (13)] can be used as the lower bound of fracture pressure (or gradient) (Zhang et al. 2008; Zhang 2011). The average of the lower bound and upper bound of fracture pressures can be used as the most likely fracture pressure (Zhang 2011)
where p avg is the most likely fracture pressure.
3 Improved methods for fracture gradient prediction
We start this section with the following quotation (Althaus 1997), “the purpose of this paper is to open this topic up to discussion again and to turn new studies into new directions. The old solutions have served us well in fracture gradient prediction for many years—but are they really the final answers to this problem?”.
3.1 Evaluation of Matthews and Kelly’s method
We analyze more than two hundred publicly available LOT datasets (total of 229) from exploration and production drilling wells in several offshore petroleum basins (the Gulf of Mexico, the North Sea, South America, Gulf of Guinea, and Asia). The leak-off test data are chosen only for those tests in which each test passed the initiation pressure, then reached a peak pressure value (here called LOT value) (i.e., excluding FIT tests), and performed in shale or shaly formations, excluding those tests conducted in sandstones or other permeable formations. It should be noted that most of the data are from LOT tests, and only some are from XLOT tests; therefore, the peak pressure values of the tests (LOT values) may not be the breakdown pressures, but greater than the initiation pressures. These wells are located in young sediments, mostly in Neogene and Paleogene formations and in the normal faulting stress regime. In this paper, we assume that the LOT is the measured fracture gradient; therefore, we can obtain an empirical relationship of the fracture gradient by analyzing the LOT datasets. To analyze the LOT, OBG, and P p relationship, we plot the net LOT pressure or effective LOT pressure gradient (LOT − P p) versus effective overburden stress gradient (OBG − P p) for all 229 LOT datasets in which the pore pressures and overburden stresses are reliable (Fig. 4).
We then plot the effective stress coefficient \(k_{0} = ({\text{LOT}} - P_{\text{p}} )/({\text{OBG}} - P_{\text{p}} )\) in Fig. 4. It shows that most data points are located within k 0 = 0.5–1. The average value of the effective stress coefficient from k 0 = 0.5–1 is k 0 = 0.75. Therefore, k 0 = 0.75 can be used as the most likely value to calculate the fracture gradient by plugging k 0 = 0.75 into Matthews and Kelly’s equation [Eq. (3)].
3.2 Improved fracture gradient prediction
Figure 4 shows that k 0 is scattered and not a constant. The scattered k 0 is mainly caused by that the LOT data were from different basins. For a specific basin or oil field, the LOT data should not be so scattered. To analyze what factor mostly affects variable k 0, we calculate the k 0 value in each measured LOT data point as presented in Fig. 4 based on \(k_{0} = ({\text{LOT}} - P_{\text{p}} )/({\text{OBG}} - P_{\text{p}} )\). Then, we plot the k 0 values versus depths in Fig. 5. It demonstrates that k 0 depends highly on the depth, and the wells in Green Canyon of the Gulf of Mexico have higher LOT values, but the wells in the North Sea and Gulf of Guinea have lower LOT values. Figure 5 indicates that k 0 has a higher value at a shallower depth and decreases as the depth increases, i.e., k 0 is depth dependent. Therefore, the fracture gradient is also depth dependent. The k 0 value from the LOT data in Fig. 5 can be written in the following form:
where Z is the depth below the mud line or below the sea floor; k 0 is the effective stress coefficient, which is dependent on the depth:
-
For the low case of the fracture gradient: k = 0.5, a = 0.1, and b = 5100 (left line in Fig. 5);
-
For the high case of the fracture gradient: k = 0.9, a = 0.4, and b = 12,500 (right line in Fig. 5);
-
For the most likely case of the fracture gradient: k = 0.75, a = 0.15, and b = 7200 (middle line in Fig. 5).
Normally the fracture gradient in sandstones is lower than that in shales. Based on our field applications, the low case of k 0 shown above may be used for estimating the most likely case of fracture gradient in sandstones or sandy formations.
It should be noted that k 0 varies markedly in different basins or fields; therefore, the parameters of k, a, and b in Eq. (15) should be obtained from each field for a better application if the measured LOT data are available.
Based on this depth-dependent k 0, the improved fracture gradient of Matthews and Kelly’s method can be written in the following form if we use the measured LOT data to predict the fracture gradient in the new wells:
where k, a, and b are variables, which can be determined from the LOT data in offset wells. From the data shown in Fig. 5, the following parameters can be used:
-
For the most likely case of the fracture gradient in shales: k = 0.75, a = 0.15, and b = 7200.
3.3 Fracture gradient in salt formations
For subsalt wells in the Gulf of Mexico and other petroleum basins, drilling needs to penetrate thick salt formations to reach the hydrocarbon reserves. Salt creep in the subsalt wells is a challenge for borehole stability (Zhang et al. 2008); therefore, a heavier mud weight (e.g., mud weight can be as high as 80%–90% of the overburden stress) needs to be used to control salt creep. This high mud weight requires a higher fracture gradient in the salt formation to avoid salt being fractured.
LOT and FIT data in salt formations in 15 wells in the Gulf of Mexico (10 in the Mississippi Canyon and 5 in the Green Canyon) are examined and presented in Fig. 6. It shows that the LOT and FIT pressures in most salt formations are larger than the overburden stress (\(\sigma_{\text{V}}\)), but less than \(\sigma_{\text{V}} + 1000\) psi. Therefore, the following equation can be used to estimate the fracture gradient in the salt formation:
where \(\sigma_{\text{V}}\) is the overburden stress (or OBP) in psi; C is a variable and varies from 0 to 1000 psi based on the data shown in Fig. 6, and for the most likely case, C = 500 psi.
The salt fracture gradient estimated from Eq. (17) compared to the measured FIT data in salt in a subsalt well in the Gulf of Mexico. In the presalt and subsalt formations, the proposed method [Eq. (16)], Eaton’s method, and Matthews and Kelly’s method of k 0 = 0.75 (FG MK0.75) are applied to estimate fracture gradients. MDT represents the measured pore pressures, and MW is the mud weight
It should be noted that Eq. (17) is an empirical equation only for salt formations. If inclusions of rocks exist in salt formations (e.g., in salt sutures), the fracture gradient should be lower and depend on the fracture gradient in the rocks. A case study shown in Fig. 7 examines the fracture gradients in salt, presalt, and subsalt formations. The salt fracture gradient is estimated from Eq. (17) with C = 500 psi, which matches the measured FIT data in the salt. In the subsalt formations, Eaton’s method underestimates the fracture gradient based on the measured data, but the proposed fracture gradient with a depth-dependent k 0 [Eq. (16)] has a better estimate on the fracture gradient.
3.4 Reasons of LOT being greater than OBG
It is often found that some LOT values in the leak-off tests are greater than their overburden stress gradients (i.e., LOT > OBG), for example in the Green Canyon area of the Gulf of Mexico and in some subsalt formations. These may be caused by the following reasons: (a) the measured LOT value is the formation breakdown pressure and (b) the formation is in tectonic stress regimes.
3.4.1 LOT value being the formation breakdown pressure
The LOT value reported from the LOT test may be the formation breakdown pressure in which the rock has a high tensile strength. In this case, the formation breakdown pressure in a vertical well may be calculated from Eq. (8). An example is presented in Fig. 8 for illustration. At the depth of 10,800 ft, if the minimum horizontal stress gradient σ h = 12.8 ppg, the maximum horizontal stress gradient σ H = 13.4 ppg, pore pressure gradient P p = 11 ppg, and tensile strength T 0 = 100 psi, then the breakdown pressure can be calculated from Eq. (8), i.e., the breakdown pressure gradient is P b = 14.18 ppg. However, the overburden gradient at this depth is OBG = 13.9 ppg, as shown in Fig. 8. Therefore, the breakdown pressure gradient (i.e., P b = 14.18 ppg) is greater than the overburden gradient (or \({\text{LOT}} > {\text{OBG}}\)). The measured LOT value in Fig. 8 at the depth of 10,800 ft is 14.1 ppg, similar to the calculated result.
Measured LOT data plotted with depth versus the estimated high-side, most likely, and low-case fracture gradients (FG_High, FG_ML, FG_Low) from Eq. (16) in a deepwater Gulf of Mexico well
Figure 8 plots the estimated and measured pore pressure, surface mud weight, calculated and verified overburden stress, and measured LOT values. It also plots the calculated fracture gradient bounds (high, most likely, and low cases) from the proposed method [Eq. (16)]. The figure shows that although one of the measured LOTs is greater than the overburden, all LOT data are within the calculated fracture gradient bounds.
3.4.2 In tectonic stress regimes
When formations are in tectonic stress regimes, two horizontal stresses can be equal to or even greater than the overburden stress. For example, for the subsalt formations not far from the base of salt where three principal stresses are almost equal (\(\sigma_{\text{V}} \approx \sigma_{\text{H}} \approx \sigma_{\text{h}}\)), the formation breakdown pressure can be calculated from Eq. (8) as follows:
Because the pore pressure is less than the overburden stress (\(p < \sigma_{\text{V}}\)), from the above equation we obtain \(P_{\text{b}} > \sigma_{\text{V}}\), i.e., the LOT is greater than the overburden gradient (\({\text{LOT}} > {\text{OBG}}\)). There are many cases where the measured LOT peak values are greater than their overburden stress values in subsalt formations, particularly when the formations are close to the base of salt. Figure 9 shows a case that the measured LOT value is 16.4 ppg at 21,427 ft (342 ft below the base of salt), where the overburden stress gradient is 16.3 ppg, i.e., \({\text{LOT}} > {\text{OBG}}\).
Figure 9 also plots the measured LOT values in the presalt and subsalt formations. There is also a measured FIT value in the salt. The high-side and the most likely fracture gradients in shales calculated from the proposed method [Eq. (16)] are compared to the Matthews and Kelly’s method (with a constant k 0 = 0.75) in Fig. 9. It should be noticed that the sandstone fracture gradient is not plotted in the figure. The most likely (C = 500 psi) and high-case (C = 1000 psi) fracture gradients in salt formation are calculated from Eq. (17) and plotted in the same figure. Figure 9 shows that the proposed methods are better for calculating the fracture gradients.
4 Conclusions
Analysis of more than 200 measured LOT data points in worldwide petroleum basins shows that the effective stress coefficient k 0 has a higher value at the shallower depth and decreases as the depth increases. Based on this phenomenon, a new fracture gradient method using a depth-dependent k 0 is proposed. Case applications show that the proposed method can improve the fracture gradient prediction. For a better predrill prediction, the fracture gradient needs to be calibrated to the offset data, because k 0 may behave differently for different regions.
The LOT and FIT data in salt formations in the Gulf of Mexico are also examined. The results show that the LOT and FIT pressures in most salt formations are larger than the overburden stress. The fracture gradient in salt formation is proposed based on the measured data. The reasons why LOT peak pressures are higher than their overburden stresses are also explained, particularly in the subsalt formations. Case studies are investigated to examine the proposed methods.
References
Aadnoy BS, Larson K. Method for fracture-gradient prediction for vertical and inclined boreholes. SPE Drill Eng. 1989;4(2):99–103. doi:10.2118/16695-PA.
Alberty M, McLean M. A physical model for stress cages. In: SPE annual technical conference and exhibition, 26–29 September, Houston, TX; 2004. doi:10.2118/90493-MS.
Althaus VE. A new model for fracture gradient. J Can Pet Tech. 1997;16(2):99–108. doi:10.2118/77-02-10.
Anderson RA, Ingram DS, Zanier AM. Determining fracture pressure gradients from well logs. J Pet Technol. 1973;25(11):1259–68. doi:10.2118/4135-PA.
Barker JW, Meeks WR. Estimating fracture gradient in Gulf of Mexico deepwater, shallow, massive salt sections. In: SPE annual technical conference and exhibition, 5–8 October, Denver, CO; 2003. doi:10.2118/84552-MS.
Breckels IM, van Eekelen HAM. Relationship between horizontal stress and depth in sedimentary basins. J Pet Technol. 1982;34(9):2191–9. doi:10.2118/10336-PA.
Constant WD, Bourgoyne AT. Fracture-gradient prediction for offshore wells. SPE Drill Eng. 1988;3(2):136–40. doi:10.2118/15105-PA.
Daines SR. The prediction of fracture pressures for wildcat wells. JPT. 1982;34(4):863–72. doi:10.2118/9254-PA.
Detournay E, Cheng AHD. Poroelastic response of a borehole in a non-hydrostatic stress field. Int J Rock Mech Min Sci Geomech. 1988;25(3):171–82. doi:10.1016/0148-9062(88)92299-1.
Eaton BA. Fracture gradient prediction and its application in oilfield operations. JPT. 1969;21(10):25–32. doi:10.2118/2163-PA.
Edwards ST, Bratton TR, Standifird WB. Accidental geomechanics—capturing in situ stress from mud losses encountered while drilling. In: SPE/ISRM rock mechanics conference, 20–23 October, Irving, TX; 2002. doi:10.2118/78205-MS.
Fredrich JT, Engler BP, Smith JA, Onyia EC, Tolman DN. Predrill estimation of subsalt fracture gradient: analysis of the Spa prospect to validate nonlinear finite element stress analyses. In: SPE/IADC drilling conference, 20–22 February, Amsterdam, The Netherlands; 2007. doi:10.2118/105763-MS.
Haimson BC, Fairhurst C. Initiation and extension of hydraulic fractures in rocks. SPE J. 1967;7(3):310–8. doi:10.2118/1710-PA.
Hubbert MK, Willis DG. Mechanics of hydraulic fracturing. Pet Trans AIME. 1957;210:153–68.
Keaney G, Li G, Williams K. Improved fracture gradient methodology understanding the minimum stress in Gulf of Mexico. In: 44th US rock mechanics symposium, 27–30 June 2010, Salt Lake City, UT. ARMA-10-177.
Matthews WR, Kelly J. How to predict formation pressure and fracture gradient. Oil Gas J. 1967;65(8):92–106.
Oriji A, Ogbonna J. A new fracture gradient prediction technique that shows good results in Gulf of Guinea wells. In: Abu Dhabi international petroleum conference and exhibition, 11–14 November, Abu Dhabi, UAE; 2012. doi:10.2118/161209-MS.
Pilkington PE. Fracture gradient estimates in Tertiary basins. Pet Eng Int. 1978;8(5):138–48.
Postler DP. 1997. Pressure integrity test interpretation. In: SPE/IADC drilling conference, 4–6 March, Amsterdam, The Netherlands; 1997. doi:10.2118/37589-MS.
Wessling S, Pei J, Dahl T, Wendt B, Marti S, Stevens J. Calibrating fracture gradients—an example demonstrating possibilities and limitations. In: International petroleum technology conference, 7–9 December, Doha, Qatar; 2009. doi:10.2523/IPTC-13831-MS.
Wojtanowicz AK, Bourgoyne AT, Zhou D, Bender K. Strength and fracture gradients for shallow marine sediments. Final report, US MMS, Herndon; 2000.
Zhang J. Pore pressure prediction from well logs: methods, modifications, and new approaches. Earth Sci Rev. 2011;108(1–2):50–63. doi:10.1016/j.earscirev.2011.06.001.
Zhang J. Borehole stability analysis accounting for anisotropies in drilling to weak bedding planes. Int J Rock Mech Min Sci. 2013;60:160–70. doi:10.1016/j.ijrmms.2012.12.025.
Zhang J, Roegiers JC. Integrating borehole-breakout dimensions, strength criteria, and leak-off test results, to constrain the state of stress across the Chelungpu Fault, Taiwan. Tectonophysics. 2010;492(1–4):295–8. doi:10.1016/j.tecto.2010.04.038.
Zhang J, Wieseneck J. Challenges and surprises of abnormal pore pressure in shale gas formations. In: SPE annual technical conference and exhibition, 30 October–2 November, Denver, CO, USA; 2011. doi:10.2118/145964-MS.
Zhang Y, Zhang J. Lithology-dependent minimum horizontal stress and in situ stress estimate. Tectonophysics. 2017;703–704:1–8. doi:10.1016/j.tecto.2017.03.002.
Zhang J, Alberty M, Blangy JP. A semi-analytical solution for estimating the fracture width in wellbore strengthening applications. In: SPE deepwater drilling and completions conference, 14–15 September, Galveston, TX, USA; 2016. doi:10.2118/180296-MS.
Zhang J, Standifird WB, Lenamond C. Casing ultradeep, ultralong salt sections in deep water: a case study for failure diagnosis and risk mitigation in record-depth well. In: SPE annual technical conference and exhibition, 21–24 September, Denver, CO, USA; 2008. doi:10.2118/114273-MS.
Acknowledgements
This work was partially supported by the Program for Innovative Research Team in the University sponsored by Ministry of Education of China (IRT-17R37), National Key R&D Project (2017YFC0804108) of China during the 13th Five-Year Plan Period, and Natural Science Foundation of Hebei Province of China (D2017508099).
Author information
Authors and Affiliations
Corresponding authors
Additional information
Edited by Yan-Hua Sun
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Zhang, J., Yin, SX. Fracture gradient prediction: an overview and an improved method. Pet. Sci. 14, 720–730 (2017). https://doi.org/10.1007/s12182-017-0182-1
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12182-017-0182-1