1 Introduction

The mechanism of gas flow in nanopores is one of the major focuses in shale reservoir research. The interaction between gas molecules and solid walls becomes so significant that we have to consider this effect on flow mechanisms. There are three types of gas stored in shale reservoirs: free gas (just like the gas in conventional reservoirs), adsorbed gas near the solid wall surfaces and dissolved gas within the organic materials (kerogen). Each type of gas possesses different flow mechanisms. The dissolved gas in kerogen is immovable and structured as the rock solid matrix. When the pressure decreases, dissolved gas will release, leading to the shrinkage of the solid matrix and increment of porosity and permeability. There are lots of studies of this effect in coalbed methane reservoirs, but there are only limited studies for shale and the percentage of dissolved gas is questionable. Etminan et al. (2014) measured the dissolved gas in a shale sample using a pressure decay method and reported that the contribution of dissolved gas (methane) was about 22% of the total gas in place at 4.5 MPa and the adsorbed gas contributed about 38%. Jin and Firoozabadi (2016) adopted the solid-solution model for wax and asphaltene precipitation (Pan and Firoozabadi 1997; Won 1986) to model the gas dissolution in kerogen. The kerogen is believed to be similar to bitumen or solid heavy oil (Mehrabi et al. 2017; Jin and Firoozabadi 2016; Yang et al. 2016). According to Yang et al. (2016), gas dissolves into the organic matter just as natural gas dissolves into heavy oil and gas dissolution in the organic material (kerogen) delays the adsorption process. In Jin and Firoozabadi’s study, the dissolved gas contribution to the total sorbed gas (methane) was approximately 7% at 4.5 MPa (Jin and Firoozabadi 2016), which is much smaller than the value reported by Etminan et al. (2014). They also reported an approximately linear relationship between the dissolved gas volume and pressure. Divided by the total organic content (TOC) values, the normalized dissolved gas volume was obtained and the slopes of the normalized dissolved gas volume with respect to pressure for different samples are the same. Mehrabi et al. (2017) fully reviewed the studies related to dissolved gas and established a model for simulating gas flow in non-circular pores. Their results supported the significance of dissolved gas in shale reservoir production. Heller and Zoback (2014) measured the volumetric swelling strain due to sorption as a function of pressure. In their studies, the volumetric swelling strain is approximately linearly proportional to pressure, especially for methane. All in all, we assume the dissolved gas volume is approximately linearly proportional to pressure, which can be formulated by the Henry equation.

There are many studies of adsorbed gas. Most of those studies neglect the difference between dissolved gas and adsorbed gas and consider both types of gas as adsorbed gas. To make it more accurate, we use sorption referring to the combination of adsorption and dissolution. When we use the Langmuir sorption model, both the adsorbed gas and dissolved gas are considered and they cannot be distinguished in this model. Ambrose et al. (2010) proposed a new model to calculate the gas in place by considering the sorption effect. They believed that the free gas volume needs to be corrected by subtracting the adsorbed layer volume. The sorbed methane layer density was suggested to be 0.34 g/cm3 by molecular dynamic modeling. Pang et al. (2016) experimentally measured the sorption in five shale samples and successfully matched the data using the Dubinin–Astakhov model. The sorption effect on porosity and permeability was carefully studied in their work. Yu et al. (2014) compared the Langmuir and BET models and believed that the increment of sorption at high pressures was caused by multilayer sorption. The BET model was more suitable in their work. A simplified local density model was also successfully used to model the shale adsorption (Chareonsuppanimit et al. 2012; Ma and Jamili 2016). Mostly the sorbed layer is considered immovable and static, but this is not correct. Recently, some scholars modeled the surface diffusion of adsorbed gas and investigated the effect of the adsorbed layer on shale gas flow using analytic models (Wu et al. 2015, 2016a). Molecular dynamic simulation studies have also proven that the adsorbed layer could either enhance or reduce the flow rate in shale reservoirs depending on variations in adsorption under different conditions (Riewchotisakul and Akkutlu 2015; Wang et al. 2016b, c; Wu and Zhang 2016). To our knowledge, the enhancement or reduction of permeability depends on the difference between the surface diffusion capacity of adsorbed gas and the flow capacity of free gas with the corresponding volume fractions.

In summary, dissolved gas is trapped within the rock matrix and is immovable. The adsorbed gas is movable and affects flow velocity. Therefore, we need to model these two different gas states separately.

For free gas, the interaction between gas molecules and the solid wall becomes significant in micro- and nanopores. The smaller the pore size is, the higher frequency of gas–solid collision. In order to characterize the significance of this effect, the Knudsen number was introduced, which refers to the ratio of mean free gas path to the pore size.

$$Kn = \frac{\lambda }{2r}$$
(1)

According to Javadpour et al. (2007), the mean free gas path is expressed as

$$\lambda = \frac{{k_{\text{B}} T}}{{\sqrt 2 \pi d_{\text{m}}^{2} p}}$$
(2)

where \(k_{\text{B}}\), \(p\), \(d_{\text{m}}\) and \(T\) are Boltzmann constant (\(k_{\text{B}} = 1.3805 \times 10^{ - 23}\,{\text{J}}/{\text{K}}\)), gas pressure, gas molecule diameter and temperature, respectively.

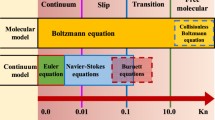
According to the Knudsen number values, different flow regimes are given in Table 1 (Javadpour et al. 2007). For gas flow in shale reservoir conditions, the flow regime is mainly slip flow and transition flow. According to Wu’s study, the Knudsen number is in the range of 0.0002–6 (Wu et al. 2014). So the Darcy equation is not suitable for shale gas reservoirs. There are several proposed apparent gas permeability models, which can be divided into two categories: These are the dusty gas model (DGM) (Javadpour et al. 2007; Javadpour 2009; Darabi et al. 2012; Sakhaee-Pour and Bryant 2012) and Knudsen number-based models (Beskok and Karniadakis 1999; Florence et al. 2007; Civan 2010; Wu et al. 2016b). For the DGM, the Knudsen flow and slip flow are simply added together, which is not appropriate and these should be given some weighting factors (Wu et al. 2016b). For the Knudsen number-based models, most models are mainly based on the BK model (Beskok and Karniadakis 1999) and the coefficients in these models are obtained from the flow in one single micro- or nanotube, which is different from the shale porous media.

Table 1 Flow regimes according to Knudsen number
Full size table

In this work, sorption is modeled by the combination of adsorption and dissolution. We use the Langmuir adsorption equation to represent adsorbed gas and Henry’s equation to represent dissolved gas. A quite reasonable K coefficient is obtained in Henry’s equation. The effect of dissolved gas on porosity and permeability is also discussed. For non-Darcy gas flow, the apparent permeability model for free gas is established by combining the slip flow and Knudsen flow equations. For adsorbed gas, the surface diffusion effect is also considered in this model. Finally, the sensitivity analysis is performed.

2 Sorption

In this work, adsorption is modeled by the Langmuir adsorption equation given by

$$n_{{{\text{a}},{\text{abs}}}} = n_{\text{L}} \frac{p}{{p + p_{\text{L}} }}$$
(3)

where \(n_{{{\text{a}},{\text{abs}}}}\) is the molar number of absolute adsorbed gas; \(n_{\text{L}}\) and \(p_{\text{L}}\) are the Langmuir molar number and the Langmuir pressure, respectively.

Equation (3) describes the absolute adsorption, but only the excessive adsorption can be obtained in the laboratory. So we have revised Eq. (4)

$$n_{{{\text{a}},{\text{ex}}}} = \left( {1 - \frac{{\rho_{\text{f}} }}{{\rho_{\text{a}}^{0} }}} \right)n_{\text{L}} \frac{p}{{p + p_{\text{L}} }}$$
(4)

where \(n_{{{\text{a}},{\text{ex}}}}\) is the molar number of excessive adsorbed gas; \(\rho_{\text{f}}\) is the density of free gas; \(\rho_{\text{a}}^{0}\) is the maximum density of adsorbed gas at high pressures.

For dissolved gas, as mentioned above, we assume the dissolved gas volume is approximately linearly proportional to pressure and the slopes of normalized gas volume (divided by TOC) for different samples are the same. Therefore, we use Henry’s law to describe the dissolved gas

$$n_{{{\text{d}},{\text{abs}}}} = Kp \times {\text{TOC}}$$
(5a)

where \(K\) is the coefficient of Henry’s law; \(n_{{{\text{d}},{\text{abs}}}}\) is the molar number of absolute dissolved gas.

Similar to Eq. (4), we have revised equation Eq. (5b) for Eq. (5a)

$$n_{{{\text{d}}, {\text{ex}}}} = \left( {1 - \frac{{\rho_{\text{f}} }}{{\rho_{\text{d}}^{0} }}} \right)Kp \times {\text{TOC}}$$
(5b)

where \(\rho_{\text{d}}^{0}\) is the dissolved gas density in kerogen; \(n_{{{\text{d}}, {\text{ex}}}}\) is the molar number of excessive dissolved gas.

The total sorption is the sum of adsorption and dissolution, and the new sorption model is given by

$$n_{\text{ex}} = n_{{{\text{a}},{\text{ex}}}} + n_{{{\text{d}},{\text{ex}}}} = \left( {1 - \frac{{\rho_{\text{f}} }}{{\rho_{\text{a}}^{0} }}} \right)n_{\text{L}} \frac{p}{{p + p_{\text{L}} }} + \left( {1 - \frac{{\rho_{\text{f}} }}{{\rho_{\text{d}}^{0} }}} \right)Kp \times {\text{TOC}}$$
(6)

where \(n_{\text{ex}}\) is the molar number of total excessive sorbed gas including adsorption and dissolution.

According to Eq. (6), \(\rho_{\text{a}}^{0}\), \(n_{\text{L}}\), \(p_{\text{L}}\), \(\rho_{\text{d}}^{0}\) and \(K\) are all needed to be determined from the experimental data. \(\rho_{\text{a}}^{0}\) is suggested to be around 0.34 g/cm3 (Ambrose et al. 2010).

The experimental data used here from Pang et al. (2016) are given in Table 2.

Table 2 Shale sample sorption data from Pang et al. (2016)
Full size table

There are five sets of experimental data on methane sorption on shale samples. We apply our new sorption model (Eq. (6)) to fit the experimental data using the least squares method. The same values of \(\rho_{\text{a}}^{0}\), \(\rho_{\text{d}}^{0}\) and \(K\) for all five shale samples are used in this work, and their typical values are chosen and confirmed by matching experimental data from Pang et al. (2016). The sum of the fitting errors for five cores is used as the objective function. Besides, neglecting the difference between solution and adsorption, the general Langmuir model is also applied to these five samples using Eq. (4). MATLAB optimization toolbox is used in this work, and the optimal matching coefficients of Eqs. (4) and (6) are both given in Table 3.

Table 3 Fitting results of both new sorption model and the Langmuir model
Full size table

The corresponding fitting results of each shale sample are given in Fig. 1. We can see from the figures that the new model gives a better match for the experimental data and that the amount of dissolved gas increases almost linearly with respect to pressure. The Langmuir model tends to give an underestimation of the sorption at high pressures. Yu et al. (2014) contended that the increment of sorption at high pressures was caused by multilayer sorption, but we believe it is caused by dissolution. The higher the pressure is, the greater the percentage that the dissolved gas will make up within the overall sorption and the Langmuir sorption model will underestimate the sorption volume. These differences are much larger at high pressures, and the amount of sorbed gas for each shale sample at 30 MPa is shown in Table 4. We can see that only using the Langmuir equation (not considering dissolution) can lead to a significant underestimation of the amount of sorbed gas in shale reservoirs.

Fig. 1
figure 1

Experimental methane sorption data matching results of both the new model and the Langmuir model

Full size image
Table 4 The absolute amount of sorbed gas at 30 MPa using the new model and the Langmuir model
Full size table

As discussed above, the dissolved gas is immovable and dissolved within the solid matrix, while the adsorbed gas is movable and fully coupled with the non-Darcy flow mechanism. These two states of gas are quite different. Dissolution will change the porosity and then permeability as the pressure changes. Considering this effect the porosity is given by

$$\phi = \phi_{0} - \frac{{n_{{{\text{d}},{\text{abs}}}} M}}{{\rho_{\text{d}}^{0} }}\rho_{\text{r}} = \phi_{0} - \frac{KM}{{\rho_{\text{d}}^{0} }}\rho_{\text{r}} p \times {\text{TOC}}$$
(7a)

where \(M\) is the gas molecular weight; \(\phi_{0}\) is the original porosity without dissolution; and \(\rho_{\text{r}}\) is the rock bulk density.

For methane in this work, Eq. (7a) can be expressed as

$$\phi = \phi_{0} - \frac{{0.052 \times 10^{ - 3} \times 16.04}}{1.23}\rho_{\text{r}} p \times {\text{TOC}} = \phi_{0} - 6.78 \times 10^{ - 4} \rho_{\text{r}} p \times {\text{TOC}}$$
(7b)

The permeability change can be expressed as (Pang et al. 2016; Gu and Chalaturnyk 2006)

$$\frac{k}{{k_{0} }} = \left( {\frac{\phi }{{\phi_{0} }}} \right)^{3}$$
(8)

Given \(\phi_{0} = 5\% \;{\text{and}}\;\rho_{\text{r}} = 2.3\; {\text{g}}/{\text{cm}}^{3} ,\) the permeability can be calculated using Eq. (8). The corresponding results are shown in Fig. 2. According to the figure, the permeability decreases as pressure increases for different TOC values. And when TOC is large enough, this effect becomes much more significant. Note that the geomechanical effect is not considered in this work.

Fig. 2
figure 2

Permeability changing due to gas dissolution caused by kerogen swelling

Full size image

3 Non-Darcy gas flow

Because of the nanopores in shale formations, slip flow and transition flow are the main flow regimes of gas flowing in shale reservoirs. Apparent gas models have been reported (Beskok and Karniadakis 1999; Civan 2010; Darabi et al. 2012; Florence et al. 2007; Javadpour et al. 2007; Javadpour 2009; Riewchotisakul and Akkutlu 2015; Sakhaee-Pour and Bryant 2012; Wang et al. 2016a, b, c; Wu et al. 2014, 2015; Wu and Zhang 2016), but these models are mainly based on single nanotube conditions instead of porous media. Moreover, adsorption is closely coupled with the free gas flow in shales.

When \(0.001 < {\textit{Kn}} < 0.1\), at the slip flow regime, the apparent permeability is given by (Beskok and Karniadakis 1999)

$$\frac{{k_{\text{slip}} }}{{k_{\text{D}} }} = 1 + 4\left( {\frac{2}{\sigma } - 1} \right)\frac{\textit{Kn}}{{1 + {\textit{Kn}}}}$$
(9)

where \(k_{\text{slip}}\) is the slip flow apparent permeability; \(k_{\text{D}}\) is the Darcy permeability (intrinsic permeability); \(\sigma\) is the tangential momentum accommodation coefficient (TMAC).

When \({\textit{Kn}} > 10\), the Knudsen flow dominates the flow; the apparent permeability can be expressed as (Wu et al. 2016a, b)

$$\frac{{k_{\textit{Kn}} }}{{k_{\text{D}} }} = \frac{128}{3\pi }{\textit{Kn}}\delta^{{D_{\text{f}} - 2}}$$
(10)

where \(k_{Kn}\) is the Knudsen flow apparent permeability; \(\delta\) is the ratio of gas molecule diameter \(d_{\text{m}}\) to pore diameter \(r\); \(D_{\text{f}}\) is the pore fractal number.

Transition flow is a combination of slip flow and Knudsen flow. So, for all the flow regimes, one general model can be established using the sum of weighted slip and Knudsen flow. This model is formulated by Eq. (11). The weights indicate the percentage of each flow regime. We use the weights from the study of Wu et al. (2016b).

$$\frac{{k_{{{\text{app}}, {\text{free}}}} }}{{k_{\text{D}} }} = \frac{1}{{{\textit{Kn}} + 1}}\frac{{k_{\text{slip}} }}{{k_{\text{D}} }} + \frac{\textit{Kn}}{{1 + {\textit{Kn}}}}\frac{{k_{\textit{Kn}} }}{{k_{\text{D}} }} = \frac{1}{{{\textit{Kn}} + 1}}\left[ {1 + 4\left( {\frac{2}{\sigma } - 1} \right)\frac{\textit{Kn}}{{1 + {\textit{Kn}}}}} \right] + \frac{\textit{Kn}}{{1 + {\textit{Kn}}}}\frac{128}{3\pi }K_{n} \delta^{{D_{\text{f}} - 2}}$$
(11)

Moghaddam and Jamiolahmady (2016) measured the permeability of shale samples and reported the apparent permeability data with respect to the Knudsen number. Fitting the data when \(0.001 < Kn < 0.1\), \(\sigma\) is found to be 0.6 for porous media in their studies.

This permeability model above is only considering the free gas flow in shale. As for adsorbed gas, the mass transfer is

$$J_{\text{surf}} = D_{\text{s}} {\nabla }\rho_{\text{a}}$$
(12)

where \(D_{\text{s}}\) is the surface diffusion coefficient; \(\rho_{\text{a}}\) is the adsorbed gas density, which is changing with pressure, i.e., \(\rho_{\text{a}} = \theta \rho_{\text{a}}^{0}\) and \(\rho_{\text{a}}^{0} = 0.34\; {\text{g}}/{\text{cm}}^{3}\); \(\theta\) is the gas convergence, which is defined as \(\theta = \frac{p}{{p + p_{\text{L}} }}\) when using the Langmuir model.

Surface diffusion coefficient values are still uncertain; however, according to the molecular dynamic simulation results of gas transport in kerogen (Falk et al. 2015), the surface diffusion coefficient is of the same scale of the molecular self-diffusion coefficient. Therefore, the surface diffusion coefficient can be expressed as

$$D_{\text{s}} = \omega \frac{1}{3}\lambda \sqrt {\frac{{8{{RT}}}}{\pi M}} = \omega \frac{{2\mu_{\text{a}} }}{{3\rho_{\text{a}} }}$$
(13)

where \(\rho_{\text{a}}\) and \(\mu_{\text{a}}\) refer to the adsorbed gas density and the corresponding viscosity, which can be calculated using Lee et al.’s method (1966); \(\omega\) is accounting for the difference between self-diffusion and surface diffusion. When the surface diffusivity equals the self-diffusion coefficient, \(\omega = 1\).

When \(\rho_{\text{a}} = \rho_{\text{a}}^{0} = 0.34\, {\text{g}}/{\text{cm}}^{3} , T = 353\, {\text{K}}, \omega = 1,\) from Lee et al.’s method (1966), \(\mu_{\text{a}} = 0.0498\, {\text{cP}}\), then \(D_{\text{s}} = 0.976 \times 10^{ - 7}\, {\text{m}}^{2} /{\text{s}}\), which is close to the value suggested by Wang et al. (2016a).

Applying the definition of permeability for the adsorbed layer, i.e., \(J_{\text{surf}} = \frac{{\rho_{\text{a}} k_{\text{surf}} }}{{\mu_{\text{a}} }}\nabla p\), we can derive the surface diffusion permeability by combining Eqs. (12) and (13) as

$$k_{\text{surf}} = \omega \frac{{2\mu_{\text{a}}^{2} }}{{3\rho_{\text{a}}^{2} }}\frac{{p_{\text{L}} \rho_{\text{a}}^{0} }}{{\left( {p + p_{\text{L}} } \right)^{2} }}$$
(14)

The free gas and adsorbed gas flow relationship can be illustrated in Fig. 3. Combining both flows, the overall apparent permeability can be expressed as

Fig. 3
figure 3

Schematic of free and adsorbed gas flow in nanopores

Full size image
$$k_{\text{app}} = \frac{{\left( {r - \theta d_{\text{m}} } \right)^{2} }}{{r^{2} }}k_{{{\text{app}}, {\text{free}}}} + \frac{{r^{2} - \left( {r - \theta d_{\text{m}} } \right)^{2} }}{{r^{2} }}k_{\text{surf}}$$
(15)

Substituting Eqs. (11) and (14) into Eq. (15) gives the shale gas permeability model

$$k_{\text{app}} = \frac{{\left( {r - \theta d_{\text{m}} } \right)^{2} }}{{r^{2} }}k_{\text{D}} \left\{ {\frac{1}{{{\textit{Kn}} + 1}}\left[ {1 + 4\left( {\frac{2}{\sigma } - 1} \right)\frac{\textit{Kn}}{{1 + {\textit{Kn}}}}} \right] + \frac{\textit{Kn}}{{1 + {\textit{Kn}}}}\frac{128}{3\pi }{\textit{Kn}}\delta^{{D_{\text{f}} - 2}} } \right\} + \frac{{r^{2} - \left( {r - \theta d_{\text{m}} } \right)^{2} }}{{r^{2} }}\omega \frac{{2\mu_{\text{a}}^{2} }}{{3\rho_{\text{a}}^{2} }}\frac{{p_{\text{L}} \rho_{\text{a}}^{0} }}{{\left( {p + p_{\text{L}} } \right)^{2} }}$$
(16)

Darcy permeability can be estimated as

$$k_{\text{D}} = \frac{{r^{2} \phi }}{8\tau }$$
(17)

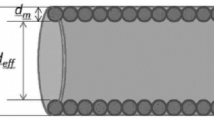
where \(d_{\text{m}}\) is the molecule diameter; \(\tau\) is the tortuosity; \(\phi\) is porosity.

4 Sensitivity analysis for non-Darcy gas flow

According to Eqs. (8) and (16), for the methane flow in shale, given porosity, pore radius, tortuosity, Langmuir pressure and TOC value, the apparent gas permeability can be finally obtained. The basic data are given in Table 5. We use the sorption data of shale sample A-2 from Table 3.

Table 5 Basic data for the sensitivity study
Full size table

Firstly, we only consider the free non-Darcy gas flow using Eq. (11). The results are given in Figs. 4 and 5. When \(\frac{1}{p}\) increases, \(\frac{{k_{\text{app}} }}{{k_{\text{D}} }}\) increases, but the relationship is not linear as the Klinkenberg effect suggested. If we follow the procedure of drawing a straight line to find the Klinkenberg-corrected permeability \(k_{\text{l}}\) to be the Darcy permeability, this value can be either larger or lower than the true Darcy permeability \(k_{\text{D}}\). If the apparent permeability models are concave upward with respect to the Knudsen number (or reciprocal of pressure), then the Klinkenberg-corrected permeability \(k_{\text{l}}\) is lower than the true Darcy permeability \(k_{\text{D}}\). If the apparent permeability models are concave upward, then \(k_{\text{l}} > k_{\text{D}}\). In Fig. 4, specifically, \(k_{\text{l}} < k_{\text{D}}\) for \(r = 30\;{\text{nm}}\) and \(k_{\text{l}} > k_{\text{D}}\) for \(r = \;10\) and 20 nm. This phenomenon explains why there are two types of slip models in the literature. Actually, both types of models are partially correct. If models are more focused on the high Knudsen number regime, then \(k_{\text{l}} < k_{\text{D}}\); if models are more focused on the low Knudsen number regime, then \(k_{\text{l}} > k_{\text{D}}\).

Fig. 4
figure 4

Apparent permeability versus reciprocal of pressure for different pore sizes

Full size image
Fig. 5
figure 5

Apparent permeability versus pressure for different pore sizes

Full size image

Then we consider the adsorption effect (no dissolution, \(p_{\text{L}} = 2.84\;{\text{MPa}}\)) on gas flow in shales applying Eq. (16). With and without adsorption are presented in Fig. 6 for different pore sizes. When the pore radius is larger than 5 nm, the adsorption does not affect the apparent permeability significantly and it is negligible. However, when the pore radius is 2 nm, the apparent permeability is enhanced a lot due to the surface diffusion of adsorbed gas at low pressures. However, the apparent permeability decreases at relatively high pressures, which is similar to the molecular dynamic simulation results (Wu and Zhang 2016).

Fig. 6
figure 6

Apparent permeability for different pore sizes with and without adsorption effect

Full size image

Finally, we combine the gas dissolution kerogen swelling effect with the non-Darcy gas flow. The pore diameter \(r = 10 \,{\text{nm}}\) and TOC = 10% are used in our calculation, and the result is presented in Fig. 7. The dissolution caused permeability reduction is significant at high pressures; the apparent permeability can be lower than the Darcy permeability since the geomechanical effect is not considered in this study.

Fig. 7
figure 7

Apparent permeability versus pressure with and without kerogen swelling effect (pore radius \(r = 10\, {\text{nm}}\) and TOC = 10%)

Full size image

5 Conclusions

In this work, both the sorption and gas non-Darcy flow are carefully studied. From this work, we may draw the following conclusions.

  1. 1.

    The value of K coefficient of 0.052 mmol/(Mpa g TOC) in Henry’s equation is obtained by matching a set of published experimental data, and the value of K coefficient is only related to the properties of kerogen.

  2. 2.

    Using only the Langmuir equation without considering dissolution can lead to a significant underestimation of the amount of sorbed gas in shale reservoirs.

  3. 3.

    The apparent permeability model for free gas is established by combining the slip flow and Knudsen flow equations. As for adsorbed gas, the surface diffusion effect is also considered in this model.

  4. 4.

    When \(\frac{1}{p}\) increases, \(\frac{{k_{\text{app}} }}{{k_{\text{D}} }}\) increases, but the relationship is not linear as the Klinkenberg effect suggested. The effect of adsorption on the gas flow is significant at small pores (\(r \le 2\;{\text{nm}}\)). Adsorption increases gas apparent permeability in shales at low pressures and decreases at high pressures.