1 Introduction

Pipelines have been used as one of the safest ways to transport oil and gas in industry. When the pipelines do not work effectively, a remote-controlled tether-less isolation tool is used in maintenance to isolate high pressure in pipelines and block the fluid without losing the pressure. Understanding of the interaction between the fluid and the isolation tool at different isolation stages is necessary for engineers to design and perform suitable plug operations.

A literature survey has revealed a few papers discussing the interactions between the isolation tool and the fluid in the pipe. Most of the available studies are mechanical designs or have a commercial basis. Tveit and Aleksandersen (2000) introduced a PSI Smart Plug to isolate high pressure in pipelines and risers. Selden (2009) showed a successful application case of a PSI Smart Plug. The isolation tool is developed from a smart Pipeline Inspection Gauge (PIG) and in-pipe robot in engineering. Dynamic analyses of the PIG model under different conditions were carried out (Nieckele et al. 2001; Yeung and Lima 2002; Xu and Gong 2005; Saeidbakhsh et al. 2009; Lesani et al. 2012; Zeng et al. 2014). Minami and Shoham (1995) developed a pigging model and analyzed PIG transient operations, coupling it with the Taitel simplified transient model. Nguyen et al. (2001a, b, c) proposed a computational scheme to estimate the pigging dynamics. Solghar and Davoudian (2012) investigated the transient PIG motion in natural gas pipelines by basic differential forms of the mass and linear momentum equations and validated it using experimental data. Minami and Shoham (1995) developed a dynamic model considering the length of the pig. In in-pipe robot designs, researchers mainly focused on the mechanical design analysis (Minami and Shoham1995; Nguyen et al. 2001a, b, c; Ono and Kato 2004; Wang et al. 2010; Zhao et al. 2010; Vahabi et al. 2011; Solghar and Davoudian 2012; Mirshamsi and Rafeeyan 2012, 2015) and control techniques (Roh et al. 2009; Huang et al. 2010).

The main mechanical parameters influencing the plug process are important for analyzing the interactions between the fluid and the isolation tool. The response surface methodology (RSM) is a statistical and mathematical method which is used in engineering modeling (Han et al. 2012; Saravanakumar et al. 2014; Chen et al. 2015; Li et al. 2015; Poompipatpong and Kengpol 2015; Zhang et al. 2015). Song et al. (2014) conducted an optimal design of the internal flushing channel of a drill bit using the response surface methodology (RSM) and CFD simulation and obtained very good results.

To the best of our knowledge, the modeling effects in the plug process are important for the design of the isolation tool between the geometric transformation and its complicated structure. Moreover, the flow characteristics in a pipe during the plug process are also important for suitable operations of the isolation tool, but those have not been studied. There are also some unanswered questions about interactions between the fluid and the isolation tool, including (1) what is the relationship between the flow characteristics and transforming structures of the plug process in a limited space under turbulent flow conditions; (2) which are the main mechanical parameters of the isolation tool influencing the fluid characteristics in the plug process; (3) how does the flow affect the isolation tool in the plug process.

The aim of this paper is to study the plug process interaction between a transformable isolation tool and the fluid in a pipe and to evaluate the influences of the main mechanical parameters. The plug experiments are conducted using particle image velocimetry (PIV) measurements for estimating interactions in the plug process. The modeling of dynamic characteristics is also conducted from a series of CFD simulations by RSM in the plug process. The influences of the main mechanical parameters are discussed from simulation results.

2 Experimental

In order to visualize the plug process of an isolation tool in pipe flow, a Lucite pipe setup with four models in plug stages was designed. The dimensions of the real isolation tool were relatively big, but the test rig was of limited size. The size of experimental models was scaled down to one-tenth of the real size. The practical Reynolds number, Re was 24,925. Particle image velocimetry (PIV) was used to measure the velocity in the pipe, and the measured velocity results were compared with the results from numerical simulations.

2.1 Physical model of the isolation tool

Figure 1 shows a model of the isolation tool. The isolation tool consists of two pressure heads, a bowl, a plug module, and a cylinder module. Normally, an isolation tool is used to plug the flow in a pipe. The plug operation involves the following steps: The right pressure head drives the plug module until the isolation tool is in the designated position. The plug module rapidly expands along the outside edge of the bowl, causing the outside wall of the plug module to adhere to the inner wall of the pipe. Thus, the plug operation is done without losing the pressure in the pipe.

Fig. 1
figure 1

Physical model of an isolation tool

Full size image

2.2 Geometric deformation of the isolation tool

Figure 2 illustrates two states of the isolation tool experienced. One is the normal state as shown in Fig. 2a. The other is that the plug module is expanded at 99 % (99 % blockage) (see Fig. 2b). Here, d and d 1 are the diameters of the wheel hub and the plug module, respectively. D is the inner diameter of the pipe. The distance from the left boundary to the left end of the isolation tool is L 1. The distance from the right boundary of the pipe to the right end of the isolation tool is L 2. L is the length, while the isolation tool is in the normal state. L p is the length, while the isolation tool is in the blocking state. L d is the length of the isolation tool from the left end of the plug module to the rear end of the isolation tool. This value changes with the expanding percentage increased from 0 (the normal state) to 99 % state. L p1 and L p2 are the lengths from the left boundary to the left end of the isolation tool and from the right boundary to the right end of the isolation tool, respectively. The relationship between the lengths is described by Eq. (1).

$$L_{1} + L + L_{2} = L_{{{\text{p}}1}} + L_{\text{p}} + L_{{{\text{p}}1}}$$
(1)

The normal type and four blockage cases were studied as described in Table 1. The expanding percentages ranged from 0 (the normal state) to the 99 % state. The 100 % blockage state cannot be numerically simulated and tested in experiments.

Fig. 2
figure 2

Deformation models of the isolation tool in a pipe. a Normal state. b Case 5

Full size image
Table 1 Studied cases with L d = 30 mm
Full size table

2.3 The preparation of the test model

For practical experiments, four similar structures of the test models of the isolation tool in water were examined. Four test models were created to understand the effects of the geometric deformation of the isolation tool. The plug modules of the test models were geometrically similar to the physical isolation tool. These four models produced 25 %, 50 %, 75 %, and 99 % blockage (as listed in Table 1). For small changes in the length of the test models, the lengths of L d were all set at 30 mm. The test model with wheels is shown in Fig. 3. The three other types have a similar geometry but a different d 1 values.

Fig. 3
figure 3

Test model isolation tool

Full size image

A PIV was used to record the particle traces in water, using a camera and a double-pulse laser. The data were then input into a computer to calculate the flow features of particles (hollow glass slivered beads with  μm diameter).

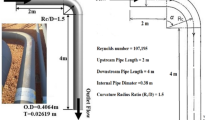
The PIV system is shown in Fig. 4. The pipe in this setup is made of Lucite with an inner diameter of 25 mm. A flow meter was connected to the pipe, and the operating conditions were controlled by the pump. The isolation tool was positioned in the middle of the pipe. To ensure that the flow was fully developed, the lengths of the pipe both before and after the isolation tool were in excess of 2 m. Water containing tracer particles was pumped into the test pipe, and then it flowed into the 100-L water tank. PIV measurements were taken at the symmetry plane, that is, at x = 0. Detailed measurements of the velocity fields were taken using the PIV system (Dantec Dynamics). The plane under investigation was illuminated by a double-pulsed laser. For comparison, numerical simulations were also carried out at the same flow conditions (as shown in Table 2). According to the real condition of the plug stages, the velocity of the isolation tool was slow down to zero and the isolation tool was set at the fixed position with a thin steel line.

Fig. 4
figure 4

Test setup of plug processes

Full size image
Table 2 Test parameters
Full size table

3 Results of PIV experiments

The experiments were carried out at four blockage percentages, namely d 1/D = 0.85 (25 % blockage), d 1/D = 0.9 (50 % blockage), d 1/D = 0.95 (75 % blockage), and d 1/D = 0.99 (99 % blockage). The results are shown in Fig. 5. Each figure consists of a geometric graph (sizes are in mm), images captured by a camera installed outside the experimental pipe, and 2D velocity vectors measured by the PIV. The region measured with the PIV (the section indicated by the red square) approximates to the centerline downstream near the bottom of the test model.

Fig. 5
figure 5

Experimental velocity vectors for increasing degrees of blockage at the vertical yz plane. a 25 % blockage. b 50 % blockage. c 75 % blockage. d 99 % blockage

Full size image

The velocity of fluid particles around the test model in the pipe varied considerably and increased from 25 % blockage stage to 99 % blockage stage, as shown in Fig. 5. In Fig. 5, 2D velocity vectors illustrate the flow pattern downstream of the test model as the blockage percentage increased at the symmetry plane. The section indicated by the red square is where the PIV measurements were conducted. For 99 % blockage (Fig. 5d), the velocities of the most of fluid particles in the measurement section decreased significantly and the recirculation structure and flow pattern disappeared. As the graph shows, the length of the vectors represents the velocity, which falls from 25 % blockage stage to 99 % blockage stage. The velocity value was the smallest in the case of 99 % blockage because the flow was almost completely stopped. As proposed by Oztop et al. (2012) for turbulent flow over a double forward-facing step with obstacles, an increase in the step height produced the same distribution of the velocity vector with an increase in the blockage percentage.

As the blockage percentage changed, the recirculation structure and flow pattern varied as well. To analyze the effect of the geometry deformation in the flow field downstream, the velocities along the centerline for different blockage types were obtained from numerical simulations. The mean values of the obtained experimental data are also shown in Fig. 6. Given the limitations of the experiment, the velocity profile at the centerline could only be obtained at the position from z = 0.04 m to z = 0.044 m. The values of the velocities show the variation in the obstructed flow for different blockage percentages. At the beginning of the transformation, the velocities dropped quickly. The flow velocities changed rapidly as the transformable isolation tool applied 25 % blockage and 75 % blockage. Furthermore, the velocities became steady at approximately 0.04 m s−1 in the 99 % blockage state. Due to the measured data only focusing on a small section, it is basically impossible to consider the main velocity tendency of the flow. A numerical simulation was conducted under experimental conditions, and the characteristics of the flow at different plug processes would be studied for the entire area. From the verification given by Fig. 6, the simulation results can be used to study the effects of the plug process in greater depth.

Fig. 6
figure 6

Experimental and simulated velocities along the z direction at different degrees of blockage

Full size image

4 Interaction between the fluid and the isolation tool in the plug process

As mentioned before, the experimental tests had limitations and the numerical simulation was presented to study the interaction between the fluid and the deformable isolation tool in the plug process. The standard k-ε turbulence model was used with Fluent software for the simulation.

4.1 Computational models

The governing equations of mass conservation [Eq. (2)] for fluid flow are described below. In the numerical simulation model, it is assumed that the fluid is fully developed and incompressible under turbulent conditions and no heat transfer occurs. The numerical method is based on the time-marching version of the semi-implicit method for pressure-linked equations consistent (SIMPLEC).

$$\frac{\partial \rho }{\partial t} + \frac{\partial (\rho u)}{\partial x} + \frac{\partial (\rho v)}{\partial y} + \frac{\partial (\rho w)}{\partial z} = 0$$
(2)

where ρ is the fluid density, kg m−3; u is the fluid velocity in the x direction, m s−1; v is the fluid velocity in the y direction, m s−1; w is the fluid velocity in the z direction, m s−1.

The features of the flow field through the isolation tool are as follows: the single phase flow is incompressible, and the fluid velocity is low. Equation (3) depicts the turbulence kinetic energy k, and the equation for the turbulence dissipation rate ε is given as Eq. (4).

$$\rho \frac{\partial k}{\partial t} + \rho v\frac{\partial k}{\partial y} = \frac{\partial }{\partial y}\left[ {\left( {\eta + \frac{{\eta_{t} }}{{\sigma_{k} }}} \right)\frac{\partial k}{\partial y}} \right] + \eta_{t} \frac{\partial u}{\partial y}\left( {\frac{\partial u}{\partial y} + \frac{\partial v}{\partial y}} \right) - \rho \varepsilon$$
(3)
$$\rho \frac{\partial \varepsilon }{\partial t} + \rho w\frac{\partial k}{\partial z} = \frac{\partial }{\partial z}\left[ {\left( {\eta + \frac{{\eta_{t} }}{{\sigma_{k} }}} \right)\frac{\partial \varepsilon }{\partial y}} \right] + \frac{{c_{1} \varepsilon }}{k}\eta_{t} \frac{\partial u}{\partial y}\left( {\frac{\partial u}{\partial y} + \frac{\partial v}{\partial y}} \right) - c_{2} \rho \frac{{\varepsilon^{2} }}{k}$$
(4)

where k is the turbulent kinetic energy, m2 s−1; η is the dynamic viscosity, kg (s m)−1; η t is the turbulence viscosity, \(\eta_{\text{t}} = c_{\mu } \rho \frac{{k^{2} }}{\varepsilon }\), kg (s m)−1; ε is the turbulence dissipation rate, m2 s−1; c 1 and c 2 are the turbulent dissipation rate coefficients, \(c_{1} = 1.44\), \(c_{2} = 1.92\); and the model constants \(c_{\mu } = 0.09\).

4.2 Boundary conditions

To improve the efficiency of calculation, three-dimensional mesh models of the isolation tool and pipe were created, as shown in Fig. 7. A no-slip condition at the pipe walls was assumed. There are ten rows in the boundary condition of the structure of the isolation tool. The mesh areas of the inlet face consisted of triangular cells. A tetrahedral mesh type was applied to the overall model. The whole grid system had 463,904 cells and 89,035 nodes and can be simulated accurately and display clearly. The meshing process was conducted more densely from the boundary of the isolation tool to the flow field. The three-dimensional mesh model and the inlet face are shown in Fig. 7.

Fig. 7
figure 7

Mesh model. a Three-dimensional mesh models of the isolation tool and the pipe. b Mesh between the isolation tool and the wall. c Mesh model of the inlet face A–A

Full size image

4.3 Box–Behnken simulation design

The Box–Behnken design is a response surface methodology design, and it is effective to identify regression model coefficients. In each block, a number of factors are put through all combinations for the factorial design, while the other factors are kept at the central values. Wu et al. (2012) conducted an optimal design for the foam cup molding process with the Box–Behnken design and obtained very good results. In this study, three factors are selected to evaluate their influences on the pressure drop between upstream and downstream of the isolation tool. Leontini and Thompson (2013) discussed the geometrical effects, and it is important to study the effects of the length (L), diameter of the plug module (d 1), and the diameter of the pressure head (d). Three factors were influential parameters, and the level three was selected as shown in Table 3. Then, the 3-factor Box–Behnken design coordinates are listed in Table 4.

Table 3 Level of design factors
Full size table
Table 4 Design layout and corresponding responses
Full size table

CFD simulations were conducted using the experimental design. The results for the pressure drop over the isolation tool, Δp, are listed in Table 4. The resulting design combinations are also listed in Table 4.

4.4 Numerical results

4.4.1 Validation of the numerical model

The model was validated by the normalized axial velocity profiles from previous research (Camussi et al. 2008). Computations were performed for Reynolds number Re = 8800. In Fig. 8, the normalized velocity profile is in a good agreement with PIV results of Camussi et al. (2008), where w/w 0 is the velocity ratio profiles and y/h is a position to downstream of the step (w is the fluid velocity in the z direction; w 0 is the inlet velocity; y is coordinate in the y axis; h is the height of step).

Fig. 8
figure 8

A comparison of the velocity profile obtained by Camussi et al. (2008) with the simulated velocity profile

Full size image

4.4.2 Effects on velocities between flow and the isolation tool in the plug process

Figure 6 shows the centerline velocity of flow for each degree of blockage. The velocity was measured at the symmetry plane, and the plots show both the experimental values (symbols) and numerical data (symbol lines). The upstream velocity of the test model appears to be steady state and remains almost the same regardless of the degree of blockage, approximating to the inlet velocity. However, the downstream velocity changes rapidly as the degree of blockage changes and a significant change appears at the rear end of the model. The peak flow velocity increases with an increase in the degree of blockage. The same phenomenon was found at high Reynolds numbers (Yoshioka et al. 2001) in flow over backward-facing steps. The velocity changes considerably in the region near the rear face of the model, leading to recirculation.

The velocity of the fluid between the model and the wall (as shown in Fig. 9) reached a maximum value when the blockage percentage approached 75 %. Subsequently, the velocity dropped quickly when the degree of backflow recirculation reached 50 % blockage. The experimental data exhibited the same trend as the simulation results, thus confirming the existence of low velocities and the appearance of recirculation around the isolation tool. Subsequently, the velocity behind the isolation tool became steady without any large fluctuations downstream.

Fig. 9
figure 9

Numerical streamlines along the pipe wall for increasing degrees of blockage in the vertical yz plane

Full size image

To understand the behavior of the velocity of flow through the isolation tool and the effects of the deformation of the isolation tool, Fig. 10 presents transverse velocity profiles at the upstream location (x = 0, z = −0.032 m), the symmetry plane (x = 0, z = 0 m), and the downstream location (x = 0, z = 0.032 m). Figure 10a shows the velocity profiles at the upstream location for four degrees of blockage. The velocity in this figure is in a good agreement with previous observations in which the upstream velocity is steady for each degree of blockage, being almost the same as the inlet velocity. In the region near the wall, however, the velocity fluctuates slightly, indicating the effect of the deformation of the isolation tool. Then, for the symmetry profile (x = 0, z = 0) (shown in Fig. 10b), the velocity is higher near the pipe wall because the pressure drop increases rapidly with the degree of blockage. For 75 % blockage, the velocity is the highest in this region. The pressure in this region increases due to the deformation of the isolation tool, so the flow velocity increases sharply. When the degree of blockage is 99 %, the velocity is zero in this region as few particles are detected in the fluid. Figure 10c shows that the velocity downstream begins to fluctuate and recirculation appears. In the downstream section, the velocity near the wall increases with the degree of deformation, with the velocity peaking for the 75 % blockage. The flow velocity decreases near the pipe wall for the 99 % blockage, and the deformation of the isolation tool has almost completely obstructed the pipe. The fluctuation around the centerline changed remarkably, however. The peak velocity of recirculation exhibits asymmetry, together with an upward trend (as shown in Fig. 10d).

Fig. 10
figure 10

Velocities of fluid particles in different planes. a Upstream velocity in the plane (x = 0, z = −0.032 m). b Velocity of the flow between the plug module and the pipe wall in the plane (x = 0, z = 0 m). c Downstream velocity in the plane (x = 0, z = 0.032 m). d Peak recirculation velocity under different conditions in the plane (z = 0.032 m)

Full size image

4.4.3 Interaction model and analysis of main mechanical parameters

Figure 11 shows the pressure contour on the isolation tool from 0 (normal state) to 99 % blockage. It can be seen that the left pressure head experiences the highest pressure and the pressure applied on the plug module is not so high. The pressure applied on the right pressure head is low, but most of the modules, except for the wheel and the wheel hub, are exhibited in a high negative pressure. A negative pressure is created by the complicated structure and a sudden expansion of flow which is not obstructed by the rear end of the isolation tool. To better understand the pressure variation with the geometric transformation, the pressures at the centerline and along the pipe wall are shown in Fig. 12, respectively. Figure 12a shows that all of the upstream pressures are higher than those downstream. The upstream pressure increases with the degree of blockage, especially between 75 % and 99 % blockage. The upstream and downstream pressures are stable and do not fluctuate. The pressures along the pipe wall (Fig. 12b) are different from the pressures shown in Fig. 12a in terms of the isolation tool location. It can be seen that only a small amount of fluctuation appears as the degree of blockage increases. Table 5 shows the pressure drop between the upstream and downstream areas at the centerline and along the pipe wall. The pressure drop at the centerline is higher than that along the pipe wall. The pressure difference is computed in Table 5. This shows that the pressure difference is not linear with the blockage increasing and the highest is 17,783 Pa for the 75 % blockage stages, rather than for the 99 % blockage.

Fig. 11
figure 11

Pressure contours on the isolation tool. a Normal condition. b 25 % blockage. c 50 % blockage. d 75 % blockage. e 99 % blockage

Full size image
Fig. 12
figure 12

Pressure distribution along different positions with increasing blockage percentages in the vertical yz plane. a Pressure at the centerline. b Pressure along the pipe wall

Full size image
Table 5 Pressure drop and difference
Full size table

Analysis of variance (ANOVA) and response surface analysis were used to determine the statistical significance of the model. The adequacy of the model was predicted with the ANOVA (P < 0.05) and regression analysis (R 2). The relationship between the response and independent variables was demonstrated using a response surface plot.

The second-order regression model of Δp is shown in Eq. (5), and estimated regression coefficients are listed in Table 6.

$$\begin{aligned} \Delta p & = b_{0} + b_{1} L + b_{2} d_{1} + b_{3} d + b_{4} L^{2} + b_{5} d_{1}^{2} + b_{6} d^{2} + b_{7} (Ld) \\ & \quad + b_{8} (Ld_{1} ) + b_{9} (dd_{1} ) + b_{10} (L^{2} d_{1} ) + b_{11} (d_{1}^{2} d) \\ \end{aligned}$$
(5)
Table 6 Estimated regression coefficients
Full size table

The result of ANOVA (Table 7) reveals the relationships between mechanical parameters and the pressure drop Δp over the isolation tool. The indices in Table 7 illustrate the sum of squares, mean squares, the degrees of freedom (DF), F value, and probability (p value), as well as the percentage contribution (C). The low p value indicates that the regression model can predict Δp from the designed factors with 99.88 % confidence. It is clear that d 1 greatly influences Δp which has 10.78 % of the contribution from the results of ANOVA. The parameter d has a contribution of 3.76 %. The parameter L has a minimum influence among the single parameters with 0.12 % contributions. The coupling terms like BC(d 1 d), B2(d 21 ), A2B(L 2 d 1) are dominant 27.35 %, 27.44 %, and 13.22 % with contributions. Three-dimensional surface plots between Δp and three parameters are shown in Fig. 13 with help of the Minitab software package. Figure 13 shows the surface plots of the pressure drop Δp against two variable factors and one fixed variable. In Fig. 13a, the fixed variable d 1 was held at the minimum value. The surface plot shows that the pressure drop Δp increases with the values of d. The value L becomes greater, and the pressure drop Δp shows nonlinear relations with it. In Fig. 13b, the fixed variable d was held at the minimum value. The surface plot shows that the greater the values of d 1, the greater the pressure drop Δp is. The value L becomes greater, and the pressure drop Δp shows nonlinear relations with it. In Fig. 13c, the fixed variable L was held at the middle value. The surface plot shows that the greater the values of d 1 and d, the greater the pressure drop Δp is.

Table 7 ANOVA table for Δp
Full size table
Fig. 13
figure 13

Surface plots between the pressure drop Δp and three parameters. a d and L with d 1 = 22.38 mm. b d 1 and L with d = 22 mm. c d 1 and d with L = 40 mm

Full size image

5 Conclusions

In this study, interactions between the turbulent flow and the isolation tool in the blocking process were investigated with experimental tests and numerical simulations. A comparison between the experimental results and numerical simulation indicates that the standard k-ε model can be used to predict the flow characteristics in the plug process. The influences of the main mechanical parameters were evaluated, and the regression model can be used to predict the relationships between the pressure drop (Δp) and the three main mechanical parameters of the isolation tool in the plug process. The major results can be summarized as follows:

  1. (1)

    The downstream pressure and velocity changed more rapidly than those upstream, while the pressure drop (Δp) changed considerably.

  2. (2)

    The pressure drop was found to change as the degree of blockage increased, with the variation being the greatest for 75 % blockage. The regression model between the pressure drop and mechanical main parameters was obtained.

  3. (3)

    The diameter d 1 greatly influences Δp which has 10.78 % of the contribution and the parameter d has a contribution of 3.76 %. The parameter L has a minimum influence among the single parameters with 0.12 % contribution.

Note that this study provides the way to analyze the interactions between the flow and the isolation tool in the plug process, and the regression model was built to evaluate the influences of the main parameters. It is pointed that the plug process of the isolation tool is a slow dynamic process. Further study will focus on the transient plug process of the isolation tool in numerical simulations and experimental tests.