1 Introduction

In gas–solid circulating fluidized (CFB) beds, the particles are collected by cyclones and then returned into a fluidized bed along a cyclone dipleg (dip-leg) conveying system. In the cyclone dipleg, the particles are conveyed mainly under gravity action from a low-pressure top section to a high-pressure bottom region in which the flow behavior is different from that in the riser or in the downcomer, although they have the same tubular structure. One of the flow characteristics in the dipleg is that the particle velocity is greater than gas velocity, so the direction of slip velocity between gas and particles is upward. Another one is the particle flow is usually against a negative pressure gradient. These two characteristics lead to the complexity of fluidization pattern and flow instability in the dipleg, which demonstrates that there are more than one different fluidization pattern coexisting and distinctive pressure fluctuations in the dipleg (Kunni and Levenspiel 1991; Hoffmann and Stein 2002; Cortés and Gil 2007).

Many researchers have studied diplegs, including Geldart et al. (1993), Li et al. (1997), Wang et al. (2000a,b), and Gil et al. (2002). Their emphases were focused on measuring the axial pressure distribution along the dipleg axial height and the fluidization regime transitions in the dipleg. Wang et al. (2000a,b) and Leung and Wilson (1973) investigated the gas-particle flow instability in the dipleg, and the effect of particle mass flux and negative pressure on the instability. Srivastava et al. (1998) and Zhang et al. (1998) found that under certain operating conditions the particle circuit manifested instability characterized by low frequency oscillations of particle circulation rates, and this instability originated in the standpipe. However, little work has been done on gas-particle flow instability involving the cyclone dipleg; furthermore, the relationship between the pressure fluctuations and the fluidization regime transitions, and the effect particle mass flux on the pressure fluctuations, is rarely reported.

In this work, a series of experiments were conducted with a catalyst powder in a pilot-plant scale CFB unit, to examine the pressure behavior in a 150-mm inner diameter (i.d.) and 9000-mm height cyclone dipleg under a wide range of operating conditions. The time mean pressure and the time series of pressure fluctuations in the cyclone dipleg are discussed based on the measured pressure data. In addition, the pressure fluctuation mechanism was also studied.

2 Experimental

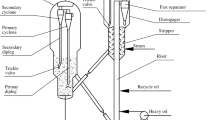
Figure 1 shows the experimental setup employed in this work. It mainly consists of a fluidized bed (600 mm i.d. and 8000 mm height), a riser (200 mm i.d. and 12,500 mm height), and a dipleg (150 mm i.d. and 9000 mm height) connected with a cyclone. The cyclone has a cylinder with 400 mm i.d. The dipleg is made of plexiglas, making it easy to observe the internal flow phenomena. The dipleg exit was dipped into a dense bubbling fluidization bed without any valve. Particles separated from the cyclone flowed into the dipleg and then discharged into the fluidized bed at the bottom exit of the dipleg. After the particles were conveyed back into the fluidized bed, the particles were pneumatically transported upward by gas through the riser and into the cyclone for separation again. The dipleg was equipped with a set of pressure transducers along its axial height for measuring pressure (as shown in Fig. 1). The measuring range of each pressure transducer was chosen based on the expected maximum pressure at each measure point. The accuracy of the pressure transducer was within ±0.5 %. All signals from the pressure transducer were recorded simultaneously for a 30-s length of time. The axial base point (Z = 0) was set at the inlet of the dipleg, and the positive direction of axis Z is upward as shown in Fig. 1. The particle mass flux was measured by diverting the particles flowing into a collection vessel (not drawn in Fig. 1) for a known period and recording the mass accumulated in that vessel. The particle mass flux was controlled by a valve in the inclined pipe. The superficial gas velocity in the fluidized bed was 0.17–0.18 m s−1. The solid particles employed in the experiments were equilibrium fluid catalytic cracking (FCC) catalyst powders, which had a bulk density of 1030 kg m−3, a particle density of 1560 kg m−3, and a Sauter mean diameter of 63.6 μm. The particle size distribution of FCC catalysts is displayed in Fig. 2.

Fig. 1
figure 1

Schematic diagram of the experimental setup and its photo (non-operating status)

Full size image
Fig. 2
figure 2

Particle size distribution of FCC catalysts

Full size image

3 Results and discussion

3.1 Flow phenomena in the dipleg

While the gas-particles flowed steadily in the dipleg under the designed operating conditions, the fluidization regime could be identified by visual observation. Based on the experimental phenomena, the fluidization regimes in the dipleg can be divided into two types, namely the dilute–dense coexisting falling flow and the dense conveying flow. In the dilute–dense coexisting falling flow, the dilute phase region is composed of a length of swirling flow below the inlet of dipleg and a dilute falling flow above the dense bed level. For example, when particle mass flux G s was small (such as G s < 50.0 kg m−2 s−1), from the top section to the bottom section of the dipleg, the swirling flow, the dilute falling flow, and the dense flow appeared in the dipleg, respectively, as shown in Fig. 3a, b. The swirling flow was just located below the cyclone bottom and showed a helical particle flow along the wall of the dipleg. As the particles moved down, the swirling flow gradually straightened with the particles spreading over-section and forming the dilute falling flow mode. It was observed that the particles looked like heavy rain through the dipleg. At the bottom of the dipleg, the dense flow resembled a bubbling fluidized bed. There were some gas bubbles rising in the dense bed, which was the fluidized gas bypassing from the exit of the dipleg. So the particle phase moved downward and gas phase moved upward in the dense bed flow regime. With increasing G s, the particle concentration in the dilute falling flow region increased, and the existing regions of swirling flow and dense flow reduced. The interface between the dilute falling flow and the dense flow moved up and down unsteadily caused by the eruption of rising gas bubbles. While G s = 200.0–250.0 kg m−2 s−1, the interface disappeared, and there were no gas bubbles in the dipleg. The fluidization regime was transferred from the coexistence of a dilute phase and dense phase flow to the dense conveying flow, as shown in Fig. 3c. Further increasing G s (such as G s > 350.0 kg m−2 s−1), the fluidization regime became the dense conveying flow with a high particle concentration, as shown in Fig. 3d. The gas phase from the cyclone was carried by particles moving downwards. The particle flowing process showed the pressure fluctuation characteristics within the whole dipleg, and the particle concentration distribution looked like a bamboo joint type near the bottom of the dipleg. Figure 4 shows the photos of fluidization regimes in the dipleg during operation. Figure 4a shows the coexistence of dilute falling flow and dense flow, and Fig. 4b shows the dense conveying flow.

Fig. 3
figure 3

Diagram of fluidization regimes in the dipleg

Full size image
Fig. 4
figure 4

Photos of fluidization regimes in the dipleg. a Dilute falling flow and dense flow. b Dense conveying flow

Full size image

3.2 Time mean pressure profiles in the dipleg

For this submerged dipleg, the typical time mean pressure profiles along the axial direction were characterized by a progressively increasing pressure from top to bottom, as shown in Fig. 5. The time mean pressure profiles could be divided into three regions according to the local pressure gradient or the linear pressure distribution. The region I (swirling flow) was just below the inlet of dipleg, where the pressure gradient was small or even zero due to an annular flow. The region II (dilute falling flow) was observed at the top section of the dipleg and showed an intermediate pressure gradient, which varied with increasing particle mass flux. The region III (dense flow) appeared at the bottom of dipleg and displayed a large pressure gradient. The pressure gradient in region III decreased with increasing particle mass flux. In addition, the exit pressure of the dipleg increased considerably with increasing particle mass flux.

Fig. 5
figure 5

Time mean pressure profiles along the axial height of the dipleg

Full size image

The pressure profiles are essentially similar to those obtained by Geldart et al. (1993), Li et al. (1997), and Wang et al. (2000a). However, the dipleg employed in this work has a larger diameter and longer length than those used in others’ research. Furthermore, the exit of dipleg was submerged deeply into the bubbling fluidized bed in this work. So while the particle mass flux was increasing, the whole shape of pressure profile gradually became smooth, and the pressure difference between the dipleg inlet at its top and dipleg outlet at its bottom increased. Consequently, the pressure buildup range for balancing the negative pressure extended from the just dense flow pattern region in the lower region to the whole dipleg length, forming the dense conveying flow regime as shown in Fig. 5.

The relationship between pressure and axial position can be used to calculate the apparent voidage \(\varepsilon\) in the dipleg if the wall friction and acceleration action of particles are neglected, as shown in the following equation:

$$\Delta P = g(1 - \varepsilon )\rho_{\text{s}} \Delta Z\,{\text{or}}\,\varepsilon = 1 - \frac{1}{{\rho_{\text{s}} g}}\frac{\Delta P}{\Delta Z},$$
(1)

where \(\Delta P\) and \(\Delta Z\) are the pressure difference and axial coordinate difference between two pressure transducers, respectively. So, the corresponding voidage profiles in the dipleg are obtained according to the interval pressures. Figure 6 shows that the apparent voidage decreased continuously with particle flowing downwards in the dipleg, in accordance with the description for a downcomer given by Li et al. (1997). Figure 6 also demonstrates that the voidage in most parts of the dipleg decreased with increasing particle mass flux except in the bottom region of the dipleg. As a result, the voidage distribution tended to uniformity with increasing particle mass flux.

Fig. 6
figure 6

Voidage profiles in the dipleg

Full size image

On the other hand, the particle velocity can be obtained by means of the following continuity equation with known G s and \(\varepsilon\):

$$V_{\text{s}} = \frac{{G_{\text{s}} }}{{\rho_{\text{s}} (1 - \varepsilon )}}.$$
(2)

The cross-sectional particle velocity obtained showed that the velocity was gradually decreasing along the particle flow direction in the dipleg, where the particles flow downward from the low-pressure top region to the high-pressure bottom region. Such phenomenon was not observed in the downcomer. Moreover, since the particle velocity was related to the particle mass flux and the voidage, the particle velocity increased with increasing particle mass flux.

3.3 Pressure fluctuation

The experimental results indicated that the gas-particle flow was instable in the dipleg. This instable gas-particle flow can be expressed in the form of pressure fluctuation. Figure 7 shows the pressure profiles with time measured along the dipleg. The time mean values of these dynamic pressures are shown in Fig. 5. The dynamic pressure profiles in Fig. 7 consist of two different types of pressure fluctuations: one is of low frequency and high amplitude and another is of high frequency and low amplitude.

Fig. 7
figure 7

Pressure fluctuation profiles in the dipleg. a G s = 50.0 kg m−2 s−1, b G s = 198.0 kg m−2 s−1, c G s = 385.0 kg m−2 s−1

Full size image

The pressure fluctuations were related to the particle mass flux and fluidization pattern inside the dipleg. When G s was small (such as G s < 50.0 kg m−2 s−1), the pressure fluctuation in Fig. 7a was of high frequency and low amplitude in the dilute falling flow, and low frequency and high amplitude in the dense flow. The former was caused by the falling particle clusters interacting with the up flowing gas, and the latter was caused by the bubbles rising in the dense flow. As G s increased, the particles had a greater tendency to increase the population of clusters rather than to increase the cluster size, resulting in the pressure fluctuation with high frequency and low amplitude, as shown in Fig. 7b. However, the particle feed from the cyclone into the dipleg showed considerable instability, which caused the pressure fluctuation with low frequency and high amplitude. Meanwhile, the surface of the dense flow moved up and down unsteadily, showing significant pressure fluctuations with low frequency and high amplitude. When G s increased (such as G s > 350.0 kg m−2 s−1) to form dense conveying flow, the pressure fluctuations are shown in Fig. 7c. The down-flowing clusters of particles fall inside the dipleg, and as a result, quantities of gas were carried downwards by the particles, which has been proven by the measured results of Geldart et al. (1993) and Li et al. (1997). Gas-particle flow in the dipleg was flowing against negative pressure, and the slip velocity was upward to balance the negative pressure, resulting in compression of the carried gas. The gas was compressed and expanded alternately to induce the particle concentration and the pressure non-uniformity. Therefore, the pressure fluctuations are attributed to the unstable feed and the compressed gas.

Furthermore, the transfer direction of pressure fluctuations can be identified according to the similarity of pressure profiles, as shown in Fig. 7. The particles in the dipleg were essentially free flowing with the help of gravity, but gas was dependent on the particle flow. The pressure fluctuation propagated downward in the fluidization pattern of dilute falling flow and dense conveying flow, and upward in the fluidization pattern of dense flow.

3.4 Standard deviation of the pressure fluctuations

Because the amplitude of the pressure fluctuation is related to the particle mass flux in the dipleg, the pressure fluctuations can reflect the fluidization regimes of the particle transport types. The pressure fluctuation intensity can be described by the standard deviation of fluctuation pressure. Figure 8 shows the standard deviation profiles of pressure fluctuations along the dipleg under different particle mass fluxes. The pressure fluctuations are attributed to many factors in the operation of diplegs, including particle clusters, gas bubbles, wall friction, and instability of feed and discharge, which enable the pressure fluctuations to be multi-scale and complex in nature (Bi 2007; Jing and Li 1999).

Fig. 8
figure 8

Standard deviation of pressure fluctuations in the dipleg

Full size image

When G s was small (such as G s < 50.0 kg m−2 s−1), the fluidization pattern in the dipleg was featured by the coexistence of dilute falling flow and dense flow. In the upper dilute region, the pressure fluctuations originated from the particle clusters flowing downwards and the unstable feed from the cyclone. While in the bottom dense region, the local pressure fluctuations originated from the local bubbles and unstable discharge. With increasing G s, the particle concentration increased. The pressure fluctuation mainly resulted from the unstable feed, the friction between particles and wall, the gas compressed by particles, etc. The pressure fluctuation intensity reached a maximum during the fluidization pattern being transformed (while G s = 200.0–250.0 kg m−2 s−1). With further increase of G s (such as G s > 350.0 kg m−2 s−1), the gas-particle flow evolved into dense conveying flow. The amplitude of the pressure fluctuations gradually decreased. The reason is that the increasing particle mass flux can reduce the possibilities of forming a non-uniform distribution of particle concentration and causing pressure fluctuations. It was clear that the influence of gas turbulence was weakened and the interaction between particles or clusters was dominant as particle flux increasing. The continuous agglomeration of particles and the crush of clusters led to the fluctuation of dynamic pressure.

As discussed above, the interaction and the coupling among gas-particle flow and unstable feed created the complexity of local pressure fluctuations. On the other hand, the pressure fluctuations could produce an alternating load to induce the vibration of the cyclone and dipleg. Sometimes the alternating load could induce resonance vibration of the cyclone system and possibly cause a fatigue fracture of the cyclone shell or support rod (Zheng et al. 2011). So, the pressure fluctuation in the dipleg has the potential harm to the operation of the cyclone system.

4 Conclusions

This paper presents an experimental study on the pressure behaviors of a catalyst powder flowing down in a dipleg with 150 mm i.d. and 9000 mm high. The experimental phenomena displayed that the fluidization regimes in the dipleg could be divided into two types on the whole: the dilute–dense coexisting falling flow and the dense conveying flow. In the dilute–dense coexisting falling flow, the dilute phase region was composed of a length of swirling flow below the inlet of dipleg and a dilute falling flow above the dense bed level. As particle mass flux increased, the fluidization regimes gradually developed into dense conveying flow. Meanwhile, the time mean pressure increased progressively. The time series of pressure fluctuations showed that there existed a gas-particle flow instability in the dipleg, which consisted of low frequency with high amplitude and high frequency with low amplitude. The former was caused by the falling particle clusters, the latter was the result of the other factors, such as bubbles rising in the dense flow, instability feed, and compressed gas. The results indicated that the particle mass flux had strongly influence on the time mean pressure and pressure fluctuations.