Abstract
The velocity profiles and separation efficiency curves of a hydrocyclone were predicted by an Euler–Euler approach using a computational fluid dynamics tool ANSYS-CFX 14.5. The Euler–Euler approach is capable of considering the particle–particle interactions and is appropriate for highly laden liquid–solid mixtures. Predicted results were compared and validated with experimental results and showed a considerably good agreement. An increase in the particle cut size with increasing solid concentration of the inlet mixture flow was observed and discussed. In addition to this, the erosion on hydrocyclone walls constructed from stainless steel 410, eroded by sand particles (mainly SiO2), was predicted with the Euler–Lagrange approach. In this approach, the abrasive solid particles were traced in a Lagrangian reference frame as discrete particles. The increases in the input flow velocity, solid concentration, and the particle size have increased the erosion at the upper part of the cylindrical body of the hydrocyclone, where the tangential inlet flow enters the hydrocyclone. The erosion density in the area between the cylindrical to conical body area, in comparison to other parts of the hydrocyclone, also increased considerably. Moreover, it was observed that an increase in the particle shape factor from 0.1 to 1.0 leads to a decrease of almost 70 % in the average erosion density of the hydrocyclone wall surfaces.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Hydrocyclones have been applied for many engineering processes for more than a century. Currently they are broadly used in industry for removal, classification or separation of particles in many mechanical and chemical processes such as reactors, dryers, removal of catalyst from liquids, wet flue gas desulfurization processes, treatment of waste water streams and advanced coal utilization such as fluidized bed combustion (Milin et al. 1992).
Desander hydrocyclones are used to provide reliable and efficient separation of sand and solid particles from water, condensate flows, and gas streams. They have proven to be a valuable part of many oil and gas production facilities in the petroleum industry. The desander cyclones are pressure-driven separators that require a pressure drop across the unit to cause separation of the solids from the bulk phase (water, oil, gas, etc.). It is typical to collect the solids in a closed underflow container or vessel, and periodically dump these solids. Desanded water/oil/gas in the central core section reverses direction and is forced out through the central vortex finder towards the overflow at the top of the cyclone (Process Group Pty Ltd. 2012).
Particles are exposed to a strong centrifugal force field sometimes up to 3000× gravitational acceleration (g). The flow enters the hydrocyclone with a linear motion; a high intensity force is then generated by movement of the slurry in a curving path through the cylindrical body. The hydraulic residence time in hydrocyclones is in a range of 1–2 s. This is an advantage when compared to the traditional gravity separators, which have residence times in the range of some couple of minutes. The solid particles are exposed to centrifugal acceleration and therefore, the settlement rate of particles will be varied in accordance to their various sizes, densities, and shapes. Due to an open overflow and high centrifugal forces, an air core may form in the hydrocyclone, which will increase the turbulent fluctuation and decrease separation efficiency. Although the cyclone geometries are quite simple, the flow behavior inside the cyclones is relatively complex. Occurrence of a strong air core in the center of the hydrocyclone causes the measurement of tangential and axial velocities to be a difficult task (Huang et al. 2009). However, with virtual experiments based on CFD techniques one should overcome these problems.
Pericleous and Rhodes (1986) are one of the first who predicted successfully the flow in a hydrocyclone. The improved Prandtl mixing length model was applied by them in order to simulate a separator with a diameter of 200 mm. They compared the velocity distribution with experimental results gained by laser Doppler velocimetry (LDV). Solutions to the equation of turbulent flow motion and a comparison of the solutions with LDV measured flow pattern of a 75-mm hydrocyclone was successfully performed by Hsieh and Rajamani (1991). A series of works on the simulation of hydrocyclones using the incompressible Navier–Stokes equations, complemented by an adequate turbulence model, have proven to be suitable for modeling the flow in hydrocyclones (Cullivan et al. 2004). The application of developed CFD techniques will alleviate some of the difficulties and problems when using models with empirical correlations (Vieira et al. 2011). Investigation of numerical methods for simulating a hydrocyclone was performed by Xu et al. (2009). They concluded that the re-normalization group (RNG) k–ε turbulence model was not appropriate for modeling flow in hydrocyclones. On the other hand, they found out that the Reynolds stress model (RSM) and the large eddy simulation (LES) model were able to provide better results in comparison with the experimental data. Ghadirian et al. (2013) modeled the air core using a transient two-phase simulation, with the results of the single phase runs as the initial input data. Afterwards, they performed final simulations involving particles and found out that the use of the LES turbulence model provides the best results matched to their experimental data. Monredon et al. (1992) developed mathematical models based on fluid mechanics involving some simplifying assumptions. Furthermore, Ipate and Căsăndroiu (2007) investigated the difference between the behavior of a series of various geometric configurations of hydrocyclones on the fluid dynamics. Chu and Chen (1993) applied the particle dynamics analyzer (PDA) to measure the size distribution of solid particles, concentration, and velocity profiles in a hydrocyclone. Wang et al. (2007) simulated the air core with the volume of fluid multiphase model (VOF) that tracks the interface between air and water. The VOF method is known for its ability to conserve the mass of the traced fluid, also when the fluid interface changes its topology. This change is traced easily, so the interfaces can for example join or break apart. The focus of the current paper is on erosion aspects of the hydrocyclone wall surfaces and therefore, only water was modeled as the primary phase and solid particles were modeled as the secondary phase. Erosion in hydrocyclones is an important phenomenon, which is not studied to our best knowledge in the literature in detail. Only Utikar et al. (2010) investigated the erosion caused by solid particles entrained in the gas flow in a cyclone separator. In the present study, beside the fluid dynamics study of a hydrocyclone and determination of separation efficiency curves using an Euler–Euler (Eu–Eu) approach, the particle tracking and erosion intensity inside the hydrocyclone are investigated in detail, applying the Euler–Lagrange (Eu–La) approach. The motivation for using Eu–Eu approach is that it can consider the particle–particle interactions by introducing granular quantity parameters such as temperature, pressure or viscosity, which can be derived from the kinetic theory. Nevertheless, prediction of modeling uncertainties is challenging and the computational costs for solving the additional transport equations are quite high, particularly if multiple particle classes are present in the flow. On the other hand, application of Lagrangian tracking involves the integration of particle paths through the discretized domain. Individual particles can be tracked from the injection area at the inlet until they escape from the domain. The Eu–La model has difficulties in considering the particle–particle interactions, especially if too many particles are present.
In the literature, there is a lack of experimental results for erosion of internal surfaces of a hydrocyclone. Therefore, in the current study, the experimental results concerning flow behavior and separation efficiency are used initially to validate the Eu–Eu simulation results. This has validated the application of a proper turbulence model and correct input conditions for further simulations with the Eu–La technique.
2 Hydrocyclone geometry
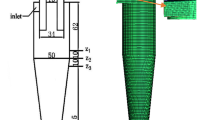
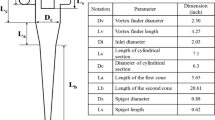
A typical hydrocyclone as depicted in Fig. 1 consists of a cylindrical body, a conical body, open discharge at the bottom called the underflow outlet, a tangential inlet to the cylindrical part of the cyclone body, and an overflow discharge part. The cylindrical body is closed on its top with a plate through which passes an axially located overflow pipe, which is called the vortex finder (Vieira et al. 2010). In Fig. 1, A–A, B–B, and C–C are axial positions at 60, 120, and 180 mm distances from the top of the hydrocyclone, respectively. The experimental database of hydrocyclone flow of Hsieh (1988) (geometrical data see Table 1), providing velocity profiles within the hydrocyclone measured by the LDV method and also results concerning the particle classification were used to validate our CFD simulation results. Hsieh (1988) used a pumped recirculation system to measure the particle classification efficiency of hydrocyclones using a microtrac particle analyzer (Milin et al. 1992). The Euler number of the cyclone is the well-known pressure loss factor defined by the following equation:
where ∆p is the pressure drop across the cyclone; v i is the superficial velocity in the cyclone body as the characteristic velocity; and ρ is the density of the liquid phase. Based on the various input conditions and the resulting pressure loss, the Euler number for the hydrocyclone is simply calculated using Eq. (1). Moreover, the separation efficiency of the hydrocyclone for various input solid concentrations is presented later in this work.
The hydrocyclone geometry and subsequently the mesh were generated with ANSYS-ICEM (14.5). The structured mesh (hexahedral elements) was created using the O-grid technique as depicted in Fig. 2 with a considerably high quality. Grid study was performed to find an optimal mesh size and quality in order to have mesh-independent CFD results. The grid study was first performed by simulating the hydrocyclone in ANSYS-CFX without coupling the erosion model. It was observed that taking the outlet velocity components at overflow and underflow as the grid study criterions, a fine mesh with around 150,000 elements would be sufficient to obtain mesh independent results with a low deviation of about 0.3 %, which is presented in detail in Table 2. The deviation values in percentage as presented in Tables 2 and 3 were calculated using the following equation:
where d n is the deviation; Z n and Z n−1 define the value of a simulation output with the mesh steps n and n − 1, respectively. Additionally, a grid study was performed with coupling an erosion model with CFD simulations. The average erosion rate on hydrocyclone walls was considered here as the grid study parameter. It was observed that a fine mesh with around 700,000 elements, specifically with mesh refinement next to the wall surfaces, would be sufficient to obtain mesh independent results with a low deviation of 0.56 %, which is presented in detail in Table 3. Therefore, the model with 150,000 mesh elements was used in Eu–Eu simulations for only the flow behavior studies and the model with 700,000 mesh elements was used in Eu–La simulations for the particle tracking and erosion studies.
3 CFD simulations
3.1 Euler–Euler approach
In the present study, an Eu–Eu approach was applied to model the highly laden liquid–solid mixture in the hydrocyclone, to predict the particle–particle interactions, the flow behavior in the hydrocyclone, and the separation efficiency. Here, the focus was on the full Eulerian approach employing momentum transport equations for each phase since it is more accurate. However, the computational effort is increased compared to the mixture model. A separate set of mass, momentum, and energy conservation equations is solved for each phase. The continuity equations for the both phases considering isothermal condition are given as Eqs. (3) and (4) for the liquid (fluid) phase and the particle phase, respectively.
The incompressible momentum equations for the liquid and particle phases are derived as follows:
where ρ f and ρ p are the density of the fluid and the particle, respectively; u f and u p are the velocity of the fluid and the particle, respectively; ε f and ε p are the volume fraction of the fluid and particle, respectively; M is the particle–fluid interaction source term; ∇P is the pressure gradient term; ∇P p is the particle–particle interaction term; and τ indicates the viscous shear stress tensor. Forces that impacted the particles were namely the drag force which was modeled by the Gidaspow drag model, the lift force which was modeled by the Saffman–Mei lift model, the pressure force, and the added mass force. For modeling the turbulence, the turbulence models of k–ε, k–ω, Menter’s shear stress transport (SST), and baseline Reynolds stress model (BSL-RSM) were applied for the liquid (continuous) phase. For the solid phase, the zero equation model was applied, which computes the turbulence fluctuations via the data from the fluid phase.
3.2 Euler–Lagrange approach
In this approach water is treated as the continuum phase and the abrasive particles are traced in a Lagrangian reference frame. This approach is known as a discrete particle or Eu–La model. Since each particle is tracked from its injection location to the final destination point, the tracking procedure is applicable to the steady state flow analysis. In the second part of the current study, the Eu–La approach was applied to track the abrasive solid particles and to predict the location and intensity of erosion on hydrocyclone wall surfaces. For erosion computations, the particles should be traced inside the domain by considering the particles as the discrete phase. Moreover, the application of the Eu–La approach is essential when multiple particle classes are present. A simplified set of incompressible Navier–Stokes equations is solved in this approach for the liquid phase consisting of mass conservation:
and the momentum conservation:
The momentum source due to the drag force of particles, F D,s, is monitored and accumulated in every cell as the particles are passing. The particle trajectories are predicted based on the liquid phase velocity field by evaluation of a local momentum balance as follows:
In Eq. (9), the particle acceleration is due to the drag force and the gravitational acceleration. The drag coefficient, C D, can be derived from the following equation:
where the coefficients a 1–3 are given for various ranges of particle Reynolds number (Rep) from 0.1 to 50,000 by Morsi and Alexander (1972). Twelve transport equations have to be solved when using the Eu–La model. An additional particle class can be added without the need of a further transport equation. Therefore, for consideration of different particle classes, the Eu–La approach is much cheaper than the Eu–Eu approach.
4 Boundary conditions
In the CFD simulations, the Reynolds averaged Navier–Stokes equations (RANS) for both Eu–Eu and Eu–La methods were supplemented by applying the k–ε, k–ω, SST, and BSL-RSM turbulence models for comparison. The numerical solution of the equations was based on the finite volume method (FVM). The correct selection of turbulence models is an important and challenging task in predicting the turbulent features of the flow inside the hydrocyclone.
4.1 Inlet boundary conditions
At the inlet boundary of the hydrocyclone, the fluid inlet velocity was set according to the experimental data of Hsieh (1988). The injection position of solid particles was the inlet surface. The velocity of particles was assumed to be equal to the fluid inlet velocity (Wan et al. 2008). A number of 100,000 particles were fed into the hydrocyclone. The particles used were fine fire-dried sand, whose density was 2300 kg/m3, needed as the value for the modeling. The pressure level was set in the hydrocyclone feed according to experimental operating conditions. In Eu–Eu simulations for separation efficiency computations, diameters of the particles were given as single-input values in the range of 3–180 μm and the sand loading C s was varied from 14.4 wt% to 55.8 wt% according to the experimental conditions of Hsieh (1988).
On the other hand, for erosion modeling, the diameters of sand particles used in our hydroabrasion studies have been measured experimentally with a HORIBA particle size analyzer (Retsch Technology, LA950 model). In Eu–La simulations for the erosion studies, instead of a single particle size, a particle size distribution as depicted in Fig. 3 was given as an input. The four main characteristic parameters for defining a particle size distribution curve are the minimum diameter, maximum diameter, mean diameter, and the standard deviation value. Based on the distribution of measured size in Fig. 3, the minimum diameter was set to 67.5 µm, the maximum diameter to 678.5 µm, the mean diameter to 263.9, and finally the standard deviation value was set to 105.4 µm. The sand concentration was applied from 5 wt% to 15 wt%.
4.2 Outlet boundary conditions
At the hydrocyclone underflow and overflow parts, the pressure outlet boundary condition was set at a given standard atmospheric pressure condition.
4.3 Wall boundary conditions
On hydrocyclone walls, a no-slip condition was assumed. The grid nodes in the vicinity of walls were approximated and treated using the wall function. The wall roughness was given as 1.5 µm in the simulations for the stainless steel 410 as the wall material.
4.4 Coefficient of restitution
The coefficient of restitution was also applied on the wall surfaces of the hydrocyclone. The restitution coefficient for an orthogonal contact of a particle against a rigid surface is defined as the ratio of the rebound velocity to the impingement velocity. For a non-orthogonal contact as shown in Fig. 4, the behavior of the center of the particle after the rebound can be defined through the normal (R n) and tangential restitution coefficients (R t) with Eqs. (11) and (12), respectively.
where V ni and V nr are the normal velocity components of the particle before and after the impact with the surface, respectively. V ti and V tr are the tangential velocity components of the particle before and after the impact with the surface, respectively. The restitution coefficient depends on a considerable number of parameters, mainly on particle material properties, particle size, particle shape, impact velocity, impact angle, and target surface material properties. The particles rebound dynamics can only be described statistically since the particles in practical applications are irregular in shape and vary in size. When the hardness of particles is higher than the target material, their continuous impact causes the surface to become pitted with craters after some incubation period. When the impact duration becomes longer, it causes ripple patterns to be created on the eroded surface. Consequently, the local impact angle may vary for each particle as it impacts the eroded surface (Tabakoff et al. 1996).
Wan et al. (2008) defined the coefficient of restitution for the cyclone walls using a trial and error method. They adopted different coefficients of restitution at different wall positions. When the calculated separation efficiency of cyclone showed a good agreement with the experimental result using a certain coefficient of restitution, it was adopted. By assuming that the particle size and shape remain unchanged through the passage from the inlet to the spigot, the impact velocity and impact angle of particles with respect to the cyclone wall are changing from top to bottom of the hydrocyclone. For the current study, according to Wan et al. (2008), the particle coefficient of restitution was set as 1.0–0.9 at the annular space. From top to bottom of the separation space (cylindrical body part), the particle coefficient of restitution was set as 0.9–0.6, and at the dust hopper (conical part), the particle coefficient of restitution was set as 0.5–0.05 as a linear function of height.
4.5 Solver control
A small physical time scale is required when having large regions of separated flow or multiphase flow. The option of a local timescale factor allows different time scales to be applied in different regions of the simulation domain. Smaller time scales are used in regions of the flow where the local time scale is quite short such as for fast flows. The bigger time scales are applied for regions where the time scales are locally large, similar to the slow flows. Local timescale factor is a different approach for controlling how fast the equations in the non-linear loop will be solved. The simulations were run in a steady state mode. Convergence was defined by RMS residuals less than 10−5 and imbalances (conservation) less than 10−2 for all variables. Under these simulation conditions, the residues were enough to guarantee the convergence.
5 Flow behavior and separation efficiency
Efficiency of separation, η, is a common measure of the efficiency of screening or cleaning of the cyclone. A theoretical relation exists between the fluid variable and physical characteristics of the system. The classification performance of a hydrocyclone is influenced by the design variables such as the hydrocyclone dimension and the operating variables such as the feed pressure and physical properties of solid particles and also the resulting mixture flow at the inlet. The separation efficiency curve expresses the relationship between the weight fraction or percentage of each particle size of the feed flow and the underflow discharge. The separation efficiency η is formulated as
where w p,inlet is the percent by weight of particles at the inlet; and w p,overflow is the weight percentage of particles at overflow.
The particle size is commonly used to represent the performance of the hydrocyclone. The tangential motion of the liquid flow generates centrifugal forces; since the particles have a different density from the liquid density, a radial velocity with reference to the liquid will be generated on the particles (Rietema 1961). The direction of the radial velocity is outwards and when the centrifugal forces are relatively strong, the particle can reach the cyclone walls through its motion towards the downward discharge and is then separated. A particle may not reach the wall under the three following conditions:
(a) If the radial velocity of the liquid which is directed inwards is large and thus causes it to be entrained towards the center of the hydrocyclone.
(b) If it enters into the hydrocyclone at a great distance from the walls.
(c) If the particle residence time is too short in comparison with the average residence time in hydrocyclones (Dwari et al. 2004).
The addition of solid particles increases the viscosity of the slurry flow significantly compared to the viscosity of the pure fluid. For diluted mixtures, the fluid can still be considered as a Newtonian fluid; however, the effect of solid particles in the flow through the modification of the viscosity must be considered while applying single-phase simulations (Romero et al. 2004). The slurry viscosity can be described as relative to the viscosity of the liquid phase. Depending on the size and concentration of the solid particles, several models exist that describe the relative viscosity as a function of volume fraction C v of solid particles. In this study, Eq. (14) expressed by Thomas (1965) was applied to calculating the viscosity term of the slurry flow. Afterwards, this was used to find out an assumed value for the viscosity term for solid particles as an input parameter for material definition in Eu–Eu simulations.
where μ f is the fluid viscosity; μ m is the viscosity of the mixture; and C v is the volume fraction of the solid particle given as
where C p is the concentration of the solid particles in weight fraction; ρ m, ρ p, and ρ f are the densities of the mixture, the solid particle phase, and the fluid phase, respectively. The density of the mixture ρ m can be described by the following equation:
By defining the mixture viscosity μ m with Eq. (14), the assumed viscosity of the sand particles, μ p, was finally calculated from Eq. (17), and used for definition of physical properties of the sand particles in the liquid flow.
The water flow streamlines inside the hydrocyclone obtained by the Eu–Eu method are shown in Fig. 5. Under the combined effects of centripetal buoyancy and fluid drag force, a high amount of water, which is the light phase, will discharge as depicted in Fig. 5 from the overflow outlet and the suspension is withdrawn at the underflow with a relatively high solid concentration. In Fig. 6, three single sand particles with different diameter sizes of 20, 100, and 600 µm were tracked inside the hydrocyclone from the inlet feed to the outlets by consideration of the fully coupled interactions of the two phases. The selection of these three diameters was chosen in order to show the difference among the streamlines of various particle sizes inside the hydrocyclone. It was observed that due to the centrifugal force field, the 20-μm particles were carried out through the overflow but the bigger particles discharged through the spigot at the underflow outlet.
The k–ε turbulence model, SST model, two equation k–ω model, and the BSL Reynolds stress model were used to simulate the flow inside the hydrocyclone. The modeling results were used to calculate the separation efficiency curves for comparison with experimental results of Hsieh (1988). For the k–ε, SST, and k–ω turbulence models, two transport equations were used; however for the BSL-RSM, five additional transport equations had to be applied. The ANSYS-CFX tool was used to solve the governing set of partial differential equations for the mixture flow and turbulent components. The CFD results using the k–ε model deviate a lot from the experimental results and therefore, they are not presented here. The cut size d 50 is the particle size at which the efficiency of hydrocyclone is 50 %. The cut size is predicted from the CFD simulations and is approximately 33 μm as depicted in Fig. 7, when the solid concentration is 14.4 wt% and the total input mass flow is 1.19 kg/s. Each simulation point in Figs. 7, 8, and 9 represents a simulation run with a specified constant mean diameter for the particle stream ranging from 3 µm to 180 µm. The cut size, d 50, increases with an increase in the solid concentration. For example, the cut size with a solid concentration of 55.8 wt% is approximately 106 μm (see Fig. 9). The total mass flow is 1.41 and 1.97 kg/s, respectively, when the solid concentrations are 35 % and 55.8 %.
Satisfactory results are obtained by applying the k–ω and SST turbulence models but only for relatively low solid particle loadings in the feed flow. Results obtained with three different turbulence models of SST, k–ω, and BSL Reynolds stress model are shown in Fig. 7. All the CFD results are in fair agreement with experimental results. However, the simulation results obtained with the BSL RSM fit very well to the experimental data in Fig. 7, especially for particles larger than the cut size. Deviation may be due to the absence of a curvature term. This term is important for the strong swirling flows inside the hydrocyclone (Stephens and Mohanarangam 2009). These deviations increase with an increase in the solid concentration in the feed flow, especially for larger particle sizes (bigger than 100 μm) as presented in Figs. 8 and 9. As it was mentioned, the presence of solid particles increases the viscosity of the slurry flow significantly compared to the viscosity of the pure fluid. Therefore, for high solid concentrations, as it is the case for the simulation with 35 wt% and 55.8 wt% sand concentration, the consideration of the suspension as a Newtonian fluid is not any longer a valid assumption. Moreover, as the solid concentration increases, the importance of modified and precise modeling of particle–particle interactions will arise. The results of all the turbulence models at higher solid loading, especially when the particle size is relatively large, are not in very good agreement with the experimental data. Overall, it was observed that the CFD results obtained by the BSL-RSM, which is a seven differential equation turbulence model, are in better agreement with experimental data compared with the CFD results obtained by the two equation turbulence models of SST and k–ω. However, the computational time for the BSL-RSM is relatively higher than the other two turbulence models. The improvement obtained by the BSL-Reynolds stress model is still far lower than the error between the experimental data and simulation results for high solid loadings as shown in Figs. 8 and 9. It should be noted that at higher concentrations, interaction among the particles increases drastically. Therefore, it is essential to perform four-way coupled simulations instead of two-way coupled simulations in order to capture the precise flow behavior of particulate flows with a high solid loading. Four-way coupled simulation takes the particle–particle interactions also into account in comparison with two-way coupled simulation, which takes only the fluid on particles and particles on fluid effects. On the other hand, for higher concentrations, the viscosity of the slurry flow increases significantly compared to the viscosity of the pure fluid. Therefore, the consideration of the suspension as a Newtonian fluid leads to large deviations for higher concentrations as shown in Fig. 9.
In Fig. 10a, the velocity vectors of sand particles are shown at various heights from the top of the hydrocyclone. When a particle initially flowed down due to the external downward flow, at the same time the radial velocity directing to the center of hydrocyclone forces the particle to be moved inward (Wang et al. 2007). When the particle is small, the resulting inward drag force is higher than the centrifugal force, which causes the particle to be caught by the upward inner flow and discharged through the vortex finder. The bigger or heavier particles flow towards the downward discharge, as the centrifugal force acting on the particle is higher than the inward drag force.
The timescale factor is an essential parameter for steady state simulation of flow inside the cyclones. Applying a timescale factor of for example 1.0 as shown in Fig. 10b would not be sufficient to simulate the central core in a steady way as simulated by a smaller timescale factor of 0.4 depicted in Fig. 10c. The relatively low fluctuation of the central core in Fig. 10c matches with the findings in the literature such as that by Cullivan et al. (2004). Figures 11, 12, 13 show comparisons of the simulated tangential and axial velocity profiles at three different axial positions of 60, 120, and 180 mm from the top of the hydrocyclone, defined as the A–A, B–B, and C–C planes in Fig. 1, respectively. As shown in Figs. 11, 12, 13, the results obtained by CFD simulations are in good agreement with experimental results of Hsieh (1988).
According to Panton (2013), the tangential velocity profile could be defined as a Rankine vortex having a quasi-forced vortex in the inner part and a quasi-free vortex in the outer section. It is possible to say that the tangential velocity profile has a trend like an inverse W and the axial velocity profile has a trend like an inverse V at the distinct axial locations inside the hydrocyclone. The axial velocity distributions at all locations of 60, 120, and 180 derived from the CFD runs are shown in Fig. 14. As it is depicted, the axial velocities of particles decrease as the distance from the top increases. The velocity magnitudes even reach negative values near the walls or in the outer part of the flow, while the slurry flow travels towards the bottom of the hydrocyclone.
6 Erosion modeling
Impact erosion is characterized by individual particles contacting the surface at a certain angle and velocity. Removal of material over time occurs through small-scale deformation, cutting, fatigue cracking or a combination of these, depending on the properties of the erodent material and the target surface. The required information on particle dynamics and rebound characteristics has been developed such that the particle trajectories inside the hydrocyclone can be predicted. The material removal process can then be calculated using this trajectory and impact data. The equations developed for predicting the erosion rates are homogeneous in nature, this means they can be applied to calculate the material loss resulting from a given particle entering the system at a given location and rebounding in a given manner (Grant and Tabakoff 1975).
Grant and Tabakoff (1973) have experimentally proved that the wear of a material is mostly dependent on the impingement angle and the impact velocity of abrasive particles. The uniqueness of this model compared to other erosion models of its kind is that it contains the particle impact restitution coefficient as an influencing parameter and in particular the tangential restitution coefficient R t as the decisive parameter affecting the erosion rate. Equation (18) was developed by Grant and Tabakoff (1973) to predict the erosion of ductile metals and alloys and is defined as the ratio of the eroded mass of target material to the mass of impinging solid particles. They assumed that the erosion process is dependent on two mechanisms; one at low angles of impingement; one at high angles of impingement; and a combination of the two at intermediate impact angles. The relationship for erosion was derived as Eq. (18). The first term of this expression predominates at low angles of attack, whereas the second term predominates at normal impact where the tangential velocity approaches zero.
where k 1 is the material constant; f(β i) is the empirical function of particle impact angle; V ti and V tr are the tangential components of incoming particle velocity and of rebounding particle velocity, respectively; f(V ni) is the component of erosion due to the normal component of velocity. By inserting V ti = V i cos β i, the erosion equation can be written as
The particle impact angle influences the erosion rate in a very special way, as it was found that the maximum erosion rate occurs at an impact angle of 30°, whereas only a residual amount of erosion results from the normal impact. The effect of the particle impact angle is lumped into f(β i), and a strict empirical approach is used to predict its behavior (Grant and Tabakoff 1973). The result of this analysis yields the following expression:
where β 0 is the angle of attack where the maximum erosion occurs; k 12 is a material constant and
The component of erosion resulting from normally impacting particles is expressed as
The investigated hydrocyclone in this study was constructed from stainless steel 410 faced to the two-phase water–sand flow. Stainless steel 410 is a basic martensitic grade, which contains 11.5 % chromium, offering both exceptional wear and corrosion resistance. The constants and the angle of maximum erosion required for the Grant–Tabakoff erosion model for the stainless steel 410, eroded by sand particles (SiO2) are given in Table 4 based on the experimental work of Clevenger and Tabakoff (Clevenger and Tabakoff 1975). Total erosion rate of the wall due to the solid particles interactions with the wall is finally computed from the following equation:
where \( \dot{N} \) is the number rate of solid particles; and m p is the particle mean mass.
As it has already been mentioned, the Eu–La approach was applied to predicting the erosion rate or the material loss of the hydrocyclone wall surfaces. The erosion leads to physical damage and functional failure, since even small deformations on the hydrocyclone wall can interrupt the pressure profile and cause a decrease in the separation efficiency. As depicted in Fig. 15, the particles followed a distinct path rather than a tangled movement on hydrocyclone walls while flowing down. According to the particle tracking inside the hydrocyclone, the erosion location and its density rate on the wall surfaces were predicted with the Grant-Tabakoff erosion model and presented in Fig. 16 as an illustrating example. The input conditions for the results in Figs. 15 and 16 were the solid concentration of 15 wt%, input flow velocity of 2.7 m/s, particle size distribution as given in Fig. 3, assumption of spherical sand particles, and the isothermal assumption of the flow in the hydrocyclone. The most eroded part was at the intersection between the cyclone cylindrical part and the conical part, which was in good agreement with the findings of Utikar et al. (2010). At the region close to the underflow discharge, the erosion is quite low although due to the area restriction and rise of the solid concentration, a different outcome could be expected. The reason is that in this region, almost all the particles are sliding on the walls and therefore the impact angle is close to 0°. The resulting erosion is therefore less than the erosion in central parts where the particles impact the walls with various angles, causing the chipping and cutting mechanisms to occur. The particle size distribution used in the simulations is that of the standard sand being used in our hydroabrasion experiments presented in Fig. 3.
6.1 Particle concentration effect
The particle concentration is very often interpreted as the percentage content by weight or by volume of the particles in a gaseous or liquid medium. With an increase in the particle concentration, more particles strike the target surface and therefore enhance the erosion. In Fig. 17, the effect of solid particle concentration on the average and maximum erosion rate in the hydrocyclone is depicted. As expected, the erosion rate or the material loss of hydrocyclone walls increases with an increase in the sand concentration in the range of 15–55 wt%. The total mass flow rate for 15 wt% solid concentration was 1.19 kg/s. The constant input conditions here were the input flow velocity of 2.7 m/s, the particle size distribution as given in Fig. 3, the assumption of spherical sand particles, and the isothermal assumption of the flow in the hydrocyclone. The erosion rate as a function of the solid concentration is expressed by a linear curve in the logarithmic scale of y axis. When the sand concentration is quite small, the interaction among particles can be ignored and the erosion increases linearly with the sand loading. However, when the sand concentration is large enough, the interaction among particles has to be taken into account. It should be mentioned that the erosion rates shown in Figs. 17, 18, 19, 20, 21 and 22 give a global measure of the erosion within the whole internal surfaces of the hydrocyclone.
In Fig. 18, the erosion rate and locations of material losses on hydrocyclone walls for two sand particle concentrations of 5 wt% and 15 wt% are shown and compared with each other. The constant input conditions here were the input flow velocity of 2.7 m/s, the particle size distribution as given in Fig. 3, the assumption of spherical sand particles, and the assumption of isothermal flow in the hydrocyclone. As depicted, an erosion field at the upper part of the cylindrical body of the hydrocyclone appeared and developed, when the solid concentration was increased. The erosion density at the intersection of cylindrical to conical body was also relatively increased.
6.2 Flow velocity effect
In Fig. 19, the effect of the inlet feed velocity on the erosion is presented. The constant input conditions here were the sand concentration of 15 wt%, the particle size distribution as given in Fig. 3, the assumption of spherical sand particles, and the assumption of isothermal flow in the hydrocyclone. The trend of erosion shows an increase as a potential function in a logarithmic scale as the feed velocity increases. The erosion rate increases with the impact velocity to a power m, varying between 1.5 and 3.5 in experiments carried out in different laboratories. The exponent m averages around 2 for wear on metal plates by a water-sand jet, between 1 and 4 in slurry pipes, and from 2.2 to 3 in centrifugal pumps. The dispersion of values for m can be explained by the diversity of mechanisms and the mean flow parameters, as well as differences in experimental methods (Shook and Roco 1991). However, this effect will be up to a certain velocity and afterwards the erosion rate would increase only slightly. The power coefficient m changes with particle breakage, which depends on the erodent material. Brittle particles break intensely upon impact with the target material, which causes a sharp decline in the value of exponent m.
6.3 Particle size effect
An increase in the particle size at a constant solid concentration decreases the number of particles suspended in the mixture and at the same time increases the kinetic energy per particle impact. Thus the increase in wear with an increase in particle size is generally attributed to the increase in energy available for erosion (Desale et al. 2009). Grant and Tabakoff (1975) found that the increase in the particle size did not influence the erosion after a certain threshold value was reached.
The effect of the sand particle size is shown in Fig. 20. The constant input conditions here were the sand concentration of 15 wt%, the input flow velocity of 2.7 m/s, the assumption of spherical sand particles, and the assumption of isothermal flow in the hydrocyclone. The increasing trend of erosion or material loss in this case can be described by a polynomial function in a logarithmic scale, when the particle size increases in the range of 100–700 μm. As the particle size increases, there are fewer particles to impact the surface and this results in lower impact rate. However, each particle will be heavier and thus will have greater kinetic energy. Therefore, it is difficult to quantify the sand size effect as the competing effects between kinetic energy of the particle and impact rates must to be taken into account (Rajahram et al. 2011).
In Fig. 21, the erosion rate and location of material loss of hydrocyclone walls for two various particle sizes of 20 µm and 100 µm are shown and compared with each other. As it is expected, the erosion rate caused by solid particles with smaller size is lower than the erosion caused by bigger particles. For the 20 µm particles, there is no signs of erosion at the lower body parts of the hydrocyclone while most of the particles are discharged from the upper outlet. However, the erosion at the vortex finder through the upper discharge appears and is developed in the way which the particles travel towards the upper outlet (overflow). As the larger particles roll down the conical part, the centrifugal force on the particle increases. The radius of the hydrocyclone conical part decreases as the flow passes towards underflow. However, the tangential velocity of the particle remains almost the same.
6.4 Particle shape effect
The effect of the particle shape factor on erosion was also investigated and the simulated results are given in Fig. 22. The constant input conditions here were sand concentration of 15 wt%, input flow velocity of 2 m/s, the particle size distribution as given in Fig. 3, and the assumption of isothermal flow in the hydrocyclone. The shape factor is determined using the following equation:
where A is the projected area of the particle; and p e is the perimeter of the particle (Desale et al. 2008). The shape factor of 0 is assumed for a disk-shaped particle and 1.0 for an ideal spherical shape. A cross-sectional area factor was included to modify the assumed spherical cross section area to allow for non-spherical particles. This factor was multiplied by the cross section area calculated assuming spherical particles. This affects the drag force calculated by ANSYS-CFX. Results indicate that the more the particles are sharped edged, the more they are erosive and result in an increase in erosion of the hydrocyclone walls. It is observed that an increase in the particle shape factor from 0.1 to 1.0 leads to a decrease in almost 70 % in the average erosion density of the hydrocyclone walls.
7 Conclusions
Hydrocyclones are designed to achieve a reasonably good separation between solid particles of various sizes or between solid particles and liquid flow. CFD simulations using ANSYS-CFX (14.5) were performed to investigate the slurry flow behavior and erosion rates inside a hydrocyclone. The consideration of an appropriate erosion model and specifically the erosion rate parameter is an important factor in the grid study. The number of elements of the final mesh to obtain mesh independent results was not identical with and without application of the erosion model in the CFD simulations. The grid study was initially carried out by simulating the hydrocyclone in ANSYS-CFX without coupling the erosion model. It was observed that taking the outlet velocity components at overflow and underflow as the grid study criterions, a fine mesh with around 150,000 elements would be sufficient to get mesh independent results. Afterwards, a grid study was carried out by coupling an erosion model with CFD simulations. The average erosion rate on hydrocyclone walls was considered here as the grid study parameter. It was observed that a fine mesh with around 700,000 elements, with specifically mesh refinement next to the wall surfaces, would be sufficient to get mesh independent results. In simulations for predicting the erosion, a much finer mesh at the vicinity of the wall surfaces is required in order to precisely model the particle–particle and particle–wall interactions near the surface.
The Euler–Euler approach was used to study the flow behavior and prediction of separation efficiency curves of the hydrocyclone. The Euler–Euler approach was capable of considering the particle–particle interactions and was appropriate for highly laden liquid–solid mixtures. The effect of solid mass loading on the separation efficiency of the hydrocyclone was also studied. The cut size d 50 was predicted from the CFD simulations and was approximately 33 μm when the solid concentration was 14.4 wt% and the total input mass flow 1.19 kg/s. The cut size increased with an increase in the solid concentration. For example, the cut size with a solid concentration of 55.8 wt% was approximately 106 μm. Among the investigated turbulence models in the current study, the results obtained from the BSL-RSM matched better with the experimental results. However, the computational costs and simulation time were relatively higher in comparison with SST and k–ω turbulence models. The results of particle velocity profiles in distinct axial positions inside the hydrocyclone predicted by CFD simulations were validated with experimental results of Hsieh (1988) and showed a good agreement.
The Euler–Lagrange approach was applied to predicting the location and quantity of erosion on the hydrocyclone wall surfaces. The abrasive particles were traced in a Lagrangian reference frame as discrete particles. The most eroded part was at the intersection between the hydrocyclone cylindrical and conical body parts, which was in good accordance with the findings of Utikar et al. (2010). From a spatial analysis of the erosion rates, one can conclude that increases in the feed velocity, solid concentration, and particle size increased the erosion field at the upper part of the cylindrical body in front of the tangential inlet. The erosion density in the cylindrical to conical part transitional field in comparison to the other regions was also increased. Moreover, it was observed that an increase in the particle shape factor from 0.1 to 1.0 led to a decrease of almost 70 % in the average erosion density of hydrocyclone walls. Modeling of the change in geometry associated with erosion and the effects of erosion profiles on the fluid flow was postponed for subsequent works. Modeling the 3-D deformation of hydrocyclone walls due to erosion requires a finite element modeling (FEM) technique coupled to the CFD simulations. Such FEM-CFD coupling required long and costly transient simulations. Detailed hydroabrasion experiments in a broader range are planned to be undertaken.
References
Chu L, Chen W. Research on the motion of solid particles in a hydrocyclone. Sep Sci Technol. 1993;28(10):1875–86. doi:10.1080/01496399308029247.
Clevenger WB, Tabakoff W. Erosion in radial inflow turbines—vol. IV: erosion rates on internal surfaces. Technical Report. University of Cincinnati; 1975.
Cullivan JC, Williams RA, Dyakowski T, Cross CR. New understanding of a hydrocyclone flow field and separation mechanism from computational fluid dynamics. Miner Eng. 2004;17(5):651–60. doi:10.1016/j.mineng.2004.04.009.
Desale G, Gandhi B, Jain S. Slurry erosion of ductile materials under normal impact condition. Wear. 2008;264(3–4):322–30. doi:10.1016/j.wear.2007.03.022.
Desale G, Gandhi B, Jain S. Particle size effects on the slurry erosion of aluminium alloy (AA 6063). Wear. 2009;266(11–12):1066–71. doi:10.1016/j.wear.2009.01.002.
Dwari R, Biswas M, Meikap B. Performance characteristics for particles of sand FCC and fly ash in a novel hydrocyclone. Chem Eng Sci. 2004;59(3):671–84. doi:10.1016/j.ces.2003.11.015.
Ghadirian M, Hayes RE, Mmbaga J, Afacan A, Xu Z. On the simulation of hydrocyclones using CFD. Can J Chem Eng. 2013;91(5):950–8. doi:10.1002/cjce.21705.
Grant G, Tabakoff W. An experimental investigation of the erosive characteristics of 2024 Aluminum alloy. Technical Report. Cincinnati University; 1973.
Grant G, Tabakoff W. Erosion prediction in turbomachinery resulting from environmental solid particles. J Aircr. 1975;12(5):471–8.
Hsieh K. A phenomenological model of hydrocyclone. Ph.D. Thesis. University of Utah; 1988.
Hsieh K, Rajamani R. Mathematical model of the hydrocyclone based on physics of fluid flow. AIChE J. 1991;37(5):735–46. doi:10.1002/aic.690370511.
Huang J, An L-S, Wu Z-Q. Study of application and operation optimization of hydrocyclone for solid–liquid separation in power plant. In: Proceedings of the world congress on engineering and computer science 2009, vol. I, 20–22 Oct 2009, San Francisco; 2009.
Ipate G, Căsăndroiu T. Numerical study of liquid–solid separation process inside the hydrocyclones with double cone sections. UPB Sci Bull. 2007;69(4):83–94.
Milin L, Hsieh K, Rajamani R. The leakage mechanisms in the hydrocyclone. Miner Eng. 1992;5(7):779–94. doi:10.1016/0892-6875(92)90246-6.
Monredon TC, Hsieh K, Rajamani R. Fluid flow model of the hydrocyclone: an investigation of device dimensions. Int J Miner Process. 1992;35(1–2):65–83. doi:10.1016/0301-7516(92)90005-H.
Morsi SA, Alexander AJ. An investigation of particle trajectories in two-phase flow systems. J Fluid Mech. 1972;55(2):193–208. doi:10.1017/S0022112072001806.
Panton RL. Incompressible flow. 4th ed. New Jersey: Wiley; 2013.
Pericleous K, Rhodes N. The hydrocyclone classifier—a numerical approach. Int J Miner Process. 1986;17(1–2):23–43. doi:10.1016/0301-7516(86)90044-X.
Process Group Pty Ltd. Hydrocyclones desander. Process Group Pty Ltd: Rowville; 2012.
Rajahram SS, Harvey TJ, Wood R. Electrochemical investigation of erosion–corrosion using a slurry pot erosion tester. Tribol Int. 2011;44(3):232–40.
Rietema K. Performance and design of hydrocyclones-III: separating power of the hydrocyclone. Chem Eng Sci. 1961;15(3–4):310–9. doi:10.1016/0009-2509(61)85035-5.
Romero J, Sampaio R, da Gama RS. Numerical simulation of flow in a hydrocyclone. Lat Am Appl Res. 2004;34:1–9.
Shook CA, Roco MC. Slurry flow: principles and practice. Stoneham: Butterworth-Heinemann; 1991.
Stephens DW, Mohanarangam K. Turbulence model analysis of flow inside a hydrocyclone. In: Seventh international conference on CFD in the minerals and process industries CSIRO, Melbourne; 2009.
Tabakoff W, Hamed A, Murugan DM. Effect of target materials on the particle restitution characteristics for turbomachinery application. J Propul Power. 1996;12(2):260–6. doi:10.2514/3.24022.
Thomas DG. Transport characteristics of suspension: VIII. A note on the viscosity of Newtonian suspensions of uniform spherical particles. J Colloid Sci. 1965;20(3):267–77. doi:10.1016/0095-8522(65)90016-4.
Utikar R, Darmawan N, Tade MO, et al. Hydrodynamic simulation of cyclone separators, Chap. 11. Croatia: InTech; 2010.
Vieira LG, Damasceno JJ, Barrozo MA. Improvement of hydrocyclone separation performance by incorporating a conical filtering wall. Chem Eng Process. 2010;49(5):460–7. doi:10.1016/j.cep.2010.03.011.
Vieira LG, Silverio BC, Damasceno JJ, Barrozo MA. Performance of hydrocyclones with different geometries. Can J Chem Eng. 2011;89(4):655–62. doi:10.1002/cjce.20461.
Wan G, Sun G, Xue X, Shi M. Solids concentration simulation of different size particles in a cyclone separator. Powder Technol. 2008;183(1):94–104. doi:10.1016/j.powtec.2007.11.019.
Wang B, Chu KW, Yu AB. Numerical study of particle–fluid flow in a hydrocyclone. Ind Eng Chem Res. 2007;46(13):4695–705. doi:10.1021/ie061625u.
Xu P, Wu Z, Mujumdar A, Yu B. Innovative hydrocyclone inlet designs to reduce erosion-induced wear in mineral dewatering processes. Dry Technol. 2009;27(2):201–11. doi:10.1080/07373930802603433.
Acknowledgments
The authors would like to thank “Stiftung Rheinland-Pfalz für Innovation, Mainz, Germany,” for financial support.
Author information
Authors and Affiliations
Corresponding author
Additional information
Edited by Yan-Hua Sun
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Azimian, M., Bart, HJ. Numerical analysis of hydroabrasion in a hydrocyclone. Pet. Sci. 13, 304–319 (2016). https://doi.org/10.1007/s12182-016-0084-7
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12182-016-0084-7