Abstract
Development of unconventional shale gas resources involves intensive capital investment accompanying large commercial production uncertainties. Economic appraisal, bringing together multidisciplinary project data and information and providing likely economic outcomes for various development scenarios, forms the core of business decision-making. This paper uses a discounted cash flow (DCF) model to evaluate the economic outcome of shale gas development in the Horn River Basin, northeastern British Columbia, Canada. Through numerical examples, this study demonstrates that the use of a single average decline curve for the whole shale gas play is the equivalent of the results from a random drilling process. Business decision based on a DCF model using a single decline curve could be vulnerable to drastic changes of shale gas productivity across the play region. A random drilling model takes those drastic changes in well estimated ultimate recovery (EUR) and decline rates into account in the economic appraisal, providing more information useful for business decisions. Assuming a natural gas well-head price of $4/MCF and using a 10 % discount rate, the results from this study suggest that a random drilling strategy (e.g., one that does not regard well EURs), could lead to a negative net present value (NPV); whereas a drilling sequence that gives priority to developing those wells with larger EURs earlier in the drilling history could result in a positive NPV with various payback time and internal rate of return (IRR). Under a random drilling assumption, the breakeven price is $4.2/MCF with more than 10 years of payout time. In contrast, if the drilling order is strictly proportional to well EURs, the result is a much better economic outcome with a breakeven price below the assumed well-head price accompanied by a higher IRR.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Recent advances in horizontal drilling coupled with multistage hydraulic fracturing have extended our ability to produce commercial oil and natural gas from low porosity–permeability fine-grained reservoirs. These technical advances have resulted in a fundamental shift in North American energy markets, as illustrated by the fast and large-scale development of shale gas and tight oil (EIA 2014). Although shale gas development projects face various challenges due to the uncertainties of environmental impacts and the long-term sustainability of economic development of this energy resource (Cueto-Felguerosoa and Juanesa 2013; Hughes 2013; Inman 2014), the potential economic benefits in North America have inspired shale exploration activities in other continents (Aguilera and Radetzki 2013; Huang et al. 2012; Jia et al. 2012; Zou et al. 2012), such as China with the recent discovery of the Fuling field, a giant shale gas field in the Sichuan Basin (Zuo et al. 2015). It is likely that many other countries, particularly in Europe where natural gas supply is tight and politically sensitive, will follow North American shale gas development trends (Aguilera and Radetzki 2013; Monaghan 2014; Slingerland et al. 2014; Weijermars 2013).
Bringing shale gas to market involves all aspects of upstream petroleum industry activities, from exploration for, pilot tests of, and commercial production of gas from shale reservoirs in a basin. Many business aspects of conventional petroleum exploration and development have been discussed in the “Business of Petroleum Exploration” edited by Steinmetz (1992). For example, Megill (1992) defined the economics of conventional petroleum exploration to evaluate the economic viability of transforming potential resources to producible reserves for commercial development and he discussed various economic measuring-sticks for supporting decision-making. Development economics refers to the determination of the investment opportunities that occur after the discovery of the resource, with specific regard to the techniques used and the economic yardsticks available for investment decisions (Roebuck 1992). In principle, the economic analysis of unconventional shale gas resources is no different than the economic analysis of conventional petroleum resources. However, because of the very nature of a pervasive regionally occurring, but spatially variable resource density and reservoir characteristics, the development of shale gas is characterized by lower geologic discovery risk, but higher commercial production risk (Gray et al. 2007). The challenge in shale gas plays is not to find where they contain natural gas, but to find the areas that are economically viable, which will lead to the best production and recovery volumes at a rate of return that satisfies investors (Kaiser and Yu 2012). Thus, shale gas economic appraisal has its primary emphasis on development and production evaluation.
Natural gas in shale formations has been known for over a century in North America (Zagorski et al. 2012). Economic evaluation of the feasibility of commercial production of natural gas from shale formation can be traced back many years prior to the shale gas evolution in the early 2000s. For example, TRW (1977) in a scientific report documented the economic side of the Devonian shale gas drilling ventures involving fracturing stimulation of the Appalachian Basin in the United States. In recent years since the start of the shale gas boom, methods and procedures of economic feasibility evaluation of shale gas development have been proposed and examples of economic appraisals of North American shale plays are publically available in literature as well as from industry reports.
Agrawal (2009) conducted an economic analysis on five emerging shale gas plays in the United States for two types of completions—vertical and horizontal to examine which completion method is the best under different economic environments. A discounted cash flow (DCF) model was used to generate economic yardsticks, such as net present value (NPV), internal rate of return (IRR) and payout time for comparing the economic outcomes in those five emerging shale plays. Hammond (2013) also used a DCF model to evaluate shale gas production well economics. He breaks down the breakeven natural gas price by year and shale play to illustrate the variability of economic outcomes in the major North American shale plays. Penner (2013) discussed different input parameters and factors in single well production economic appraisal and illustrated the importance of understanding the range of resource potential for commercial realization. Projection of future production is believed to be one important element in shale gas development economic analysis. Weijermars (2014) presented the uncertainty range in the future natural gas production output from US shale plays up to 2025 using a bottom up model as opposes to the top–down model of the US National Energy Modeling System (NEMS) by EIA (2014).
Kaiser and Yu (2013, 2014) published a series of articles discussing natural gas well production characteristics, operation costs, and economic analysis of the Haynesville Shale in Louisiana. The Haynesville Shale play has been one of the major shale gas plays in the United States. Although technical advances have lowered the development cost constantly, depressed well-head natural gas price is still the main constraint responsible for decline in the number of drilling rigs and production in the region.
Weijermars (2013) discussed economic feasibility of five emergent shale gas plays on the European continent. The study assumes that natural gas production is from 100 wells, drilled over a decade at a rate of 10 wells/year for each shale gas play and that production performance follows an exponential decline similar to the model used by EIA (Cook and Wagener 2014). The specific input parameters for shale gas productivity, such as initial production (IP), decline rate and well EURs in each play are generated by analogy to the production data of well-known shale plays in the United States. By applying the same production decline model to all wells in each shale gas play, the natural gas production from the realized wells over a 25-year life cycle were analyzed using DCF models to generate financial criteria as economic indicators for ranking the relative prospectivity of the five studied shale gas plays. The risks due to uncertainties in resource potential estimates, production performance and fiscal regimes are translated into the uncertainty in cash flow models under different scenarios. The resulting economic outcomes of gas productions in P10, P50, and P90 were presented to represent the uncertainty.
This paper presents a probabilistic model for shale gas development economic evaluation by considering the differences in well EUR and natural gas productivity due to variable geological/reservoir characteristics across a basin. The Horn River shale gas play in western Canada is used as an example to demonstrate the differences in economic outcomes under various financial terms for the same shale gas play.
2 Methods
2.1 Discount cash flow model
DCF analysis values a shale gas development project using the concept of the time value of money (such as inflation and bank interest). All future cash flows are estimated and discounted to give their present values (PVs). The sum of all future cash flows is the NPV, which is taken as the value of the cash flows. NPV, breakeven price, IRR and payout time provide the economic yardsticks for supporting investment decisions. Megill (1992) described the use of cash flow models and NPV to generate economic yardsticks in exploration economic analysis in detail. Weijermars (2013) provides a quantitative description of formulating a DCF model.
The DCF approach involves many aspects in petroleum business, some of which are technical and the others are fiscal terms. All those have to be analyzed and quantified as input parameters. Iledare (2014) discussed different fiscal terms in upstream petroleum economic analysis in the United States.
2.2 Gas price model
The future natural gas price is an external uncertainty factor affecting the revenue and economic margin of natural gas sales. In the last 10 years, well-head prices have been extremely volatile, varying from $2/MCF to over $10/MCF in the North American natural gas market, and is reflective of the regional demand and supply dynamics. In North America, the spot natural gas prices continue to depress the well-head prices of all natural gas producers due to rapid growth of natural gas production from shale gas reservoirs. The cash flow models in this study adopt an initial natural gas price set at $4/MCF, with a forward correction for inflation modeled by an annual inflation factor of 1.5 % using the following equation (Weijermars 2013).
where P n is the well-head natural gas price in year n, P 1 the well-head natural gas price in the 1 year, and r inf the annual inflation rate affecting the natural gas price, and n the number of years of natural gas production. In our models 1000 cubic feet (1 MCF) of natural gas is equivalent to a calorific value of 1 million British thermal units (1 M Mbtu) in market pricing. Alternative functions for modeling natural gas price trends and background on what drives regional natural gas prices are highlighted in EIA (2014) and Weijermars (2013).
2.3 Production decline models
Forecasting long-term natural gas production from shale gas reservoirs is an essential element in economic evaluation. Single well estimated ultimate recovery (EUR) can be estimated directly from historical production data by fitting a decline model (Lee 2012). Among the available models, the Arps model is a well-known model proposed for various conventional reservoirs that has been applied to estimate well EUR for several decades (Arps 1945, 1956; Lee 2012). It has the following form.
where q is the production rate, t the time, q i the IP rate, b and D i are model parameters.
The application of the Arps model (i.e., the exponential and hyperbolic decline relations) is restricted to boundary-dominated flow regimes and may lead to significant overestimation of reserves if it is applied to transient flow (Ilk et al. 2010). Another problem is when in the hyperbolic decline form, the Arps model may lead to a physically impossible result in some cases (Lee 2010).
For a better empirical fit to production from tight reservoirs, like shale gas reservoirs, many new decline models have been proposed in recent years. The Valko model, also called the stretched exponential model, was proposed by Valko and Lee (2010) for unconventional shale gas and tight reservoirs. It is applied commonly to unconventional resource assessment (e.g., Valko and Lee 2010; Lee 2012; Chen and Osadetz 2013). The model has the following form:
where q is the production rate, t the time, q i the IP rate, n and τ are model parameters.
A simple exponential decline function is often used for modeling production decline in many academic and government energy supply analyses (EIA 2014; Cook and Wagener 2014; Weijermars 2013, 2014) with the following form:
where Q 1 is the production in year 1 and decline factor r. The production in year n is given by Q n .
However, the fundamental mechanisms controlling shale gas production remain poorly understood, and the classic theories and simulation techniques used by the oil and natural gas industry have proven inadequate for shale gas reservoirs (Cipolla et al. 2010; Monteiro et al. 2012). Under these circumstances, there is an obvious need for the theoretically based rate-decline models that are applicable for all flow regimes. Ilk et al. (2010) proposed a hybrid model for performance forecasting. The proposed model consists of three main rate-time relations and five supplementary rate-time relations, which utilize power-law, stretched exponential, hyperbolic, and exponential components to properly model the behavior of a given set of rate-time data from unconventional reservoirs.
In a recent study, Patzek et al. (2013) proposed a “diffusion-type” equation to model production decline from shale reservoirs. By introducing physical mechanisms behind natural gas recovery for shale formations to the production rate, this model represents a contribution toward reducing uncertainty (Cueto-Felguerosoa and Juanesa 2013). However, it is conceivable that the conceptual model of a linear, single-phase flow of gas into parallel, equidistant fractures may not be universally applicable. The complexity of induced hydraulically fractured geometries, the stimulation of networks of pre-existing (natural) fractures, adsorption and desorption processes, and non-Darcy multiphase flow through the chemically heterogeneous shale are all phenomena that could potentially result in a departure from the scaling behavior of the Patzek model (Cueto-Felguerosoa and Juanesa 2013).
For this study, the Valko model is used to estimate well EURs and generate production profiles (decline curves) from historical monthly natural gas production records in all the production wells. This is used to represent the anticipated variations in ultimate recoverable resource and production performance throughout the Horn River Basin shale gas play.
3 Horn River example
3.1 Geological background and data
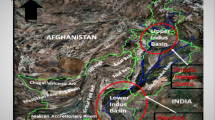
The Horn River Basin, located in northeastern British Columbia (BC) in Canada (Fig. 1), covers about 11,000 km2 (BCOGC 2014). IP wells of 30 MMCF/day (close to 1.0 million m3/day) suggest that the Horn River Basin is one of most proliferous dry gas shale plays in North America. Three organic-rich stratigraphic units of Devonian age are the current targets for shale gas development in the basin (Fig. 2). The thickness of the three units varies from 100 to 300 m with burial depth of around 2500 m. Natural gas production started in 2005 (BCOGC 2014) and historical monthly production data (up to the end of October 2014) from 242 stimulated wells are collected from a commercial dataset. Natural gas composition analysis indicates that the methane content of the natural gas accounts for only 82 %–92 % depending on the stratigraphic units. Other natural gas contents include CO2 and small amount of H2S. Table 1 lists some major parameters of the reservoir, horizontal well and completion in this basin. Table 2 lists the production and financial parameters of the Horn River shale gas play for economic appraisal.
Geological cross section demonstrating the major structural and depositional features of the basin and the target horizons in the Horn River Basin (cross section from Fiess et al. 2013)
Figure 3 shows a histogram and a cumulative probability distribution of well EURs derived from fitting the historical production records of 206 production wells with production longer than 12 months by the Valko model. The EURs vary considerably from less than 3 BCF/well to over 40 BCF/well with a mean of 11.9 BCF/well and a median of 9.9 BCF/well, indicating a drastic variation in productivity across the basin, similar to other North American shale basins (Maugeri 2015).
The natural gas resource evaluation of the Horn River Basin was conducted by a joint effort from the British Columbia Ministry of Energy and Mines and the National Energy Board (2011) using a volumetric approach. Chen and Osadetz (2015) conducted a natural gas resource assessment of the Horn River Shale Basin using historical production data. The estimated recoverable natural gas resource potential varies from 32 TCF to 235 TCF (90 %–10 % confidence interval) with a median 118 TCF. The estimated number of production wells required to drain all the recoverable resource was estimated from a few thousand to over twenty thousand.
The North America natural gas price has been fluctuated between $2.5/MCF and $10/MCF in the last 20 years. We assume a start well-head price of US$4/MCF with an annual inflation adjustment of 1.5 % (Fig. 4) in this study and a comparison of the natural gas price used in this study with the projected future North America natural gas price by EIA (2013) is provided in Fig. 4.
Comparison of the EIA forecast natural gas price (EIA 2013) and the model used in this study
3.2 Single well development economics
To illustrate the workflow of the economic analysis and method, the economic evaluation of a single production well with fixed financial and fiscal terms is conducted using the DCF method. The capital expenditures (CAPEX), operational expenses (OPEX) and other expenses and fiscal terms are listed in Table 2. Figure 5 is a typical production curve fitted to a decline model using the Valko model (200/C-096-H 094-O-08/00 well), showing general characteristics of well performance of the Horn River shale gas play. A projection of the fitted decline curve from the Valko model for 40 years of production lifetime gives a well EUR of 10.9 BCF/well, which is close to the mean value of 11.9 BCF/well for all the 206 production wells. Figure 6a shows monthly and cumulative natural gas sales and Fig. 6b shows the cumulative present value of cash flows under different discount rates with a payback period of about 11 years. With current fiscal terms and economic condition, any scenarios with a discount rate >7 % will not generate positive NPV (Fig. 6c). Given a discount rate of 10 %, the NPVs with different natural gas well-head prices is shown in Fig. 6d, suggesting that under this discount rate, only with a well-head price greater than $4.2/MCF does the NPV become positive (breakeven price). When the well EUR is greater than 17 BCF/well, the model indicates a positive NPV (Fig. 6e). Any production well with EUR < 10 BCF needs more than 10 years to pay back the investment (Fig. 6f) under the scenario of well-head price at a given discount rate of 10 %.
Economic appraisal results from the DCF model based on a single well shale gas development project. Monthly production and cumulative production curve (a), PV of cumulative cash flow with different discount rates (b), discount rate against NPV (c), gas initial price against NPV (d), well EURs against NPV (e), and well EURs against payout time with a discount rate of 10 % (f)
3.3 Shale gas play development economics
Chen and Osadetz (2015) estimated that it may need at least eight thousand production wells to exhaust the natural gas resource in the Horn River shale gas play. To discuss the shale gas development economics, we assume that a total of 1440 wells are to be drilled in the next 20 years with a drilling rate of six wells/month with a production lifetime of 40 years for each production well. The same economic and fiscal terms used for the single production well case study are applied. In the shale gas development economic analysis, we present two scenarios of utilizing a simple mean production decline model and a random drilling process to illustrate the advantages of including full range of variations in well EUR and production decline on economic outcomes of the same shale gas play.
3.3.1 Average production decline model
A single decline curve derived by averaging the 206 decline models derived from the production wells is used to represent the average natural gas productivity of the Horn River play. The cumulative natural gas production of continuous drilling shows rapid increase of natural gas production with time and reaches the maximum production capacity at the end of 20 years when the last production well completed starts producing gas (Fig. 7a). A rapid decline of gas production follows because of the fast depletion of gas in the vicinity of the hydraulic fracture networks in the fractured horizontal wells such that the decline rate gradually becomes flatter with time (Fig. 7a). The production rate drops again at 40 years as the oldest production wells come to the end of their production lifetime. The discounted cash flow model with a discount rate of 10 % suggests no positive NPV even though the model generated large amounts of cash, as most of the positive cash flow occurs after 20 years of production (Fig. 7b).
Economic evaluation results at a play level based on a total of 1440 wells with a drilling rate of 6 wells/month. Production (monthly and cumulative) curves with time under the scenario of a single average decline production model (a), PV of cumulative discount cash flow model (discount rate = 0: solid; discount rate = 10 %: dashed) (b), production curves based on a random drilling model (c), PV of cumulative discount cash flows of the random drilling model (discount rate = 0: solid; discount rate = 10 %: dashed) (d)
3.3.2 Random drilling scenario
It is interesting to compare the above-mentioned discount cash flow model using a single average production decline curve with a model using a random drilling procedure. A random drilling procedure can represent the full variation in the well EUR and production decline on the economic outcome. For the random sampling model, the following assumptions are made:
-
1.
The historical production data from the 206 production wells represent a sample from a parent population of all possible natural gas production outcomes.
-
2.
The 206 production decline curves derived from fitting the Valko model to the historical production data are extended to 40-year production lifetime to represent the production performance of the wells in the Horn River shale.
-
3.
A minimum of 8000 wells are required to extract the shale gas resource in the Horn River Basin.
A random drilling procedure means that a well with any given value of EUR could appear at any order in a drilling sequence. Thus, there are many equally probable combinations that can form a random drilling sequence. To capture all possible outcomes, Monte Carlo simulation is used to generate drilling sequences randomly. A total of 2000 equal probable drilling sequences (also called random realizations) were generated and each of the drilling sequences has 1440 production wells. The effect of many equally possible combinations of drilling sequences on economic outcomes can be captured by analyzing the results of the 2000 repeated random realizations. Figure7c shows the average gas production from the 2000 random drilling sequences. Except for a rougher gas production curve (Fig. 6a), the rest of the curves looks similar (Fig. 7a, c). Figure 7d shows the mean cash flows with and without discount by averaging 2000 modeled outcomes from the random drilling development plan and the results suggest no positive NPV with a 10 % discount rate. It is no surprise that the two discount models in Fig. 7b, d have the same outcomes. This is because the average of a random sample is equivalent to the mean of the population. However, the random sampling procedure produces more than a mean, and other statistical measures provide the uncertainty or variation of the possible outcome, yielding more information for business decisions (Fig. 8a), from which it is clear that under the assumed economic and fiscal terms, a random drilling development strategy does not result in a positive NPV unless the well-head gas price is higher than $4.3/MCF (Fig. 8b), or the average well EUR is greater than 15 BCF/well. In this case, only if the discount rate is lower than 7 %, the NPV is expected to be positive (Fig. 8e).
Economic outcomes of the discounted cash flow models plotted as mean, p05 and p95 from Monte Carlo simulation of 2000 equally probable realizations under a random drilling scenario (a) and other diagrams showing the economic measures for the Horn River Basin shale gas development strategies. Initial natural gas price versus NPV (b), well EUR versus NPV (c), well EUR versus payback time under a discount rate of 10 % (d), discount rate versus NPV; and initial gas price versus payback time under a discount rate of 10 % (f)
3.3.3 When someone does better than the average
In fact, one may do things better than others. Depending on the technology applied, the understanding of the rock or early entry of the play, some companies can do better than average, which means that a better gas recovery from the same shale formation can be achieved. Owning the best acreage or the worst makes a huge difference in economic outcomes (Maugeri 2015). If information on potential size of well EURs for selecting drilling sites is available, an optimal development strategy can be planned. By drilling sweet spots with higher productivity than an average EUR in the early stage of shale gas development, better economic outcomes can be achieved. To illustrate this effect, we generated drilling sequences better than average statistically based on a sampling scheme adopted from “discovery process” models (Andreatta and Kaufman 1996; Chen et al. 2013), commonly used in conventional petroleum resource assessment. Such a drilling sequence, which is affected by, but not exactly ranked by well EUR, is of probabilistic character in nature. The possible drilling sequence is formulated using the probabilistic model as a result of sampling from the parent population with a probability proportional to well EUR without replacement (Andreatta and Kaufman 1996). This probabilistic model and its application have been presented by Chen and Osadetz (2015) and will be discussed elsewhere in a separate paper.
Following the same development plan as applied to the random drilling scenario, a total of 1440 wells are drilled in 20 years and 2000 equally probable realizations of drilling sequences were generated to represent the possible combinations wells with different EURs and decline rates in the drilling sequence. After 60 years drilling and production (20 years drilling program and 40-year production), 22 TCF of natural gas was sold (Fig. 9a). This scenario resulted in an average drilled well EURs of 17.5 BCF/well, much higher than the mean of 11.7 BCF/well of all 206 production wells. Under the same fiscal and economic terms, it gives a mean NPV of $2.6 billion Canadian dollars at the end of 60 years (Fig. 9b, c). Compared to the previous random or average production scenarios, this approach results in better economic outcomes given the lower breakeven price and higher IRR. The internal return rate is 14 % (Fig. 9d), the breakeven price is only $3.2/MCF (Fig. 9g) and the payback time is about 13 years (Fig. 9b).
Economic outcome forecasting of the discounted cash flow models from 2000 Monte Carlo simulations for the selective drilling strategy with probability proportional to well EUR in Horn River Basin. Natural gas production with time (a), PV of cumulative cash flow plot with two different discount rates (disc. rate = 0: solid line; disc. rate = 10 %: dashed line) (b), mean, p05 and p95 of PV of cumulative discount cash flow (disc. rate = 10 %) from 2000 equal probable Monte Carlo simulations (c), discount rate versus NPV (d), well EUR versus NPV (e), and initial natural gas price versus payback time under 10 % discount rate (f)
4 Conclusions
The current practice of shale gas economic evaluation commonly uses a mean EUR and a single production decline model for the entire lease or play (e.g., Penner 2013; Weijermars 2013; Cook and Wegener 2014). Through numerical examples, this study shows that the use of a single average decline curve for the whole shale gas play is equivalent to a random drilling process. Business decisions based on economic forecasting derived from a single decline curve could be vulnerable to drastic changes of shale gas productivity across the region. While the random drilling model, taking account of variable well EURs and decline rates in economic appraisal, can result in large variation in economic outcomes and more statistical measures, it is useful for various business decisions, risk aversion and alternative development strategy planning.
Shale gas development drilling is based on pre-screening criteria and appears to be selective for potentially high productivity. A random drilling model may not fully capture the dynamic resource development process. To illustrate the impact of a selective drilling program on the economic outcome, a better than average drilling scenario is used in the DCF model. Under the assumed fiscal and economic terms, this study indicates that a shale gas resource development strategy with a random drilling strategy most likely results in, a negative NPV with a breakeven price of $4.2/MCF. However, under a selected drilling strategy, where the order of drilling is affected by well EUR, the economic outcome is improved with the breakeven price dropping below the well-head gas price and resulted in more than a 10 % IRR. This may imply that early identification of and drilling on “sweet spots” is critical to success in shale gas development.
Abbreviations
- BC:
-
British Columbia
- BCF:
-
One billion cubic feet
- BCOGC:
-
British Columbia Oil and Gas Commission
- DCF:
-
Discount cash flow
- EIA:
-
Energy Information Administration (US)
- EUR:
-
Estimated ultimate recovery
- IRR:
-
Internal rate of return
- MBTU:
-
Thousand British thermal units
- MCF:
-
Thousand cubic feet
- MMCF:
-
Million cubic feet
- NPV:
-
Net present value
- PVs:
-
Present values
- TCF:
-
Trillion cubic feet
References
Agrawal A. A technical and economic study of completion techniques in five emerging US gas shale plays. Master of Science thesis, Texas A&M University; 2009.
Aguilera RF, Radetzki M. Shale gas and oil: fundamentally changing global energy markets. Oil Gas J. 2013;111(12):54–61.
Andreatta G, Kaufman G. Estimation of finite population properties when sampling is without replacement and proportional to magnitude. J Am Stat Assoc. 1996;81(395):657–66.
Arps JJ. Analysis of decline curves. Trans AIME. 1945;160:228–47.
Arps JJ. Estimation of primary oil reserves: transactions AIME. J Petrol Technol. 1956;207:182–91.
British Columbia Ministry of Energy and Mines and National Energy Board, 2011. Ultimate potential for unconventional natural gas in northeastern British Columbia’s Horn River Basin; Oil and Gas Reports 2011-1, 39 p. https://www.neb-one.gc.ca/nrg/sttstc/ntrlgs/rprt/archive/ncnvntnlntrlgshrnrvrbsnhrnrvr2011/ncnvntnlntrlgshrnrvrbsnhrnrvr2011-eng.pdf
British Columbia Oil and Gas Commission (BCOGC). Horn River Basin unconventional shale gas play Atlas. 2014. http://www.google.ca/url?url=http://www.bcogc.ca/node/11238/download&rct=j&frm=1&q=&esrc=s&sa=U&ei=N-ihVOyZM4WhyASky4CoBg&ved=0CCMQFjAB&sig2=xX6DE2ZvElbdjpTXe2bTLw&usg=AFQjCNH_CEuFPdrCKO6jtHtD0aADdyFDsA.
Chen Z, Osadetz KG. Characteristics and resource potential evaluation of tight oil resources in Upper Cretaceous Cardium Formation, Western Canada Sedimentary Basin. Pet Explor Dev. 2013;40(3):344–53.
Chen Z, Osadetz KG. Economic implications of drilling sequence in shale gas development, example from Horn River Basin, Canada. GeoConvention, May 4–8, 2015, Calgary, Alberta.
Chen Z, Osadetz K, Chen G. Application of a least square non-parametric discovery process model to Colorado group mixed conventional and unconventional oil plays, Western Canada sedimentary basin. In: Pardo-Iguzqiza E, Guardiola-Albert C, Heredia J, Moreno-Merino L, Duran JJ, Vargas-Guzman JA, editors. Proceedings of the fifteenth annual conference of the international association for mathematic geosciences. New York: Springer; 2013. p. 617–20.
Cipolla CL, Lolon EP, Erdle JC, et al. Reservoir modeling in shale-gas reservoirs. SPE Reserv Eval Eng. 2010;13:638–53.
Cook T, Wagener DV. Improving well productivity based modeling with the incorporation of geologic dependencies. EIA, working paper series; 2014.
Cueto-Felguerosoa L, Juanesa R. Forecasting long-term gas production from shale. Proc Natl Acad Sci USA. 2013;110(49):19660–1.
EIA. Annual energy outlook 2013. DOE/EIA-0383(2013), June 2011. US Department of Energy, Energy Information Administration, Washington, DC; 2013. http://www.eia.gov/forecasts/aeo/pdf/0383(2013).pdf.
EIA. Annual projections to 2040. Updated data series. 2014. http://www.eia.gov/forecasts/aeo/pdf/tbla13.pdf.
Fiess K, Ferri F, Pyle L, et al. Liard Basin hydrocarbon project: shale gas potential of Devonian-Carboniferous strata in the Northwest territories, Yukon and northeastern British Columbia.GeoConvention 2013, extended abstract, Canadian Society of Petroleum Geologists. 2013. http://cseg.ca/assets/files/resources/abstracts/2013/263_GC2013_Liard_Basin_Hydrocarbon_Project.pdf.
Gray WM, Hoefer TA, ChiappeA, et al. A Probabilistic approach to shale gas economics, SPE-108053-MS. 2007. doi:10.2118/108053-MS
Hammond CD. Economic analysis of shale gas wells in the United States batchelor’s thesis. Massachusetts Institute of Technology. 2013. http://dspace.mit.edu/handle/1721.1/83718#files-area.
Huang J, Zou C, Li J, et al. Shale gas generation and potential of the lower Cambrian Qiongzhusi Formation in Southern Sichuan basin. China Pet Explor Dev. 2012;39(1):69–75.
Hughes JD. Energy: a reality check on the shale revolution. Nature. 2013;494:307–8. doi:10.1038/494307a.
Iledare OO. Upstream petroleum economic analysis: balancing geologic prospectivity with progressive, stable fiscal terms and instruments. Way Ahead. 2014;10(1):28–30.
Ilk D, Currie, SM, Symmons D, et al. Hybrid rate-decline models for the analysis of production performance in unconventional reservoirs, SPE 135616. Prepared for presentation at the SPE annual technical conference and exhibition held in Florence, Italy, September 19–22, 2010.
Inman M. The fracking fallacy. Nature. 2014;516(4):28–30.
Jia C, Zheng M, Zhang Y. Unconventional hydrocarbon resources in China and the prospect of exploration and development. Pet Explor Dev. 2012;39(2):129–36.
Kaiser MJ, Yu Y. Louisiana Haynesville shale—2: economic operating envelopes characterized for Haynesville shale. Oil Gas J. 2012; 110(1a):70–74, 87.
Kaiser MJ, Yu Y. Haynesville update—1: north Louisiana gas shale’s drilling decline precipitous. Oil Gas J. 2013; p. 62.
Lee WJ. Gas reserves estimation in resource plays. SPE paper 130102, presented at the unconventional gas conference, Pittsburgh, Pennsylvania, USA, February 23–25, 2010.
Lee WJ. Production forecast, reserves estimations and reporting rules for unconventional resources. Course material of SPE training series, hold in conjunction with SPE Canadian unconventional resources conference, Calgary AB, Canada, October 28–29, 2012.
Maugeri L. Comment: beware of break-even and marginal-cost analyses. Oil Gas J. 02/10/2015. http://www.ogj.com/articles/uogr/print/volume-3/issue-1/comment-beware-of-break-even-and-marginal-cost-analyses.html.
Megill RE. Exploration economics: chapter 10: part III. Economic aspects of the business. In: Steinmetz R, editor. The business of petroleum exploration, AAPG treatise of petroleum geology handbook of petroleum geology, vol 2. 1992. p. 107–16.
Monaghan AA. The carboniferous shales of the midland valley of Scotland: geology and resource estimation. British Geological Survey for Department of Energy and Climate Change, London, UK. 2014.
Monteiro PJM, Rycroft CH, Barenblatt GI. A mathematical model of fluid and gas flow in nanoporous media. Proc Natl Acad Sci USA. 2012;109(50):20309–13.
Patzek TW, Male F, Marder M. Gas production in the Barnett shale obeys a simple scaling theory. Proc Natl Acad Sci USA. 2013;110:19731–6.
Penner E. Shale gas production economics spreadsheet model and inputs. Oil Gas Financ J. September 20, 2013. http://www.ogfj.com/articles/2013/09/shale-gas-production-economics-spreadsheet-model-and-inputs.html.
Roebuck F. Development economics. In: Steinmetz R, editor. 382p. ISBN 0-89181-601-1. p. 117–24. American Association of Petroleum Geologists, Tulsa; 1992
Slingerland S, Rothengatter N, van der Veen R, et al. Economic impacts of shale gas in The Netherlands. http://www.tripleeconsulting.com/sites/default/files/Economic%20Impacts%20of%20Shale%20Gas%20in%20the%20Netherlands%20-%20FINAL%20REPORT.pdf.2014.
Steinmetz R. The business of petroleum exploration, AAPG treatise of petroleum geology handbook of petroleum geology, vol 2. American Association of Petroleum Geologists: USA; 1992.
TRW. Economic analysis of Devonian gas shale drilling ventures involving fracture stimulation, a report prepared for the United States Department of Energy, under contract EY-77-C-2 l-8085.1977. http://www.netl.doe.gov/kmd/cds/disk7/disk1/EGS%5CEconomic%20Analysis%20of%20Devonian%20Gas%20Shale%20Drilling%20Ventures%20In.pdf.
Valko PP, Lee WJ. A better way to forecast production from unconventional gas wells. SPE J. 2010;2(3):134–231.
Weijermars R. Economic appraisal of shale gas plays in continental Europe. Appl Energy. 2013;106:100–15. http://www.alboran.com/files/2013/07/SR-7.pdf.
Weijermars R. US shale gas production outlook based on well roll-out rate scenarios. Appl Energy. 2014;124:283–97.
Zagorski WA, Wrightsone GR, Bowman DC. The Appalachian Basin Marcellus gas play: its history of development, geological controls on production, and future potential as a world-class reservoir. In: Breyer JA, editor. Shale reservoirs—giant resources for the twenty-first century AAPG Memoir. 2012;97:172–200.
Zou C, Yang Z, Tao S, et al. Nano-hydro-carbon and the accumulation in coexisting source and reservoir. Pet Explor Dev. 2012;39(1):15–32.
Zuo C, Zhai G, Zhang G, et al. Formation, distribution, potential and prediction of global conventional and unconventional hydrocarbon resources. Pet Explor Dev. 2015;42(2):13–25.
Acknowledgments
The study is funded partly by the ecoEII program and supported by Geoscience for New Energy Supply Program of Natural Resources Canada. The authors thank internal reviewer Dr. Stephen Grasby of the Geological Survey of Canada and journal reviewer Dr. Keyu Liu for their helpful comments and suggestions. This is ESS contribution #20150145.
Author information
Authors and Affiliations
Corresponding author
Additional information
Edited by Xiu-Qin Zhu
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Chen, Z., Osadetz, K.G. & Chen, X. Economic appraisal of shale gas resources, an example from the Horn River shale gas play, Canada. Pet. Sci. 12, 712–725 (2015). https://doi.org/10.1007/s12182-015-0050-9
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12182-015-0050-9