1 Introduction

Fracture is the smallest and the most complex structure in the crust. It can not only increase the pore space and permeability, but also control the formation, distribution, and capacity of oil and gas in place (Jiang et al. 2004; Zeng et al. 2007; Zhang et al. 2009; Weng et al. 2011; Nie et al. 2012; Kuchuk and Biryukov 2014; Reynolds et al. 2014; Yao et al. 2013; Zhao et al. 2014). Fracture identification and quantitative characterization are keys to effective exploration of fractured reservoirs (Bourbiaux 2010; Sun et al. 2011). Dual laterolog is widely used to study fracture development and fracture porosity because of good current focusing and detectability of fractured formation (Sibbit and Faivre 1985; Li et al. 1996; Deng and Li 2009; Noroozi et al. 2010; Le et al. 2011; Ja’fari et al. 2012; Deng et al. 2013). However, dual laterolog cannot accurately reflect complex heterogeneity and anisotropy in fractured reservoirs. Formation MicroScanner Image (FMI) figures can provide visual displays of sidewall geological characteristics of fractures, caves, etc. But shallow investigation depth limits its further application (Shen et al. 2009; Dershowitz et al. 2010; Sausse et al. 2010; Yang et al. 2011; Deng et al. 2012; Moinfar et al. 2010; Yun et al. 2013). Azimuthal resistivity imager (ARI) and high-resolution azimuthal laterolog sonde (HALS) were earlier proposed to study three-dimensional distribution of resistivity surrounding the borehole. However, the logging response mechanism is not well understood and application examples about fractures are rare (Faivre 1993; Davies et al. 1994; Smits et al. 1995; Yang and Tao 1999; Karim et al. 2013; Olsen et al. 2014). This study aims to implement numerical simulation of the high-resolution azimuthal resistivity laterolog (HARL), in order to combine the radial detection of dual laterolog and azimuthal detection around the borehole, and then corresponding logging response characteristics and identification method of fractures are investigated to aid fractured reservoir evaluation.

2 Three-dimensional finite element model of fractured reservoirs

2.1 Fundamental theory

HARL can provide two measurement modes, high-resolution dual laterolog mode and azimuthal resistivity measurement mode. As shown in Fig. 1, differing from the conventional dual laterolog, the main current electrode of high-resolution dual laterolog mode is divided into A0 and A0′, and then an electrical potential guiding electrode (M0) is added between A0 and A0′. According to the potential difference of three electrical potential guiding electrodes, the instrument constantly adjusts the focusing voltage. This configuration not only improves the vertical resolution, but also significantly reduces the instrument length. Azimuthal resistivity measurement mode is achieved by the electric potential difference between 12 azimuthal electrodes disposed in the electrical potential guiding ring (M0). The angle of a single azimuthal electrode is 10°. The angle between the center axes of two adjacent azimuthal electrodes is 30°. Therefore, the HARL can simultaneously measure high-resolution dual laterolog and azimuthal resistivity and then obtain two images of shallow and deep investigation depth, respectively.

Fig. 1
figure 1

High-resolution azimuthal resistivity laterolog

Full size image

High-resolution dual laterolog mode sets the electrical potential equal between the average value of 12 azimuthal electrodes and the two electrical potential guiding electrodes (M1, M1′), then the expression formulas of high-resolution dual laterolog mode are obtained as follows:

$${\text{HARLd}} = K_{\text{d}} \frac{{U_{{{\text{d}}({\text{M1}})}} }}{{I_{{{\text{d}}({\text{A}}0)}} + I_{{{\text{d}}({\text{A}}0')}} }}$$
(1)
$${\text{HARLs}} = K_{\text{s}} \frac{{U_{{{\text{s}}({\text{M}}1)}} }}{{I_{{{\text{s}}({\text{A}}0)}} + I_{{{\text{s}}({\text{A}}0')}} }}.$$
(2)

Based on the potential difference between the main current electrode and the 12 azimuthal electrodes, the expression formulas of azimuthal resistivity measurement mode can be obtained as follows:

$${\text{HARLd}}(i) = K_{\text{d}} \frac{{U_{{{\text{d}}({\text{M}}1)}} }}{{I_{{{\text{d}}({\text{A}}0)}} + I_{{{\text{d}}({\text{A}}0')}} }}\frac{{\sum\nolimits_{i = 1}^{12} {\Delta U_{{{\text{d}}({\text{M}}0_{i} {\text{A}}0)}} } }}{{12\Delta U_{{{\text{d}}({\text{M}}0_{i} {\text{A}}0)}} }} \quad i = 1, \, 2, \ldots ,12$$
(3)
$${\text{HARLs}}(i) = K_{\text{s}} \frac{{U_{{{\text{s}}({\text{M}}1)}} }}{{I_{{{\text{s}}({\text{A}}0)}} + I_{{{\text{s}}({\text{A}}0')}} }}\frac{{\sum\nolimits_{i = 1}^{12} {\Delta U_{{{\text{s}}({\text{M}}0_{i} {\text{A}}0)}} } }}{{12\Delta U_{{{\text{s}}({\text{M}}0_{i} {\text{A}}0)}} }} \quad i = 1, \, 2, \ldots ,12,$$
(4)

where K d and K s are coefficients of instrument in deep and shallow laterologs; U d(M1) and U s(M1) are potential values of electrical potential guiding electrode (M1) in deep and shallow laterologs; I d(A0), I s(A0), I d(A0′), and I s(A0′) are current values of main current electrodes (A0, A0′) in deep and shallow laterologs; \(\Delta U_{{{\text{d(M0}}_{i} {\text{A0)}}}}\) and \(\Delta U_{{{\text{s(M0}}_{i} {\text{A0)}}}}\) are potential difference between main current electrodes (A0, A0′) and the azimuthal electrode (M0 i ) in deep and shallow laterologs, respectively.

2.2 Calculation principle

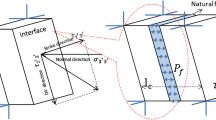
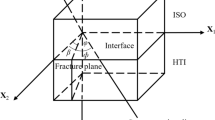
Assuming that a fractured reservoir consists of fractures and bedrock and that the fractures exist in the form of fracture groups, we use the plane model of parallel fractures (Zeng et al. 2007). As shown in Fig. 2, the conductivities of bedrock and fracture fluid are \(\sigma_{\text{b}}\) and \(\sigma_{\text{f}}\) and the aperture and dipping angle of each fracture are h and Ω, respectively. The response of HARL is a comprehensive effect of all media, including fractures and bedrock within the detection range. Assuming that the potential distribution generated by HARL around the borehole is U, the potential gradient of bedrock can be expressed as \(\nabla U\), and the potential gradient in any fracture plane can be decomposed into a normal component (\(\varvec{E}_{\text{bn}}\)) and a tangential component (\(\varvec{E}_{\text{bt}}\)), which are given by

$$\varvec{E}_{\text{bn}} = \varvec{e}_{\text{n}} ( - \nabla U \cdot \varvec{e}_{\text{n}} )$$
(5)
$$\varvec{E}_{\text{bt}} = ( - \nabla U \cdot \varvec{e}_{\text{t}} + \varvec{e}_{\text{n}} (\nabla U \cdot \varvec{e}_{\text{n}} ) \cdot \varvec{e}_{\text{t}} ) \cdot \varvec{e}_{\text{t}} ,$$
(6)

where \(\varvec{e}_{\text{n}}\) is the normal direction of the fracture plane and \(\varvec{e}_{\text{t}}\) is the tangential direction of the fracture plane. Because the normal component of the current and the tangential component of the potential in both sides of the fracture plane are continuous, the current density (\(\varvec{J}_{\text{f}}\)) of fracture part can be decomposed into normal (\(\varvec{J}_{\text{fn}}\)) and tangential (\(\varvec{J}_{\text{ft}}\)) components which are given by

$$\varvec{J}_{\text{fn}}\,=\,\sigma_{\text{b}} \varvec{e}_{\text{n}} ( - \nabla U \cdot \varvec{e}_{\text{n}} ) = \sigma_{\text{b}} (U_{x} \sin \varOmega - U_{z} \cos \varOmega )\varvec{e}_{\text{n}}$$
(7)
$$\varvec{J}_{\text{ft}} { = }\sigma_{\text{f}} [ - \nabla U - (U_{x} \sin \varOmega - U_{z} \cos \varOmega )\varvec{e}_{\text{n}} ].$$
(8)

The formula of using the three-dimensional finite element method to simulate the logging response is given below:

$$\varPhi = \frac{1}{2}\iiint\limits_{V} \,{\varvec{J} \cdot \varvec{E}{\text{d}}x{\text{d}}y{\text{d}}z} - \sum\limits_{E} {U_{E} I_{E} } ,$$
(9)

where \(\varPhi\) is the energy functional, V is the area of the three-dimensional space minus the electrode system, \(U_{E}\) is the potential of all electrodes, and \(I_{E}\) is the supply current. According to Eqs. (5)–(9), the functional equations of HARL in fractured formations can be written as

$$\varPhi = \varPhi_{\text{b}} + \varPhi_{\text{f}} - \sum\limits_{E} {U_{E} I_{E} }$$
(10)
$$\varPhi_{\text{f}} = \frac{1}{2}\iiint\limits_{{V_{\text{f}} }} {[(\sigma_{\text{b}}^{2} /\sigma_{\text{f}} - \sigma_{\text{f}} )( - U_{x} \sin \varOmega + U_{z} { \cos }\varOmega )^{2} + \sigma_{\text{f}} (\nabla U)^{2} ]{\text{d}}V_{\text{f}} }$$
(11)
$$\varPhi_{\text{b}} = \frac{1}{2}\iiint\limits_{{V_{\text{b}} }} {\sigma_{\text{b}} (\nabla U)^{2} {\text{d}}V_{\text{b}} },$$
(12)

where the integration function of \(\varPhi_{\text{b}}\) is only in bedrock and the integration function of \(\varPhi_{\text{f}}\) is only in fractures. Generally, \(\phi_{\text{f}} << 1\) and \(\sigma_{\text{f}} >> \sigma_{\text{b}}\) are established for fracture porosity and fracture fluid conductivity in fractured reservoir, respectively. So Eq. (12) can be written as

$$\begin{aligned} \varPhi = \frac{1}{2}\iiint\limits_{V}\, {[(\sigma_{\text{b}} + \sigma_{\text{f}} \phi_{\text{f}} \cos^{2} \varOmega )(U_{x} )^{2} + (\sigma_{\text{b}} + \sigma_{\text{f}} \phi_{\text{f}} )](U_{y} )^{2} +\,(\sigma_{\text{b}} + \sigma_{\text{f}} \phi_{\text{f}} \sin^{2} \varOmega )(U_{z} )^{2} + } \hfill \\ \, 2\sigma_{\text{f}} \phi_{\text{f}} \sin \varOmega\,{ \cos}\varOmega\, U_{x} U_{z} ]{\text{d}}x{\text{d}}y{\text{d}}z - \sum\limits_{E} {U_{E} I_{E} } \hfill \\ \end{aligned} ,$$
(13)

where \(\phi_{\text{f}}\) is the fracture porosity. According to Eq. (13) and the specific boundary conditions, we can use an improved frontal solver to rapidly calculate the response of HARL (Zhang 1984).

3 HARL response of fracture intersecting borehole

3.1 Calculation condition

The borehole diameter is 8 inches. Mud resistivity is 1 Ω m. Fracture fluid resistivity is 1 Ω m. The numerical simulation model is axisymmetric. So we only observe six azimuthal resistivity curves, and the other six azimuthal resistivity curves are symmetrical about the symmetry plane. As shown in Fig. 2, the positive direction of the x-axis is set as the initial direction of the zero degree angle, and then the measured angle of the 1st–6th azimuthal resistivity successively increases. Because the response characteristics of deep and shallow azimuthal resistivities are similar, except in special circumstances, the article only shows deep azimuthal resistivity.

Fig. 2
figure 2

Fractured reservoir model

Full size image

3.2 Relationship of HARL response and fracture dipping angle

The relationship of HARL response and different fracture dipping angles is shown in Fig. 3a, b, in which the fracture aperture is 50 μm and the bedrock resistivity is 10,000 Ω m. Negative separations between the deep and shallow resistivity occur in low-angle fractures, while positive separations occur in high-angle fractures. As the fracture dipping angle increases, the apparent resistivity and the variation of azimuthal resistivity increase. The 3rd and 4th azimuthal resistivity become the lowest when the two azimuthal electrodes are close to the fracture strike direction. The 1st and 6th azimuthal resistivity become the highest when the two azimuthal electrodes are close to the fracture dipping direction. The results indicate that high-resolution dual laterolog curves can reflect the fracture dipping angle, and azimuthal resistivity curves contain information of the fracture dipping direction.

Fig. 3
figure 3

Relationship of HARL response and different fracture dipping angles. a high-resolution dual laterolog curves, b deep azimuthal resistivity curves

Full size image

3.3 Relationship of HARL response and fracture aperture

The relationship of the apparent resistivity in high-resolution dual laterolog mode and different fracture aperture is shown in Fig. 4a. As the fracture aperture increases, the apparent resistivity decreases. The decrease rate is larger for horizontal fractures than for vertical fractures. So the apparent resistivity of low-angle fractures is obviously lower than that of high-angle ones with the same fracture aperture. When the fracture aperture is large, there are negative separations for low-angle fractures and positive separations for high-angle fractures. The corrected apparent conductivity means the part of the bedrock conductivity minus the logging apparent conductivity. As shown in Fig. 4b, the bedrock resistivity is 3000 Ω m, and the dipping angles are respectively 0°, 45°, and 90°. The corrected apparent conductivities of deep and shallow laterologs are almost linearly related to the fracture aperture. Apparent conductivities increase as the fracture aperture increases. The conductivity of the horizontal fracture is large; in terms of dual laterolog, the response is stronger for low-angle fractures than for high-angle fractures. The deep conductivity is larger than the shallow conductivity for low-angle fractures, while for high-angle fractures the results are opposite. The bigger the fracture aperture is, the larger the separation between the deep and shallow conductivities becomes.

Fig. 4
figure 4

Relationship of HARL response and different fracture aperture. a High-resolution dual laterolog curves, b corrected conductivities of high-resolution dual laterolog curves, c deep azimuthal resistivity curves, d shallow azimuthal resistivity curves

Full size image

The relationship of azimuthal resistivity curves and different fracture dipping angles is shown in Fig. 4c, d. The azimuthal resistivity curves of horizontal fractures are completely overlapped. The variation of azimuthal resistivity becomes larger as the fracture aperture and the fracture dipping angle increase, which reaches maximum as the fracture dipping angle reaches 90°.

3.4 Azimuthal resistivity imaging of fractures

The azimuthal resistivity imaging of fractures with different dipping angles is shown in Fig. 5a. From top to bottom, fracture dipping angles are respectively 0°, 45°, and 75°; the bedrock resistivity is 3000 Ω m; and the fracture aperture is 200 μm. As the fracture dipping angle increases, the bending degree of sine curves becomes bigger and the apparent aperture of fractures becomes larger. When the aperture of fractures is small, the identification of fractures, especially high-angle fractures, becomes challenging, as shown in Fig. 5b, in which the aperture of fractures reduces to 5 μm with the same other conditions as in Fig. 5a.

Fig. 5
figure 5

Deep azimuthal resistivity imaging of fractures with different dipping angles. a Fracture aperture 200 μm, b fracture aperture 5 μm

Full size image

When using the azimuthal resistivity to identify fractures, low-angle fractures can be identified by the decreased amplitude of apparent resistivity, and high-angle fractures can be identified by the variation of azimuthal resistivity. Assuming that the resistivity ratio of bedrock and fracture fluid is 3000:1, for low-angle fractures, the smallest detectable aperture can be less than 10 μm when we set 10 % (the dotted line in Fig. 6a) as an identification threshold in terms of the ratio of the resistivity of the fracture and the bedrock (the formula in Fig. 6a). For high-angle fractures, the smallest detectable aperture can be larger than 10 μm in terms of the ratio of the maximum variation of the azimuthal resistivity and the laterolog resistivity (the formula in Fig. 6b). For medium-angle fractures, the smallest detectable aperture is also larger than 10 μm considering both resistivity amplitude difference and azimuthal variation, as the formulas and the dotted lines shown in Fig. 6c, d. When the resistivity ratio increases to 10,000:1, according to all the solid lines shown in Fig. 6, the detectable aperture becomes smaller. When the fracture aperture is large enough, the maximum variation no longer significantly increases and even decreases for medium-angle and high-angle fractures, as shown in Fig. 6b, d. The spatial resolution of the FMI-HD tool is 0.2 in (5.08 mm), representing the button size of each electrode. But the high-resolution electrodes are sensitive enough to identify fluid-filled fractures less than 10 μm in width.

Fig. 6
figure 6

Determine the smallest detectable fracture aperture. a The resistivity reduction ratio for horizontal fractures, b the maximum variation of azimuthal resistivity for vertical fractures, c the resistivity reduction ratio for 45° fractures, d the maximum variation of azimuthal resistivity for 45° fractures

Full size image

4 HARL response of crossing fractures

A fracture group usually exists in the form of crossing fractures. This article only discusses the situation of two crossing fractures, as shown in Fig. 7, in which the bedrock resistivity is 10,000 Ω m and the fracture aperture is 50 μm. Assuming that one arbitrary dipping angle fracture respectively crosses with one horizontal fracture and one vertical fracture, by comparing their responses (solid lines) with the response of parallel fractures (dotted lines), the apparent resistivity of crossing fractures increases more slowly, as shown in Fig. 7a, c. In comparison, the variation of azimuthal resistivity of crossing fractures that include horizontal fracture is weaker and those that include vertical fracture gradually increase as the dipping angle increases, as shown in Fig. 7b, d.

Fig. 7
figure 7

HARL response of crossing fractures. a High-resolution dual laterolog curves, b deep azimuthal resistivity curves, c high-resolution dual laterolog curves, d deep azimuthal resistivity curves

Full size image

Figure 8a shows a deep azimuthal resistivity imaging of crossing fractures with one horizontal and one 75° high-angle fracture, and Fig. 8b shows a shallow azimuthal resistivity imaging of crossing fractures with one 120° and one 170° fracture, in which the bedrock resistivity is 3000 Ω m, and the fracture aperture is 200 μm. The results show that, in crossing fractures, the apparent resistivity is mainly affected by the low-angle fracture, while the variation of azimuthal resistivity is mainly affected by the high-angle fracture. The combination type of crossing fractures can be clearly displayed.

Fig. 8
figure 8

Azimuthal resistivity imaging of crossing fractures. a Deep azimuthal resistivity imaging of 0° and 75° crossing fractures, b shallow azimuthal resistivity imaging of 120° and 170° crossing fractures

Full size image

5 HARL response of high-angle fracture beside the borehole

Fracture and structure prediction beside the borehole is very important, but it is challenging for conventional logging. The HARL response is utilized to study vertical fractures beside the borehole, and the apparent resistivities are shown in Fig. 9a, c, and e, in which the fracture apertures are 50, 200, and 1000 μm, and the bedrock resistivities are 10,000 and 3000 Ω m, respectively. When the vertical fracture intersects the borehole, which means that the distance from the fracture to the center of borehole is less than 0.1 m, the apparent resistivity is significantly small and a positive separation occurs between the deep and shallow resistivities. As the vertical fracture is gradually far away from the borehole, the positive separation gradually disappears. For the vertical fracture far from the borehole, if the fracture aperture and the resistivity ratio are large enough, negative separation occurs. This is because the impact of deep laterolog is greater than that of the shallow one, resulting in faster decrease of the deep lateral resistivity.

Fig. 9
figure 9

HARL response of vertical fracture with different distances from the center of borehole. a High-resolution dual laterolog curves of a 50 μm fracture, b deep azimuthal resistivity curves of a 50 μm fracture, c high-resolution dual laterolog curves of a 200 μm fracture, d deep azimuthal resistivity curves of a 200 μm fracture, e high-resolution dual laterolog curves of a 1000 μm fracture, f deep azimuthal resistivity curves of a 1000 μm fracture

Full size image

The azimuthal resistivity response is shown in Fig. 9b, d, and f. When the vertical fracture intersects the borehole, the azimuthal electrode closest to the fracture plane has the minimal resistivity, and the variation of azimuthal resistivity is obvious. When the vertical fracture is near the sidewall, the variation is the largest. As the vertical fracture is gradually far away from the borehole, the variation gradually weakens. As the distance between the 1st azimuthal electrode and vertical fracture is the nearest, it has the smallest resistivity, and the 6th electrode has the largest resistivity because of its farthest distance.

For vertical fractures beside the borehole, the farthest detectable distance is determined as the ratio of the maximum variation of deep azimuthal resistivity and the deep lateral resistivity that reaches 10 %. As shown in Fig. 10, when the bedrock resistivity is 3000 Ω m and the fracture apertures are 50, 200, and 1000 μm, the farthest detectable distances are 0.25, 0.40, and 0.7 m, respectively. When the bedrock resistivity is 10,000 Ω m, and the fracture apertures are 50, 200, and 1000 μm, the farthest detectable distances are 0.40, 0.67, and 1.1 m, respectively.

Fig. 10
figure 10

Determination of the farthest detectable distance of a vertical fracture beside the borehole

Full size image

6 Conclusions

A good correlation exists between HARL and fracture aperture. A relatively low apparent resistivity and negative separations between deep and shallow resistivities present for low-angle fractures, while a relatively high azimuthal resistivity and positive separations exist for high-angle fractures.

Azimuthal resistivity imaging can be used to identify the presence of the fractures and their combination type. As the fracture dipping angle, aperture, or the resistivity ratio increases, the variation of azimuthal resistivity increases.

According to the positive or negative separations between the deep and shallow resistivities and the variation of azimuthal resistivity, high-angle fractures surrounding the borehole can be determined when the fracture aperture is relatively large and the resistivity ratio of bedrock and fracture medium is high.