Abstract
For safe and reliable machine operation, maintenance, repair and overhaul (MRO) activities are required. Spare parts demand forecasting and inventory planning, which is an important part of MRO activities, must be accurate to avoid costs because of surplus spare parts or machine downtimes. The restriction of reduced accessibility to wind turbines during the winter months also has to be taken into account when planning maintenance activities and spare part inventories for wind farms. The presented model provides the most economic stock quantity under given environmental conditions. It is based on the proportional hazards model, which is extended to calculate the remaining useful component life time and derive required spare parts inventory levels. The presented model is validated, using condition monitoring data and environmental data of an onshore wind farm. Comparison of the spare part inventory prediction to wind farm’s failure data proves the model’s accuracy. Parameter analyses show that the model can be applied for spare parts inventory planning under consideration of environmental conditions.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Problem statement
Maintenance, repair and overhaul (MRO) activities are necessary to ensure safe and reliable machine operation. For many MRO processes, spare parts are essential, because their non-availability causes machine downtime. It is prolonged in case of long lead times that entail high operation costs. Hence, stock holding is necessary to achieve high service levels, allowing for short machine downtime. In contrast to high service levels and spare parts availability, inventory costs need to be considered to attain economic machine operation. There is a trade-off between service and inventory costs. The point of cost-optimal machine operation has to be determined.
For implementing weather restrictions, utilizing available information and achieving minimum operation and maintenance cost, mechanically stressed wind energy components have been investigated within the research project “EloWind”—service logistics for wind energy turbines. In the proposed method, a Weibull proportional hazards model (PHM) is combined with a Bernoulli approach. The spare demand is forecasted based on wind speeds and operating temperatures. A cost-optimal inventory level of spare parts is derived, taking into account inventory costs of spare parts and downtime costs of wind energy turbines. The proposed method is validated with data of an onshore wind turbine farm.
2 State of the art
2.1 Maintenance costs
Maintenance costs comprise direct and indirect cost. They include all costs incurred during a predefined time range, like operational costs, costs for spare parts, cost for maintenance personnel as well as costs for machine breakdown [1]. In the literature, the total maintenance costs during the lifetime of a unit are referred to as average cost per unit good time [2–4]. Minimizing the average costs per unit good time is, apart from machine availability, the overall aim of maintenance. Equation 1 shows all parts of the total maintenance cost.
c It , total maintenance cost (€); c Is , costs for service providers (€); c Ii , costs for internal maintenances processes (€); c PA , costs for machine downtime (€); c F , costs for secondary damages (€); and c M , costs for additional expenses (€).
Internal maintenance cost include cost for maintenance measures itself, supply of raw material, resources, tools and spare parts as well as depreciation for operative units. Depreciation costs accrue for wearing components operating many periods. They are based on the units’ price and the length of the life cycle. The second cost factor, costs for service providers, complies with the service contract between the service provider and the machine operator. It varies with terms of services, for example if spare parts and repair cost are included, the operator of the machine does not have to realize spare parts planning. If a failed unit destroys other units, secondary damages are the consequence. The fourth cost factor comprises additional expenses, which are common in production, because it is often possible to produce more goods in advance and, herewith, compensate loss of production costs. Costs for secondary damages as well as costs for additional expenses are neglected in the following, because secondary damages arise randomly and additional expenses cannot avert consequences of machine downtime in the field of wind energy. Costs for machine downtime include costs for lost sales or, in case of wind energy business, missing remuneration for feeding electricity into the grid. The costs are determined by the feed-in tariff, the power of the wind turbine, the share of full load hours as well as the duration of the breakdown (Eq. 2).
t d , duration of machine breakdown (days); f, feed-in tariff per kilowatt hour (€/kWh); l j , power of the wind turbine (kW); and p V , share of full load hours per day (%/day).
Maintenance and spare parts stocking strategy mainly influence the maintenance cost structure. This becomes clear when scheduled or unscheduled renewals are considered. For scheduled renewals, maintenance time equals repair time that accords to the minimal maintenance time. If the renewal is unplanned, additional time intervals are added to the repair time. These periods are caused because maintenance cannot be performed. Reasons for non-feasibility are [1]:
-
missing spare parts,
-
inclement weather conditions and
-
other missing maintenance resources, like maintenance personnel.
Inclement weather conditions might be met by maintenance planning and preventive maintenance tasks, and missing spare parts can be avoided by high inventory levels that can lead to high capital costs. Capital costs are calculated as presented in Eq. 3.
c Li , spare part inventory cost per day (€); c ETi , spare part procurement cost (€); z L , inventory rate (%); z E , interest rate (%); and t Li , duration of stocking (days).
The inventory rate accumulates costs for personnel working in the inventory, costs for storage space and administrative costs, which are not directly linked to individual spare parts. If spare parts are expensive and stored for a long time, high stocking costs are incurred. These stocking cost are in conflict with the overall maintenance aim of minimal costs. The resulting trade-off between low inventory costs and short machine downtime is addressed by spare parts and maintenance planning.
2.2 Spare parts planning
Spare parts replace worn and defective units, which are unable to fulfill their proposed function [5]. Systems without redundant units depend on spare parts in case of malfunctions. Predicting the amount of spare parts needed in the future is denoted as spare parts management or spare parts logistic. The field of spare parts logistic is split into the topics data preprocessing, inventory management and demand forecasting.
Data preprocessing is used to delete wrong data sets and to classify spare parts in correspondence to their demand pattern or according to their procurement costs, with the aim of grouping spare parts with similar properties [6]. Herewith, complexity of spare parts planning is reduced and demand prediction algorithms can be utilized according to their optimal field of application.
Inventory management as the second field of spare parts logistic aims at the most economic inventory level and the procurement strategy. Well-known models of multi-echelon inventory systems are the METRIC model by Sherbrooke or the model by Muckstadt [7, 8]. The objective of the current and future research is relaxing the restrictive assumptions of these two approaches. Examples are models taking into account lateral transshipments [9] or models assuming finite repair capacity in case of repairable item systems [10, 11]. Basten et al. and Kennedy et al. provide extensive reviews of latest and past inventory management models [12, 13].
The resulting inventory levels of inventory management models depend on the forecast of demand prediction methods. There are two major groups of demand prediction: quantitative and qualitative methods. Qualitative methods base on expert knowledge. They do not implement historical data. Instead, these methods solely rely on the judgment of experts, which often leads to unsatisfactory prediction results. In the group of quantitative methods, time series, life expectancy and causal analytic approaches are included. The most popular time series analysis methods are [14, 15]:
-
moving average,
-
exponential smoothing,
-
Crostons’ method or
-
regression analysis.
Time series analysis methods are applied if historical demand patterns are expected in the future. The algorithms try to recognize patterns in the demand history and extrapolate them into the future [16–18]. In addition to demand data only, life expectancy models also utilize information about lifetime of failed components and the current age of components. By that, they convey failure functions for the life cycle of component, which are used to predict the probability of failure at a given instance [19]. These models have also been extended to include more parameters, describing the probability of failure as a function of temperature, machine stress or surrounding conditions [20–22]. Heng et al. [23] provide a survey of reliability-based forecasting models.
Time series analysis methods are easy to apply, but do not offer the possibility of considering condition monitoring information, available in nearly every wind turbine. Therefore, advanced methods are used for failure prediction, which allow for consideration of information of log-files and condition monitoring systems.
2.3 Proportional hazards model
The PHM represents a semi-parametric model for analyzing failure data without defining a failure distribution. The PHM has been introduced by Cox in [24] and has since then widely been used in the field of biology. It is capable of integrating and interpreting parameters that describe the load or the operation conditions of components. It is based on parametric or a nonparametric baseline hazard function h 0(t). Influences of covariates z m are quantified by the regression coefficient α m (Eq. 4).
h 0(t), baseline hazard function; h(t; z), modified hazard function; z m , covariates; and α m , regression coefficient.
The major assumption of the model is a constant hazard ration (h 1(t; z) and h 2(t; z)) during lifetime, meaning that a covariate like wind speed has the same influence on the probability of survival at two different instances of time.
When modeling mechanical wear, the unspecific baseline hazard function can be substituted by the Weibull hazard rate. Equation 5 presents the two parametric Weibull hazard rate.
β, shape parameter and T, scale parameter (weeks).
The model is mainly applied in the field of medicine, whereupon it has also been used in the technical domain [25]. Lanza et al. and Abernethy extensively discuss different types of Weibull models for technical applications [19, 26]. Vlok utilizes the PHM in a technical domain and estimated the instant of maintenance [27]. Wang and Ghodrati realized spare parts prediction by means of a stochastic process based on the PHM [28, 29]. In contrast to them, Tracht et al. presented a method to preprocess condition monitoring and operational information and implemented them into an enhanced forecast model [28, 30]. The method proposed in this paper is an advancement of the model presented by Tracht. Demand levels are integrated into an inventory planning approach, but do not allow for integration of wavering surrounding conditions.
3 Approach
The power train of a wind turbine is in the focus of the research project. There are several sensors located in the power train that monitor various condition parameters, for example, wind speed, power output, temperature of mechanical components or operational time. For utilizing this information, the PHM is extended to a Weibull PHM. This parametric model and the cost functions presented are integrated in the framework, shown in Fig. 1. It highlights analysis and computation processes and their interconnection between each other.
The output of the model is the most economic stock quantity under given environmental conditions, like increased wind speeds that will also increase machine breakdown costs. By comparing costs for surplus of stock and stock-out costs, the cost-optimal stock quantity can be calculated.
3.1 System analysis
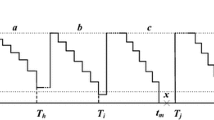
The integrated model is based on a system analysis process. The aim of that first step is an identification of critical components in terms of technical necessity. Crucial components need to be stored or purchased in the instant of a request. Figure 2 presents the functional model of the main components of the power train exemplarily. A functional system is used for fundamental fault analysis of a system and shows the impact of individual functions on availability and reliability [31].
From the functional system in Fig. 2, it can be concluded that availability of every component is crucial to system availability. If there were two redundant components, it would have been possible for the machine to operate, despite malfunction of one component. In the example presented, flawless operation of every component is necessary.
For components in stock, further classification steps will be conducted. They include classification regarding demand pattern, demand level and purchasing costs. Demand pattern can be analyzed by means of plotting historical data. This is necessary because time series analysis approaches have to take into account demand patterns for achieving low prediction errors.
3.2 Demand prediction
When integrating condition monitoring data in a correctly modeled and validated PHM, the result will be a probability of failure at the instant of investigation. In case of mechanical components subject to wear, the semi-parametric PHM can be fully parameterized. Herewith, the PHM becomes a Weibull PHM. Therefore, the probability of failure during lead time for an individual component is calculated (Eq. 6).
Fx(t), failure probability during period x to t, conditional the component is operational at instant x (–); F(t), failure probability at the instant t (–); and F(x), failure probability at the instant x (–).
For spare parts planning, the average failure probability during lead time of all components is integrated into a Bernoulli process. For that reason, the mean failure probability of all components is calculated (Eq. 7). It is inserted into the Bernoulli process that also integrates the number of components monitored.
n, number of components (pieces) and \( \bar{F}x\left( t \right) \), mean failure probability of all components during lead time (–).
Using the Bernoulli process, the probability for 0, 1, 2, m demands during lead time is estimated for a defined number of wind turbines or components in operation. Equation 8 presents the cumulative density function of the Bernoulli process [32].
m, demand level during prognosis horizon (pieces).
Therefore, it is possible to calculate stock out and surplus probability, which can be multiplied with the daily downtime and daily inventor cost, respectively.
3.3 Inventory planning
With the help of Eq. 8, the occurrence probability of a specific demand level is estimated. The calculated probability combined with cost parameter of surplus material and downtime because missing spare parts allow for cost-optimal inventory planning. For investigation purposes, the S − 1/S strategy will be used, whereas every other strategy could also be implemented in the model. The strategy is chosen because stock level for expensive, slow moving spare parts is planned at the instant of demand. The stock level leading to minimal total costs per day is calculated as shown in Eq. 9 [33].
c t , total costs per day (€); m, demand level during lead time (pieces); S, stock level (pieces); p m , probability of appearance (–); c d , downtime cost per day per component (€/piece); and c i, inventory cost per day per component (€/piece).
Stock-out costs arise when inventory level is lower than demand. The first expression in Eq. 9 represents daily downtime cost, caused by missing material. In the second expression, the probability of surplus material is multiplied with the inventory cost per day. Minimizing this function leads to the cost-optimal inventory level, because further cost parameter named in Eq. 1 cannot be influenced by means of increasing or lowering spare parts inventory level.
4 Results
4.1 Validation of demand forecasting
Table 1 shows the data set used for validation of the proposed method. Demand data are clustered by years, in which the requests took place. Because of the low sample size, data are not split into test and validation data. Instead, validation takes place by comparing prognosis results of the proposed method to established and well-tested methods, like the method proposed by Abernethy [19] or exponential smoothing. Rabe et al. [34] propose a similar validation approach.
In Fig. 3, forecast results based on exponential smoothing and discrete demand data are presented.
The figure shows many periods without demand. For that kind of demand pattern, either Croston’s algorithm or exponential smoothing is used to predict demand [35]. There is no linear or seasonal trend in the demand pattern, which points to the simple exponential smoothing method. The parameter estimate α = 0.0001. When forecasting the demand for the following 6 months, this parameter leads to the results presented in Table 2. It presents the point forecast as well as the forecast levels of the confidence intervals of 0.77 and 0.95. The intervals are chosen because they make the comparison with the results of Bernoulli’s approach possible.
One demand is estimated by the point forecast for the following 6 months. For the upper threshold levels of the confidence intervals, two parts are estimated respectively. The forecast results are rounded, because spare parts can only be stored in entire pieces.
In addition to demand data, information about the lifetime is utilized for Weibull parameter calculation. This is realized with the help of the maximum likelihood method, including condition monitoring information. The lifetime is calculated based on days. The values of Weibull parameters for the probabilistic model are presented in Table 3. Investigations of condition monitoring data highlighted the most significant correlation between the parameter temperature of stator 2 and lifetime in this example of wind energy turbines. Tracht et al. [30] showed that the combination of these parameters generated the best result and the lowest p value of the Chi-square test. Contrary to the Arrhenius law, which only takes into account temperature, other parameters can also be used for this model, allowing for a broader application [21].
The investigations were conducted using a Weibull PHM, which comprises a baseline hazard function. The baseline hazard function is determined based on failure probability data. The parameters impacting the hazard function—called covariates—can be the temperatures of the generator, the stator, the main bearing or the nominal power output. The amount of the impact of the covariates on the Weibull PHM is determined by regression parameters, which are calculated, applying the maximum likelihood approach.
The positive regression parameter shows the positive correlation between temperature exceedances and end of life. When utilizing these parameters for demand prediction, the condition information considered in the model also needs to be predicted. In this prediction scenario, the temperature of the stator during time of prognosis is assumed to rise forty times over the threshold of 100 °C. Therefore, the outcome of the Weibull PHM is inserted to formula 6 to calculate the failure probability of every single unit.
As proposed by Abernethy, individual failure probabilities during prognostic time intervals are cumulated and the mean of the failure probability is determined [19]. Therefore, the point estimate for the conventional probabilistic demand prediction method is calculated (probabilistic method). By means of the proposed combined method, it is possible to estimate probabilities of occurrence of a certain demand level. The demand level and its probability of occurrence are used for inventory planning (formula 8). The condition monitoring information is considered in the Weibull PHM. The outcome of its parameter estimation, distribution parameter and regression coefficients of covariates, as shown in Table 3, is inserted into the framework presented in Fig. 1 (combined method WPHM). Demand forecasting results for the three described methods are presented in Table 4.
The results in Table 4 show that the proposed method leads to results comparable to conventional methods. The advantage of the combined method is the integration of information about the lifetime and condition monitoring data and, therefore, compensating missing demand history information. Furthermore, it is possible to determine the probability of occurrence and to assess the financial impact of stock outs and surplus material by considering environmental conditions in spare parts planning.
4.2 Dynamic inventory planning
For validation of the dynamic planning approach, parameter analyses have been conducted. During 1 year, the ratio between the two cost parameter inventory and downtime costs varies because wind speed influences downtime cost, as shown in Eq. 2. Therefore, the parameter η is introduced. It is the ratio between inventory and downtime cost per day (Eq. 10).
K i, inventory cost per day (€); K d, downtime cost per day (€); and η, cost ratio (–).
Varying η and mean failure probability, cost minimal stock level for 20 operating components has been simulated. If η equals 1, stock level rises linearly with increasing average failure probability. Whenever downtime costs are significantly lower than inventory cost (e.g., η = 1/4), stock level should be increased to achieve minimal total cost. With an increasing failure probability, more spare parts should be put in stock. Nominal power output increases with higher wind speeds. For example, average failure probability equals 0.3 and η equals 1/1 during summer time. In winter, downtime costs increase because of higher wind speeds, which lead to η = 1/2. For cost-optimal spare parts provisioning, stock level should be increased by one spare part. The results shown in Fig. 4 highlight the necessity to investigate failure probability and cost parameters, because interdependencies between stock level and minimal total costs are not linear for every scenario.
Forecasting accuracy of the proposed method improves with the amount of available historical data for calculating the remaining useful lifetime. The method is not suitable for parts that only have a short lifetime in relation to the planning period, because the failure rate caused by a parameter (e.g., wind) has to remain constant during the planning period.
5 Summary
The research work conducted within the project EloWind made it possible to utilize information of condition monitoring systems already available and integrate them into a novel probabilistic planning approach. The planning approach has been evaluated and tested for slow moving, expensive spare parts of a power train. Above that, wavering surrounding conditions in terms of different wind speeds are considered in the developed model. It is the first model to allow for consideration of environmental conditions. Interdependencies between all relevant parameters are presented by means of parameter studies. Thereby, stock levels can be dynamically adjusted regarding the time of the year and lowering maintenance costs. This will reduce energy costs generated from wind turbines and will make renewable energy resources more competitive. The presented model is a first example of integrating surrounding conditions into a probabilistic planning approach. The example calculation shows very promising results. Further case studies and extensive laboratory experiments to analyze the impact of additional parameters will be conducted in the future.
References
Tracht P, Schuh J, Maier K (2012) Stochastische Einflüsse auf die Instandhaltung von Windenergieanalagen. Zeitschrift für wirtschaftlichen Fabrikbetrieb 1–2:99–103
Warnecke M (2008) Optimierung der Instandhaltungsplanung mit genetischen Algorithmen unter Berücksichtigung des Speicherverhaltens bei der Verfügbarkeitsprognose von Kraftwerksanlagen. Dissertation, Technische Universität Cottbus, Fakultät für Maschinenbau, Elektrotechnik und Wirtschaftsingenieurwesen
Jorgenson DW, McCall JJ, Radner R (1967) Optimal replacement policy. In: Theil H (ed) Studies in mathematical and managerial economics, vol 8. Amsterdam, North-Holland Publishing, XII
Zhao X, Bordes L, Fouladirad M, Bèrenguer C (2010) Condition-based inspection/replacement policies for non-monotone deteriorating systems with environmental covariates. Reliab Eng Syst Saf 95:921–934
VDI 3423 Ersatzteillisten (1976) Allgemeines. Beuth Verlag GmbH
Recknagel S (2008) Optimierung der Langzeitprognose für den Allzeitbedarf von Ersatzteilen durch materialklassenspezifische Bedarfsplanung. Dissertation, Otto-von-Guericke-Universität Magdeburg
Sherbrooke C (2004) Optimal inventory modeling of systems. Kluwer Academic Publishers Group, Boston
Muckstadt J, Mikosch S, Robinson S, Resnick (2005) Analysis and algorithms for service parts supply chains. Springer, New York
Paterson C, Kiesmüller G, Teunter R, Glazebrook K (2011) Inventory models with lateral transshipments: a review. Eur J Oper Res 210:125–136
Selcuk B (2013) An adaptive base stock policy for repairable item inventory control. Int J Prod Econ 143:304–315
Kim JS, Kim TY, Hur S (2007) An algorithm for repairable item inventory system with depot spares and general repair time distribution. Appl Math Model 31:795–804
Basten R, van Houtum G (2014) System-oriented inventory models for spare parts. Surv Oper Res Manag Sci 19:34–55
Kennedy WJ, Patterson J, Fredendal L (2002) An overview of recent literature on spare parts inventories. Int J Prod Econ 76:201–215
Silver EA, Pyke DF, Peterson R (1998) Inventory management and production planning and scheduling. Wiley, New York
Hopp WJ, Spearman ML (2001) Factory physics. McGraw-Hill, Boston
Croston JD (1972) Forecasting and stock control for intermittent demands. Oper Res Q 23:289–303
Makridakis S, Wheelwright S (1978) Forecasting: methods and applications: the Wiley/Hamilton series in management and administration. Wiley, Santa Barbara
Teunter R, Duncan L (2009) Forecasting intermittent demand: a comparative study. J Oper Res Soc 60:321–329
Abernethy RB (2006) The New Weibull Handbook. Robert B. Abernethy Publishing, North Palm Beach, FL
Loukmidis G, Luczak H (2001) Lebensorientierte Planungsstrategien für den Ersatzteilbedarf. In: Barkawi SK, Baader A, Montanus (eds) Erfolgreich mit After Sales Service: Geschäftsstrategien für Servicemanagement und Ersatzteillogistik, Springer, Heidelberg, pp. 251–270
Nelson W (1990) Accelerated testing: statistical models, test plans and data analyses. Wiley, New York
Ebeling C (1997) Introduction to reliability and maintainability engineering. McGraw-Hill, New York
Heng A, Zhang S, Tan A, Mathew J (2009) Rotating machinery prognostics: state of the art, challenges and opportunities. Mech Syst Signal Process 23:724–739
Cox DR (1972) Regression models and life-tables. J R Stat Soc 34:187–220
Eulenburg CH (2009) Überleben, Progredienz und Tod: Multistate-Modelle zur Analyse konkurrierender und nachzeitiger Ereignisse. Disseration, Universität Hamburg
Lanza G, Niggeschmidt S, Werner P (2009) Optimization of preventive maintenance and spare parts provision for machine tools based on variable operational conditions. CIRP Ann Manuf Technol 58:429–432
Vlok VPJ, Coetzee JL, Banjevic D, Jardine AKS, Makis V (2002) Optimal component replacement decisions using vibration monitoring and the proportional-hazards model. J Oper Res Soc 53:193–202
Ghordrati B (2005) Reliability and operational environment based spare parts planning. Lulea University of Technology, Lulea
Wang W (2007) A prognosis model for wear prediction based on oil-based monitoring. J Oper Res Soc 58:887–893
Tracht K, Goch G, Schuh P, Westerkamp JF, Sorg M (2013) Failure probability prediction based on condition monitoring data of wind energy systems for spare parts supply. CIRP Ann Manuf Technol 62:127–130
VDI 2888 (1999) Maintenance condition monitoring. Verein Deutscher Ingenieure. Beuth, Berlin
Dietrich E (2009) Statistische Verfahren zur Maschinen- und Prozessqualifikation. Hanser, München
Thonemann U (2010) Operations management: Konzepte, Methoden und Anwendungen. 2 edn. Pearson Studium
Rabe SM, Spieckermann S, Wenzel S (2008) Verifikation und Validierung für die Simulation in Produktion und Logistik: Vorgehensmodelle und Techniken, VDI-Buch. Springer, Berlin
Willemain TR, Smart CN, Schwarz HF (2004) A new approach to forecasting intermittent demand for service parts inventories. Int J Forecast 20:375–387
Author information
Authors and Affiliations
Corresponding author
Additional information
This article is part of a focus collection on “Logistics in the Networked Industry” based on the BVL’s 7th International Scientific Symposium on Logistics in Cologne in 2014.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Schuh, P., Schneider, D., Funke, L. et al. Cost-optimal spare parts inventory planning for wind energy systems. Logist. Res. 8, 4 (2015). https://doi.org/10.1007/s12159-015-0122-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s12159-015-0122-7