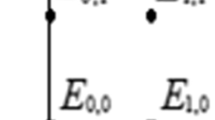Introduction

The ionosphere of the Earth is a partly ionized gas that surrounds the planet from about 50 km up to 1000 km and above. Its formation is due to the photoionization by the Sun’s ultraviolet light, for which it exhibits a diurnal variation, with a maximum of ionization around local noon. Superimposed to the regular diurnal variation, the ionosphere may exhibit disturbances, due to various phenomena originating on the Sun (e.g. Coronal Mass Ejection (CME)) and that propagating through the magnetosphere-ionosphere system (Mendillo, 2006), contribute to the so called Space Weather. As an example, (Fagundes et al., 2016), studied the response of the ionosphere (F region) in the Brazilian sector during the extreme space weather event of 17 March 2015 using a large network of 102 Global Positioning System (GPS) stations. They observed that the vertical total electron content (vTEC) was severely disturbed during storm and recovery phases. Under the storm phase, a positive ionospheric effect was seen, followed by a negative effect during the recovery phase.

vTEC is among the ionospheric parameters worldwide used to analyze the state of the ionosphere, with the aim to forecast its variability being the ionosphere the largest contributor to the error budget for the Global Navigation Satellite Systems (GNSS) positioning applications. vTEC is a projected slant TEC (sTEC, i.e. the integration over the path between satellite radio transmitter and the ground-based receiver) onto a perpendicular path after a proper calibration of sTEC (see, (Cesaroni et al., 2015)) and the application of a mapping function under the assumption that the ionosphere is a thin layer (Mannucci et al., 1993).

Several machine learning models have been developed for vTEC forecasting. These machine learning models have been mostly trained using traditional loss functions such as the Mean Squared Error (MSE) and Mean Absolute Error (MAE). For instance, Xia et al. (2022) employed the MAE metric to construct a novel encoder-decoder structure incorporating a convolutional layer within a short-term memory (ED-ConvLSTM) network for the purpose of predicting vTEC on the global scale. The utilisation of MSE as a foundational metric for constructing an innovative vTEC model was considered in the studies conducted by Cesaroni et al. (2020) and Shenvi et al. (2023) respectively.

In order to predict the size of the ionospheric anomalies, the authors of Liu et al. (2021) created a loss function that was incorporated into an image-based machine learning model. The forecasting accuracy was analyzed for a lead time of 10-60 minutes. The machine learning algorithm used the so-called \(convLSTM-L_{c}\) and the authors showed that \(convLSTM-L_{c}\) outperforms other models including \(convLSTM-L_{1}\), \(convLSTM-L_{2}\) and the persistence model significantly. The \(convLSTM-L_{c}\) implementation is a purely ground-based GNSS data-driven approach without inputs from the solar-geomagnetic drivers.

The use of a deep recurrent neural network with Long-Short Time Memory (LSTM) and the root mean square error (RMSE) as the loss function has been demonstrated in Zewdie et al. (2021) for the purpose of data-driven vTEC forecasting. The researchers employed the Random Forest algorithm to conduct regression analysis and assess the statistical significance of the input variables. The LSTM technique was utilised to predict the vTEC up to a horizon of 5 hours. During the process of hyper-parameter selection, the researchers saw that RMSE did not exhibit a substantial drop after 200 epochs. Consequently, they determined that setting the number of training epochs to 200 would be appropriate. An accurate prediction was obtained with a low RMSE, but this exhibits an upward trend as attempts are made to forecast at greater temporal distances.

The Huber loss function (Huber, 1992), which is not as often used as alternative loss functions, was selected in Wang et al. (2022) for the purpose of conducting statistically robust regression. The researchers developed a predictive model for vTEC on the global scale using a combination of convolutional long short-term memory and spatiotemporal memory. This model aims to forecast the spatiotemporal behaviour of vTEC globally by capturing its temporal variations and spatial characteristics. Additionally, the model incorporates the Huber loss function to mitigate the impact of outliers and noise in the vTEC data, thereby enhancing the accuracy of the vTEC forecasts on a global scale. As much as the performance demonstrated using Huber loss function is promising, this loss function does not take into account the physics constraints on the ionospheric changes.

This study is focused on a single station GNSS receiver location. We introduce novel loss functions for training neural networks for vTEC forecasting from 1 to 24 hours in advance. A major contribution of this work is the design, for the first time, of physics-informed loss functions which include constraints imposed on the MSE built-in function. The rest of this paper is organized as follows. In section II, we discuss the data used and present the physics-informed loss functions designed. In Section III we provide and discuss extensive experimental results. Finally, in Section IV we draw our conclusions and highlight further possible investigations.

Data and methods

Data

The GNSS data is acquired from the Archive of Space Geodesy maintained by National Aeronautics and Space Administration (NASA), which may be accessed at the following URL: (https://cddis.nasa.gov/archive/gnss/data/daily). Specifically, we deal with 30-second GNSS data obtained from regional data collecting centres of the International GNSS Service (IGS). These data are compressed using the Receiver Independent Exchange (RINEX) format and thereafter transmitted to the Crustal Dynamics Data Information System (CDDIS) on a daily basis. To extract vTEC of mid-latitude station Tsukuba (36.06\(^{o}\) N, 140.05\(^{o}\) E) from the RINEX file format, we made use of the calibration algorithm developed by Ciraolo et al. (2007) and detailed in Cesaroni et al. (2015, 2021). This algorithm is able to estimate sTEC at each Ionospheric Pierce Point (IPP) by computing the Differential Code Biases (DCBs) for each arc of observation. The assumption for this estimation is that the ionosphere can be considered as a thin layer at an altitude of 350 km so that the sTEC can be projected to the vTEC by applying a geometric mapping function. The vTEC spatial beavhiour is described by a polynomial function of the Modified Dip Latitude (MODIP) and Local Time that is also used to compute the vTEC over the GNSS station.

Our estimated vTEC dataset includes 2880 values per day, so we down-sample them considering 5-minute intervals by averaging 10 points at a time and centering them. To fix the vTEC missing values, we use the linear interpolation when the missing gap is of few hours as maximum. Within a hour, the forward interpolation is applied. For more than one hour up to four hours, both forward and backward interpolations are applied. For longer periods, we use the median values evaluated on the previous 27 days.

The full set of external drivers used at the beginning of the study are listed in Table 1, by separating them in three groups. Missing values have been fixed using interpolation and constant padding. Before selecting the two most important external drivers in correspondence to forecasting horizons (through the application of permutation of feature importance technique), we search for their linear correlation. So we compute the Pearson correlation coefficient (\(-1\le \rho \le 1\)) among drivers and select \(\rho = 0.5\) as a moderate threshold. Then, we exclude those external drivers for which \(|\rho | \ge 0.5\). However, the exclusion process shall guarantee that the three groups of indices have at least one index in the remaining set of them. In the end, this process allows to reduce both the number of external drivers available and the influence of multicollinearity in getting a reliable interpretation in terms of its statistical significance. This also facilitate the permutation of feature importance technique in selecting the couple of external drivers to be used in the Artificial Neural Network (ANN).

Table 1 The external drivers used in this study are from the year 2006 to 2018, downloaded from https://cdaweb.gsfc.nasa.gov
Full size table

We want to retain at least one index from each group shown in Table 1. To this end, taking into account Fig. 1, we discard all of the indices whose removal makes the remaining indices uncorrelated. Therefore, for the Auroral Electrojet group we retain AE, for the Geomagnetic group we retain SYM-H and, finally, for the Magnetic and Solar group we retain the following indices: F10.7, proton density, solar wind (Proton QI), the magnitude of the interplanetary magnetic field B (nT), the vector components (Bx, By, Bz) and the velocity (Vx, Vy , Vz).

Fig. 1
figure 1

Pearson correlation coefficient among the indices

Full size image
Fig. 2
figure 2

The dynamics of feature importance of the external drivers at different forecasting horizons

Full size image

In order to ascertain the most influential external drivers, the permutation technique is employed, which is a feature importance algorithm. This algorithm is applied to the remaining set of external drivers. The analysis incorporates eleven different machine learning models, namely AdaBoost (AB), Decision Tree (DT), K-Nearest Neighbours (KNN), Lasso, Linear Regression (LR), Random Forest (RF), XGBoost (XGB), Gradient Boost (GB), Extra Tree (XT), Bagging (with Support Vector Regression (SVR) as the estimator), and Voting (with estimators including AB, DT, KNN, Lasso, LR, SVR, RF, XGB, GB, XT, Bagging, and Voting) (Theodoridis, 2015). The “no free launch theorem” (Wolpert and Macready, 1997) asserts that the performance of several optimisation techniques, namely machine learning models in this context, is similar when averaged across all potential challenges, such as different forecasting horizons. The average importance score is calculated for all forecasting horizons, and Fig. 2 illustrates the variations in the dynamics of the external drivers across different forecasting horizons. The permutation of feature importance algorithm (Altmann et al., 2010) is utilised in order to choose the two most significant external drivers for each forecasting horizons. We limit to two external drivers because increasing the number of them causes an increment in the trainable parameter size of the neural network model which can lead to overfitting and affects the training time.

Fig. 3
figure 3

Architecture of the ANN model. In this architecture we exploit multiple networks whose outputs are then fused together

Full size image

In Fig. 2, it is observed that for all the forecasting horizons, F10.7 (red dots) ranked first with the highest average score of importance. \(B_T\) (blue dots) is the second important external driver for 1 hour and 24 hour forecasting horizons. For the interval 2-23 hours of forecasting horizons, the second best external driver is AE (green dots). These external drivers, together with their respective units, are presented in Table 2 and they include:

  • Solar Flux F10.7: this index has the highest ranking across all predicted horizons. vTEC tends to exhibit a decrease during periods characterized by low solar activity, whereas it shows an increase during periods of high solar activity (Mukesh et al., 2020; Shenvi et al., 2023). Solar activity has a direct impact on the ionosphere, thereby influencing vTEC. The F10.7 solar flux is a frequently employed metric for quantifying solar activity. It has a strong correlation with sunspot counts and serves as an indicator for Ultraviolet (UV) and visible solar radiation levels. Consequently, the utilization of F10.7 is justified due to its established reliability as an indicator of solar activity magnitudes.

  • Magnitude (\(B_T\)) of the Interplanetary Magnetic Field’s (IMF): this is shown to be the second most influential factor for forecasting horizons at 1 and 24 hours. \(B_T\) represents the overall intensity of the IMF. The metric encompasses the amalgamation of magnetic field intensity in the north-south, east-west, and inward-facing solar vs outward-facing solar orientations.

  • Auroral Electrojet (AE): it exhibits a consistent ranking as the second most reliable indicator for predicting horizons ranging from 2 to 23 hours. The purpose of AE is to offer a comprehensive, numerical assessment of magnetic activity within the auroral zone, which is generated by intensified ionospheric currents occurring both below and within the auroral oval. Ideally, the concept refers to the comprehensive extent of variation at a given moment in time from the baseline values of the horizontal magnetic field (h) in the vicinity of the auroral oval.

Table 2 Space weather indices used together with vTEC as an input for the ANN model
Full size table
Table 3 Additional hyperparameters for the ANN model
Full size table
Table 4 This describe the hyperparameters in relation to the number of layers, the activation function, the input size with N being the sample size and the units used in building the ANN model
Full size table
Fig. 4
figure 4

Sliding window algorithm showing the preparation of an input data for an hour forecast horizon. This algorithm is applied to the vTEC and external drivers sequences

Full size image

Machine learning architecture

Neural networks, first described by McCulloch and Pitts (1943), are computational models composed of interconnected neurons arranged in layers. The process of acquiring knowledge and skills involves the modification of synaptic weights in order to minimise a predetermined cost function. The back-propagation technique is considered a significant advancement in the field of neural networks due to its ability to facilitate the training process using a collection of input-output training samples, despite the computational intensity associated with training (LeCun et al., 1989; Rosenblatt, 1958; Theodoridis, 2015). The suggested artificial neural network (ANN) design is depicted in Fig. 3., while Table 3 and Table 4 present more details regarding this architecture. The network consists of four input layers, three of which are structured to accommodate the variables vTEC and the two chosen external drivers (EXT1 and EXT2), the other input layer accommodates the constraint parameters. The input layers containing the vTEC and external drivers chosen are linked to separate dense layers, each having the same number of layers, unit size, and activation function, as indicated in Table 4. The three dense layers are subsequently concatenated and connected to another dense layer, along with the output layer. The input layer containing the constraint parameter is passed to the loss function as inputs for the physics-informed loss function designed.

The sliding window approach is employed to create the input for the ANN model, as seen in Fig. 4, in accordance with the chosen forecasting horizon. The same approach is used for the two selected external drivers. Specifically, the input size is denoted as \(w = 288\), which corresponds to a complete day of data collected at 5-minute intervals. The dataset employed in this study has been standardised using Z-score normalisation. The computation of this is performed as

$$\begin{aligned} z = (x - \mu ) / \sigma , \end{aligned}$$
(1)

where x represents a dataset, while \(\mu \) and \(\sigma \) represents its mean and standard deviation. We do this to center and scale the dataset, since some of the external parameters have different scales.

The input dataset consists of vTEC, the two external drivers chosen and, finally, the constraints parameters. The dataset is divided into three separate datasets (i.e., training, validation, and testing). The sizes of these datasets are 70%, 20%, and 10%, respectively, as seen in Fig. 5.

Fig. 5
figure 5

The vTEC data for Tsukuba station spanning from the year 2006 to 2018

Full size image

In brief, Fig. 6 describes the flow chart of the machine learning algorithm. To begin with, data is prepared for the neural network model, and this include vTEC and the best two external drivers selected during the feature ranking phase using the sliding window algorithm. These external drivers are F10.7 and \(B_T\) for 1 hour and 24 hour forecasting horizons, F10.7 and AE for forecasting horizons in the interval 2-23 hour. Constraint data are similarly prepared using the sliding window. This data is used as constraints in order to defined our physics informed loss function. Next, the ANN is designed, trainable parameters are initialized, the activation function is selected for each layers, hyper-parameters are set, an optimizer to be used is selected for the back-propagation step, and finally the metric for evaluating the models goodness of fitting is defined. This is where the physics-informed loss function comes into play and the constraint data are used. After this development, the ANN is trained, validated and tested.

Fig. 6
figure 6

Flow chart of the machine learning algorithm

Full size image

Loss functions

The loss function helps to measure the “goodness of fit” of a model. In a machine learning algorithm, the trainable parameters are updated in the process of training the model, which is an optimization problem whose objective function is the loss function, to be minimized. The introduction of the back-propagation technique brought a significant achievement to the neural network training process there by solving the optimization problem of minimizing the loss function. Several physics-informed loss functions have been introduced in several other fields in Space Weather. In the field of vTEC forecasting, almost all the neural network models designed uses the traditional loss functions such as mean squared error (MSE), root mean squared error (RMSE), mean absolute error (MAE). In this work, we focus on MSE, which seeks to penalise outliers and forces small errors close to zero. We design five different loss functions by imposing physics-informed constraints in order to improve the performance significantly and also capture strong disturbances. Several external indices were used as constraints imposed on the MSE (Table 5). It is worth noting that, this second set of external drivers are used as constraints aiding to improve the learning process of and therefore the performance of the ANN model, but they are not included in the prediction phase. These external drivers are:

  • Disturbance Storm Time (Dst) index: It gives information about the strength of the ring current around the Earth caused by solar protons and electrons. This helps to quantify the variations of the horizontal component of the geomagnetic field. During quiet days Dst ranges from 0 to -50 nT (Yurchyshyn et al., 2004; Atıcı et al., 2020; Shenvi et al., 2023);

  • Solar wind speed (v): this is the speed of gas from the Sun, and it carries ions and free electrons into the ionosphere (Yurchyshyn et al., 2004; Ren et al., 2020; Shenvi et al., 2023);

  • IMF By: It is the component of the IMF which is oriented perpendicular to the Bx component and to the plane of the Earth’s magnetic equator. IMF By can influence the morphology of the convection cells at high latitude;

  • IMF Bz: This component of the IMF is oriented parallel to the earth’s magnetic axis and during periods of southward (negative) Bz, the solar wind can penetrate deeper into the Earth’s magnetosphere, leading to injection of energy into the magnetosphere-ionosphere system;

  • IMF \(B_{T}\): already described above in “Data”.

Table 5 Indices used as constraints on the loss functions
Full size table

Derivation of physics-informed loss functions

Let \(J(\theta )\) denote the loss function without physics-based constraints imposed on it where \(\theta \) is the trainable parameter. Using MSE as the basic loss function, \(J(\theta )\) is defined as

$$\begin{aligned} J(\theta ) = \frac{1}{N} \sum _{i=1}^{N}{(y_{i} - \hat{y}_{i})^{2}}, \end{aligned}$$
(2)

where N is the number of training samples, \(y_i\) is the actual i-th output and \(\hat{y_i}\) is the corresponding i-th predicted output. Let MSE_v0 represent Eq. 2, and we denote by MSE_v1, MSE_v2, MSE_v3, MSE_v4, and MSE_v5, respectively, the loss functions derived as follows:

Loss function MSE_v1

In this case, we make use of the external indices for determining stormy and quiet events. The indices used here are Dst and Bz. The mathematical formulation of the loss function with constraints imposed on it is given as

$$\begin{aligned} L(\theta , \lambda _{i1}, \lambda _{i2}) ={} & {} \frac{1}{N} \sum _{i=1}^{N}{(y_{i} - \hat{y}_{i})^2} - \nonumber \\{} & {} - \frac{1}{N} \sum _{i=1}^{N}{\lambda _{i1} \sum _{t=1}^{w=288}{x_{it} \odot f_{it}^{Dst}}} - \nonumber \\{} & {} - \frac{1}{N} \sum _{i=1}^{N}{\lambda _{i2}\sum _{t=1}^{w=288}{x_{it} \odot f_{it}^{Bz}}} \end{aligned}$$
(3)

where \(\lambda _{ij} \ge 0\) (lagrangian multipliers), N denotes the number of training instances, t represents the time, the \(\odot \) operator represents element-wise multiplication and \(x_{it}\) is an indicator function defined by Eq. 4, \(f_{it}^{Dst}\) represents the Dst index at instance i and time t and \(f_{it}^{Bz}\) denotes the Bz index at instance i and time t.

$$\begin{aligned} x_{it} = {\left\{ \begin{array}{ll} 1, &{} f_{it} \le {\left\{ \begin{array}{ll} \alpha = -50 \text { nT} &{} \text {for Dst} \\ \beta = -5 \text { nT} &{} \text {for Bz} \end{array}\right. } \\ 0, &{} otherwise \end{array}\right. } \end{aligned}$$
(4)

This loss function seeks to help the learning process of the neural network focus more on stormy events by penalising such instances. In order to achieve this, constraints are imposed on the built-in loss function using the Dst and Bz indices to detect quiet and stormy events. For quiet events, we turn off the penalization property on the loss function; hence, we use the built-in mean square loss function for quiet events.

Loss function MSE_v2

In this case, we utilise the information for the derivative of Bz, which is the north-south component of the IMF. When Bz turns negative, it means that the IMF and the geomagnetic field reconnect with each other, and the particles and energy are free to enter from the solar wind into the magnetosphere-ionosphere system. This is why geomagnetic and ionospheric storms are expected when the Bz flips from northward (positive) to southward (negative). The derivative is computed for an hour-long time interval. The loss function is defined as

$$\begin{aligned} \begin{aligned}&L(\theta , \lambda _{i1}, \lambda _{i2}) = \frac{1}{N} \sum _{i=1}^{N}{(y_{i} - \hat{y}_{i})^2} - \\&- {\left\{ \begin{array}{ll} \frac{1}{N} \sum _{i=1}^{N}{\lambda _{i1} \sum _{t=1}^{w=288}{x_{it} \odot f_{it}^{Dst}}} + \\ + \frac{1}{N} \sum _{i=1}^{N}{\lambda _{i2}\sum _{t=1}^{w=288}{x_{it} \odot f_{it}^{Bz}}} &{} \frac{dBz}{dt} < 0 \\ 0 &{} \text {otherwise} \end{array}\right. } \end{aligned} \end{aligned}$$
(5)

where \(x_{it}\) is defined in Eq. 4. The idea for this loss function also seeks to focus on quiet and stormy events during the learning processes of the neural network by combining the built-in MSE loss function and the penalised MSE loss function defined in Eq. 3 using the sign of the derivative Bz. This kind of combination is inspired by the Huber loss function, which combines L1 and L2 loss functions based on the magnitude of the error. In the case of the Huber loss function, the condition is based on the magnitude of the error, while in this physics-informed loss function, the condition is based on the sign of the derivative of the Bz index in an hour interval.

Loss function MSE_v3

In this case, we make use of the coupling function, including the external indices v, By, Bz, and \(B_{T}\) (Akasofu, 1996; Koskinen and Tanskanen, 2002; Rogers et al., 2016; Wood and Pryse, 2010). Coupling functions are mathematical combinations of measured variables observed in the solar wind just before it impacts near-Earth space. They are used to predict the effect that the solar wind will have (or, for retrospective studies, will have had) on the space-weather environment of the Earth (Lockwood and McWilliams, 2021). The coupling function used is defined as

$$\begin{aligned} \epsilon =&vB_{T}^{\frac{1}{2}} \displaystyle \sin ^{2}{\left( \frac{\theta _{c}}{2}\right) } \end{aligned}$$
(6)
$$\begin{aligned} \theta _{c} =&\arctan {\left( \frac{|By|}{Bz}\right) } \end{aligned}$$
(7)

where \(\theta _{c}\) represents the clock angle which shows relative importance of the y and z components of the IMF and \(\epsilon \) is the quantitative value given by the coupling function.

The loss function is then defined as

$$\begin{aligned} \begin{aligned} L(\theta , \lambda _{i1})&= \frac{1}{N} \left[ \sum _{i=1}^{N} (y_{i} - \hat{y}_{i})^2 \right] + \\&+ \frac{1}{N} \left[ \sum _{i=1}^{N} \lambda _{i1} \sum _{t=1}^{w=288} \epsilon _{it} \right] \end{aligned} \end{aligned}$$
(8)

Using the coupling function as a term in penalising the classical squared loss function helps to include the predicted impacts on the near-Earth space. In order to achieve this, the coupling function is used as a constraint at each instance of the input dataset, for which the Lagrangian dual function in this case is defined by Eq. 8.

Loss function MSE_v4

The loss function is defined as

$$\begin{aligned} \begin{aligned} L(\theta , \lambda _{i1}, \lambda _{i2}, \lambda _{i3})&= \frac{1}{N} \sum _{i=1}^{N}{(y_{i} - \hat{y}_{i})^2} + \\&+ \frac{1}{N} \sum _{i=1}^{N}{\lambda _{i3} \sum _{t=1}^{w=288}{\epsilon _{it}}} - \\&- \frac{1}{N} \sum _{i=1}^{N}{\lambda _{i2}\sum _{t=1}^{w=288}{x_{it} \odot f_{it}^{Bz}}} - \\&- \frac{1}{N} \sum _{i=1}^{N}{\lambda _{i1} \sum _{t=1}^{w=288}{x_{it} \odot f_{it}^{Dst}}} \end{aligned} \end{aligned}$$
(9)

This loss is also developed in order to improve the learning processes of the neural network by combining the constraints introduced in “Loss function MSE_v1” and “Loss function MSE_v3”. These constraints are combined in order to capture all kinds of events. This is because Dst for instance, is not sufficient to define all geospace storms (Borovsky and Shprits, 2017).

Loss function MSE_v5

The last loss function designed is defined as

$$\begin{aligned} \begin{aligned}&L(\theta , \lambda _{i1}, \lambda _{i2}, \lambda _{i3}) = \frac{1}{N} \left[ \sum _{i=1}^{N}{(y_{i} - \hat{y}_{i})^2} \right] - \\&- {\left\{ \begin{array}{ll} \begin{aligned} &{} \frac{1}{N} \sum _{i=1}^{N}{\lambda _{i1} \sum _{t=1}^{w=288}{x_{it} \odot f_{it}^{Dst}}} + \\ &{} + \frac{1}{N} \sum _{i=1}^{N}{\lambda _{i2}\sum _{t=1}^{w=288}{x_{it} \odot f_{it}^{Bz}}} \end{aligned}, &{} \frac{dBz}{dt} < 0 \\ \\ - \frac{1}{N} \sum _{i=1}^{N}{\lambda _{i3} \sum _{t=1}^{w=288} {\epsilon _{it}}}, &{} otherwise \end{array}\right. } \end{aligned} \end{aligned}$$
(10)

where \(x_{it}\) is defined in Eq. 4. This is a conditional combination of loss functions defined in “Loss function MSE_v1” and “Loss function MSE_v3” on the basis of the sign of the derivative of Bz. The change considered is within an hour.

Evaluation metrics

To measure the performance of the loss functions designed for the ANN, we make use of the coefficient of determination \((R^2)\) (Chicco et al., 2021) and the error distribution comparing the built-in MSE to the physics-informed loss functions using the standard deviation (SD) on the training, validation, and test datasets. The evaluation metric \(R^2\) is defined as

$$\begin{aligned} R^{2} = 1 - \frac{SS_{res}}{SS_{tot}}, \end{aligned}$$
(11)

where \(SS_{res}\) and \(SS_{tot}\) represent the residual sum of squares and the total sum of squares respectively. These are defined as

$$\begin{aligned} SS_{res} =&\sum _{i}{(y_{i} - \hat{y}_{i})^2}=\sum _{i}{e_{i}^{2}}\end{aligned}$$
(12)
$$\begin{aligned} SS_{tot} =&\sum _{i}{(y_{i} - \bar{y})^2}, \end{aligned}$$
(13)

where \(y_i\) and \(\hat{y_i}\) are the actual and predicted values for the i-th sample respectively. The mean of y i.e., \(\bar{y}\) is defined as

$$\begin{aligned} \bar{y} = \frac{1}{N}\sum _{i}^{N}{y_{i}} \end{aligned}$$
(14)

.

The evaluation metric SD is defined as

$$\begin{aligned} SD = \sqrt{\frac{1}{N-1}\sum _{i=1}^{N}{({e}_{i} - \bar{e})^2}} \end{aligned}$$
(15)

where N is the total number of observations, \(e_{i}\) is the observation error and \(\bar{e}\) is the mean error which is defined as

$$\begin{aligned} \bar{e} = \frac{1}{N}\sum _{i=1}^{N}{(y_{i} - \hat{y}_{i})} \end{aligned}$$
(16)
Table 6 Evaluation of our proposed ANN architecture on the training dataset using different loss functions
Full size table

The Wilcoxon nonparametric signed ranked test (Conover, 1999) is used to further assess if training the neural network with the physics-informed loss functions actually provides a statistically significant improvement. To conduct the test, it is necessary to establish the null hypothesis (i.e., \(H_0: \mu _D = 0\)), indicating that there is no statistically significant difference in the performance of ANN models using two distinct loss functions across forecasting horizons ranging from 1 to 24 hours. Additionally, the hypothesis (\(H_{A}: \mu _D \ne 0\)) is defined for searching a statistically significant difference in the performance of ANN models using the aforementioned loss functions across the specified forecasting horizons. Furthermore, the significance level associated with the null hypothesis is determined. For sample sizes that are less of, namely 30 or fewer, the statistic test T is calculated and then compared to the critical value obtained from the Wilcoxon signed rank test table. The calculation of T for small samples is computed as

$$\begin{aligned} T = \text {smaller of } \sum {R_{+}} \text { and } \sum {R_{-}} \end{aligned}$$
(17)

where \(\sum {R_{+}}\) is the sum of ranks with positive differences and \(\sum {R_{-}}\) is the sum of ranks with negative differences.

Results

A total of six ANN models were trained, verified, and tested at Tsukuba (36.06\(^o\) N, 140.05\(^o\) E) receiver station, each of them using a distinct loss function: MSE_v0, MSE_v1, MSE_v2, MSE_v3, MSE_v4, and MSE_v5, specified in Eqs. 2, 3, 5, 8, 9 and 10, respectively. When examining the dispersion of the ANN models on the training and validation datasets for various forecasting horizons, it is evident from Table 6 and 7 that MSE_v1 exhibits the highest number of minimum SD, improving the performance of the corresponding ANN model. The average spread of MSE_v1 results to be the lower one on both the training and validation datasets, with mean values of 0.256 and 0.3183, respectively. The performance of the ANN model by using the other loss functions slightly decreases on both training and validation data set. In the former case, the mean values of the spread for MSE_v2, MSE_v0, MSE_v4, MSE_v3, and MSE_v5 are 0.2580, 0.2593, 0.2605, 0.2606, and 0.2624, respectively. In the case of validation data set, the average order of minimal dispersions is as follows: MSE_v3 (0.3191), MSE_v4 (0.3191), MSE_v5 (0.3194), MSE_v0 (0.3197), and MSE_v2 (0.3201).

Table 7 Evaluation of our proposed ANN architecture on the validation dataset using different loss functions
Full size table
Fig. 7
figure 7

Performance measure using coefficient of determination on the test dataset across all forecast horizons

Full size image

Finally, the forecasting performance of the ANN models with different loss functions has been investigated by applying the models to the testing data (Fig. 5) and ranking the performances as function of \(R^2\). As shown in Fig. 7, the model trained and validated with MSE_v1 performs slightly better in terms of \(R^2\) on most of the forecasting horizons. MSE_v1 shows an average \(R^2=0.810\), followed by MSE_v2, MSE_v3, MSE_v4, and MSE_v5 with \(R^2 = 0.808\) each, while MSE_v0 has the worst average \(R^2 = 0.807\).

The error distributions of the six ANN models when applied for vTEC forecasting are depicted in Fig. 8 for horizons ranging between 1 and 6 hours. Generally the minimum SD of the error distribution is achieved by using MSE_v1 in the ANN model across all the forecasting horizons.

Fig. 8
figure 8

Error distribution of the model with different loss functions on the test dataset, which are clustered around zero with a small dispersion

Full size image
Table 8 Evaluation of our proposed ANN architecture on the test dataset using different loss functions
Full size table

We make use of SD for evaluating the performance of the ANN models on the test dataset, using the different loss functions, to forecast vTEC between 1 and 24 hours in advance. From Table 8, the best mean SD is obtained when MSE_v1 is used (0.4240 TECU), followed by MSE_v4 with a mean SD of 0.4258 TECU while MSE_v2, MSE_v5, MSE_v3, and MSE_v0 achieve a mean SD of 0.4271 TECU, 0.4275 TECU, 0.4277 TECU, and 0.4278 TECU, respectively. Therefore, all five physics-informed loss functions performs better than the standard MSE_v0 loss function.

Fig. 9
figure 9

Box-and-Whisker plots for the evaluation of the ANN models performance using different loss functions

Full size image
Fig. 10
figure 10

Quiet Event (4-6 August 2018). The plot shows the actual and the predicted values of vTEC, from trained ANN models using MSE_V0 and MSE_V1

Full size image
Fig. 11
figure 11

Stormy Event (24-26 August 2018). The plot shows the actual and the predicted values of vTEC, from trained ANN models using MSE_V0 and MSE_V1

Full size image

Due to the sensitivity of the statistic mean to outliers, we use a box-and-whisker plot (non-parametric) to further evaluate the forecasting performance of the ANN models (using different loss-functions) on the testing dataset. According to Fig. 9, MSE_v3, MSE_v1, MSE_ v4, MSE_v2, MSE_v0, and MSE_v5, produce the least variability (in ascending order) in the ANN models performance, highlighted by the box’s width and their confidence levels. The performance distribution based on the use of MSE_v0, MSE_v2, and MSE_v4 exhibits a positive skewness, with the presence of outliers in each case. With MSE_v1 we gain the greatest median value of \(R^2= 0.801\), followed by MSE_v4 and MSE_v5 both reaching median \(R^2\) of 0.797. Both MSE_v0 and MSE_v3 obtain \(R^2\) median values of 0.796, and MSE_v2 has the lowest median \(R^2\) of 0.795.

To assess whether the improvements given by the physics-informed loss functions used in the learning phase of the ANN model are statistically significant, the Wilcoxon non-parametric signed ranked test has been performed. We select a significance level \(\alpha =0.05\) and evaluate the probability (p-value) that the improvement of one ANN model in respect to another is given or not by chance. The assumption that the improvement is not given by chance is satisfied when p-value \(< \alpha \). The ANN model trained with the MSE_v1 is much better at predicting vTEC over time than the ANN models trained with MSE_v0, MSE_v2, MSE_v3, MSE_v4 and MSE_v5.

Table 9 Wilcoxon non-parametric signed ranked test compares the performance of the ANN models using different loss functions
Full size table

As much as the evaluation metrics show how the predicted vTEC deviates from the actual vTEC, Figs. 10 and 11 show a snippet of the models on the test dataset for quiet and stormy events, respectively, as derived from (https://www.spaceweather.com/). The stormy events from August 24 to August 26, 2018 were deeply investigated in Akala et al. (2021). The storm on August 26, 2018 is a G3 geomagnetic storm, the third largest geomagnetic storm of solar cycle 24, driven by the aggregation of the Coronal Mass Ejection (CME) transient, initiated by the solar filament eruption on August 20. On August 21, CME left the solar corona and buffeted the Earth’s magnetosphere with two minor shocks at 06:45 UT and 08:00 UT on August 24 and 25, respectively, with weak sheath fields behind them Akala et al. (2021). G3 characterises the magnitude of the geomagnetic storm, and this is measured by using the Planetary K-index (Kp), which is an indicator of disturbance in the horizontal component of the Earth’s magnetic field ranging from 0 to 9, with 1 being calm and 5 or more indicating a geomagnetic storm, in accordance with the National and Atmospheric Administration’s (NOAA) scale. In particular, the storm on August 26 has a Kp of 7.

As expected, in quiet events, the model gives better results as compared to stormy events and performs worse as the forecasting horizon increases. An example of decreasing model performance with increasing the forecasting horizon can be seen in Fig. 10 (quiet period) at 15 and 18 hours in advance. In Fig. 11, obtained for the stormy event on 24-26 August 2018, the model performance strongly decreases starting at 4 hours forecasting horizon: the model is not able to capture the vTEC positive storm of several TECu on August 26, when the G3 storm occurred.

Conclusions and future work

In this paper, we evaluate the performance of ANN predictive models trained with five physics-informed loss functions introduced to overcome a drawback when training uses standard loss functions for vTEC forecasting. In fact a multivariate machine learning model also learns appreciably well the quiet events besides the stormy events available in the training dataset and physics-informed loss functions would help to adapt the training in function of the geospatial disturbance level. These five physics-informed loss functions are:

  • MSE_v1: It makes use of the Dst and Bz indices to detect stormy events and switches between using the standard loss (MSE) for quiet events and using the loss function with the imposed Dst and Bz constraints for stormy events. Overall, this is the best among all the physics-informed loss functions developed, and the standard loss function shows a significant improvement, as shown in Table 9 using the Wilcoxon signed ranked test with a significance level of \(\alpha = 0.05\). In addition, in the training, validation, and testing phases of the model with the loss function MSE_v1, outperforms the versions using the other loss functions under discussion, with the minimum mean of SD depicted in Table 6, Table 7, and Table 8, respectively.

  • MSE_v2: It also uses the Dst and Bz indices and combines the standard loss function MSE with the Dst and Bz by looking at the sign of the derivative of Bz over an hour. In general, MSE_v2 is the second-best physics-based loss function in terms of the spread of error in the training phase depicted in Table 6. It is the worst in the validation phase (see, Table 7) and the third-best in the testing phase (see, Table 8) of the ANN model, but the improvement is not significant as illustrated in Table 9.

  • MSE_v3: It takes into account the predicted impact on the near-Earth space of the coupling function, including the external indices v, By, Bz and \(B_{T}\), as a constraint to penalise the classical squared loss function. On the descriptive plot in Fig. 9, the Box-and-Whisker plot (non-parametric), shows the minimum spread of the ANN models performance across all the loss functions on the test dataset but with no significant improvement.

  • MSE_v4: It comprises the Dst, Bz, and coupling functions as a constraint imposed on the standard MSE. On the test dataset, the ANN model using the MSE_v4 loss function was the second best on average across all forecasting horizons in terms of the spread of prediction error but added no significant improvement (see Table 8 and 9).

  • MSE_v5: This combines MSE v1 and MSE v3 on a conditional basis by using the sign of the derivative of Bz. It had the greatest spread of the ANN models performance on the test dataset, according to Fig. 9.

The proposed ANN model making use of the MSE_v1 outperforms, for both quiet and stormy events and in all phases of the machine learning algorithm, the ANNs fed by the other phsics-informed loss functions under test, including the standard squared error loss function (MSE_v0).

In addition, the loss function MSE_v1 shows a significant performance improvement on the test dataset at different forecasting horizons, such as 1-8, 10-13, 15-17, and 19-24 hours ahead, as compared to the MSE_v0, although the performance of all models decreases as forecasting horizons increase above all during stormy events. Future work includes: 1) re-design of physics-informed loss function by incorporating more physical mechanisms and also considering other (external) parameters (e.g., ionospheric indices in Cesaroni et al. (2020)) to increase the ANN performance as forecasting horizon increase, particularly during geospatial disturbed conditions, 2) applying the ANN model with the newly designed physics-informed loss function at different latitudes to lay the foundation for the development of an ANN global model, and 3) extend the use of physics-informed loss function to other neural network techniques, e.g. Recurrent Neural Network and its variant, transformers etc.