Abstract
High-resolution sensors onboard satellites are generally reputed for rapidly producing land-use/land-cover (LULC) maps with improved spatial detail. However, such maps are subject to uncertainties due to several factors, including the training sample size. We investigated the effects of different training sample sizes (from 1000 to 12,000 pixels) on LULC classification accuracy using the random forest (RF) classifier. Then, we analyzed classification uncertainties by determining the median and the interquartile range (IQR) of the overall accuracy (OA) values through repeated k-fold cross-validation. Results showed that increasing training pixels significantly improved OA while minimizing model uncertainty. Specifically, larger training samples, ranging from 9000 to 12,000 pixels, exhibited narrower IQRs than smaller samples (1000–2000 pixels). Furthermore, there was a significant variation (Chi2 = 85.073; df = 11; p < 0.001) and a significant trend (J-T = 4641, p < 0.001) in OA values across various training sample sizes. Although larger training samples generally yielded high accuracies, this trend was not always consistent, as the lowest accuracy did not necessarily correspond to the smallest training sample. Nevertheless, models using 9000–11,000 pixels were effective (OA > 96%) and provided an accurate visual representation of LULC. Our findings emphasize the importance of selecting an appropriate training sample size to reduce uncertainties in high-resolution LULC classification.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Land use/land cover (LULC) are fundamental aspects of the Earth’s system that are intricately linked to numerous anthropogenic activities and the physical environment (Aune-Lundberg and Strand 2014; Chatziantoniou et al. 2017; Mazeka et al. 2021; Gudmann and Mucsi 2022). Therefore, obtaining precise information regarding LULC is of utmost importance for effectively mapping and monitoring LULC in operational settings (Bui and Mucsi 2022). An essential and first step towards LULC planning is the availability of spatial information, traditionally obtainable from aerial photographs. Although aerial photos offer a relatively high spatial resolution, which allows for detailed LULC information acquisition, their visual interpretation can be time-consuming and challenging over large areas (Nagel and Yuan 2016; Padmanaban et al. 2019; Pawłuszek et al. 2019).
Remote sensing data onboard satellites are increasingly used because they can acquire LULC information over broad geographical coverage and at the least cost (Khatami et al. 2016; Topaloğlu et al. 2016). Additionally, this widespread use of satellite data is fueled by the continuous improvement in sensor technology (Huang and Asner 2009), which has seen the emergence of high-resolution sensors and machine learning in the past few decades. However, despite these technological advances, accurate LULC mapping remains challenging because high-resolution LULC is inherently complex, comprising numerous categories with high intra-class spectral heterogeneity (Jia et al. 2018). Failure to define an optimal training sample size may exacerbate this challenge.
Characteristics of the training sample, particularly its size (n), are crucial to LULC classification and can potentially undermine the accuracy of the final LULC product owing to related uncertainty during the training stage of supervised learning (Ustuner et al. 2016). Additionally, in instances where the number of training data is limited or where constraints in processing power or time restrict the number of training samples that can be processed, it could be essential to recognize the relative dependence of a classifier on sample size (Ramezan et al. 2021). Consequently, an emphasis is increasingly placed on the importance of training sample size in LULC classification, as reflected in past research (Foody et al. 2006; Myburgh and Van Niekerk 2013; Millard and Richardson 2015; Qian et al. 2015). However, despite this emphasis, detailed analysis of the training sample size effect on the accuracy of LULC classification using random forest (RF) and high-resolution sensors remains poorly understood because most previous investigations used coarse or medium spatial resolution sensors like Landsat and Sentinel or were limited to crop and vegetation classification. For example, Thanh Noi and Kappas (2017) and Bobalova et al. (2021) examined the influence of the training sample size on accuracy using Sentinel-2 data, while Myburgh and Van Niekerk (2013) and Shang et al. (2018) used Landsat images. Podsiadlo et al. (2021) introduced an approach using the Copernicus Global Land Service - Land cover (CGLS-LC) map along with Sentinel-2 data to define a representative training dataset that can be employed to generate land cover maps at a large scale.
Only a few studies used high spatial resolution images; however, such studies did not involve RF or investigate different aspects of training data. For example, Ustuner et al. (2016) used high spatial resolution RapidEye images but different machine learning algorithms other than RF. Even so, their study focused on the effect of balanced and imbalanced training sample sizes on classification accuracy, an approach similar to that of Burai et al. (2015). A recent study by Ebrahimy et al. (2021) provided a detailed analysis of RF classification across three study sites using both high (Ikonos) and medium (Sentinel and Landsat) spatial resolution images. However, their study was based on a limited and fixed training sample size (n > 400) in each study site. Ramezan et al. (2021) used high spatial resolution (up to 1 m) images, including a United States National Agriculture Imagery Program (NAIP) and light detection and ranging (LIDAR) data. However, this study considered only four broad LULC classes, thus limiting our understanding of the relationship between the training sample size and classification accuracy in environments with numerous, diverse and complex LULC types. Furthermore, the optical and LiDAR data used in that study are not readily available or may be unaffordable to acquire for most parts of the world, especially data-poor regions. Shao et al. (2021) employed two deep convolutional neural networks on a WorldView image to investigate the impact of varying sample sizes or image tiles on the accuracy of mapping LULC. Similarly, Luo et al. (2020) introduced a hybrid convolutional neural network (H-ConvNet) to enhance urban land cover mapping using Sentinel-2 images and presented a technique to augment training samples. Although these studies highlight the efficacy of deep convolutional networks in remote sensing, these networks were originally designed for large-scale image recognition and often require a vast amount of training data (Krizhevsky et al. 2012). The necessity to obtain such extensive training data manually, especially in remote sensing, is a significant challenge. Although there is momentum toward automated labeling of LULC categories from remotely sensed data (Matcı and Avdan 2022), determining the ideal sample size is still essential.
Therefore, this study investigated the effect of the training sample size on the accuracy of LULC classification using the RF algorithm and Systeme Pour l’Obsevation de la Terre (SPOT-7) multispectral data. Our emphasis is on quantifying and examining the uncertainties associated with the classification accuracy yielded by the RF algorithm across varying training sample sizes. We evaluated the uncertainties by identifying the median and the interquartile range (IQR) of the overall accuracy (OA) values using repeated k-fold cross-validation. Specifically, we addressed the following research questions: (i) do the medians of OA values come from the same distribution; (ii) do the OAs significantly vary with the size of training samples; and (iii) is there any significant trend between accuracy and training sample size?
Materials and methods
Study area
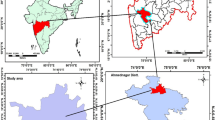
We selected Kokstad as a study area, a small city in South Africa lying on the boundary between KwaZulu-Natal (KZN) and Eastern Cape provinces, stretching from 30º 29’ 30.54” and 30º 36’ 38.59” latitudes to 29º 22’ 52.83” and 29º 28’ 48.82” longitudes (Fig. 1). The city covers a surface area of approximately 94 km², with a population of 65,981 people (Statistics South Africa 2016). The climate is humid, with annual rainfall ranging from 600 mm to over 1000 mm. Most of the rain occurs in summer, from November to January. The average yearly temperature typically ranges from 6 to 15 °C. The urban settlement, transport network, recreational parks, business and commerce, and commercial crop cultivation and livestock farming are major LULC types in the study area. This complex structure of LULC makes the area ideal for this investigation.
Image acquisition and preprocessing
SPOT-7 multispectral image (16 April 2016) was obtained free of charge for the study area from the South African National Space Agency (SANSA). A cloud-free image consisting of four multispectral bands with a spatial resolution of 5.5 m: blue (450–525 nm), green (530–590 nm), red (625–695 nm), and near infra-red (760–890 nm), including a panchromatic band (450–745 nm) at 1.5 m spatial resolution. The images were already geometrically corrected by the suppliers. Currently, the SNAP toolbox does not support atmospheric correction for SPOT-7 data (Gascon and Ramoino 2017), so the atmospheric correction involving adjusting reflectance values or brightness to a common illumination condition was performed in ArcMap 10.4 using the Apparent Reflectance function (ESRI 2022). This function minimizes the brightness variation between scenes of different solar illumination angles.
Defining Land Use/Cover (LULC) classes
A USGS-based LULC classification system developed by (Anderson 1976) was used to define LULC classes. This classification system consists of four levels of classifying LULC from a remotely sensed image (Jensen and Cowen 1999) ranging from broad (Level I) to detailed (Level IV) LULC classifications. Considering the spatial resolution of the SPOT-7 image, the LULC classes were defined based on the first two levels (Level I and II), resulting in nine categories (Table 1).
Experiments on LULC classification
We classified LULC using the RF classifier (Breiman 2001) because of its high classification accuracy, as reported in previous LULC studies (Ma et al. 2017; Talukdar et al. 2020; Bobalova et al. 2021; Ramezan et al. 2021). Furthermore, unlike parametric algorithms, RF does not assume the normal distribution of data, making it an ideal candidate for classifying remotely sensed data, which rarely, if ever, have normal distributions (Belgiu and Drăgu 2016). RF is based on an ensemble of decision trees and combines the predictions from all trees where each decision tree contributes a single vote to a classification of a particular class (Cutler et al. 2007; Maxwell et al. 2019). The final class is then determined based on the majority rule (Breiman 2001; Liaw and Wiener 2002). RF models were trained with 500 trees (ntree) and varying training samples (1000–12,000 pixels).
Reference data were collected using polygons digitized in ArcGIS Desktop 10.4 (ESRI 2022) based on a visual interpretation of Google Earth and a high-resolution (1.5 m) panchromatic SPOT-7 image. The polygons were exported to the R software (R Core Team 2021) where points were generated for extracting reference pixels corresponding to each LULC. Training pixels representing at least 0.25% of the study area are often recommended (Thanh and Kappas 2017). Polygons covered 90,145 pixels for training data (0.32% of the entire study area), but we did not use the whole set: a maximum of 12,000 pixels were involved. Experiments that revealed the role of the number of training pixels in RF classifications were performed on 12 training sample sizes ranging from 1000 to 12,000 pixels (1000-pixel intervals, i.e. 1000, 2000, 3000, … 12,000). We intended to keep the ratio of training pixels related to all reference data under 15% to decrease the chance of using adjacent pixels as training and testing to ensure independent data avoiding spatial autocorrelation (Abriha et al. 2023). Classifications were performed by randomly splitting the reference data to 50% training and 50% testing. OA and class-level metrics, the producer’s accuracy (PA), and user’s accuracy (UA) were computed (Congalton 1991).
All models have uncertainties, and our goal was to quantify them following a three-step procedure. Firstly, we repeated all model runs, performing stratified random selections nine times by land cover classes. Second, we conducted the RF classification on each training sample (1000–12,000 pixels) with 10-fold cross-validation repeated three times. Finally, we had 9 (random selections) × 30 (10-fold cross-validation with three repetitions) × 12 (classifications using 1000–12,000 training pixels), resulting in 3240 models to be evaluated. Classification uncertainties were analyzed by measuring the medians and interquartile range (IQR) of model repetitions’ OA values determined with the k-fold cross-validation. The IQR is a good indicator of model stability. Specifically, a narrow IQR indicates lower uncertainty, suggesting that several model iterations do not bias the accuracy.
Classifications were executed in R 4.2.2. (R Core Team 2021) with the caret and rpart packages (Kuhn et al. 2023; Therneau et al. 2022). We employed the ‘grid search’ method for hyperparameter tuning, testing the mtry parameter (representing the number of randomly selected variables at each split) with values ranging from 1 to 20. Predictions were performed on all models (rf1 - rf12) with the most optimal parameters, as determined by the grid search combined with k-fold cross-validation. We also computed class-level accuracies, assessing the average outcomes of these repeated runs. This involved visual interpretation of the results by plotting UAs and PAs on a scatterplot. Furthermore, based on their respective confusion matrices, we contrasted the best models derived from the smallest (1000 pixels, rf1) and largest (12,000 pixels, rf12) training samples. In this context:
-
Diagonal values represented pixels consistently classified under the same categories by both models.
-
Rows in the contingency table illustrated scenarios where the rf12 model identified specific pixels differently than the rf1 model. The error of commission (EoC) was calculated as the diagonal value relative to the sum of differing classifications.
-
Columns of the table depicted pixels omitted by rf1 but captured by rf12. The error of omission (EoO) was represented as the diagonal value over the total omitted pixels.
We observed the spatial differences across model predictions from different training sizes by adding up all the built-up areas (from rf1-rf12) as a binary raster layer. The frequency of correct classifications was displayed, with darker shades indicating how often built-up area pixels were correctly identified. If no model detected the built-up area pixel, the value was 0; if all models identified it correctly, the value was 12.
Statistical analysis
We used the Kruskal-Wallis (Kruskal and Wallis 1952) and Jonckheere-Terpstra (Terpstra 1952; Jonckheere 1954) tests to investigate the statistical significance of differences in the relationship between OA and training sample size. The hypotheses for the Kruskal-Wallis test were: H0: there is no statistically significant difference among the OAs and training sample sizes. Concerning the Jonckheere-Terpstra test, the H0 assumed that there was no significant trend of OAs by increasing the number of training pixels.
Results and discussion
Accuracy and uncertainties
Although even the lower quartile for OAs exceeded 0.94, the IQRs were notably larger for training samples of 1000 and 2000 pixels, suggesting a high variance in OA values (Fig. 2). Best accuracies surpassed 0.96; however, among the top performances, models with 12,000 training pixels only appeared twice out of the nine instances, with the highest accuracies spanning models from 9000 to 12,000 pixels. Notably, models with 9000 and 10,000 pixels secured the top position three times. Typically, a training size of 5000 pixels was sufficient to achieve a high OA with minimal variability.
The larger training samples generally resulted in more accurate classification outcomes. This trend was particularly evident for smaller training sample sizes. However, when the sample size exceeded 6000 training pixels, the highest accuracies varied, with the most optimal OAs observed for models using between 9000 and 11,000 training pixels (Fig. 3a). Kruskal-Wallis test confirmed these differences to be significant (Chi2 = 85.073; df = 11; p < 0.001). The Jonckheere-Terpstra test also revealed a significant trend (J-T = 4641, p < 0.001), suggesting that the training sample size significantly influenced the OA. Although the differences in OAs were marginal, we observed the smallest variability in classifications with training samples of 11,000 and 12,000 pixels (Fig. 3). These findings align with prior research (Burai et al. 2015; Ramezan et al. 2021), which found that RF classifications benefit from a larger training sample size. Bobalova et al. (2021) and Millard and Richardson (2015) also recommended maximizing the training sample size in RF classifications. Conversely, Heydari and Mountrakis (2018) and, more recently Higgs and van Niekerk (2022) argued that while increasing training samples enhances classification accuracy, there is a threshold beyond which no further improvements are observed. In our study, although there was a general trend of increased OAs with larger training samples, we observed instances where models trained on smaller datasets outperformed those with more extensive training pixels. Consequently, the association between training sample size and accuracy was not always linear. Furthermore, we found that the median OA values fit a second-order polynomial curve (R2 = 0.943, F = 74.471, p < 0.001; Eq. 1), suggesting distinct distributions for these median values.
OAp = -0.0002591 × 2 + 0.005053x + 0.9576 (Eq. 1).
where OAp is the predicted overall accuracy, and x is the number of training pixels per 1000 (i.e., 1–12).
Besides, a larger number of training pixels decreased the uncertainty, and the IQR of the models was significantly smaller (Fig. 3b); according to the Jonckheere-Terpra test, there was a significant decrease (J-T = 910, p < 0.001).
Class-level analysis of accuracy by LULC types
Concerning class accuracies (PA and UA), we generally found the most substantial agreements in the classifications where the training samples were the largest, but there were some exceptions, where some classes with smaller training pixels achieved high accuracies (Fig. 4). Another observation is that no specific LULC class had the lowest accuracy in all models, meaning the worst classification accuracy belonged to different LULC classes in each model. An increase in training sample size did not correspondingly result in a significant improvement in PA in our study. To provide further clarity, it is important to note that the PA exhibited variability instead of a consistent upward trajectory as the training sample size increased. Ramezan et al. (2021) reported an increase in both PAs and UAs for minority classes as the sample size increased. Cheng et al. (2021) found that the behavior of UA is influenced by the distribution of training data across distinct LULC categories, whereas PA demonstrated minimal variation when presented with larger training samples. To some extent, our findings align with these studies, particularly regarding UA. This alignment is underscored by the consistent upward trend observed in UA for specific LULC classes. An example is the built-up area (BA), which began with UA values below 50% and exhibited a sustained increase, eventually exceeding 95%.
Class accuracy metrics of LULC classification based on different training sample sizes (F: forest, P: plantation, GG: green grass, DG: dry grass, SF: sports fields/parks, BA: built-up areas, WS: wet soil, DS: dry soil, WB: water bodies, the upper right section with black-dotted lines indicates > 85% accuracy quarter)
The visual analysis of the classification results revealed that increased training sample size improved the LULC classification (Fig. 5). For example, models (rf1-rf7) trained on smaller samples (1000–7000 pixels) frequently misclassified small water bodies (WB) found in the northern and western parts of the study area. This underperformance was further substantiated by the lowest PA (77–80%) values for the WB class (Fig. 4), indicating substantial omission errors. Another visually relevant error was misclassifying the built-up areas as the dry grass (DG), dry soil (DS), and wet soil (WS) classes. On the contrary, models (rf11-rf12), trained on considerably larger training samples (11,000–12,000 pixels), showed better and consistent classification results. Shang et al. (2018) similarly observed a correlation between increased training sample sizes and the accurate visual representation of LULC.
Comparing rf1 and rf12 revealed inconsistencies, quantified with EoC and EoO (Table 2). Rf12 showed the best class accuracy values, while rf1 showed the lowest accuracy, allowing us to distinguish class-level discrepancies. Notably, the highest misclassification rates by rf1 (EoC) were detected in the BA and SF classes. Furthermore, rf1 exhibited a substantial EoO, exceeding 200% for the WB, P, and DS classes. Despite these primary discrepancies, it was evident that disagreements were essentially pronounced, with exceptions in a few categories, such as P and WB (which had an EoC of up to 5%) and SF (with an EoO of 1%). Interestingly, where EoC was minimal, EoO increased, as seen in the case of P, where EoC was 79% while EoO reached 294%. Visual inspection and class-based evaluation highlighted that, although OAs good, there were significant misclassifications with 1000 training pixels. Specifically, for the BA category, the results across the 12 training sample sizes differed significantly, with no consistent trend (Fig. 6). Furthermore, there was a considerable number of misclassified pixels in this LULC category, with an EoC of 349%.
These findings demonstrate that spectral confusion is a prevalent issue in LULC classification, especially when using a multiclass approach. While binary classification, which categorizes LULC into two classes, offers simplicity and is easier to interpret, it is often best suited for areas with predominant, homogenous LULC types. Our study area, characterized by various heterogeneous LULC classes, presents challenges for this approach. One could consider merging these classes to address intra-class spectral confusion, particularly between WS, DS, and BA. However, our focus was to assess the impact of varying sample sizes on intra- and inter-class classification accuracy. Given that regions with considerable intra-class variability may demand more extensive training samples than areas with the opposite characteristics (Van Niel et al. 2005), up-sampling to augment training data for underrepresented LULC classes may be a viable solution. Nonetheless, this lies outside our current study’s scope. As such, in-depth studies are required on the implications of resampling techniques, both up-sampling and down-sampling for the classification accuracy of underrepresented classes.
Our research focused on the influence of training sample size on classification accuracy. However, many factors, such as sample design, quality, chosen algorithm, and the specifics and composition of the study region play an important role in the accuracy (Foody et al. 2006; Ustuner et al. 2016). Regardless of these influencing factors, our analysis offered valuable insights into how training sample size impacts classification accuracy within our chosen training sample range (n = 1000–12,000 pixels). Training sample sizes between 9000 and 11,000 pixels exhibited high effectiveness, achieving an OA of over 96%. Conventionally, an OA exceeding 85% is deemed adequate for LULC classification (Landis and Koch 1977; Everitt et al. 2008). Given this threshold and the minimal OA variance in models trained with 9000–11,000 pixels, we infer that this pixel range may be the ideal sample size for achieving accurate LULC classification outcomes, at least based on our study’s parameters. Yet, this assertion should be considered by accounting for other determinants of classification accuracy, such as the study area’s size, LULC composition, and the spatial resolution of the employed satellite imagery. While there are inherent challenges in drawing broad conclusions due to the variability in data and study sites (Van Niel et al. 2005), valuable insights can be gained from our study. Although the expansion of training samples usually improves classification accuracy, further research must determine a threshold at which additional samples cannot further increase the accuracy of different classifiers, satellite images, and environmental settings.
Conclusions
This study investigated the impact of different training sample sizes on the classification accuracy of LULC. We assessed classification uncertainties by computing the median IQR of the OA values through multiple iterations of k-fold cross-validation. This method enhances model robustness and effectively reduces the propensity for overfitting, a frequent issue in remote sensing. Corroborated by statistical analysis, our findings showed that larger training sample sizes generally resulted in higher classification accuracies (OA > 96%), and ensured a precise visual depiction of LULC. Additionally, the median OA values significantly differed across training sample sizes, with larger samples exhibiting low OA variance, suggesting that determining the appropriate training sample size can minimize uncertainties in high-resolution LULC classification. While this research advocates for identifying an ideal training sample size, it is crucial to account for the specific attributes of the study area, including its overall scale and LULC composition, as well as the details of the remote-sensing data (particularly, spectral and spatial resolutions), since these can also impact classification outcomes. Overall, our findings can potentially enhance LULC mapping and monitoring endeavors in comparable operational settings.
Data Availability
The data presented in this study are available on request from the corresponding author.
References
Abriha D, Srivastava PK, Szabó S (2023) Smaller is better? Unduly nice accuracy assessments in roof detection using remote sensing data with machine learning and k-fold cross-validation. Heliyon 9:1–17. https://doi.org/10.1016/j.heliyon.2023.e14045
Anderson JR, Hardy EE, Roach JT, Witmer RE (1976) A land use and land cover classification system for use with remote sensor data. US Geol Surv Prof Paper 964:28
Aune-Lundberg L, Strand G-H (2014) Environ Model Softw 61:87–97. https://doi.org/10.1016/j.envsoft.2014.07.001. Comparison of variance estimation methods for use with two-dimensional systematic sampling of land use/land cover data
Belgiu M, Drăgu L (2016) Random forest in remote sensing: a review of applications and future directions. ISPRS J Photogrammetry Remote Sens 114:24–31. https://doi.org/10.1016/j.isprsjprs.2016.01.011
Bobalova H, Benová A, Kožuch M (2021) Hierarchical object-based mapping of Urban Land Cover using Sentinel-2 data: a case study of six cities in Central Europe. PFG–Journal of Photogrammetry Remote Sensing and Geoinformation Science 89:15–31. https://doi.org/10.1007/s41064-020-00135-8
Breiman L (2001) Random forests. Mach Learn 45:5–32. https://doi.org/10.1023/A:1010933404324
Bui DH, Mucsi L (2022) Predicting the future land-use change and evaluating the change in landscape pattern in Binh Duong province, Vietnam. Hung Geographical Bull 71:349–364. https://doi.org/10.15201/hungeobull.71.4.3
Burai P, Deák B, Valkó O, Tomor T (2015) Classification of herbaceous vegetation using airborne hyperspectral imagery. Remote Sens 7:2046–2066. https://doi.org/10.3390/rs70202046
Chatziantoniou A, Petropoulos GP, Psomiadis E (2017) Co-Orbital Sentinel 1 and 2 for LULC mapping with emphasis on wetlands in a mediterranean setting based on machine learning. Remote Sens 9:1259. https://doi.org/10.3390/rs9121259
Cheng KS, Ling JY, Lin TW et al (2021) Quantifying uncertainty in Land-Use/Land-Cover classification accuracy: a Stochastic Simulation Approach. Front Environ Sci 9:1–18. https://doi.org/10.3389/fenvs.2021.628214
Congalton RG (1991) A review of assessing the accuracy of classifications of remotely sensed data. Remote Sens Environ 37:35–46. https://doi.org/10.1016/0034-4257(91)90048-B
Cutler DR, Edwards TC Jr, Beard KH et al (2007) Random forests for classification in ecology. Ecology 88:2783–2792. https://doi.org/10.1890/07-0539.1
Ebrahimy H, Mirbagheri B, Matkan AA, Azadbakht M (2021) Per-pixel land cover accuracy prediction: a random forest-based method with limited reference sample data. ISPRS J Photogrammetry Remote Sens 172:17–27. https://doi.org/10.1016/j.isprsjprs.2020.11.024
ESRI (2022) ArcGIS Desktop Software (Version 10.4)
Everitt JH, Yang C, Fletcher R, Deloach CJ (2008) Comparison of QuickBird and SPOT 5 satellite imagery for mapping giant reed. J Aquat Plant Manag 46:77–82
Foody GM, Mathur A, Sanchez-Hernandez C, Boyd DS (2006) Training set size requirements for the classification of a specific class. Remote Sens Environ 104:1–14. https://doi.org/10.1016/j.rse.2006.03.004
Gascon F, Ramoino F (2017) Sentinel-2 data exploitation with ESA’s Sentinel-2 Toolbox. In: EGU General Assembly Conference Abstracts. p 19548
Gudmann A, Mucsi L (2022) Pixel and object-based Land Cover Mapping and Change Detection from 1986 to 2020 for Hungary using Histogram-based gradient boosting classification Tree Classifier. Geogr Pannonica 26:165–175. https://doi.org/10.5937/gp26-37720
Heydari SS, Mountrakis G (2018) Effect of classifier selection, reference sample size, reference class distribution and scene heterogeneity in per-pixel classification accuracy using 26 landsat sites. Remote Sens Environ 204:648–658. https://doi.org/10.1016/j.rse.2017.09.035
Higgs C, van Niekerk A (2022) Impact of Training Set Configurations for differentiating Plantation Forest Genera with Sentinel-2 Imagery and Machine Learning. Remote Sens 14:3992. https://doi.org/10.3390/rs14163992
Huang C, Asner GP (2009) Applications of remote sensing to alien invasive plant studies. Sensors 9:4869–4889. https://doi.org/10.3390/s90604869
Jensen JR, Cowen DC (1999) Remote sensing of urban/suburban infrastructure and socio-economic attributes. Photogramm Eng Remote Sensing 65:611–622
Jia Y, Ge Y, Ling F et al (2018) Urban land use mapping by combining remote sensing imagery and mobile phone positioning data. Remote Sens 10:446. https://doi.org/10.3390/rs10030446
Jonckheere AR (1954) A distribution-free k-sample test against ordered alternatives. Biometrika 41:133–145. https://doi.org/10.2307/2333011
Khatami R, Mountrakis G, Stehman SV (2016) A meta-analysis of remote sensing research on supervised pixel-based land-cover image classification processes: General guidelines for practitioners and future research. Remote Sens Environ 177:89–100. https://doi.org/10.1016/j.rse.2016.02.028
Krizhevsky A, Sutskever I, Hinton GE (2012) ImageNet Classification with Deep Convolutional Neural Networks. In: Advances in Neural Information Processing Systems 25. pp 1–9
Kruskal WH, Wallis WA (1952) Use of ranks in one-criterion variance analysis. J Am Stat Assoc 47:583–621. https://doi.org/10.1080/01621459.1952.10483441
Kuhn M, Wing S, Weston A, Williams C et al (2023) Caret: classification and regression training. R Package Version 6:0–94. https://github.com/topepo/caret/
Landis JR, Koch GG (1977) The measurement of observer agreement for categorical data. Biometrics 33:159–174. https://doi.org/10.2307/2529310
Liaw A, Wiener M (2002) Classification and regression by randomForest. R news 2:18–22
Luo X, Tong X, Hu Z, Wu G (2020) Improving urban land cover/use mapping by integrating a hybrid convolutional neural network and an automatic training sample expanding strategy. Remote Sens 12:2292. https://doi.org/10.3390/rs12142292
Ma L, Li M, Ma X et al (2017) A review of supervised object-based land-cover image classification. ISPRS J Photogrammetry Remote Sens 130:277–293. https://doi.org/10.1016/j.isprsjprs.2017.06.001
Matcı DK, Avdan U (2022) Data-driven automatic labelling of land cover classes from remotely sensed images. Earth Sci Inform 15:1059–1071. https://doi.org/10.1007/s12145-022-00788-6
Maxwell AE, Strager MP, Warner TA et al (2019) Large-Area, high spatial Resolution Land Cover Mapping using Random forests, GEOBIA, and NAIP Orthophotography: findings and recommendations. Remote Sens 11:1409. https://doi.org/10.3390/rs11121409
Mazeka B, Phinzi K, Sutherland C (2021) Monitoring changing Land Use-Land Cover Change to reflect the impact of Urbanisation on Environmental Assets in Durban, South Africa. Sustainable Urban futures in Africa. Routledge, pp 132–158. https://doi.org/10.4324/9781003181484-7
Millard K, Richardson M (2015) On the importance of training data sample selection in random forest image classification: a case study in peatland ecosystem mapping. Remote Sens 7:8489–8515. https://doi.org/10.3390/rs70708489
Myburgh G, Van Niekerk A (2013) Effect of feature dimensionality on object-based land cover classification: a comparison of three classifiers. South Afr J Geomatics 2:13–27
Nagel P, Yuan F (2016) High-resolution land cover and impervious surface classifications in the twin cities metropolitan area with NAIP imagery. Photogramm Eng Remote Sensing 82:63–71. https://doi.org/10.14358/PERS.83.1.63
Padmanaban R, Bhowmik AK, Cabral P (2019) Satellite image fusion to detect changing surface permeability and emerging urban heat islands in a fast-growing city. PLoS ONE 14:1–20. https://doi.org/10.1371/journal.pone.0208949
Pawłuszek K, Marczak S, Borkowski A, Tarolli P (2019) Multi-aspect analysis of object-oriented landslide detection based on an extended set of LiDAR-derived terrain features. ISPRS Int J Geoinf 8:321. https://doi.org/10.3390/ijgi8080321
Podsiadlo I, Paris C, Bruzzone L (2021) An approach based on low resolution land-cover-maps and domain adaptation to define representative training sets at large scale. In: International Geoscience and Remote Sensing Symposium (IGARSS). Institute of Electrical and Electronics Engineers Inc., pp 313–316. https://doi.org/10.1109/IGARSS47720.2021.9553498
Qian Y, Zhou W, Yan J et al (2015) Comparing machine learning classifiers for object-based land cover classification using very high resolution imagery. Remote Sens 7:153–168. https://doi.org/10.3390/rs70100153
R Core Team (2021) R: a language and environment for statistical computing. R Foundation for statistical computing, Vienna
Ramezan CA, Warner TA, Maxwell AE, Price BS (2021) Effects of training set size on supervised machine-learning land-cover classification of large-area high-resolution remotely sensed data. Remote Sens 13:368. https://doi.org/10.3390/rs13030368
Shang M, Wang S-X, Zhou Y, Du C (2018) Effects of Training samples and classifiers on classification of Landsat-8 imagery. J Indian Soc Remote Sens 46:1333–1340. https://doi.org/10.1007/s12524-018-0777-z
Shao Y, Cooner AJ, Walsh SJ (2021) Assessing deep convolutional neural networks and assisted machine perception for urban mapping. Remote Sens 13:1523. https://doi.org/10.3390/rs13081523
Statistics South Africa (2011) “Greater Kokstad Municipality”. https://www.statssa.gov.za/?page_id=993&id=greater-kokstad-municipality. Accessed on 22 August 2023
Talukdar S, Singha P, Mahato S et al (2020) Land-use land-cover classification by machine learning classifiers for satellite observations—a review. Remote Sens 12:1135. https://doi.org/10.3390/rs12071135
Terpstra TJ (1952) The asymptotic normality and consistency of Kendall’s test against trend, when ties are present in one ranking. Indagationes Math 14:327–333
Thanh NP, Kappas M (2017) Comparison of Random Forest, k-Nearest neighbor, and support Vector Machine Classifiers for Land Cover classification using Sentinel-2 imagery. Sensors 18:18. https://doi.org/10.3390/s18010018
Therneau T, Atkinson B, Ripley B (2022) rpart: Recursive partitioning and regression trees. R package version 4.1.19. https://cran.r-project.org/package=rpart
Topaloğlu RH, Sertel E, Musaoğlu N (2016) Int archives photogrammetry remote Sens Spat Inform Sci 41:12–49. https://doi.org/10.5194/isprsarchives-XLI-B8-1055-2016. assessment of classification accuracies of Sentinel-2 and landsat-8 data for land cover/use mapping
Ustuner M, Sanli FB, Abdikan S (2016) Balanced vs imbalanced training data: classifying RapidEye data with support vector machines. Int Archives Photogrammetry Remote Sens Spat Inform Sci 41:379–384. https://doi.org/10.5194/isprs-archives-XLI-B7-379-2016
Van Niel TG, McVicar TR, Datt B (2005) On the relationship between training sample size and data dimensionality: Monte Carlo analysis of broadband multi-temporal classification. Remote Sens Environ 98:468–480. https://doi.org/10.1016/j.rse.2005.08.011
Acknowledgements
We are very grateful to the South African National Space Agency (SANSA) for providing SPOT data at no cost.
Funding
Open access funding provided by University of Zululand. The research was funded by the NKFI K138079 and K138503 projects, Hungary.
Open access funding provided by University of Zululand.
Author information
Authors and Affiliations
Contributions
K.P.: Conceptualization, Methodology, Software, Data curation, Writing – original draft. NSN: Formal analysis, Writing – review & editing. Q.B.P., G.G.C.: review & editing. S.S.: Formal analysis, Writing – review & editing, Funding acquisition, Resources, Supervision.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Conflict of interest
On behalf of all authors, the corresponding author states that there is no conflict of interest.
Additional information
Communicated by H. Babaie.
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Phinzi, K., Ngetar, N.S., Pham, Q.B. et al. Understanding the role of training sample size in the uncertainty of high-resolution LULC mapping using random forest. Earth Sci Inform 16, 3667–3677 (2023). https://doi.org/10.1007/s12145-023-01117-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12145-023-01117-1