Impact of flight altitude and cover orientation on Digital Surface Model (DSM) accuracy for flood damage assessment in Murcia (Spain) using a fixed-wing UAV

Abstract

Soil erosion, rapid geomorphological change and vegetation degradation are major threats to the human and natural environment. Unmanned Aerial Systems (UAS) can be used as tools to provide detailed and accurate estimations of landscape change. The effect of flight strategy on the accuracy of UAS image data products, typically a digital surface model (DSM) and orthophoto, is unknown. Herein different flying altitudes (126-235 m) and area coverage orientations (N-S and SW-NE) are assessed in a semi-arid and medium-relief area where terraced and abandoned agricultural fields are heavily damaged by piping and gully erosion. The assessment was with respect to cell size, vertical and horizontal accuracy, absolute difference of DSM, and registration of recognizable landscape features. The results show increasing cell size (5-9 cm) with increasing altitude, and differences between elevation values (10-20 cm) for different flight directions. Vertical accuracy ranged 4-7 cm but showed no clear relationship with flight strategy, whilst horizontal error was stable (2-4 cm) for the different orthophotos. In all data sets, geomorphological features such as piping channels, rills and gullies and vegetation patches could be labeled by a technician. Finally, the datasets have been released in a public repository.

Introduction

Soil erosion and rapid geomorphological change are major threats to the environment and societal infrastructure in many regions of the world (Martin 1980).

Quantifying and monitoring geomorphological activity is challenging. While in-situ instruments are good tools for the acquisition of data of local activity, they often fail to provide the context that is required in order to understand the spatial dimension of a catchment or landscape (Smith and Pain 2009). Satellite imagery on the other hand is able to provide this spatial dimension, but may be very expensive or lack the detail and temporal resolution that is required to analyze at the scale that many soil erosion processes act (Iizuka et al. 2018).

The most common Unmanned Aerial Systems (UASs) adopted are radio and GPS-controlled small aircraft or multicopters that show significant potential for aerial data acquisition (Colomina and Molina 2014). Photogrammetry is a widely used methodology for creating digital elevation models (DEMs) and orthorectified image mosaics from aerial (stereo) photographs (Lillesand 2006).

Recent developments in image processing have rapidly increased the popularity of UASs. In particular Structure-from-Motion (SfM) and MultiView Stereo (MVS) algorithms have proved very successful for the 3D reconstruction of surfaces and landscapes (Westoby et al. 2012; Vericat et al. 2014). SfM/MVS is able to process thousands of (GPS-tagged) images automatically, without the use of Ground Control Points (GCPs) and manual georeferencing, producing very dense point clouds, digital surface models (DSMs) and orthorectified photomosaics at centimeter scale (Westoby et al. 2012; Harwin and Lucieer 2012).

In addition to the high spatial resolution, UAS can be utilized anytime to produce high temporal resolution data. In particular fixed-wing systems can cover relatively large areas and so image entire catchments. This enables analysis of small-scale processes at catchment scales (Colomina and Molina 2014). In this sense, UAS can provide data products for geomorphological analysis with enough detail in both the spatial and temporal domain. Recent studies have proven the value of UAS in various research disciplines, for example very-high resolution topographic modeling in natural (Mancini et al. 2013) and rural environments (Mancini et al. 2013) or riverine (Watanabe and Kawahara 2016), for purposes of e.g. geomorphological mapping (Hugenholtz et al. 2013), studying soil surface characteristics (Corbane et al. 2012) or analyzing processes such as landslide dynamics (Lucieer et al. 2014; Stumpf et al. 2013), soil and gully erosion (Marzolff et al. 2011; D’Oleire-Oltmanns et al. 2012), and rangeland monitoring (Laliberte et al. 2010).

Despite the fact that many researchers are already applying UAS in their work, there is little known about the accuracy of UAV protocols and image data products. Harwin and Lucieer (2012) indicate that SfM/MVS point clouds can reach sub-decimeter accuracy whilst, James and Robson (2012) note centimeter precision at 50 m altitude. Furthermore, Gindraux et al. (2017) studied the influence of GCPs in the DSMs accuracy over eight surveys (made with multi-rotor platform) distributed on three glaciers in the Swiss Alps. The authors found that the DSMs accuracy diminish rate of 0.09 meters per 100-meters distance, and achieved minimum horizontal and vertical accuracy from 0.1 and 0.03 meters. Finally, Forlani et al. (2018) assessed the DSMs accuracy from a fixed-wing UAV with a on-board Real-time kinematic (RTK) in a urban scenario. The experiments show that using the RTK system proposed does not improve vertical and horizontal accuracy. Using 12 GCP the accuracy worst case is about 2 and 3.3 cm, while with RTK it decreases to average values from 2.4 cm (horizontal) and 4.6 cm (vertical). The authors suggest that this result might be due to a system misconfiguration.

Nevertheless, how accuracy changes with relief and flight strategy was not studied before. Flight lines are created based on the take-off location and direction. The actual flight altitude varies significantly throughout a survey, particularly when changes of relief are within the same order of magnitude as the flight altitude, which is often the case when using low-altitude aerial photography in medium – high relief environments. With different flight directions there will be a variable spatial distribution of flight altitude which may result in different DSM reconstructions. Moreover, camera properties, motion blur caused by internal (platform) or external (weather) factors, camera angle, and illumination conditions all affect image quality which in turn may affect surface reconstructions and the generation of orthophotos (O’Connor et al. 2017). For monitoring campaigns it is crucial to understand and minimize such variation and so avoid misrepresentation of “change” captured by multi-temporal data sets.

Within this context, the goal of this paper is to investigate how DSM (and orthophoto) accuracy varies with different flight strategies and if there is a noticeable trade-off between spatial resolution and aerial surveying time. In the medium-relief and semi-arid region of Murcia, Spain, several multiple flights, with different mission parameters, such as, flying altitude and area coverage orientation were undertook. The paper concludes with a discussion on the usability of UAS for monitoring geomorphological change and vegetation development.

Methods

Study area

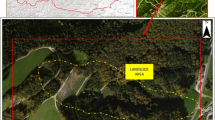
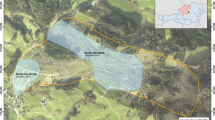
The field site is located in the semi-arid Lorca basin, in Southeastern Spain where the Luchena river joins the northern branch of the Puentes reservoir (37^∘45’20.62”N, 1^∘51’19.99”W). Due to the dry conditions (270 mm annual rainfall, potential evapotranspiration > 900 mm) this area has only limited and partial vegetation cover which allows reconstruction of the actual ground surface (see Fig. 1) (Sanchez-Toribio et al. 2010). The site is a small denudation niche developed in a Holocene to late Pleistocene lacustrine terrace with gypseferous and calcareous lacustrine silts, comparable to the terraces as described in (Baartman et al. 2011). This denudation niche is re-shaped by man-made, almost level, bench terraces which now show extreme forms of gullying, piping and collapsed pipes. These terraces were abandoned around 2000 after cultivation with drip irrigated crops. Some physical and chemical characteristics of the site’s top soil can be found in van der Meulen et al. (2006).

Fig. 1

a The study area is located in the Province of Murcia in southeastern Spain. The photos represent the study area, including the damaged check dams (b), and the UAS (c)

Erosion features in this region have been a topic of interest for a long time. Both long-term erosion (Ruiz-Sinoga and Diaz 2010) and contemporary erosion processes (García-Ruiz et al. 2013; Nadeu et al. 2015) have been under study. Erosion features in natural areas (Díaz and Bermúdez 1988; Martínez-Hernández et al. 2017; Díaz et al. 2007) and in cultivated areas (Romero-Díaz et al. 2017; de-las Heras et al. 2019) have been studied. In addition, much focus has been put on potential measures to prevent erosion in cultivated areas; both in dryland as well as in irrigated areas (Castillo et al. 2007; Calatrava et al. 2011; García-Ruiz et al. 2013; Hooke and Sandercock 2017).

Materials and software

The flights were carried out using a MAVinci Sirius 1 UAS, which is a typical low-weight ready-to-fly system, and the methodology and output that are described in this paper can be considered representative for other contemporary UAS. Ground speed is approximately 50 km/h during flights with low wind speed, with the maximum flight time ranging between 30-60 minutes. The carrying capacity is approximately 0.5 kg with a GPS and inertial measurement unit (IMU). A Panasonic Lumix GX1 16 megapixel camera, which can collect both RAW and JPEG photos (at 0.5 and 1.5 frames per second) was used. In this study only JPEG format images were collected.

Flight planning was carried out with the MAVinci Desktop that is part of the MAVinci UAS. Images were processed with Structure-from-Motion photogrammetry (with Agisoft Photoscan Pro 1.0 software) and further analysis carried out with Python 2.7 and the Geospatial Data Abstraction Layer (GDAL).

Ground control points (GCPs)

Without the use of GCPs the horizontal and vertical accuracy of products derived from the aerial imagery (point cloud, digital elevation models, orthorectified imagery) is similar to the accuracy of the GPS device on board of the UAS, which is in the range of several meters. By re-aligning the SfM point cloud (more info in Section “Flight procedure”) with a limited number of accurate GCPs this accuracy can be improved significantly (Turner et al. 2012), up to several centimeter accuracy.

In total 15 GCPs have been positioned strategically, i.e. well distributed throughout the area to capture the outer regions of the area of interest, as well as the lowest and highest points of the area of interest. Moreover, GCPs have been placed near special areas, such as important breaks-of-slope of the terrace levels near gully systems of interest). The GCPs themselves were simple 80 cm x 80 cm orange textile rectangles, with in the center a black textile square containing a CD disk. The centers of the CD disks were measured with a TOPCON Hiper Pro DGPS (Differential Global Positioning System) that has a horizontal and vertical accuracy of 10 mm. The orange textile combined with the CD made it easy to recognize the GCPs from the aerial imagery and find the exact point of measurement.

Flight procedure

Flight lines were created based on a selected area of interest and a desired Ground Sampling Distance (GSD). The higher the flight altitude (i.e. distance to ground surface), the larger the GSD. A single flight line is constant in heading and elevation (distance to mean sea level) to ensure a stable flight, however, elevation can vary between flight lines to match the landscape’s topography and minimize variations of GSD throughout the data set. Flight lines and camera trigger locations enabled 85% overlap in flight direction and 65% sidelap. After landing, the GPS/ENU logs were copied to the EXIF metadata of the images.

SfM/MVS processing chain

The aerial imagery was processed using Structure-from-Motion (SfM) and MultiView Stereo algorithms (MVS) as implemented in the commercially available software Agisoft Photoscan Professional (v1.0) (AgiSoft 2014). There are freely available alternatives such as VisualSfM V0.5.24 (Wu 2013), Microsoft PhotoSynth for the creation of SfM/MVS point clouds, which then need further processing in software such as ArcGIS V10.6 (commercial) or Meshlab (free). The SfM/MVS processing chain is summarized in Fig. 2.

Fig. 2

Schematic overview of the processing chain in Agisoft Photoscan. The flow chart differentiates input data, processing steps and output data. The numbers correspond to the steps in Section “Flight procedure”

In general, the processing steps are: 1) Import selected imagery. Selection criteria can be based on camera orientation (roll/pitch/yaw) or blurriness to ensure the processing of high-quality, in-focus, images. We selected imagery with a maximum roll and pitch of 10 degrees; 2) Camera alignment and estimation of interior camera parameters. This step uses the SfM algorithm which is developed specifically for creating 3D models of unstructured photo collections (Brown and Lowe 2005). SfM requires multiple images of an object from different camera positions, where possible with > 70% overlap. Image features are identified in image pairs and used as tie points for 3D reconstruction. The output is a unfiltered point cloud which has an approximate average point spacing of 0.5-1 m (Rosnell and Honkavaara 2012); 3) Manual identification and placement of GCPs in the imagery data; 4) Optimization of interior camera parameters and georeferencing of the sparse point cloud to best fit the GCP coordinates; 5) Generation of a dense point cloud using MVS. MVS revisits the SfM image pairs, reduces noise and generates more points between the tie points (Seitz et al. 2006). Typically for UAS data, the average point cloud spacing is approximately 0.05 m, depending on flight altitude, camera specifications and surface properties; 6) The dense point cloud is used to create a continuous mesh which can be converted to a DSM; and 7) Texture is blended on top of the mesh to create an orthorectified image mosaic of the aerial photos.

Experimental design

Data acquisition

In a single day we undertook three flights over the study area. The flights were labeled based on their direction (A-B) and relative altitude (1-3). The first flight had flight lines in a north-south (N-S) direction at a relatively low altitude (A1), the second flight had flight lines in a southwest-northeast (SW-NE) direction at a medium altitude (B2), and third flight had flight lines in a SW-NE direction at a relatively high altitude (B3).

In order to compare camera altitude and flight direction independently, additional data sets were created. High-resolution images were resampled to a lower resolution in order to replicate higher altitude flights. The images from flight A1 were resampled to match the GSD of higher altitudes 2 and 3, creating the image sets A2* and A3*. Images from flight B2 were resampled to B3* to match the same GSD as flight B3 to see the impact of differences in UAV stability during a flight. For clarity the * indicates the data set has been resampled, instead of original flight imagery. Camera altitude was calculated based on the on-board GPS-measured aircraft elevation and the produced DSM of flight B3:

$$ Alt_{A1} = Alt_{A1} - Z_{DSM} $$

(1)

$$ Alt_{B2} = Alt_{B2} - Z_{DSM} $$

(2)

where Alt_A1 is the camera altitude (above ground surface), Z_A1 is the camera elevation (above mean sea level) and Z_DSM is the ground surface elevation. The DSM of flight B3 was selected because this flight had the largest coverage. The ratio of mean camera altitude between A1 and B2 was used to calculate the target GSD of A2*:

$$ R = \frac{\overline{Alt_{A1}}}{\overline{Alt_{B2}}} $$

(3)

$$ GSD_{A2*} = GSD_{A1}.R $$

(4)

where R is the ratio of mean flight altitude of A1 and B2. Here the mean camera altitudes, rather than individual values, were used to preserve the standard deviation of altitude and replicate the increase in elevation for the entire set of flight lines as a whole. The same principle was used to create data sets A3* (based on A1) and B3* (based on B2). The images were resampled (linear interpolation) within the freely available NConvert image processor.¹

New camera elevations of the resampled images were calculated based on the DSM and (mean) camera elevations:

$$ Z_{A2*} = Z_{A1*} - \overline{Alt_{A1}} + \overline{Alt_{B2}} $$

(5)

where $\overline {Alt_{A1}}$ and $\overline {Alt_{B2}}$ are mean camera altitudes of A1 and B2 respectively. These values were stored in the EXIF metadata of the JPEG images for further processing. The same procedure was carried between flight A1 and flight B3 to create the resampled image set A3*. In this way we acquired two data sets with varying GSD in flight direction A and three data sets with varying GSD in flight direction B. See Table 1 for an overview of the analyzed data sets.

Table 1 Overview of the data sets created. Heading A/B refers to direction of the flight lines, i.e. NS and SW – NE, respectively. Altitude 1-3 refers to three mean altitude zones, and F/R refers to “Flight” and “Resampled data set”

Tests

The six data sets were used to create and compare the constructed DSMs and orthophotos. The tests focused on: The cell size of the data products, vertical and horizontal accuracy, absolute difference of DSMs, the spatial distribution of deviation between different flight sets, and registration of recognizable features. The cell size of the data products is automatically determined in Agisoft Photoscan based on the average point spacing of the dense point cloud. Moreover, the overall vertical accuracy of the DSM is determined by using absolute vertical deviation from the dGPS measurements,

$$ A_{v} = \frac{\sum\limits_{i=1}^{n} |Z_{DSM_{i}} - Z_{dGPS_{i}}|}{n} $$

(6)

where A_v is the average vertical accuracy of the DSM, Z_DSM and Z_dGPS are the z-values from the DSM and dGPS, respectively, and n is the number of validation GCPs. For the horizontal accuracy of the orthophoto, manual digitization of marker locations in the orthophoto were compared with the dGPS measurements of the marker locations. Similar to the vertical accuracy calculations, average deviation from the dGPS measurements was used as a basis to assess the horizontal accuracy of the orthophoto,

$$ A_{h} = \frac{\sum\limits_{i=1}^{n} |XY_{Ortho_{i}} - XY_{dGPS_{i}}|}{n} $$

(7)

where A_h is the overall horizontal accuracy, XY_ortho is the (x,y) position of the GCP in the orthomosaic, XY_dGPS is the (x,y) position of the GCP as measured by the dGPS, and n is the number of validation GCPs.

Furthermore, the absolute difference of DSMs and the spatial distribution of deviation between different flight sets gives insight in to the reproducibility of the process chain and usability for topographic change detection or landscape monitoring. Preparation of the original data sets was required to match the grid systems (location of grid cell center and cell size) of two DSMs. We used the highest resolution data set as the target grid system, and used GDAL’s reprojection tool to resample the second data set into the same grid system. Subsequently grid cells of the DSMs were subtracted for comparison. Finally, the registration of recognizable features in the data products includes geomorphological entities, such as rills and gullies, and surface objects such as vegetation and infrastructure.

Results

Data acquisition

Table 2 shows a summary of the data characteristics of the acquired imagery and derived products. The three flights A1, B2 and B3 took approximately 40, 30 and 20 minutes, respectively, covering 55 – 96 hectares. Average flight altitude was 126, 153 and 235 m, with a standard deviation of 10 – 11 m. The number of images varied from 1458 in flight A1 to 524 in B3. The A2*, A3* and B3* image sets have similar properties.

Table 2 Overview of the data product characteristics with regard to the data introduce in Section “Data acquisition”: Flight direction (P1), Average altitude (P2), Std. altitude (P3), Appr. flight altitude (P4), # of images (P5), Area coverage (P6), Average point spacing (P7), Average point density (P8), DSM cell size (P9), Orthophoto cell size (P10), MAE ± Std. DSM (P11), MAE ± Std. orthophoto (P12), Precision ratio DSM (P13), and Precision ratio orthophoto (P14)

Figure 3 shows the camera elevation [meters above sea level] and altitude [meters above ground surface] of the imagery of the six data sets. The two flight directions are clearly visible (N-S for A1-3; SW-NE for B2-3), with the distance between flight lines and camera locations decreasing with lower altitude. This is due to the smaller footprint (field of view) of the camera at lower altitudes. The elevation within a flight line is constant, but between flight lines elevation varies to minimize variation of the average GSD in the hilly landscape. Nevertheless, there’s considerable variation of camera altitude (Fig. 3-bottom) and the related GSD. It is expected this variation results in a non-uniform spatial distribution of error in elevation of the DSM, and detail in the orthophoto.

Fig. 3

The subsets show the locations (in UTM Zone 30N coordinates in [m]), elevation [m] and altitude [m] of the aircraft and the camera

Test results

The following section presents the results from the comparisons, concerning cell size, vertical and horizontal accuracy, difference of DSMs, and registration of recognizable features. A DSM and orthophoto from the study area is depicted in Fig. 4.

Fig. 4

Example of the DSM (Digital Surface Model), and shaded relief with 50% transparency (left) and the orthophoto (right), produced with images from flight A1. The colored dots represent the locations of the GCPs and vertical and horizontal deviation from dGPS measurements

Cell size

The cell size of the derived DSM and orthophoto is listed in Table 2, and is related to the average flight altitude and GSD. A higher flight altitude results in a larger GSD in the imagery, resulting in fewer identifiable features and so a larger point spacing. The cell size of the DSM is approximately equal to the point spacing of the dense point cloud; the cell size of the orthophoto is approximately equal to the average GSD. With the current set up, DSMs and orthophotos with cell sizes of 4.7 – 9.0 cm and 2.4 – 4.5 cm respectively were constructed, which potentially provides enough detail for fine-scale topographic and geomorphological analysis and vegetation studies and classifications, up to single vegetation units.

Vertical and horizontal accuracy

Figure 5 shows the vertical and horizontal deviation from dGPS measurements, which are summarized in Table 2 by the mean absolute error (MAE) and standard deviation. The same GCPs were used to calculate the MAE, and therefore represent the model fit. MAE is hereafter referred to as vertical and horizontal error. With images from flight A1 we were able to produce a DSM with a vertical error of less than five centimeters. With increasing altitude, the vertical error increases in sets A2* and A3*. For flights B2-3 with flight direction SW-NE the vertical error does not increase as much.

Fig. 5

Absolute vertical deviation [m] with dGPS at different flight altitudes

The horizontal error appears stable with different flight directions and altitudes and was consistently lower than 5 cm, i.e. not more than 1-2 pixels.

Difference of DSMs

We assume that the variability in output found are a result of differences in data acquisition or processing. For example, variability of output can be caused by: 1) topography, which we assumed to be stable since all flights were carried out on the same day. Topography also affects relative flight altitude and associated GSD; 2) weather, which influences air and ground speed, turbulence, and light conditions, which can lead to differences in motion blur and texture in the images; and 3) flight lines, including altitude and orientation (roll, pitch and yaw). Figure 6 shows the Difference of DSMs (DoDs) which present the distribution of variation when different DSMs are subtracted from each other. Here, the DSM noted on the left label is subtracted from the DSM noted in the label at the top. Several noteworthy differences can be seen.

• 1. In areas with high vegetation such as trees and high shrubs, DoDs show high differences, for example in the southwest corner. In such areas, small variation or error in xy leads to high variation in z.

• 2. B3 versus B3* represents two flights with the same elevation and the same direction, and should ideally produce similar results. In general, the difference between both DSMs is 5-10 cm and corresponds to the vertical deviation to the dGPS measurements presented in Fig. 5. Moreover, several “bumps” and “depressions” are located in the center of the DoD.

• 3. A1 versus A2* and A3*, A2* versus A3*, and B2 versus B3 show the effect of flight altitude. In general, flights at different altitudes are found to generate comparable DSMs within 5-10 cm variation. Yet, flights at higher altitudes appear to estimate lower areas slightly higher, and the higher areas lower; flights at higher altitude are more ‘flattened’.

• 4. B2 versus B3, which are actual flights rather than resampled imagery, show higher variations than when comparing B2 versus B3* that share the same source imagery.

• 5. A2* versus B2, and A3* versus B3 show the impact of flight direction. Generally flight direction has a much stronger impact on the elevation values than flight altitude. In the center higher elevation values, up to 15-20 cm difference, are calculated with flights in the B direction compared to flights in the A direction. Also, the lower area in the southwest is modeled with higher elevation values in the B flights.

Fig. 6

Subsets showing difference of DSMs [m] of the different flights. The labels at the left and top show which DSMs were compared. The colors from blue to red represent -0.2 to 0.2 meters difference. The location of the subset is shown by the black rectangle in Fig. 4. For clarity the * indicates the data set has been resampled, instead of original flight imagery (please refer to Section “Data acquisition”)

Registration of recognizable features

Figure 7 shows the DSMs of a terraced and abandoned agricultural field that is damaged by gully erosion initiated by piping processes, captured during flights A1 – B3. Despite more detail in the DSMs at the lower altitude flights, it is evident that in all flights the same processes and landforms can be clearly recognized, i.e. the extensive gully in the center, parallel small gully systems, and piping channels exiting along the edge of the terrace (e.g. in the lower left in the subset). The irregular patterns around the gullies are vegetation patches and small shrubs. With lower resolution images from higher altitude flights more vegetation points are filtered out, resulting in a relatively smooth DSM in areas with vegetation. All this features have been identified and labeled by a technician.

Fig. 7

Subsets showing the DSMs of a terraced abandoned agricultural field that is incised by different gully systems. The blue and red color represent 469 - 473 m elevation. The black lines show the location of the cross section presented in Fig. 8. The outline of the subset is highlighted by the blue rectangle in Fig. 4

The variation in vertical accuracy of the DSM in Fig. 5 is reflected in the cross section profiles shown in Fig. 8. Flight A1 shows the most detail, including higher values of vegetation height. The depth of the gully channel varies depending on the flights, particularly A3*. While the mean flight altitude of B3 and A3* is the same, the spatial distribution of flight altitude is different.

Fig. 8

Cross section of two gully channels extracted from the DSMs from the different flights

Figure 9 shows the different orthophotos produced by the different sets of imagery. It is evident that lower altitude flights produce a more detailed orthorectified mosaic, and detail is gradually reduced with increasing altitude. Nevertheless, even in the A3* and B3 sets, individual shrubs and trees can be recognized. This means that for most vegetation mapping or monitoring campaigns higher altitude flights are likely to produce sufficient detail. In addition, there are not significant visual differences noted between orthophotos produced with the two different flight directions.

Fig. 9

Subsets showing the orthophotos produced with the different flight imagery. The outline of the subset is highlighted by the red rectangle in Fig. 4. For clarity the * indicates the data set has been resampled, instead of original flight imagery (please refer to Section “Data acquisition”)

Discussion

This section discusses how the reproducibility of flight campaigns can be maximized for different purposes, such as mapping, measuring, and monitoring the geomorphological or ecological state of a landscape.

Impact of flight strategy on DSMs and orthophotos

In general, higher altitude flights produce images with larger grid cells which is expected. With larger grid cells only larger features can be identified, resulting in fewer tie points and fewer points in the final dense point cloud. A sparser point spacing leads to a DSM with larger grid cells. Not only does the size of the grid cells increase, but the detail of the DSM also decreases due to the point filtering algorithm that is part of the multiview stereo processing. For example, flight A1 shows most detail in the DSM (Fig. 6) and the derived profile in Fig. 8. The ‘bumps’ in the A1 profile at the left edge of the left channel, and the right edge of the right channel, are shrubs. In higher altitude flights parts of the vegetation (e.g. branches) have few tie points, which are then considered noise and removed. Lower altitude imagery produces more tie points for (parts of) the vegetation which are not considered noise. The result is a more irregular shaped DSM including vegetation heights with lower altitude flights, and a smoother DSM where vegetation is partly removed with higher altitude flights. This effect has to be taken into account in studies where vegetation height is relevant.

Vertical and horizontal errors

The order of magnitude of absolute vertical errors in this study (Fig. 5) are in line with recent literature (e.g. (Lucieer et al. 2014; Mancini et al. 2013) and are within an acceptable range (5 – 10 cm) for many applications. Distinct morphological change can be measured, but subtle topographic variation will not be detected within the operating limitations of an aircraft. Flights with direction A showed a noticeable decrease of vertical accuracy with increasing altitude, but flights with direction B did not show any decrease in accuracy. This may indicate the B direction flight lines are more optimal, but this has to be tested further. Moreover, studies that used hand-held or close-range SfM photogrammetry note a vertical accuracy of less than 2.5 cm (e.g. (Gómez-Gutiérrez et al. 2014)). The higher vertical errors from this study are a result of greater altitude, lack of oblique images, low cost camera and/or higher relief (Rossi et al. 2017). Multicopters could potentially produce more accurate DEMs as they are able to fly at lower altitudes, and often have a larger payload for more advanced cameras, but at the cost of area coverage (Colomina and Molina 2014).

Differences on DSMs

The DoDs values (Fig. 7) are also of the same order of magnitude as presented by e.g. (Westoby et al. 2012). In the northeast and southwest higher values are found, which are caused by insufficient overlap of imagery and an absence of GCPs in that area. Higher flight altitudes appears to flatten the DSM in a way that the lowest areas in the southwest are slightly higher and higher areas in the northeast are slightly lower. This effect could be important to studies focusing on erosion and deposition of soil material, particularly if single hillslopes are photographed. In addition, comparisons of DSMs B2, B3 and B3* show several ‘bumps’ that represent locally higher and lower areas. Because they are not present in the B2/B3* comparison, these bumps are not likely the effect of flight altitude, but are possibly the result of different weather conditions during the flight and instability of the aircraft caused by wind turbulence.

Gully-level analysis

The channel profiles in Fig. 8 show good similarities between the location and shape of the gully channels. In mapping campaigns, this means that results are not affected by different flight strategies and results are reproducible. On the other hand, the depth of the gully channel is calculated differently in each flight, particularly A3*. The offset of A3* compared to B3 in the profile is possibly the effect of locally higher flight altitude causing larger image grid cells and less points in the generated point cloud. Here, points resembling the channel bottom may be absent, or are in too few number and considered noise and so filtered out. Such variation in reconstructed channel depths will affect volumetric calculations and therefore care is strongly advised when UAS data is used to estimate erosion rates in such systems.

Area coverage orientation

The cell size and level of detail in the DSMs was not affected by flight direction, and geomorphological features are equally well represented in the surface models. With different flight directions mean flight altitude remains the same, and therefore also the GSD and the number of points in the point clouds. On the other hand, the DoDs show considerable variation in DSM elevation between two different flight directions and it appears that flight direction has much more impact on elevation values than flight altitude. For example, A2* versus B2, and A3* versus B3 in Fig. 6 represent the differences of DSMs flown at similar mean altitude, but with a different flight direction. Particularly in the center of the area higher, there are elevation values with up to 15-20 cm difference. The elevation differences between DSMs with different flight direction are considerably larger than those caused by, presumably, wind conditions as depicted by DoDs between B3 and B3*. Therefore, a consistent flight direction should be considered when planning multi-temporal flight campaigns.

The question remains whether there is an optimal flight direction. Some authors have proposed approaches to reduce the effective flying time (Girardet et al. 2014), i.e. this is the time that the UAV takes from take-off, to landing, and to increase the energy-efficiency of the platform (Rodriguez et al. 2016). In this approach the authors take advantage of headwinds to minimize flight time. Other authors (Coombes et al. 2018) argue that flying perpendicular to the wind allows faster time-to-destination times to be achieved. To the best of the authors knowledge there is not a clear investigation about the effect of wind and flight direction on area coverage. However, the literature suggests that an online path planning approach that takes in consideration of the wind direction, shears, and gusts, would compensate attitude losses and drifts during the flight (Rodriguez et al. 2016).

Comparison with other sensors

When compared to multi-temporal airborne laser altimetry data, similar issues occur. Here different point cloud densities or reflections at different locations result in different surface models and inaccuracies due to filtering and interpolation (Anders et al. 2013). With UAV imagery now much easier and cheaper to acquire and the difference in error for most flight scenarios for DTM production less than 10 cm, they are a good choice for many applications. Nevertheless, if decimeter vertical accuracy is important, then independent secondary measurements are crucial to ensure the quality of a UAV DSM. To some extent, the elevation differences we found may be attributed to systematic error due to radial distortion of the camera described by (James and Robson 2012); incorporating oblique images and cross flights may reduce this error. Combining images from different altitudes may also reduce vertical errors.

Labelling and classification

In all flights performed, the orthophoto provided enough detail for the identification of individual vegetation patches which could be used as input for classifications or vegetation distribution studies (Laliberte et al. 2010).

Conclusions

This paper has demonstrated the impact of flight altitude and direction on the quality of surface models and orthophotos derived from low altitude aerial photography with a UAS. Three flight altitudes and two different flight path orientations were tested. It was shown that UAS data products clearly capture detailed morphology and vegetation structure. While the vertical accuracy of DSMs does not clearly differ with increasing flight altitude, elevation values are sensitive to different flight path orientations. It was also shown that horizontal accuracy and the lateral positioning of features in the orthophotos does not change with different flight altitudes and directions. The results suggest that SfM/MVS with UAS imagery is suitable for mapping geomorphological features and vegetation distribution, but for monitoring topographic or geomorphological change special care is required to optimize and repeat the same flight paths at each stage.