Abstract
Floods are among the most devastating natural hazards in the world, affecting more people and causing more property damage than any other natural phenomena. One of the important problems associated with flood monitoring is a flood extent extraction from satellite imagery, since it is impractical to acquire the flood area through field observations. This paper presents a new method to the flood extent extraction from synthetic-aperture radar (SAR) images that is based on intelligent computations. In particular, we apply artificial neural networks, self-organizing Kohonen’s maps (SOMs), for SAR image segmentation and classification. We implemented our approach in a Grid system that was used to process data from three different satellite sensors: ERS-2/SAR during the flooding on the river Tisza, Ukraine and Hungary (2001), ENVISAT/ASAR WSM (Wide Swath Mode) and RADARSAT-1 during the flooding on the river Huaihe, China (2007).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Increasing numbers of natural disasters have demonstrated to the mankind the paramount importance of the natural hazards topic for the protection of the environment, and the citizens. Climate change is likely to increase the intensity of rainstorms, river floods, and other extreme weather events. The dramatic floods of Central and Eastern Europe in summer 2002 and spring 2001 and 2006 emphasize the extreme in climatic variations. Floods are among the most devastating natural hazards in the world, affecting more people and causing more property damage than any other natural phenomena (Wood 2001). That is why, the problems of flood monitoring and flood risk assessment are among priority tasks in national satellite monitoring systems and the international Global Earth Observation System of Systems (GEOSS; Work Plan 2007–2009 defined by the international Group on Earth Observation—GEO (2007)).
Efficient monitoring and prediction of floods and risk management is impossible without the use of Earth Observation (EO) data from space. Satellite observations enable acquisition of data for large and hard-to-reach territories, as well as continuous measurements. One of the most important problems associated with a flood monitoring is a flood extent extraction, since it is impractical to determine the flood area through field observations. The flood extent is very important for calibration and validation of hydraulic models to reconstruct what happened during the flood and determine what caused the water to go where it did (Horritt 2006). The flood extent can be also used for damage assessment and risk management, and can benefit to rescuers during flooding (Corbley 1999).
The use of optical imagery for flood monitoring is limited by severe weather conditions, in particular presence of clouds. In turn, SAR (synthetic aperture radar) measurements from space are independent of daytime and weather conditions and can provide valuable information to monitoring of flood events. This is mainly due to the fact that smooth water surface provides no return to antenna in microwave spectrum and appears black in SAR imagery (Elachi 1988; Rees 2001). In contrast, a wind-ruffled surface can give backscatter larger than that of the surrounding land. This, in turn, considerably complicates the detection of water surfaces on SAR images for flood applications. Though such surfaces are not present in our data sets, we plan to investigate the influence of the wind on water detection from SAR imagery in the future works.
As a rule, flood extent extraction procedure from SAR imagery consists of the following steps. The first step is to re-construct a satellite image taking into account the calibration, the terrain distortion using digital elevation model (DEM) and providing exact geographical coordinates. The second step is to provide partition of the image into regions that have the same characteristics (segmentation). And the third step consists in the classification to determine the flood extent.
This paper proposes to use artificial neural networks (NN), in particular self-organizing Kohonen’s maps (SOMs; Haykin 1999; Kohonen 1995), for SAR image segmentation, and the further classification. SOMs provide effective software tool for the visualization of high-dimensional data, automatically discover of statistically salient features of pattern vectors in data set, and can find clusters in training data pattern space which can be used to classify new patterns (Kohonen 1995). We applied our approach to the processing of data acquired from three different satellites: ERS-2/SAR during the flooding on the river Tisza, Ukraine and Hungary, 2001, ENVISAT/ASAR WSM (Wide Swath Mode), and RADARSAT-1 during the flooding on the river Huaihe, China, 2007.
As to software implementation of our approach, we should take into account the following considerations: (1) the need to fuse data from various sources: optical (without clouds) and SAR imagery, DEM, land cover/use, etc.; (2) the need for creation of image mosaics with the aim to analyze large territories; (3) the need for processing in the near real-time for fast response within international programs and initiatives for disaster monitoring, in particular the International Charter “Space and Major Disasters” and the International Federation of Red Cross. All these factors, as well as the need for managing large volumes of satellite data, lead to the use of Grid technologies (Foster 2002; Fusco et al. 2003, 2007; Shelestov et al. 2006). This paper will also highlight issues regarding the creation of an InterGrid infrastructure that integrates resources of the Space Research Institute NASU-NSAU, the Institute of Cybernetics NASU and the China’s Remote Sensing Satellite Ground Station of CAS (RSGS-CAS).
Existing approaches to flood extent extraction
To this end, different methods were proposed to flood extent extraction from satellite imagery. In the European Space Agency (ESA), a multi-temporal technique is applied to the flood extent extraction from SAR images (ESA Earth Watch, http://earth.esa.int/ew/floods). This technique uses SAR images of the same area taken on different dates (one image is acquired during flooding and the second one in “normal” conditions). The resulting multi-temporal image clearly reveals change in the Earth’s surface by the presence of colour in the image. This method has been implemented in ESA’s Grid Processing on Demand (G-POD, http://eogrid.esrin.esa.int).
Cunjian et al. (2001) applied threshold segmentation algorithm to flood extent extraction from RADARSAT-1 imagery with the support of digital topographic data. Firstly, RADARSAT SAR imagery was filtered by Enhanced Frost filter (Frost et al. 1982) with window size of 7 × 7 pixels, and geo-registered to the topographic map. Secondly, flood extent was primarily extracted from RADARSAT SAR imagery using threshold segmentation. Thirdly, DEM was created from the digital topographic data by using GIS software. Fourthly, simulated SAR imagery was created from DEM. Finally, the simulated SAR imagery was registered to RADARSAT SAR imagery, and the shade from the simulated SAR image was used to mask the mislabeled flood extent from RADARSAT SAR due to its shadow influence. The drawback of this approach is that threshold value should be chosen manually, and will be specific for different SAR instruments and images.
Csornai et al. (2004) used ESA’s ERS-2 SAR images and optical data (Landsat TM, IRS WIFS/LISS, NOAA AVHRR) for flood monitoring in Hungary in 2001. To derive flood extent from SAR imagery, change detection technique is applied. This technique uses two images made before and during the flood event, and some “index” that reveals changes in two images and, thus, the presence of water due to the flooding (Wang 2002).
Though these methods are rather simple and fast (in computational terms), they possess some disadvantages: they need manual threshold selection and image segmentation, require expertise in visual interpretation of SAR images and require the use of complex models for speckle reduction; spatial connections between pixels are not concerned.
More sophisticated approaches have been proposed to segment SAR imagery for flood and coastal applications.
Horrit (1999) has developed a statistical active contour model for segmenting synthetic aperture radar (SAR) images into regions of homogeneous speckle statistics. The technique measures both the local tone and texture along the contour so that no smoothing across segment boundaries occurs. A smooth contour is favoured by the inclusion of a curvature constraint, whose weight is determined analytically by considering the model energy balance. The algorithm spawns smaller snakes to represent multiply connected regions. The algorithm was tested to segment real SAR imagery from ESA’s ERS-1 satellite. The proposed approach was capable of segmenting noisy SAR imagery whilst accurately depicting (to within 1 pixel) segment boundaries. But application of active contour algorithm, in general, is subject to certain difficulties such as getting stuck in local minima, poor modelling of long concavities, and producing inaccurate results when the initial contour is chosen simple or far from the object boundary (Shah-Hosseini and Safabakhsh 2003). For statistical active contour models, one should also have a priori knowledge of image statistical properties. In a case of real SAR imagery, statistics may be badly represented by a modelled distribution. Moreover, spatial correlation and regions of smoothly varying statistics may also occur (Horrit 1999).
In an approach proposed by Niedermeier et al. (2000), an edge-detection method is first applied to SAR images to detect all edges above a certain threshold. A blocktracing algorithm then determines the boundary area between land and water. A refinement is then achieved by local edge selection in the coastal area and by propagation along wavelet scales. Finally, the refined edge segments are joined by an active-contour algorithm. In this case, the error is estimated by comparing the results achieved with a model based on visual inspection: the mean offset between the final edge and the model solution is estimated to be 2.5 pixels (Niedermeier et al. 2000). But the number of the parameters and threshold values affecting processing robustness is considerable in this approach.
Dellepiane et al. (2004) have proposed an innovative algorithm being able to discriminate water and land areas in order to extract semi-automatically the coastline by means of remote sensed SAR images. This approach is based on fuzzy connectivity concepts and takes into account the coherence measure extracted from an InSAR (Interferometric Synthetic Aperture Radar) couple. The method combines uniformity features and the averaged image that represents a simple way of facing textural characteristics. One major disadvantage of this method is that we should have two precisely co-registered SAR images in order to estimate InSAR coherence measure.
Martinez and Le Toan (2007) used a time series of 21 SAR images from L-band PALSAR instrument onboard JERS-1 satellite to map the flood temporal dynamics and the spatial distribution of vegetation over a large Amazonian floodplain. The mapping method is based on decision rules over two decision variables: (1) the mean backscatter coefficient computed over the whole time series; (2) the total change computed using an “Absolute Change” estimator. The first variable provides classification into rough vegetation types while the second variable yields a direct estimate of the intensity of change that is related to flood dynamics. The classifier is first applied to the whole time series to map the maximum and minimum flood extent by defining three flood conditions: never flooded (NF); occasionally flooded (OF); permanently flooded (PF). Then, the classifier is run iteratively on the OF pixels to monitor flood stages during which the occasionally flooded areas get submerged. The mapping accuracy is assessed on one intermediate flood stage, showing a precision in excess of 90%. But to achieve this precision, the proposed classifier should be built on more than eight images (Martinez and Le Toan 2007).
In this paper, we propose a neural network approach to flood extent extraction from satellite SAR imagery. Our approach is based on segmentation of a single SAR image using self-organizing Kohonen maps (SOMs) and further image classification using auxiliary information on water bodies derived from Landsat-7/ETM+ images and Corine Land Cover (for European countries).
Data sets description
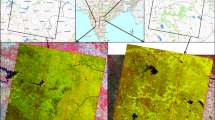
We applied our approach to the processing of remote-sensing data acquired from three different satellites: ERS-2 (flooding on the river Tisza on March 2001—see Fig. 1), ENVISAT and RADARSAT-1 (flooding on the river Huaihe on July 2007—see Fig. 2). Data from European satellites were provided from ESA Category-1 project “Wide Area Grid Testbed for Flood Monitoring using Spaceborne SAR and Optical Data” (No. 4181). Data from RADARSAT-1 satellite were provided from RSGS-CAS.
Flooding (a, date of acquisition is 10.03.2001) and post-flooding (b, 14.04.2001) SAR/ERS-2 images of the river Tisza. Rectangle on top image indicates areas shown in Fig. 4a (© ESA 2001)
A pixel size and ground resolution of ERS-2 imagery (in ENVISAT format, SLC—Single Look Complex) were 4 and 8 m, respectively; for ENVISAT imagery—75 and 150 m; and for RADARSAT-1 imagery—12.5 and 25 m.
For more precise geocoding of SAR images (in particular, ERS-2 images) and validation of obtained results, we used the following set of auxiliary data: Landsat-7/ETM+, European Corine Land Cover (CLC 2000) and SRTM DEM (version 2).
Neural network is built for each SAR instrument separately. In order to train and test neural networks, we manually selected the ground-truth pixels with the use of auxiliary data sets that correspond to both territories with the presence of water (we denote them as belonging to a class “Water”) and without water (class “No water”). The number of the ground-truth pixels for each of the image is presented in Table 1.
For each image, these data were randomly divided into the training set (which constituted 75% of total amount) and the testing set (25%). Data from the training set were used to train the neural networks, and data from the testing set were used to verify the generalization ability of the neural networks, i.e. the ability to operate on independent, previously unseen data sets (Haykin 1999).
Among the selected ground-truth pixels we have not used those that relate to the boundaries between water and no water lands. Classification of SAR images on more than two classes (e.g. “Water”, “No water”, different levels of water and vegetation presence) is beyond the scope of this paper and will be investigated in future papers.
Neural network method for flood extent extraction from SAR imagery
Our method for flood extent extraction consists of the data pre-processing, image segmentation and classification on two classes using self-organising Kohonen maps (SOMs). These steps are as follows:
-
1.
Transformation of raw data to lat/long projection. Level-1 data from ERS-2 and ENVISAT satellites in Envisat format and from RADARSAT-1 satellite in CEOS format were provided with ground control points (GCPs) inside the files that were used to transform images to lat/long projection in GeoTIFF format. For this purpose, we used gdalwarp utility from GDAL (Geospatial Data Abstraction Library, http://www.gdal.org).
-
2.
Image calibration. In order to calibrate ERS-2/SAR and ENVISAT/ASAR images, we used standard procedures described in (Laur et al. 2004) and (Rosich and Meadows 2004), respectively. As a result of image calibration, the output signal (pixel values) was transformed to backscatter coefficient (in dB). For RADARSAT-1 image, we used original pixel values in DN (digital number).
-
3.
Geocoding. We made additional geocoding procedure for the ERS-2 image in order to improve the accuracy. This was performed manually in RSI Envi software with the use of Landsat/ETM + and CLC2000 data.
-
4.
Orthorectification of the SAR images is performed using a procedure described in (Cossu et al. 2007).
-
5.
Image processing using self-organizing Kohonen’s maps (SOMs). SOM is a type of artificial neural network that is trained using unsupervised learning to produce a low-dimensional (typically two dimensional), discretised representation of the input space of the training samples, called a map (Haykin 1999; Kohonen 1995). The map seeks to preserve the topological properties of the input space. SOM is formed of the neurons located on a regular, usually one- or two-dimensional grid. Neurons compete with each other in order to pass to the excited state. The output of the map is a, so called, neuron-winner or best-matching unit (BMU) whose weight vector has the greatest similarity with the input sample x.
The network is trained in the following way: weight vectors w j from the topological neighbourhood of BMU vector i are updated according to (Haykin 1999; Kohonen 1995)
where η is learning rate (see Eq. 3), h j,i (x)(n) is a neighbourhood kernel around the winner unit i, x is an input vector, \(\left\| \cdot \right\|\) means Euclidean metric, L is a number of neurons in the output grid, n denotes a number of iteration in the learning phase.
The neighbourhood kernel function h j,i( x ) (n) is taken to be the Gaussian
where r j i (x) are the vectorial locations in the display grid of the SOM, σ(n) corresponds to the width of the neighborhood function, which is decreasing monotonically with the regression steps.
For learning rate we used the following expression:
where τ is a constant. The initial value of 0.1 for learning rate was found experimentally.
Kohonen maps are widely applied to the image processing, in particular image segmentation and classification (Haykin 1999). Prior neural network training, we need to select image features that will be give to the input of neural network. For this purpose, one can choose original pixel values, various filters, Fourier transformation etc (Gonzalez and Woods 2002). In our approach we use a moving window with backscatter coefficient values for ERS-2 and ENVISAT images and DNs for RADARSAT-1 image as inputs to neural network. The output of neural network, i.e. neuron-winner, corresponds to the central pixel of moving window (see Fig. 3).
In order to choose appropriate size of the moving window for each satellite sensor, we ran experiments for the following windows size: 3 × 3, 5 × 5, 7 × 7, 9 × 9 and 11 × 11.
We, first, used SOM to segment each SAR image where each pixel of the output image was assigned a number of the neuron in the map. Then, we used pixels from the training set to assign each neuron one of two classes (“Water” or “No water”) using the following rule. For each neuron, we calculated a number of pixels from the training set that activated this neuron. If maximum number of these pixels belonged to class “Water”, then this neuron was assigned “Water” class. If maximum number of these pixels belonged to class “No water”, then this neuron was assigned “No water” class. If neuron was activated by neither of the training pixels, then it was assigned “No data” class.
For neural network quality assessment, we used two parameters:
-
Quantization error that is estimated using the following expression
$$QE = \frac{1}{N}\sum\limits_{t = 1}^N {\left\| {{\mathbf{x}}_t - {\mathbf{w}}_{i\left( {{\mathbf{x}}_t } \right)} } \right\|} ,\,\,\,\,\,i\left( {{\mathbf{x}}_t } \right) = \arg \mathop {\min }\limits_{j = \overline {1,L} } \left\| {{\mathbf{x}}_t - {\mathbf{w}}_j } \right\|{\text{,}}$$
where N is the number of the pixels.
-
Classification rate that shows relative number of correctly classified pixels from the training and testing sets.
Results of image processing
In order to choose the best neural network architecture, we ran experiments for each image varying the following parameters:
-
size of the moving window for images that define the number of neurons in the input layer of the neural network;
-
number of neurons in the output layer, i.e. the sizes of two-dimensional output grid.
Other parameters that were used during the image processing are as follows:
-
neighbourhood topology: hexagonal;
-
neighbourhood kernel around the winner unit: the Gaussian function (see Eq. 2);
-
initial learning rate: 0.1;
-
number of the training epochs: 20.
The initial values for the weight vectors are selected as a regular array of vectorial values that lie on the subspace spanned by the eigenvectors corresponding to the two largest principal components of the input data (Kohonen 1995). Using this procedure, computation of the SOM can be made orders of magnitude faster, since (1) the SOM is then already approximately organized in the beginning, (2) one can start with a narrower neighbourhood function and smaller learning rate.
The results of experiments for the images are presented in Table 2.
For the images with higher spatial resolution (i.e. ERS-2 and RADARSAT-1), the best results were achieved for larger moving window 7 × 7. In turn, for the ENVISAT/ASAR WSM image, we used the moving window of smaller size 3 × 3. The use of higher dimension of input window for the ENVISAT image led to the coarser resolution of the resulting flood extent image and reduced classification rate. The resulting flood extent images for ERS-2, ENVISAT and RADARSAT-1 satellites are shown in Figs. 4, 5 and 6.
For comparison we also computed the flood extent using threshold segmentation algorithm. For each SAR image, threshold values were chosen manually in order to maximize the classification rate for the testing sets (see Table 3).
The resulting flood extent images derived using the threshold segmentation are shown in Fig. 7.
From Table 3 and Fig. 7 we can see that for ENVISAT image threshold algorithm gave rather good results. While for the ERS-2 and RADARSAT-1 images, this algorithm fails to produce precise flood extent. But, again, the threshold algorithm requires manual selection and adjustment of the threshold values that precludes use of the algorithm in automated mode.
Implementation in Grid infrastructure
Regarding implementation of our approach, we should take into account the following considerations:
-
1.
The need to integrate multi-source data. For example, we had to use both ENVISAT and RADARSAT-1 imagery in order to derive integrated information on flood extent for the River Huiahe, China. Neither of these two images covered the whole basin of the river;
-
2.
The need for the creation of image mosaics. When analysing large territories, we need to complement SAR-derived flood extent with information from high-resolution optical imagery. This requires the creation of mosaics from dozens of images which is a time consuming task, and effective management of large volumes of satellite data;
-
3.
Security issues regarding satellite data policy;
-
4.
The need for processing in the near real-time for fast response within international programs and initiatives for disaster monitoring, in particular the International Charter “Space and Major Disasters” and the International Federation of Red Cross.
All these factors, as well as the need for managing large volumes of satellite data, lead to the use of Grid technologies (Foster 2002; Fusco et al. 2003, 2007; Shelestov et al. 2006). In this case, a Grid environment is considered not only for providing high-performance computations, but, in fact, can facilitate interactions between different actors by providing a standard infrastructure and a collaborative framework to share data, algorithms, storage resources, and processing capabilities (Fusco et al. 2007).
We developed a parallel version of our method for flood extent extraction that can be run on several computational nodes. Parallelization of the image processing is performed in the following way: SAR image is split into the uniform parts that are processed on different nodes using the OpenMP Application Program Interface (www.openmp.org). We deployed this method in the InterGrid infrastructure that integrates resources of geographically distributed organisations, in particular:
-
Space Research Institute NASU-NSAU (Ukraine) with deployed computational and storage nodes based on Globus Toolkit 4 (htpp://www.globus.org) and gLite 3 (http://glite.web.cern.ch) middleware, access to geospatial data and Grid portal;
-
Institute of Cybernetics of NASU (Ukraine) with deployed computational and storage nodes based Globus Toolkit 4 middleware and access to computational resources (approximately 500 processors);
-
RSGS-CAS (China) with deployed computational nodes based on gLite 3 middleware and access to geospatial data (approximately 16 processors).
It is also worth mentioning that satellite data are distributed through the InterGrid environment. ENVISAT WSM data are stored on ESA’s rolling archive and routinely downloaded for the Ukrainian territory. Then, they are stored in the Space Research Institute archive that is accessible via the InterGrid. For other territories, ENVISAT data are acquired on demand. RADARSAT-1 data are stored on RSGS-CAS site.
The use of the Grids allowed us to considerably reduce the time required for image processing. In particular, it took approximately 10 min to process a single SAR image on a single workstation. The use of Grid computing resources allowed us to reduce the time to less than 1 min.
Access to the resources of the InterGrid environment is organised via a high-level Grid portal that have been deployed using GridSphere framework (Novotny et al. 2004). Through the portal, users can access the required satellite data and submit jobs to the computing resources of the InterGrid in order to process satellite imagery. The workflow of the SAR image processing steps in the Grid (such as transformation, calibration, orthorectification, segmentation and classification) is controlled by a Karajan engine (http://www.gridworkflow.org/snips/gridworkflow/space/Karajan).
The existing architecture of the InterGrid is shown in Fig. 8.
In order to visualize the results of image processing in the InterGrid environment, we use an OpenLayers framework (http://www.openlayers.org) and UNM Mapserver v5. UNM Mapserver supports the Open Geospatial Consortium (OGC) Web Map Service (WMS) standard that enables the creation and display of registered and superimposed map-like views of information that come simultaneously from multiple remote and heterogeneous sources (Beaujardiere 2006).
The developed services for flood monitoring provide access to the basic geospatial data VMap0 that is acquired automatically via Internet using OGC WMS standard, raw SAR imagery, and the derived flood extent. For each region, we also created mosaics from optical Landsat-7/ETM+. These services are accessible via Internet by address http://floods.ikd.kiev.ua/. The examples of the screenshots for the Ukrainian and Chinese case-study areas are shown in Figs. 9 and 10.
Conclusions
In this paper we proposed a neural network approach to flood extent extraction from SAR imagery. To segment and classify SAR image, we applied self-organizing Kohonen’s maps (SOMs) that possess such useful properties as ability to automatically discover statistically salient features of pattern vectors in data set, and to find clusters in training data pattern space which can be used to classify new patterns. As inputs to neuron network, we used a moving window of image pixels intensities. We ran experiments to choose the best neuron network architecture for each satellite sensor: for ERS-2 and RADARSAT-1 the size of input was 7 × 7 and for ENVISAT/ASAR the moving window was 3 × 3. The advantages of our approach are as follows: (1) we apply moving window to process the image and thus considering spatial connection between pixels; (2) neural network’s weight vectors are adjusted automatically by using training data; (3) to determine flood extent, we need to process a single SAR image. This enables implementation of our approach in automatic services for flood monitoring. Considering the selection of ground-truth pixels to calibrate the neuron network, i.e. to assign each neuron one of the classes (“Water” and “No water”), this process can be also automated using geo-referenced information on water bodies for the given region. We applied our approach to determine flood extent from SAR images acquired by three different sensors: ERS-2/SAR for the river Tisza, Ukraine; ENVISAT/ASAR and RADARSAT-1 for the river Huaihe, China. Classification rates for independent testing data sets were 85.40%, 98.52% and 95.99%, respectively. These results demonstrate the efficiency of our approach.
We developed a parallel version of our method and deployed it in the InterGrid infrastructure that integrates computational and storage resources of the geographically distributed organisations: the Space Research Institute NASU-NSAU, the Institute of Cybernetics NASU and the China’s Remote Sensing Satellite Ground Station of CAS. The use of Grid technologies is motivated by the need to make computations in the near real-time for fast response to natural disasters and to manage large volumes of satellite data. Currently, we are using a Grid portal solution based on GridSphere framework to integrate Grid systems with different middleware, such as GT4 and gLite 3. In the future we plan to implement a metascheduler approach based on a GridWay-like system.
References
Beaujardiere J (2006) OpenGIS® web map service implementation specification. Open Geospatial Consortium, Atlanta
Corbley KP (1999) Radar Imagery Proves Valuable in Managing and Analyzing Floods Red River flood demonstrates operational capabilities. Earth Observation Magazine, vol. 8, num. 10. Accessible via http://www.eomonline.com/Common/Archives/1999dec/99dec_corbley.html. Accessed 16 Apr 2008
Cossu R, Brito F, Fusco L, Goncalves P, Lavalle M (2007) Global automatic orthorectification of ASAR products in ESRIN GPOD. 2007 ESA ENVISAT Symposium, Montreux Switzerland, 23–27 April 2007
Csornai G, Suba Zs, Nádor G, László I, Csekő Á, Wirnhardt Cs, Tikász L, Martinovich L (2004) Evaluation of a remote sensing based regional flood/waterlog and drought monitoring model utilising multi-source satellite data set including ENVISAT data. In: Proc. of the 2004 ENVISAT & ERS Symposium (Salzburg, Austria, 6–10 September 2004)
Cunjian Y, Yiming W, Siyuan W, Zengxiang Z, Shifeng H (2001) Extracting the flood extent from satellite SAR image with the support of topographic data. Proc of Int Conf on Inf Tech and Inf Networks (ICII 2001) 1:87–92
Dellepiane S, De Laurentiis R, Giordano F (2004) Coastline extraction from SAR images and a method for the evaluation of the coastline precision. Pattern Recogn Lett 25:1461–1470
Elachi C (1988) Spaceborne radar remote sensing: applications and techniques. IEEE, New York
Foster I (2002) The grid: a new infrastructure for 21st century science. Phys Today 55(2):42–47
Frost V, Stiles J, Shanmugan K, Holtzman J (1982) A model for radar images and its application to adaptive digital filtering of multiplicative noise. IEEE Trans Pattern Anal Machine Intell 4(2):157–165
Fusco L, Goncalves P, Linford J, Fulcoli M, Terracina A, D’Acunzo G (2003) Putting Earth-Observation Applications on the Grid. ESA Bulletin 114:86–90
Fusco L, Cossu R, Retscher C (2007) Open grid services for envisat and earth observation applications. Plaza AJ, Chang C-I. High performance computing in remote sensing Taylor & Francis Group, New York 237–280
GEO (2007) GEO Work Plan. Toward Convergence. Available via www.earthobservations.org/documents/wp0709_v4.pdf. Accessed 16 Apr 2008
Gonzalez RC, Woods RE (2002) Digital Image Processing. Prentice Hall, Upper Saddle River
Haykin S (1999) Neural networks: a comprehensive foundation. Prentice Hall, Upper Saddle River
Horritt MS (1999) A statistical active contour model for SAR image segmentation. Image Vis Comput 17:213–224
Horritt MS (2006) A methodology for the validation of uncertain flood inundation models. J Hydrology 326:153–165
Kohonen T (1995) Self-organizing maps. Series in information sciences 30. Springer, Heidelberg
Laur H, Bally P, Meadows P, Sanchez J, Schaettler B, Lopinto E, Esteban D (2004) ERS SAR Calibration. Derivation of the Backscattering Coefficient in ESA ERS SAR PRI Products. ES-TN-RS-PM-HL09 05, November 2004, Issue 2, Rev. 5f
Martinez JM, Le Toan T (2007) Mapping of flood dynamics and spatial distribution of vegetation in the Amazon floodplain using multitemporal SAR data. Remote Sens Environ 108:209–223
Niedermeier A, Romaneeßen E, Lenher S (2000) Detection of coastline in SAR images using wavelet methods. IEEE Trans Geosci Remote Sens 38(5):2270–2281
Novotny J, Russell M, Wehrens O (2004) GridSphere: An Advanced Portal Framework. In: 30th EUROMICRO Conference, pp 412–419
Rees WG (2001) Physical principles of remote sensing. Cambridge University Press, Cambridge
Rosich B, Meadows P (2004) Absolute calibration of ASAR level 1 products generated with PF-ASAR. ESA-ESRIN, ENVI-CLVL-EOPG-TN-03-0010, 07 October 2004
Shah-Hosseini H, Safabakhsh R (2003) A TASOM-based algorithm for active contour modelling. Pattern Recogn Lett 24:1361–1373
Shelestov A, Kussul N, Skakun S (2006) Grid technologies in monitoring systems based on satellite data. J Automation and Inf Sci 38(3):69–80
Wang Y (2002) Mapping extent of floods: what we have learned and how we can do better. Natural Hazards Rev 3(2):68–73
Wood HM (2001) The Use of Earth Observing Satellites for Hazard Support: Assessments & Scenarios. Final Report. National Oceanic & Atmospheric Administration, Dept of Commerce, USA. Available via http://www.ceos.org/pages/DMSG/2001Ceos/overview.html. Accessed 16 Apr 2008
Acknowledgements
This work is supported by ESA CAT-1 project “Wide Area Grid Testbed for Flood Monitoring using Spaceborne SAR and Optical Data” (No. 4181) and by joint project of INTAS, the Centre National d’Etudes Spatiales (CNES) and the National Space Agency of Ukraine (NSAU), “Data Fusion Grid Infrastructure” (Ref. Nr 06-1000024-9154).
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by: H. A. Babaie
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License ( https://creativecommons.org/licenses/by-nc/2.0 ), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Kussul, N., Shelestov, A. & Skakun, S. Grid system for flood extent extraction from satellite images. Earth Sci Inform 1, 105–117 (2008). https://doi.org/10.1007/s12145-008-0014-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12145-008-0014-3