Introduction

Connections are everywhere – internet interactions, spreading of diseases, travel connections, economic transactions and personal/professional/social relationships – and now they have a specific label: Networks. Today, the application of networks to cognitive neuroscience has become increasingly popular and revolutionized the way in which the architecture of brain is conceived (Sporns, 2011). This revolution is both theoretical and pragmatic. From a theoretical point of view, neural networks mechanism can be operationalized as ‘a set of interactions amongst large-scale neural populations (e.g. cortical regions) that take part in an explanation of a cognitive phenomenon. The underlying view thus advocates that cognition is the result of coordinate and collective processes, dynamics and interactions unfolding within a complex network (Bressler & Menon, 2010; Sporns, 2011). Pragmatically, there is a growing body of communities that are developing databases containing information spanning from neural measures to behavioral ones. One of the most prominent examples is the Human Connectome Project (HCP), a large-scale initiative that promotes the characterization of human brain connectivity linking it to cognition and to behavioral disorders (Van Essen et al., 2012) and implements huge datasets that include wealth of cognitive, personality and psychopathology measures along with measures of socio-economic status, general health and demographics.

Despite this new “connectome era”, the variety of individual facets or domains – e.g., cognition, personality, mental health, social and emotional functioning – are typically studied as separate watertight compartments. This is particularly surprising if we consider the fact that they are all phenomena linked to the same entity: the human brain. Plenty of theories indeed grew up within the investigation field of each one of these domains (but not among) with the purpose of delineating a picture of their organization.

In the cognitive domain, a well-established theory in cognitive science is the g-factor theory (Spearman, 1904), which postulates the existence of a single factor that explains a large amount of variance (~ 45–50%) across test scores from many different cognitive domains (Austin et al., 2002; Floyd et al., 2009). Indeed, the fact that scores among cognitive tests show positive correlations is often claimed to support the idea of the g factor. Furthermore, the g factor has been shown powerful to predict significant life outcomes (Barrett & Depinet, 1991), such as educational achievement (Deary et al., 2007), income, occupational status and success (Jensen, 1980; Schmidt & Hunter, 2004; Strenze, 2006). On the other hand, the Multiple-Factor Theories posit that the cognitive realm cannot be explained by one single factor. Some examples of them are the theory of fluid and crystallized intelligence (Cattell, 1987; Horn, 1965; Horn & Cattell, 1998) or the theory of multiple intelligences, first proposed by Gardner (2000). The problem with multiple-factor theories is that even if it is possible to assume that more than one factor could better fit the vast majority of data, nevertheless, there is no a proper rule as to the number of factors that should emerge from a matrix (Stankov, 2005) of measures.

In the personality domain, the focus has been directed on several “group” factors, as the Big Five personality traits. The Big Five model claims that neuroticism, extraversion, openness, agreeableness and conscientiousness are the major factors of personality (Costa & McCrae, 1992). This model has been empirically derived, and it has been replicated in many cultures and across adults of all ages (McCrae & Costa, 2003). Furthermore, these personality traits have been demonstrated to predict outcomes in several areas such as subjective physical health, well-being, and longevity (Ozer & Benet-Martínez, 2005). The six-domainal framework (the HEXACO model) included another factor called Honesty–Humility defined by traits such as modesty and sincerity versus deceit, greed and conceit (Hahn et al., 1999). Shortly after the introduction of this new model of personality structure, the “Dark Triad” of Narcissism, Machiavellianism and Psychopathy has been developed to better delineate individual’s characteristics underrepresented in five-domainal models (Paulhus & Williams, 2002). More recently, however, it has been proposed a general factor of personality, which holds that individual differences in personality can be accounted for by one overarching factor that aggregates the common variance in personality traits as the Big Five (Musek, 2007).

Such ‘clustering’ approaches have received renewed interest also in stratifying psychiatric disorders, with the aim to identify more consistent subgroups on the basis of data derived from many sources of information (Marquand et al., 2016). Although it emerged a general interest and attention among researchers in the attempt to domainalize and cluster the specific individual abilities/traits into broader factors and concepts, a general shift from splitting to lumping has been observed not only in cognitive neuroscience but also in cognitive and personality psychology and psychopathology.

Yet, so far, no frameworks have been developed to shape a comprehensive overview of possible reciprocal interactions amongst the distinct characteristics that form the human mind and to domainalize them. Most of the studies trying to reduce this gap, indeed, focused on studying specific personality-cognition-psychopathology relationships, with several and, often, opposite results and visions. Originally, previous reviews of relationships between personality and intelligence concluded that, with some exceptions, personality and intelligence are not related (Brebner & Stough, 1995; Hofstee, 2001). This exception was represented by Openness to experience: Individuals high in openness have, on average, higher levels of intelligence (Hofstee, 2001; Wolf & Ackerman, 2005). Successive studies did find many personality–cognition relationships, drawing however a mixing puzzle of results (Lounsbury et al., 2005; Osmon et al., 2018; Soubelet & Salthouse, 2011; Wolf & Ackerman, 2005). The most consistent finding remains however that higher levels of Openness are related with better performance on several cognitive tests (Soubelet & Salthouse, 2011). Likewise, the exploration of cognitive and personality profiles in psychopathology mostly focused on single, separate, relationships, such as the study of intelligence in schizophrenia (Khandaker et al., 2011), or neuroticism in anxiety and depression disorders (Weinstock & Whisman, 2006).

The difficulties underlying this lack of a comprehensive model of connections among human facets are comprehensible. Gathering data ranging from cognitive to psychopathological measures through behavioral and demographical ones can be extremely high-demanding for both single researches and reviews. Moreover, once data are available, identifying a flexible methodology to analyze them is not a trivial issue. Inside this last aspect, nonetheless, promising approaches can be found, such as network analysis.

Given a network structure, it is possible to observe which nodes are the most central, namely those nodes that are the most connected to others or have a central role in the flow of information. Furthermore, it is possible to detect how the nodes can define specific communities/clusters, intended as network sections in which a set of nodes are connected each other (Chandrasekaran et al., 2010; Golino & Demetriou, 2017). An approach that allows estimating a network and subsequently identifying its clusters is called Exploratory Graph Analysis (Golino & Epskamp, 2017). EGA has been applied to model animal behavior (Martin et al., 2019), to detect some political domains (Hopp, 2019) and psychological features (Bell & O’Driscoll, 2018).

A network defined by EGA represents a model of both the bidirectional relations among different variables and the domains they define due to their conceptual connections. Such model, even if providing a considerable amount of new information, has a non-trivial limitation: it is undirected (McNally et al., 2017). In other words, these models inform us only about the presence of a partial correlation among variables or clusters, reducing the chance of false or spurious relations among them. The possibility that such models could be more complex, namely that they could contain also causal relationships among nodes or clusters, needs to be explored. A well-established approach to study such complex models is the Bayesian Network (BN) approach (Scutari et al., 2017). BNs enable to both identify and study causal paths among nodes of a network, information that cannot be otherwise detectable by using the aforementioned network models (Briganti et al., 2020). As suggested by the authors, the concept of causality should be read with caution. In the present paper, BNs are used to detect a directed connection of a node toward another one and not the opposite.

All the described procedures represent innovative approaches to analyze and understand several kinds of data. Nonetheless, they have been always applied either separately or with purposes away from defining an architecture among human domains.

In the present study, we took advance of these approach to provide an architecture of the connections among human domains. In particular, we applied both EGA and BN on a set of 38 target measures extracted from the HCP database (Van Essen et al., 2012) (~ 1200 subjects) to accomplish three main aims:

  • starting from the associations among variables, identifying high-order domains that explain the individual variability in human cognition and behavior;

  • characterizing the architecture of the relationships among such domains;

  • unveiling possible direct influences among domains.

Addressing these goals led to the formulation of a statistically-based and data-driven framework of human behavior and mental activity and structure.

Materials and methods

Sample. A publicly available database – the Human Connectome Project (HCP) – was used in this study (http://www.humanconnectomeproject.org/). The HCP consisted of 1206 individuals (656 female and 55 male subjects). The age ranged from 22 to 37 years old (M = 28.84; SD = 3.69). Inclusion and exclusion criteria are reported in Table S1. Consent to participate and Ethical approval are not applicable to this study since already collected data (i.e., the HCP data) were analyzed.

Measures. The HCP database represents the first large-scale project to collect and freely share data to build a map of the functional and structural neural connections of the adult human brain. Although this is the primary aim of the HCP, nonimaging measures were also collected since such information is important to understand the relationship between brain connectivity and behavior. Nonimaging measures comprise:

  • Demographics (e.g., Education, Employment, income).

  • Physical and mental health history.

  • Present and past use of tobacco, alcohol, marijuana, and other drugs.

  • Symptoms/history of: Eating disorders, depression, psychosis, anti-social personality, obsessive-compulsive disorder, post-traumatic stress, social phobia, panic attach.

  • Folstein MiniMental State Exam.

  • Pittsburgh Sleep Quality Index.

  • Parental Psychiatric and neurologic history.

  • Handendness assessment.

  • Menstrual cycle and other endocrine information in females.

  • Urine drug assessment, breathalyzer test, Blood test.

  • NIH Toolbox behavioural tests (which includes 19 subdomains within the broad domains of cognitive, motor, emotional and sensory functions; see Barch et al., 2013).

  • Non-NIH Toolbox behavioural tests (color vision, contrast sensitivity, personality, attention, episodic memory, fluid intelligence, emotion processing, spatial processing, and delay discounting).

The full list of imaging and nonimaging measures of the database with a detailed description can be visible here at the following link: https://wiki.humanconnectome.org/display/PublicData/HCP-YA+Data+Dictionary-+Updated+for+the+1200+Subject+Release.

In line with studies (Cona et al., 2019; Smith et al., 2015), we selected 38 measures from the HCP database, reflecting cognitive and processing aspects, mental health and behavioral problems, personality characteristics, and substance use frequencies. We used a similar approach of the studies by Smith et al. (2015) and Cona et al. (2019), thus the selection criteria for measures inclusion were:

  • Variables related to mental health, mental disorders, and personality.

  • Variables related to cognitive skills or constructs evaluated by the HCP developers, not self-reported ones.

  • Variables related to behavioral disorders or addictions.

Moreover, we also applied the following exclusion criteria:

  • We excluded all those measure that were sub-components of high-order variables. For instance, we excluded the items assessing the specific sleep problems, since a total score of sleep quality was provided.

  • We excluded variables that were highly correlated with more major related variables but not assessing specific constructs. For instance, among the measures assessing internalizing/externalizing disorders, we excluded the “Other problems” score.

  • We excluded redundant measures or similar ones. For instance, we preferred to keep a score for the depressive symptomatology instead the number of depressive symptoms.

  • We excluded variables with too low values/measurements across the subjects.

  • We excluded variables with no variance across subjects.

Table S2 in Supplementary Materials shows the original name of each variable, the assessment tool from it belongs to, a brief description, the name label assumed in the results, the observed mean, standard deviation, and the range.

Exploratory Graph Analysis. As mentioned within the Introduction, the Exploratory Graph Analysis (EGA) is an approach allowing to both define a network model and estimate its communities/ clusters. EGA showed to have some formal advantages on procedures commonly used to estimate latent domains such as parallel analysis (Horn, 1965) or minimum average partial procedure (Schwarz, 1978). In particular, these procedures may underestimate the number of latent domains in cases of small sample sizes, high correlations among latent domains or few variables per factor (Crawford et al., 2010; Keith et al., 2016). EGA seems to be unaffected by such situations (Golino & Epskamp, 2017). Moreover, EGA has a practical advantage, namely the possibility of detecting the number of latent domains and defining which item/observed variable belongs to each domain, within the same analysis. Such advantages are particularly relevant when the aim of the model tested is a network models instead of a factor one (Christensen & Golino, 2021). To understand if the data we used were more prone to be described by network model than a factor one, we applied the Loadings Comparison Test resampling our data 200 times (Christensen & Golino, 2021). The results of such a test suggested us that the data were closer to a network model with a proportion of 99% of times. Moreover, we checked whether the data were circular: according to Brandenburg and Papenberg (2022), EGA is less accurate when applied to circular data and, consequently, to circumplex models. We performed this check by using the circular package (Agostinelli & Lund, 2022). Data emerged as non-circular.

The EGA algorithm (Golino & Epskamp, 2017) is described below.

The first step consists of estimating the network model, namely a Gaussian graphical model where the nodes are the variables of interest and edges correspond to partial correlation coefficients of two variables conditioned on all other variables. A zero-coefficients denotes conditional independence between two variables. This approach, nonetheless, could lead to large standard errors and possible model’s overfitting, since the high number of possible associations could lead to false positives. To minimize such possibility, it is possible to estimate the model by using the least absolute shrinkage and selection operation (Epskamp et al., 2018), a penalized maximum likelihood estimation that fixes weak associations to zero and enhances the estimation of an interpretable network with a parsimonious set of connections. When the network is estimated, EGA applies a walktrap community detection algorithm to estimate the number of clusters/communities. Briefly, such algorithm finds similar nodes based on random walks over the network’s edges, searching for densely connected sections of such network. Once the clusters are found, the nodes composing it are graphically coded and can be displayed with the same color (Christensen & Golino, 2019). For each cluster, it is possible to examine also the network loadings of each item/variable to its cluster. Network loadings are a measure of the association of a node to a specific cluster that is based on the node strength (i.e., the sum of the connection values of a node) and it can be compared to the factor loadings of the CFA when a factor model is estimated (Christensen, Golino, et al., 2019). Accordingly with the guidelines by Christensen and Golino (2021), network loadings ≤ 0.15 can reflect a small node association with their communities; values between 0.15 and 0.25 a moderate association and ≥ 0.35 could reflect a large association.

In the present study, we estimated an initial Gaussian Graphical model where the nodes where the measures selected from the HCP database and the edges corresponded to partial correlation coefficients of two variables conditioned on all other variables. We used the GLASSO algorithm to define the partial correlations. We set the tuning parameter γ necessary to control the sparsity of the resulting network was set to 0.5. We used the walktrap algorithm(Pons & Latapy, 2005) instead of to the triangulated maximally filtered graph (Massara et al., 2017). We applied a cross-validation logic in order to both test and validate the network model. Therefore, we split the data: we randomly extracted from the total set of 1206 participants a former subsample of 663 participants to estimate the exploratory network model (i.e., the 55% of the sample). This sample size was coherent with other studies using such technique (Bell & O’Driscoll, 2018; Christensen, Gross, et al., 2019; Golino & Epskamp, 2017). We used data relative to the remaining 543 individuals of the original database to validate the network model through a confirmatory analysis. We applied the Weighted Least Squares estimator with robust standard errors and a mean- and variance adjusted test statistic (WLSMV), since some variables were not normally distributed. Therefore, we examined the goodness indices of fit of the found network (and its clusters division). We adopted the Comparative Fit Index (CFI ≥ 0.95 representing a good fit, while CFI ≥ 0.9 for an adequate fit), the Root Mean Square Error of Approximation’s (RMSEA ≤ 0.05 indicating a good fit, and a RMSEA between 0.5 and 0.8 an adequate fit) and the Standardized Root Mean Square Residual (SRMR ≤ 0.08 representing a good fit). To avoid results dependent on the sample specificity, we applied also a non-parametric bootstrap (4000 replications), which resampled with replacement the data contained within the original dataset and estimated, for each replication, an EGA network. We then compared the results obtained from the first EGA with the median network (and its clusters) obtained by bootstrap. We checked the stability of the first network, calculated as the proportion of times the original network was found among the replications (assuming that the original network coincided with the median one). Furthermore, we used the bootstrapped results to observe if and how many times an item/variable is associated to its domain, across replications. It is conceptually similar to what is done for a bootstrapped confirmatory factor analysis. Whenever an item/variable overcomes an a priori defined threshold (usually 0.80) of node strength, it is considered as stable and can be identified in its domain consistently (Christensen & Golino, 2019). On the contrary, items/variable whose node strength was under the threshold or that were equally associated to different domain could be considered problematic and potentially removable (Christensen & Golino, 2019). In the present study, we used the threshold of 0.80.

After the network definition and the communities’ identification, we calculated the following centrality indices: the strength of a node (or degree for unweighted networks), namely the sum of all the (absolute) edges values linked to such node; the betweenness, a measure reflecting how many times a node lies on the shortest path between two other nodes of the network; the closeness, an index representing how much a node is closer to all other nodes (Dalege et al., 2017). We used the qgraph package(Epskamp et al., 2012) and the EGAnet package (Golino & Christensen, 2019) within R environment (R Core Team, 2020).

Bayesian Network approach. In order to explore possible causal paths among nodes of the emerged network model, we adopted the BN approach (Scutari et al., 2017). Given a set of variables X, a BN is a statistical model that allows to define the probabilistic and causal relationship among the variables Xi ∈ X through a directed acyclic (i.e., without loops) graph (DAG). In such graph, the nodes are the variables Xi ∈ X and the edges are direct stochastic dependences, which decompose the global probability distribution of X into a set of local probability distributions of each node Xi, as showed by the following equation (Scutari et al., 2017):

$$p\left(\varvec{X}\right)= \prod _{i=1}^{N}p\left({X}_{i}\right|Pa\left({X}_{i}\right))$$

where \(p\left(\varvec{X}\right)\) is the global probability distribution of X, \(N\) is the number of the nodes Xi ∈ X (in the present study \(N=38\)), \(p\left({X}_{i}\right|Pa\left({X}_{i}\right))\) is local probability distributions of each node Xi, and \(Pa\left({X}_{i}\right)\) are all the nodes whose arcs (i.e., the edges) are directed toward Xi. For mathematical demonstrations, see Scutari and Denis (2014). As a result, the network will be composed of nodes and of arrows describing the direction of the dependence among nodes, intended as causal paths (Briganti et al., 2020). On the causality issue, it is important to stress that the causal path is not to be strictly intended as an exhaustive cause-effect relationship, but a putative causal path in which a specific node may influence another node, but not the opposite. They give us an idea of a potential causal model underlying our data. There are no assumptions of temporal dependence of a variable on another (Jones et al., 2018). This is particularly valid in case of cross-sectional or observational studies (McNally et al., 2017). To estimate a BN, a double-step procedure is required.

The first step is called structure learning and aims at “learning” (an expression inherited from machine learning) the arcs of the network. It is similar to the model selection for regression analysis, where adding or removing a node and its arcs (a regressor in terms of linear models) changes the posterior probability distribution of the network. Such probability is estimated with the Bayesian Information Criterion (Scutari et al., 2017). As for the regression models, BNs should be defined under some basic assumptions (Scutari & Denis, 2014). For instance, each node should be normally distributed and there should not be latent variables acting as confounding factor (Scutari & Denis, 2014).

In BNs approach, it is possible to encode prior knowledge about the connections among nodes, through the so called whitelisted and blacklisted arcs: the former is a set of arcs that must be included in the final BN, forcing the learning algorithm to create them; the latter set refers to arcs that must not appear in the final BN, forcing the learning algorithm to exclude their definition (Scutari & Denis, 2014).

Once the data and the sets of a priori arcs are defined, it can be selected a structure learning algorithm to estimate the BN. Once the algorithm is selected, it is possible to learn the structure. This operation can be done by estimating a single model from data (i.e., executing a learning algorithm once). As pointed out by Scutari et al. (2017), this approach could not account for the uncertainty inside such unique statistical solution. Another solution is to learn the BN toward a model averaging approach. It is a technique frequently used to learn a BN and consists of re-sampling the data using a bootstrap procedure. At each replication a BN is defined, and its arcs are temporarily stored. Once all the replications are performed, two parameters are used to define the final BN: the former is called arc strength, namely the percentage of time that an arc is present regardless its direction; the latter is called arc direction, that is the percentage of times that an arc presented a specific direction, across the replications (Scutari et al., 2017).

The second step of the procedure aimed at defining and testing a BN consists in the so-called parameter learning. Generally, it consists in estimating the aforementioned local distributions of each node from the graph defined by the first step of the procedure. In terms of regression models (typical of Gaussian Bayesian Networks that handles continuous data), it consists in calculating the regression coefficient of each node against the nodes connected to it (i.e., its parents). In other words, each node becomes the response variable, while the parent nodes the predictors. In this way, it is possible to quantify the putative causal influence of a node on another node. This second step is frequently used to make inferences or to simply answer to some questions or issues found in scientific literature on the topic of interest (Scutari et al., 2017). In the following lines, we describe the steps we made to define the BN.

In the present study, we firstly addressed the assumption regarding the communities intended as latent variables. This step was crucial to build the BN. In the previous section, we defined communities reflecting latent domains. To avoid that such latent domain would result as confounding variables, we estimated a score for each latent domain. We used the net.scores() function of the package EGAnet: this function estimates a score for each domain, starting from the standardized network loadings described above (all the exact calculations are available at https://cran.r-project.org/web/packages/EGAnet/vignettes/Network_Scores.html). In this way, the influence of the latent domain was a prior coded within the model, since we re-defined the latent domains as measurable entities that were normally distributed. The net.scores() function was able to define the scores for 1138 participants out of 1206. Consequently, the assumptions described above were respected. Moreover, to further reduce potential confounding brought by such latent scores, we encoded sets of whitelisted and blacklisted arcs. In order to combine such data-driven approach with a-priori knowledge, we defined a set of whitelisted arcs extracting this information from reviews, meta-analyses, longitudinal or cross-sectional research studying both the relations among variables belonging to different communities and the relations among the emerged latent domains. To get consistent results, we defined a direction only when at least a review/meta-analysis or two research articles provided the same result. To further minimize the risk that the communities scores could confound the original observed, we estimated the BN only on the community scores. Indeed, such a choice was more in line with the research questions and with the network scores theory. Such scores, in fact, represent composite and weighted variables than latent ones (Christensen, 2020).

We selected a PC constraint-based algorithm to learn the BN structure. Given the large set of nodes (observed and latent-derived), we decided to reduce the noise that such data could produce by using the model averaging approach. We set a threshold of 85% for the arc strength (i.e., the final BN will present arcs found in more than 85% of the simulated networks). The threshold for arc direction was defined by using the approach described by Scutari & Nagarajan (Scutari & Nagarajan, 2013). Considering the high starting number of arcs that from calculated by the PC algorithm, we set an alpha threshold of 0.01 to be more conservative and eliminate more potential false positive arcs. Moreover, we made a descriptive analysis for those latent nodes not directly connected with other latent nodes, to understand if there were indirect path passing through the original set of observed nodes. We performed all these steps on all the 1206 original individuals. Finally, we learned the network parameters. We used the bnlearn package (Scutari, 2010).

Results

Basics of network and exploratory graph analysis

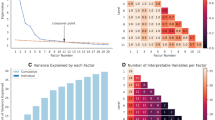
The EGA procedure (N = 663) led to the definition of a network consisting of seven communities (domains in the sequel; Fig. 1) reflecting, therefore, seven latent domains. The domain with the largest number of interconnected nodes, that we called Mental Health (MTL in the sequel), included measures assessing mental disorders (i.e., hostility and withdrawal behaviors, thought problems, anxiety, depression), personality aspects (i.e., conscientiousness, neuroticism and extraversion), sleep problems and other characteristics related to mental health (i.e., perception of rejection and stress, life satisfaction and self-efficacy). The domain entitled Externalizing problems (EXT) clustered measures detecting externalizing behaviors or mental disorders that contained such behaviors among their symptoms (hyperactivity disorders or antisocial personality disorder), as well as measures related to externalizing issues (i.e., rule-breaking and aggressivity behaviors). Interestingly, unlike the other personality traits – which were better characterized within the MTL domain – the Agreeableness subscale of the Neo-FFI questionnaire was included in the EXT domain.

Fig. 1
figure 1

The exploratory network and its seven communities.

Full size image

The EGA procedure extracted two separate communities focused on cognitive measures: The High-level Cognitive Functions (HCF) domain grouped cognitive measures that reflect high-level cognitive abilities including verbal intelligence, episodic memory, working memory, emotion recognition, spatial orientation, sustained attention. Separately, the Basic Cognitive Functions (BCF) domain comprised cognitive measures that tap lower-level processing abilities: processing speed, cognitive flexibility (card sorting task) and inhibition (flanker task).

Another domain (labeled as SUB) grouped together questions asking participants how many times they assumed illicit substances (in general) or marijuana (in particular) and how many drinks or tobacco products they usually assume within seven days. As such, this domain reflects substance use and abuse. The Delay Discounting Task (DD) domain was composed of the scores obtained in the DD that measures the discounting of delayed reward, with two different amounts of money (i.e., 200 and 40 K dollars). The domain called Pain (PAI) consisted of two measures detecting the perception of intensity of the pain and how much it interferes with the daily life.

The bootstrap procedure we applied to estimate the final network revealed that the model emerged was stable, namely it was consistently found in the 84% of the replications (i.e., 3360 out of 4000 replications). Furthermore, as described within the Methods section, we analyzed the goodness of fit of the model on another sample of 543 participants. All the indices described a good fit of the model to data (CFI: 0.943 RMSEA: 0.041[0.038-0.045]; SRMR: 0.063). Taken together, these results suggest that the seven-domains model reliably represents the structure of the data. We have also assessed the node stability, evaluating how many times a node belongs to the same domain across the (4000) replications. This information was provided by the node strength, a value that should overcome a threshold of 0.80 to be considered stable. All the initial 37 variables but one emerged to be stable, since they were related to the same domain most of the times. Indeed, the strength of the Openness (i.e., a subscale of the Neo-FFI questionnaire) node was under the threshold of 0.80, thus we decided to remove it from the network. We observed this clustering solution even when setting the tuning parameter to 0.2 or 0.7 (See Table S3 of Supplementary Material).

The network loadings also allowed us to better delineate the relationships both within and between the domains (Fig. 2). Within MTL domain, all the measures that indicated the presence of a mental disease or psychological dysfunction and suffering were positively associated with the domain, with high coefficients characterizing the relation. For example, depression (V10), neuroticism (V12) and perception of stress (V4) were positively linked to MTL with coefficients ≥ .302. On the other hand, measures depicting well-being and classically ‘positive’ psychological constructs (i.e., life satisfaction, self-efficacy, conscientiousness, and extroversion) were negatively linked to MTL, suggesting that the more a person shows a higher score in one of these four measures, the less would be the latent score of MTL (see Table 1).

Fig. 2
figure 2

Centrality indices of the 37 nodes of the network. Note: For the sake of simplicity, we rescaled the centrality values on a scale ranging from 0 (lowest value of centrality) to 1 (highest value of centrality). Such operation was made possible by the centralityPlot() function of the qgraph package (Epskamp et al., 2012)

Full size image
Table 1 Standardized network loadings of the 37 variables of the network to their communities.
Full size table

A similar scenario can be observed within the EXT domain, wherein all the measures indicating an externalizing-related behavior and attitudes were positively associated with the domain (ranging from .155 for the Antisocial Personality Problems to .425 for Externalizing Behaviors). As expected, the Agreeableness score was negatively associated with the domain (-0.171). The HCF and the BCF domains contained variables that were all positively related to them. For the HCF domain, the measure that was found less related to it was the Emotion Recognition (0.113) whereas the one with the highest score was represented by Progressive Matrices score, assessing Fluid Intelligence (0.357). Concerning the BCF domain, all the measures were similarly associated with the domain (from .284 for Processing speed to 0.42 for Cognitive flexibility).

Within SUB domain, all the variables were positively associated with the domain, with Tobacco assumption being the less related (.096) and assumption of marijuana the most related (0.547). The PAI and DD domains contained variables that have all high positive coefficients scores (i.e., ≥ 0.481).

Beyond the relationships within each domain, from Table 1 it is possible to examine also the relationships among latent domains. In particular, the MTL domain revealed to be related to all the other domains. The HCF domain showed a positive correlation with the BCF (r = .586, p < .001) and DD (r = .43, p < .001), and a negative correlation with the MTL (r = − .2777, p < .0001). The EXT domain was positively associated with PAI (r = .36, p < .001) and SUB (r = .497, p < .001) domains, while it was negatively associated with DD domain (r = − .142, p < .001). The DD domain was positively correlated with BCF (r = .138, p < .001), while it was negatively correlated with MTL (r = − .177, p = .01), PAI (r = − .151, p = .021) domains. Estimates from the confirmatory analysis were coherent (see Supplementary Material Table S4).

In order to deepen the structure of the network, we extracted the centrality indices, which enabled us to understand which nodes were more central in the network. We observed that nodes representing the crystallized intelligence (V24), depression (V10), externalizing behaviors (V31) and perception of stress (V4) were the nodes with the highest strength values, that is showing the highest number of connections inside the entire network (Fig. 3). Importantly, these four nodes reflected cognitive, well-being or mental health constructs showed the highest number of relationships with other constructs of the network.

Fig. 3
figure 3

The final bootstrapped Bayesian Network. Note: BCF stands for Basic-level Cognitive Functions, DD stands for Delay Discounting Task, EXT stands for EXTernalizing problems, HCF stands for High-level Cognitive Functions, MTL stands for Mental Health, PAI stands for PAIn, SUB stands for Substance use/abuse

Full size image

Considering closeness index, we observed that the most central nodes (i.e., values ≥ 0.9) of the network belong to the MTL domain (Fig. 2). This means that all these nodes were more frequently the closest to all the other nodes of the network. Therefore, the psychological constructs they reflect showed a higher number of direct relationships with other constructs, as compared with the rest of the selected constructs. Finally, Crystalized intelligence (i.e., node V24 in the Fig. 2) was the most central variable of the entire network in terms of betweenness, with its value that remarkably deviated from all the other nodes. This means that the ‘Crystalized intelligence node’ lied on the shortest path between other two nodes of the network more frequently than other nodes. Therefore, such measure of crystalized intelligence could, potentially, influence the relationship of the other two variables connected to it, since it was in the middle of their relationship. Notably, such node resulted to play a central role according to two out of three centrality indices. We obtained the same results even including the node V38 (see Supplementary Material Figure S1).

Bayesian network

Once the network was defined and the communities/clusters were detected, we needed to face the fact that this resulted model described only bidirectional influences among nodes or communities/domains. As introduced before, such model could hide a more complex organization, with potential influence pathways. Therefore, we decided to estimate a Bayesian Network (BN).

As typically done in BN approach, we first encoded previous knowledge about the connections among domains, through the so-called whitelisted arcs (i.e., connections between nodes), namely a set of arcs that must be included in the final BN (Scutari & Denis, 2014). To select the whitelisted arcs, we first considered the set of significant correlations among domains, as shown in Table 2. Then, we performed a brief and non-systematic literature research to make some preliminary assumptions on the potential direction of the relationships among these domains. To get consistent results, we defined a direction only when at least a review/meta-analysis or two research articles provided the same result (see Table S5 of Supplementary material to check references supporting such directions).

Table 2 The correlations among the seven domains and the proposed direction inferred from literature research
Full size table

The resulting BN (Fig. 3) had 7 nodes and 10 directed arcs. The used algorithm (see methods section) suggested a significance threshold for the arc detection equal to 0.749. In other words, each direction that appeared less than 74.9% of times across replications, was removed from the network (Scutari & Denis, 2014).

In terms of influence among nodes depicting domains’ scores, MTL directly influenced HCF (coefficient: -0.188), DD (coefficient: -0.082) and SUB (coefficient: -0.521) domains. The BCF domain directly influenced the HCF domain (coefficient: 0.518), which, in turn, influenced both DD and (coefficient: 0.449) SUB (coefficient: 0.173) domains. DD influenced the SUB domain (coefficient: -0.003). EXT influenced both MTL (coefficient: 0.838) and SUB (coefficient: 1.198) domains. Finally, PAI was influenced only MTL (coefficient: 0.683).

Discussion

In the present study we adopted advanced methodological approaches – the Exploratory Graph Analysis and Bayesian Networks– on a large database in order to highlight the distinct facets that characterize human mind and behavior, and to delineate their possible inter-relationships. Notably, this is the first study to explore and deepen the relations among a myriad of aspects that characterize the individual: from cognition to mental health, from pain to substance use, from quality of sleep to reward discounting. The ‘picture’ that came out comprises seven separate, but interrelated, domains: Mental Health (MTL), Externalizing problems (EXT), High-level Cognitive Functions (HCF), Basic Cognitive Functions (BCF), Substances use and abuse (SUB), Delay Discounting (DD) and Pain (PAI). This result follows a recent current of research reporting a low dimensionality of brain functional networks (Karolis et al., 2019) and behavior in both healthy individuals (Cona et al., 2019; Friedman & Miyake, 2017) and pathological population (Corbetta et al., 2015, 2018), whereby individual differences in cognitive performance/psychological traits or in deficits were effectively described by a low number dimensions/domains.

More specifically, cognitive functions can be clustered around two main domains, which differentiated High Cognitive Functions (HCF) from Low Cognitive Functions (LCF). As such, the present finding lies in between the g-factor (Spearman, 1904) and the Multiple-Factor theories (Gardner, 2000). The HCF functions comprise complex, multi-processes functions, such as fluid and crystalized intelligences, memory, and emotion recognition, and form a hierarchically higher domain. On the other hand, processing speed, flexibility, and inhibition (BCF) are part of a separate, hierarchically lower, domain. Functions of the BCF domain can be indeed conceptualized as processes that are necessarily implied in the HCF functions, but not vice versa. This idea is also corroborated by the Bayesian approach, which showed that BCF contributes and influences HCF domain rather than the opposite.

The literature is rich with studies exploring relationships among distinct cognitive functions (Ackerman et al., 2005; Buehner et al., 2006; Canivez & McGill, 2016), yet this is the first study to clearly highlight the existence of two separate domains in cognition and their possible causal relationships. To corroborate our view, it is not a coincidence that the two most prominent theories of cognitive aging - Processing Speed Theory (Salthouse, 1996) and Inhibitory Deficits Theory (Hasher & Zacks, 1988) – have emphasized the fact that the processing speed and inhibition, respectively, are the core mechanisms responsible for age-related impairments in other, higher-order, cognitive functions, thus suggesting their causal role. Furthermore, inhibition and flexibility/switching are typically considered two functions belonging to working memory construct (Miyake et al., 2000). Based on this, our findings are in agreement with the evidence that working memory and intelligence are different constructs (Ackerman et al., 2005).

Graph centrality indices revealed that crystalized intelligence was the most central variable of the entire network in terms of betweenness. As also illustrated in Fig. 1, crystalized intelligence exhibited connections with all the other domains. Among the various cognitive functions, indeed, crystalized intelligence is the one most strictly dependent upon other, not cognitive factors, as education and culture (Belsky, 1990; Furnham et al., 2005; Moutafi et al., 2004; Wood & Englert, 2009).

Notably, we found that MTL represented the largest community of nodes, comprising not only mental disorders (e.g., depression, anxiety) but a variety of dimensions, including personality traits, sleep problems, characteristics related to well-being and behaviors toward life and other people (e.g., life satisfaction, perception of stress and rejection). This finding led important insights revealing how personality traits, mood states, mental health and well-being variables are more strictly interconnected than thought in the past. Factors like neuroticism, anger levels, perception of stress and depression are those more related to the MTL domain. Importantly, life satisfaction, consciousness and extroversion resulted negatively correlated with MTL, thus they appeared to have a protective role on individual mental health. This pattern of results supports a very recent study (Santesteban-Echarri et al., 2020), which demonstrated that individuals with early signs of mental illness displayed a specific personality profile characterized by higher neuroticism, lower conscientiousness and lower extraversion. Our model successfully captures the dimensions and facets that are used to define externalizing behavior (Kauten & Barry, 2020), that is aggressiveness, rule-breaking behavior, antisocial behavior, hyperactivity and – negatively correlated – agreeableness. All these nodes have been indeed clustered under the umbrella term ‘externalizing behavior’ by our model. It is interesting to notice that, although related, mental health and externalizing nodes belonged to separate domains, with externalizing domain being more likely to influence mental health than vice versa. This is coherent with the evidence that externalizing behavior is indeed more common in childhood and decreases from early childhood to adolescence (Leve et al., 2005), whereas the occurrence of psychological disorders as anxiety and depression tends to increase in early adulthood (Copeland et al., 2014; Reinherz et al., 2003).

Previous research proposed that the spectrum of co-occurring symptoms and disorders underlying the externalizing domain share a common disinhibitory vulnerability (Bobova et al., 2009; Endres et al., 2011, 2014; Hicks et al., 2007; Krueger et al., 2009). Finn and collaborators(2014) suggested that the tendency to discount delayed rewards represents a common feature underlying externalizing psychopathology. Our study showed that Delay Discounting (DD) is separate from EXT. In fact, the Bayesian approach, however, did not reveal a clear direction among the two domains, but showed that DD is the ‘crossroad’ of four different domains: it receives direct influences from HCF and MTL, whereas it exerts influences on SUB domain, together with the EXT and MTL. This give support to the heterogenous nature of delay discounting as the result of both cognitive components, such as executive working memory capacity (Finn et al., 2014; Koffarnus et al., 2013), and motivational/emotional components (Frost & McNaughton, 2017). Delay discounting is indeed related to a constellation of cognitive and psychological variables(Cona et al., 2019; Rounds et al., 2007), somatic symptoms (Tompkins et al., 2016), sleep problems and high levels of stress (Chan, 2017; Lempert et al., 2012), perception of rejection, low levels of self-efficacy and life satisfaction, and substance addiction (Bickel et al., 2007). Moreover, as delay discounting has been associated with so many health-related behaviors, researchers have sought to establish whether time preference for reward is a result of, a simply a correlate, or a cause of, unhealthy behaviors (Koffarnus et al., 2013). Our study provides some clues on the possible causal role of delay discounting in substance addiction.

Substance use and abuse (SUB) domain comprises dimensions associated with marijuana and other drugs assumption, tobacco use and alcohol intake. Furthermore, SUB appears to be influenced by both MTL and DD domains, as well as by the EXT domain. This is in line with previous findings, suggesting that the externalizing factors can be strongly associated with substance use in adolescents and young adults (Pedersen et al., 2017) as well as the risk for alcohol use and dependence can be associated to a genetic susceptibility to externalizing disorders (Hicks et al., 2007; Kendler et al., 2003). Indeed, externalizing disorders have been shown to increase the risk of cannabis use initiation in adolescence independently of whether these behaviors appeared in the early childhood or were first manifested during adolescence (Hayatbakhsh et al., 2008). Also, although cannabis use and abuse may lead to symptoms that mimic externalizing behaviors, some longitudinal studies are in agreement with the present study in revealing that externalizing behavior problems predict cannabis use (Farmer et al., 2015; Griffith-Lendering et al., 2011). The results of our study seem to be in line with all these previous works, adding the fact that such association can assume a specific direction and not the opposite.

In other models, substance use (and abuse) can be the result of a triadic influence: Together with EXT, mental health and delay discounting may play a predictive role. This is in line with previous literature, which found that, for example, adults with alcohol dependence from adolescence to adulthood show higher rates of anxiety or depression diagnoses in adolescence (Meier et al., 2013). Interestingly, a recent meta-analysis highlighted that childhood depression, ADHD, conduct disorder, and oppositional deviant disorder increase the risk of for future substance-related disorders, whereas anxiety disorders do not seem to enhance the risk of developing substance-related disorders, even if the pattern of finding is highly mixed (Groenman et al., 2017).

The current research is not without caveats. First, our results are dependent on the selected measures of the HCP database. Adding or removing variables could lead to (even slightly) different results. We tried to face such issue by selecting the biggest set of variables possible. Second, we did not test the network on some demographic variables, such as gender. Future studies could insert some demographics to observe potential changes of network’s dynamics. Third, uncovering latent domains into score could have minimize the spurious relationships among the original observed variables, but more methodological and mathematical demonstration are required to further demonstrate such issue. Fourth, we run the analysis of the BN on the same sample. The size of our sample, despite large (i.e., 1206 individuals), could be increased to observe if the same results emerge. Finally, the review used to define the a priori arcs of the BN was nonsystematic.

Beyond the limitations, we showed that, by means of Exploratory Graph analysis and Bayesian Networks analysis, it is possible to observe how different human facets relate to each other. It is worth noting that the use of such a network approach, even if more data-driven oriented, it has been selected accordingly to what a network model is and what the associations among variables mean in such a model. As suggested by Christensen and Golino (2021), in a network model is the unique associations among nodes that define and “cause” the occurrence of a specific community. In factor models, on the other hand, the presence of latent factors “causes” the common variance of some observed variables (Bringmann & Eronen, 2018; Marsman et al., 2018). The starting point of the present study is the associations among variables since we could not assume a priori the existence of specific common factors. All the checks on the data structure and the results provided by the EGA seemed to corroborate our view. We cannot exclude that also factor models can provide similar structures, but their use was beyond the aim of such work. We found that while some facets share a common underlying dimension, other facets are instead separate and more independent from each other. In such a way, we drew an architecture of individual’s facets that can serve as model and guidance for future neuroimaging studies and clinical practice. First, this study could motivate new research in neuroscience field to get insights about how this architecture emerges from the topology of functional brain networks and the dynamic organization of its communities’ architecture. For example, are the seven domains associated with distinct functional networks at rest? Or can connectivity profiles be used to predict individual differences in cognitive/behavioral/psychological architecture? This line of research will potentially discover fMRI-based connectivity ‘neuromarkers’ of such architecture, which may eventually be used to personalize clinical and educational practices and improve outcomes. The HCP database could be the elective mean to successfully address these future questions as it also comprises fMRI sessions.

Second, the pattern of findings emphasizes the contribution of multiple sources to mental health problems, externalizing behaviors and substance addiction, charting the course for early detection of risk factors and intervention to prevent such disorders and unhealthy behaviors in later life.

Third, the integrated approach based on two network-based techniques allowed us to try brave choices (as using the network scores data to test Bayesian networks) that can pave the way for future studies aimed at creating a more methodological bridged between EGA and BNs.