Introduction

The model that Holland originally proposed in 1959 is the most widely known model that can account for the structure of interests in individuals (Darcy & Tracey, 2007). According to this model, individuals can be characterised by their affiliation with six distinct types. Each of these types describes specific preferences for certain work environments and activities. For example, realistic types prefer activities that require the manipulation of objects (e.g., tools or machines). By contrast, social types prefer activities that require interactions with others (Kaub et al., 2016). By taking the first letter of each type (Realistic, Investigative, Artistic, Social, Enterprising, and Conventional), this model is often called the RIASEC model. An important aspect of Holland’s theory is that the environment (the activities that are important in a workplace or study major) can also be classified using these six dimensions (Holland, 1966). The congruence hypothesis (see, e.g., Furnham, 2001) proposes that job or study satisfaction, performance on the job or at college/university, and well-being are related to the fit between person and environment, specifically between vocational interests and the environment (e.g., Brown & Gore, 1994). Therefore, this model is often applied in career counselling contexts and has been used as a basis for the development of widely applied instruments for assessing vocational interests (Darcy & Tracey, 2007). Even though the theory was developed for vocational settings and employed samples, it has since been successfully applied to academic samples. In such cases, the congruence between individual interests and study majors has been examined (Nye et al., 2012).

The aim of this study was to test the congruence hypothesis in a sample of German teacher students. In doing so, two methods were employed to examine congruence: the profile correlation and Response Surface Analysis (RSA). Results were then compared. The motivation for this research was twofold: First, we wanted to add to the sparse research on the applicability of the congruence hypothesis to the specific group of teacher students. Second, and more important, we applied RSA methodology to examine congruence effects in more detail than previous approaches. To our knowledge, this is the first study to use RSA methodology to test the congruence hypothesis in vocational interest research. Before we describe this study in detail, we summarise evidence for the congruence hypothesis and discuss two relevant issues (the determination of the environment and the determination of congruence).

The RIASEC model and the congruence hypothesis

As mentioned above, individual interests and environments can be classified or described with six interest domains (Holland, 1966). The fact that individual interests and the environment can be described by the same dimensions has helped interest-occupation congruence to become one of the major theories in the field of career development (Tracey, 2007).

As Holland (1966) preferred a typological approach for describing individual differences in interests, individuals are typically not described in terms of their scores on all six interest scales. Rather, they are described either in terms of the interest domain with the highest score or in terms of a three-letter code. The first letter of that code represents the interest domain with the highest score, and the second and third letters represent the domains with the second and third highest scores.

Additionally, the model also includes the assumption that some interest domains are more similar to each other than to other domains. In Holland’s model, interest domains are arranged in a hexagon, and distances within the hexagon reflect similarities between the interest domains. Adjacent interest domains are assumed to be the most similar, whereas interest domains on opposite sides of the hexagon are assumed to be the least similar (Nagy et al., 2010).

Despite criticisms (e.g., Tinsley, 2000) and competing models (see Nagy et al., 2010), Holland’s model is still widely used by practitioners (see McClain & Reardon, 2015) and has been used in recent research (e.g., Ferreira et al., 2016; Phan & Rounds, 2018). There is also evidence for the validity of the model. For example, using confirmatory factor analysis, Nagy et al. (2010) were able to confirm the assumptions about the relationships among the interest domains made by the hexagonal model with data from a sample of German high school and college students who completed a German interest inventory. Additionally, the authors found that the hexagonal model fit the data better than competing models. Sidiropoulou-Dimakakou et al. (2008) examined the applicability of Holland’s model in a sample of Greek university students. They found that the model could be applied to a Greek sample; however, some inconsistencies (e.g., the Realistic and Investigative types were more similar than expected) were also found.

It is assumed that person-occupation fit regarding vocational interests is associated with better outcomes, typically in terms of achievement or satisfaction (Tracey, 2007). Using the congruence hypothesis as a basis, career counsellors can obtain interest codes for a range of occupations or occupational groups from several sources (e.g., the Occupational Information Network, O*NET; see Eggerth et al., 2005) and compare them to the individual interests of their clients. Online tools such as the O*NET interest profiler link individual interest profiles to occupational profiles and determine the extent of fit (Kroustalis et al., 2010). Even though the theory was first developed for vocational settings, it has since been successfully applied to academic settings, where the congruence between individual interests and study majors has to be determined (Nye et al., 2012).

There is meta-analytic evidence for the validity of the congruence hypothesis. For example, a meta-analysis examining the relationship between congruence and satisfaction in vocational, academic, and military settings by Tsabari et al. (2005) found a mean correlation of .16 to .17 between the two variables, but only one study that examined congruence in an academic setting was included in their meta-analysis. An important result of the study by Tsabari et al. (2005) was that the choice of the congruence measure was a moderating factor, that is, a substantial part of the variation in the congruence-satisfaction relationship could be attributed to the choice of congruence measure. A later meta-analysis by Nye et al. (2012) found a mean correlation between congruence and performance in employed samples of .36. The study by Nye et al. (2012) also included 18 academic samples and additionally found substantial relationships in the academic setting (i.e., between .08 and .31 for the relationship between congruence and course grades and between .12 and .35 for the relationship between congruence and persistence; in both cases, the magnitude of the relationship depended on the instrument that was used to assess vocational interests).

To our knowledge, only a few studies have examined this issue in the field of teacher education. For example, Kaub et al. (2014) examined the relationship between interest-environment congruence and satisfaction with study content in a sample of German teacher student freshmen. The researchers applied two measures of congruence: a recently developed dimensional approach (using the metric information provided by the scales) suggested by Rolfs and Schuler (2002) and the C-Index, which compares the first three letters of the individual and environmental codes. When they used the dimensional congruence measure, the researchers found significant congruence-satisfaction relationships for teacher students who had chosen to teach either two science subjects or one science subject and one subject from the fields of languages or humanities. No significant congruence-satisfaction relationship was found for teacher students who intended to teach two language or humanities subjects. When the C-Index was applied, none of the congruence-satisfaction relationships were significant. Thus, the congruence hypothesis was partially supported, and Kaub et al. (2014) additionally found support for the assumption that findings are strongly influenced by the congruence measure that is used.

In another study, Swanson (2012) examined interest-environment congruence in a sample of language teachers from the US and Canada. Comparing individual and environmental three-letter codes, the researcher found that for the majority of teachers, the profile of individual interests was similar to the environmental assessment of the profession. Additionally, teachers with appropriate individual vocational interests were more likely to use appropriate coping styles. However, satisfaction or job performance were not assessed, so this study cannot be considered a test of the congruence hypothesis.

Determination of the Environment

A critical issue in this field of research is the question of how to identify a specific environment (e.g., occupation or study major) as environments are defined by the activities that are important in them. To examine the environment in an academic (college or university) setting, two approaches prevail. One approach involves using large data sets of successful students. The data set is then grouped by major, and the average score is computed for each of the six dimensions for each group. The mean scores on the six scales are then used as environmental scores for these groups (i.e., groups of students enrolled in the same major or family of majors). This procedure, also called psychosocial assessment (see Kaub et al., 2016), can be considered problematic as it is tacitly assumed that there must be congruence between individual interests and the environment (i.e., the study major) when the student is successful. Nonetheless, this approach has been used in several studies, for example, by Allen and Robbins (2010). Another approach that was used by Kaub et al. (2014) amongst others involves obtaining ratings from lecturers. Kaub et al. (2016) argued that this latter approach leads to more objective and valid assessments.

Determination of congruence

The second critical issue in this line of research involves the question of how to determine congruence, for which several approaches have been suggested. The first indices that were proposed (for an overview and empirical examination, see Brown & Gore, 1994) defined congruence as the match (vs. lack of match) between the first letter of the individual code (i.e., the interest domain with the highest score for that individual) and the first letter of the environmental code or as the number of matches between the first two or all three letters of the two codes (e.g., the C-Index proposed by Brown & Gore, 1994). This definition of congruence can be considered problematic for three reasons. First, these indices do not take the metric information provided by the scores into account. Second, ties might occur when creating the codes (i.e., scores on two or more dimensions are identical), and there is no clear decision rule regarding which letter should be included at the relevant position of the code (de Fruyt, 2002; Rolfs & Schuler, 2002). Third, these indices take into account a maximum of only three out of the six dimensions.

More recent approaches employ the metric information that can be gleaned from all six dimensions. One of these approaches defines congruence as the correlation between the profile of individual interests and the environmental scores (the profile correlation; Kroustalis et al., 2010). When computing the profile correlation, a correlation of six pairs of scores (the six dimensions of the RIASEC model) is computed for each individual. The size of the profile correlation indicates the degree of accordance between the rank orders of the individual interest and environmental scores and can be correlated with, for example, job or study satisfaction.

Despite recent progress in the development of congruence indices, Nye et al. (2012) criticised that the established congruence measures reduce a multidimensional problem into a single score and suggested the use of polynomial regression to examine the congruence hypothesis. Polynomial regression differs from standard (multiple) regression in that, in addition to including the original predictors and the interaction between them, it also includes higher order terms of the predictors (e.g., x2) as additional predictors. Polynomial regression is typically seen as a way to capture nonlinear relationships between predictors and an outcome variable (Cohen et al., 2003, p. 196). However, the results of polynomial regression can be difficult to interpret if the results are not plotted as a three-dimensional response surface (Schönbrodt, 2016). Therefore, Response Surface Analysis (RSA) is based on polynomial regression and can facilitate the interpretation of the relationships between two predictor variables and one outcome variable, making it especially suitable for examining congruence-outcome relationships (Shanock et al., 2010). RSA methodology has already been used in psychological research: for example, Milatz et al. (2015) used this technique to investigate the effects of relationship quality with students and attachment security on burnout among elementary school teachers. The effects of implicit and explicit power motives on wellbeing among teachers were the focus of another study (Wagner et al., 2016). Two important lines in the context of the RSA are the line of congruence (LOC, the line with congruent predictor combinations, Y = X) and the line of incongruence (LOIC, perpendicular to the line of congruence, Y = −X), both of which are located in the XY plane at the bottom of the graph (see, e.g., Fig. 1 in the results section). To examine congruence, first, the first principal axis (i.e., the ridge of the response surface) is examined. For a perfect numerical congruence effect, the projection of the first principal axis on the XY plane should equal the LOC, which indicates that the outcome is highest when the values of the two predictor variables are equal. Second, the surface above the LOIC is examined. It should be an inverted U-shape, and the maximum of this curvature should be located at the congruent predictor combination of Y = X = 0 (Humberg et al., 2019). RSA methodology provides not only a plot, but also significance tests for the underlying parameters (which are derived from the beta weights of the polynomial regression analysis). To examine congruence, parameter a4, which describes the curvature of the surface above the LOIC, is the most important parameter; it must be significantly negative to indicate congruence.

The use of RSA methodology is often compared to the use of difference scores, i.e., the absolute difference (|X – Y|) between individual interest and environmental scores in this case. More discrepant individual interest and environmental scores lead to larger absolute differences, so difference scores describe the discrepancy of the two scores. Several authors have argued that RSA methodology is better suited for the examination of a congruence hypothesis than the use of difference scores (which are then correlated with the outcome) because difference scores cannot be used to determine the effects of single predictors (Nestler et al., 2019; Shanock et al., 2010). Additionally, the use of difference scores is based on the assumption that the two predictors are assessed on commensurable scales (i.e., the two predictors have a common anchor, e.g., a natural zero point) and that there is no effect of the mean level (i.e., the value of the outcome variable depends only on the congruence of the predictor variables and not on their absolute values). RSA methodology can handle predictors with incommensurable scales and allows researchers to test whether certain constraints (e.g., no mean level effect) hold (Schönbrodt, 2016). When conducting RSAs to examine the congruence of vocational interests and the environment, each of the six dimensions of the interest model is analysed separately. So, the use of RSA methodology answers Nye et al.’s (2012) call in two regards: First, this multidimensional problem is not reduced to a single score; second, a procedure based on polynomial regression is used.

Aim of the present study

The aim of the present study was to test the congruence hypothesis in a sample of German teacher students striving to teach a variety of subjects in several types of schools (see the Participants and Procedure section for more details about the sample). Satisfaction with course content was used as the dependent variable. To assess the environment, ratings were obtained from lecturers. Regarding the congruence measure we used, two methods were employed: Answering Nye et al.’s (2012) call to use polynomial regression to examine congruence, we applied RSA methodology to this issue. In addition, we computed the profile correlation between individual interests and the environmental profile of the study major as described by Kroustalis et al. (2010). To our knowledge, this is the first study to use RSA to investigate the congruence between individual interests and environmental scores.

As mentioned above, there is meta-analytic evidence for the validity of the congruence hypothesis in general (Tsabari et al., 2005) and in academic settings (Nye et al., 2012). Additionally, Kaub et al. (2014) partially confirmed the congruence hypothesis in a sample of German teacher students. Therefore, we expected to find a positive relationship between interest-environment congruence and satisfaction with course content when using the profile correlation (Hypothesis 1) and RSA (Hypothesis 2). While the profile correlation indeed reduces the issue to a single score, RSA methodology can be used to examine complex relationships between interests, environment, and the outcome (i.e., satisfaction with course content). For example, RSAs might reveal that the relationship between congruence and the outcome is nonlinear or that the outcome is affected only by the strength of interests. Additionally, patterns are analysed for each dimension of the interest model separately, so RSAs might reveal different relationships between interests, environment, and the outcome for the six interest dimensions. Therefore, an exploratory research question was whether complex relationships between interests, environment, and the outcome would be found. If so, the use of RSA methodology would be warranted in future studies on this issue.

Because the structure of teacher training in Germany might be different from the structure in other countries, we provide a brief explanation here. Future teachers enrol in a specialised teacher training programme at university, requiring them to select which type of school they want to teach in as well as (typically) two school subjects they intend to teach. In this federal state, teacher students can choose from five types of schools: elementary schools (Grades 1 to 4 where Grade 1 is the first year of mandatory schooling in Germany); two types of secondary school: middle school (‘Realschule plus’, Grades 5 to 10) and high school (‘Gymnasium’, Grades 5 to 13); special schools (designed for teaching students with special educational needs who attend these schools instead of secondary schools); and vocational schools (individuals who completed secondary schooling and chose formal vocational training attend these schools in addition to being trained on the job). Study programmes reflect upon the various school types by adjusting the composition of courses to the demands of the respective school type. While programmes for secondary schools focus on the content of the subjects (teacher students take courses in their subjects as well as educational science courses), programmes for elementary and special schools offer broader content (in addition to courses in their subjects as well as educational science courses, teacher students take courses in elementary or special education). When studying in this federal state, individuals have to complete both a Bachelor’s and a Master’s degree to become certified as a teacher. To sum up, the aim of this study was to examine the congruence hypothesis among teacher students. Hypothesis 1 predicted a positive relationship between interest-environment congruence and satisfaction with course content when applying the profile correlation as a measure of congruence. Hypothesis 2 predicted that confirmation of the congruence hypothesis can be found applying RSA.

Materials and methods

Participants and procedure

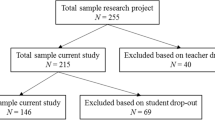
College/university students completed paper-and-pencil questionnaires in educational science courses at the start of the 2018–2019 winter term at a German university on a voluntary basis. The participants could complete these questionnaires during their regular courses, and no financial compensation was offered. Amongst other measures, they completed instruments that assessed their vocational interests, their satisfaction with the course content, and some demographic and contextual information (e.g., type of school). In total, N = 1789 students completed the questionnaires; however, n = 228 participants indicated that they did not intend to become a teacher (educational science courses are open to students from a wide range of study programmes), so their data were excluded from our analyses as we intended to focus on teacher students. In the first step of data screening, data from n = 16 participants had to be discarded because the information they provided about their school subjects was implausible or they had indicated that they had not yet chosen the type of school they intended to teach in later. In the next step of data screening, data from n = 226 participants was discarded as these participants had either indicated they intended to teach in vocational schoolsFootnote 1 or one of their school subjects was arts or ‘economics and labour’ (German ‘Wirtschaft und Arbeit’).Footnote 2 Finally, data sets from n = 148 participants had missing data on relevant variables (vocational interests, satisfaction with course content, type of school, and subjects studied), so these cases were also excluded from the analyses.

The sample included in the analyses consisted of N = 1171 teacher students. The majority of these students were female (70%); 24% were male; the remaining participants either identified their gender as diverse or did not indicate their gender. Participants’ mean age was M = 21.26 (SD = 2.60) years (Range: 16 to 38 years; 16 participants did not indicate their age). Most participants were bachelor students (n = 989); n = 182 were master level students. Most students intended to teach in elementary schools (n = 577) or high schools (n = 336). Other students intended to teach in special schools (n = 184)Footnote 3 or middle schools (n = 74). Teacher students in our sample had selected two out of 16 subjects (see Table o1 in the online materials). In total, 75 combinations of school subjects were present in our teacher student sample; the most frequent one was the combination of German and English (n = 100).

To obtain an assessment of the environment, lecturers responsible for every school subject that was present in our student sample were contacted in August 2020. Additionally, lecturers responsible for educational science courses as well as elementary education and special education courses were contacted. In total, 527 lecturers were contacted by email, and 177 of them completed the online survey (34%). Data provided by four lecturers had to be omitted from the analyses as they had left out a substantial number of items (between 19 and 48 out of 48 items). Data from lecturers was analysed separately for each subject as well as educational science courses, elementary education, and special education courses. If fewer than three participants could be found for a subject/group of courses, no environmental score was computed as it was questionable whether the information they provided could be considered representative. This criterion applied only once: No environmental scores for art courses were computed (data from teacher students intending to become art teachers were discarded as well). Data from six lecturers responsible for courses in ‘economics and labour’ were discarded as we had decided not to include teacher students who studied this subject in our sample.

Measures

Vocational interests

To assess students’ vocational interests, we used a 48-item instrument that was developed for research purposes.Footnote 4 We chose it because it can be used for free, and it is somewhat shorter than established German instruments, such as the 60-item AIST-3 (Bergmann & Eder, 2019). Each item on this instrument described a work activity, and participants had to indicate how much they were interested in that activity on a 5-point Likert scale (1 = ‘not at all’ to 5 = ‘very interested’). Eight items were assigned to each of the six RIASEC scales. Scale scores for the participants were created by computing the mean of the corresponding items. In an unpublished previous study (N = 149), the internal consistency (Cronbach’s α) of the six RIASEC scales ranged from α = .81 to α = .95. As part of this previous study, correlations between the scales from this instrument and the AIST-3 scales (Bergmann & Eder, 2019) were computed; the correlations between the corresponding scales (convergent correlations) ranged from .77 to .92 (all correlations were significant after the alpha-level adjustment). Internal consistency (Cronbach’s α) was acceptable in the present study as well, ranging from α = .78 to α = .88. In the present study, for participants who had omitted more than two items from a particular scale, no mean score was computed (teacher student participants with missing values were later excluded from the analyses).

Satisfaction with course content

We used a popular German instrument developed by Spies et al. (1996). Three items were used to assess satisfaction with course content. Each item consisted of a statement (sample item: ‘Overall, I am satisfied with my current course of study’; translated by the authors),Footnote 5 and participants had to indicate how well it applied to them on a 10-point Likert scale (1 = ‘does not apply to me at all’ to 10 = ‘applies completely to me’). The mean of the three items was computed and served as an individual’s satisfaction score. For participants who had omitted any of the three items, no mean score was computed (teacher student participants with missing values were later excluded from the analyses). Cronbach’s α was acceptable (α = .88) for this scale in the present study.

Demographic and contextual variables

Several demographic and contextual characteristics were assessed. Out of these, information about the study programme, type of school, and the school subjects chosen were analysed in the current study. This information was used to determine environmental profiles for different groups of teacher students.

Assessment of the environment

To assess the environment, we used the same 48 items that had previously been used to measure students’ interests. For the environmental assessment, the lecturers were asked to indicate the importance of each of the 48 activities for participating in their courses. Again, a 5-point Likert scale was used (1 = ‘not at all’ to 5 = ‘very important’). The internal consistency of the scales in the sample of lecturers was acceptable; Cronbach’s α ranged from α = .73 to α = .94. Like the interest scale scores, the environmental scale scores were computed as item means. To investigate the agreement between judges, ICCs (model: two-way, type: agreement, unit: average) were computed separately for the lecturers from each of the 16 subjects, the lecturers responsible for the educational science courses, and the lecturers responsible for the elementary education and special education courses. For more information about the computation of the ICC values, see the manual for the irr package (Gamer et al., 2019) from the R statistical environment (R Core Team, 2021), which had been used to compute the ICC values. The ICC values ranged from .73 to .96 and could be considered sufficient.

Data analysis

As described above, the ratings provided by the lecturers were averaged for each subject separately. So, for each of the 16 school subjects, the educational science courses, and the elementary education and special education courses, there were assessments of the environment regarding each of the six RIASEC variables (environmental scores).

As mentioned above, in the German teacher education system, teacher students take courses in two school subjects of their choice (usually offered by the relevant department at the university, e.g., mathematics) as well as educational science courses. Students who intend to teach in elementary or special schools additionally take courses in elementary or special education, respectively. For students who intend to teach in high or middle schools, the environment was determined by averaging the environmental scores for the two chosen school subjects as well as the environmental scores for the educational science courses (the average was computed separately for each RIASEC dimension). For students intending to teach in elementary or special schools, the environment was determined by averaging the environmental scores for the two chosen school subjects, the environmental scores for the educational science courses, and the environmental scores for elementary or special education courses, respectively (the average was computed separately for each RIASEC dimension). The variables that had been computed as described above were then used as measures of the respective environment.

To determine the profile correlation, we followed the procedure described by Kroustalis et al. (2010): For each individual, a correlation of six pairs of scores (the profiles of individual interest scores and environmental scores) was computed. Because correlations are restricted in range and therefore cannot be normally distributed, this score was transformed using Fisher’s Z transformation and used as indicator of interest-environment congruence for that individual. In the next step, the (Pearson) correlation between the transformed score and satisfaction with course content was computed to test the congruence hypothesis, where a statistically significant correlation would indicate confirmation of the congruence hypothesis.

For the RSAs, we could not test for numerical congruence as the two predictor variables (the individual vocational interest and environmental scores) were assessed with scales that each used an arbitrary metric. Even though both variables were assessed using the same 5-point Likert scales, they cannot be considered commensurable due to the lack of a common anchor (like a natural zero point). For example, the meaning of the response option ‘not at all’ might be understood differently by faculty than by teacher students (Schönbrodt, 2016). Standardizing the variables would not solve the issue as a common anchor would still lack. RSA methodology is suited to work with incommensurable predictor scales. In this case, the assumption is examined that an above-average level of vocational interest on a particular dimension should be associated with greater satisfaction with course content in a study environment that has an above-average environmental score on that dimension. Consequently, a below-average level of a particular dimension of vocational interest should lead to greater satisfaction when the environmental score regarding that dimension is also below average. This kind of RSA is called testing for fit patterns by Schönbrodt (2016). In this case, RSA is conducted in the same manner as it is for commensurable scales, but certain interpretations are not allowed (e.g., that the outcome is optimal when y is one unit smaller than x) (Schönbrodt, 2016). Individual interest and environmental score variables were z-standardised by their respective mean and standard deviation as described by Schönbrodt (2016) to ease interpretation. Separate RSAs were computed for each of the six dimensions. Individual interest and environmental score variables were included as predictor variables (variables x and y in the terminology of polynomial regression), and satisfaction with course content was included as the dependent variable (variable z in the terminology of polynomial regression).

RSAs were computed using the RSA package (Schönbrodt & Humberg, 2021) for the R statistical environment (R Core Team, 2021), which computes several models with different complexity (interaction model, rising ridge model, shifted rising ridge model, shifted and rotated rising ridge model, shifted squared difference model, shifted and rotated squared difference model, basic squared difference model, full polynomial model). Each model implies certain constraints or assumptions; for example, the shifted rising ridge model makes the assumption that there is a mean level effect (the ridge rises) and that the highest outcome results if one of the predictors differs systematically (by the shifting constant C) from the other predictor instead of being equal (the ridge is shifted away from the LOC). For an overview and a detailed explanation of these models, see Schönbrodt (2016). For each of the six dimensions, the best-fitting but most parsimonious model was selected and interpreted. As described above, by selecting a certain model, certain constraints or assumptions are implied. Model selection was based on the AICc because other criteria (e.g., the CFI or likelihood ratio test) have shortcomings when used for this purpose (Schönbrodt, 2016). The Akaike information criterion (AIC) is a measure of fit which can be used for model selection (Burnham & Anderson, 2004). When computing the AIC, a penalty is taken into account for each variable included in the model which rewards the choice of a parsimonious model (Field et al., 2012, p. 263). The corrected criterion (AICc) was suggested to be used with small sample sizes; when the sample size is large, the AICc converges to the AIC (Burnham & Anderson, 2004). Moreover, the model weight (i.e., the probability that this model was the best model from the set of candidate models, given the data; Wagenmakers & Farrell, 2004) provides additional information about the suitability of the selected model. For the congruence hypothesis to be properly tested, both predictors (the individual interest and environmental scores) have to be included in the model. Therefore, models that did not include both predictors (null model, only x, only x2, only y, only y2) were not considered.

Results

Mean scores on vocational interests and satisfaction with course content in the student sample can be found in Table 1. The average environmental scores can be found in Table 2. More detailed information about environmental scores can be found in Table o1 in the online materials.

Table 1 Mean interest and satisfaction scores in the student sample
Full size table
Table 2 Environmental assessment by faculty
Full size table

Results from the profile correlation

To test Hypothesis 1, the profile correlations between the individual interest profile and the environmental profile were calculated as described by Kroustalis et al. (2010) for each student separately (possible range: −1 to +1). The mean correlation value was M = .37 (SD = .27; Range: −.76 to .83). Then, the profile correlation scores were transformed by applying Fisher’s Z transformation (for the transformed variable: M = 0.42; SD = 0.32; Range: - 0.99 to 1.18). In the next step, the (Pearson) correlation between the transformed variable (as a measure of congruence) and satisfaction with course content was computed. This correlation was r = .21 (p < .001, two-tailed).Footnote 6

RSA results

To test Hypothesis 2, separate RSAs were computed for each dimension of the RIASEC model. In a first step, we determined which model provided the best fit for that dimension. In a second step, the parameters of the selected model were plotted and interpreted. Interpreting the model parameters also allowed us to examine the exploratory research question.

Artistic

Model comparisons revealed that the shifted squared difference model (SSQD model) was the best-fitting model for the artistic dimension (Table o2 in the online materials). It had the lowest AICc, a model weight of .21, a CFI of 1.00, and an adjusted R2 of .02. In the SSQD model, the ridge is flat but shifted laterally away from the LOC. Table 3 provides the coefficients for the SSQD model. Figure 1 (Panel A) shows the corresponding response surface. The nonsignificant parameter a4 (curvature of the surface above the LOIC) indicates that there was no congruence effect. Instead, the response surface shows decreasing satisfaction when artistic interest was low and the environmental assessment of the artistic dimension was high. When artistic interest was high, it seemed to make no difference whether the respective environmental assessment was low or high.

Table 3 Regression coefficients b0 to b5 and derived model parameters for the SSQD model (Artistic dimension)
Full size table
Fig. 1
figure 1

Response surfaces for the six RSA analyses. Note. The lines in the XY planes of the graphs represent the line of congruence (congruent predictor combinations) and the line of incongruence (perpendicular to the line of congruence).

Full size image

Conventional

According to the AICc, the shifted and rotated squared difference model (SRSQD model) was the best-fitting model for the conventional dimension (Table o3 in the online materials). It had a model weight of .22, a CFI of 1.00, and an adjusted R2 of .02. In the SRSQD model, the ridge is flat but shifted laterally and rotated away from the LOC. Table 4 provides the coefficients for the SRSQD model. Figure 1 (Panel B) shows the corresponding response surface. Parameter a5 is additionally computed when the ridge is rotated; it indicates the extent to which the ridge differs from the LOC (Schönbrodt et al., 2018). If the ridge is rotated, the parameter a′4 should be interpreted instead of a4 when determining congruence (Schönbrodt, 2016). Its nonsignificance indicates that there was no congruence effect. The response surface shows that satisfaction increased when both conventional interest and the corresponding environmental assessment were high.

Table 4 Regression coefficients b0 to b5 and derived model parameters for the SRSQD model (Conventional dimension)
Full size table

Enterprising

For the enterprising dimension, the full polynomial model was the best-fitting model (Table o4 in the online materials). It had the lowest AICc, a model weight of .23, a CFI of 1.00, and an adjusted R2 of .05. In the full polynomial model, there are no constraints on the regression weights. There are no assumptions that the ridge is shifted, tilted, or rotated. The coefficients for the full polynomial model are provided in Table 5. Figure 1 (Panel C) shows the corresponding response surface. Again, the nonsignificant parameter a4 (curvature of the surface above the LOIC) indicates that there was no congruence effect. The response surface shows a rather complex pattern. The highest satisfaction occurred when enterprising interest was high, irrespective of the level of the corresponding environmental assessment. A lower enterprising interest was associated with lower satisfaction, and this decline was even stronger when the environmental assessment was high (see Fig. 1, Panel C).

Table 5 Regression coefficients b0 to b5 and derived model parameters for the full polynomial model (Enterprising dimension)
Full size table

Investigative

For the investigative dimension, the onlyx model (investigative interest [x] as the only predictor) was the best-fitting model according to the AICc (Table o5 in the online materials). As mentioned above, one of the guidelines we followed was to consider only models that included both predictors (interest and environmental scores). Therefore, we chose the additive model, which ranked second according to the AICc. The ∆AICc for the additive model was only 1.31, which means that the fit of this model could be interpreted as essentially equally as good as the fit of the onlyx model (Schönbrodt, 2016). The additive model had a model weight of .15, a CFI of .98, and an adjusted R2 of .06. In the additive model, only the main effects of both predictors (interest and environmental scores) are included with no constraints on their regression weights. The surface of the additive model is flat (i.e., is has no ridge), so the selection of this model contradicts the assumption of a congruence effect. The coefficients of the additive model are provided in Table 6. Figure 1 (Panel D) shows the corresponding response surface. Investigative interest was positively associated with satisfaction. By contrast, the corresponding environmental score was unrelated to satisfaction.

Table 6 Regression coefficients b0 to b2 and derived model parameters for the additive model (Investigative dimension)
Full size table

Realistic

According to the AICc, the shifted and rotated rising ridge model (SRRR model) was the best-fitting model for the realistic dimension (Table o6 in the online materials). It had a model weight of .30, a CFI of 1.00, and an adjusted R2 of .01. In the SRRR model, the ridge is allowed to be tilted (i.e., there is a mean level effect), shifted laterally, and rotated. Table 7 presents the coefficients from the SRRR model. Figure 1 (Panel E) shows the corresponding response surface. Parameter a′4 (which should be interpreted instead of a4 when the ridge is rotated) was significantly positive and indicated that there was no congruence effect. For the congruence hypothesis to be confirmed, the parameter should be significantly negative. The response surface shows that the highest satisfaction occurred when the environmental assessment for the realistic dimension was high, irrespective of the level of realistic interest.

Table 7 Regression coefficients b0 to b5 and derived model parameters for the shifted and rotated rising ridge model (Realistic dimension)
Full size table

Social

Model comparisons revealed that the shifted squared difference model (SSQD model) was the best-fitting model for the social dimension (Table o7 in the online materials). It showed the lowest AICc, a model weight of .27, a CFI of 1.00, and an adjusted R2 of .03. In the SSQD model, the ridge is flat but shifted laterally. Table 8 presents the coefficients from the SSQD model. Figure 1 (Panel F) shows the corresponding response surface. Again, the nonsignificant parameter a4 (curvature of the surface above the LOIC) indicates that there was no congruence effect. The highest satisfaction occurred when social interest was high and the corresponding environmental score was low.

Table 8 Regression coefficients b0 to b5 and derived model parameters for the shifted squared difference model (Social dimension)
Full size table

Discussion

The major aim of this research was to examine the congruence hypothesis in a sample of German teacher students and to add to the sparse research findings regarding the congruence hypothesis in the context of teacher education. According to the congruence hypothesis (e.g., Brown & Gore, 1994), satisfaction with course content should increase as individual interest and environmental scores (i.e., activities important for studying the chosen major) become more similar (congruent). Two approaches were used to determine congruence: the profile correlation between the individual profile of interests and the environmental profile as described by Kroustalis et al. (2010) and RSA methodology. Hypothesis 1 predicted that confirmation of the congruence hypothesis (i.e., a positive relationship between interest-environment congruence and satisfaction with course content) could be found using the profile correlation, while Hypothesis 2 predicted confirmation of the congruence hypothesis by means of RSA methodology. The findings obtained with the profile correlation supported the congruence hypothesis, even though the correlation between congruence and satisfaction with course content was rather low. Thus, Hypothesis 1 was supported. As an explanation for the relatively weak (but statistically significant) correlation between congruence and satisfaction, it should be noted that satisfaction with course content is influenced by a wide range of factors. Tsabari et al. (2005) argued that a contribution to the explained variance of around 5% to 10% can be considered meaningful in that context. Additionally, Tracey (2007) pointed out that individuals are able to choose their environment (i.e., a programme of study) and are likely to choose one that fits their interests or to leave an environment (i.e., change their field of study) if they decide that it is unsuitable. Therefore, it would be unlikely for us to find an enormous amount of variance in interest-environment congruence that could be related to outcome measures, making a high congruence-outcome correlation unlikely. Our finding of support for the congruence hypothesis is in line with several previous studies that examined the congruence-satisfaction relationship in an academic setting: for example, the study by Allen and Robbins (2010), who also employed the profile correlation, or some of the findings by Kaub et al. (2014), who had examined this question in a sample of German teacher students using a similar congruence measure. The size of the mean profile correlation in our study (i.e., the congruence between individual interests and the selected course of study; M = .37 before correcting for restricted variance) stands out. The value is higher than the mean profile correlations reported by Allen and Robbins (2010) for two samples of U.S. college students (M = .22 and M = .14). However, Allen and Robbins (2010) applied a psychosocial approach for determining the environment, whereas we asked experts (i.e., faculty) for ratings. Therefore, the findings cannot be compared directly.

By contrast, the findings obtained with RSA methodology did not support the congruence hypothesis. None of the six RSAs revealed a saddle-shaped surface (i.e., a significant negative a4 or a′4 parameter), which would indicate congruence. So, Hypothesis 2 was not supported. As conclusions regarding the congruence hypothesis differ by the analytical approach employed, possible explanations (i.e., differences between the analytical approaches) should be mentioned. The first and most obvious difference is that each dimension is analysed separately in case of RSA methodology while the six dimensions are analysed simultaneously in case of the profile correlation. Second, when using RSA methodology, satisfaction with course content is predicted by the environmental and individual interest scores. Contrastingly, the profile correlation is computed as a measure of congruence which is then correlated with satisfaction with course content. Eventually, these differing findings are in line with the meta-analytical results by Tsabari et al. (2005) who found that conclusions regarding the congruence hypothesis were influenced by the analytical approach used.

Nevertheless, in investigating the exploratory research question, some interesting insights emerged. First, the RSAs showed that the associations between interests and environmental scores in the prediction of satisfaction with course content differed across the six interest domains. For example, individuals with higher investigative interest showed higher satisfaction with course content, independent of the corresponding environmental score. By contrast, the patterns in the other five domains were more complex. This finding highlights one advantage of RSA over previous two-step approaches: With RSA, it is possible to gain more differentiated insights into differences in the interest-environment-satisfaction associations across the interest domains. This advantage of the RSA methodology compared to difference scores or other traditional approaches was also found by Milatz et al. (2015) who examined effects of relationship quality and attachment security on burnout. Second, it is noteworthy that all interests, except realistic interest, had a main effect on satisfaction. This finding suggests that higher interest is generally associated with greater satisfaction with course content, even though the whole shape of the response surface should be taken into account for a complete interpretation of the results and the examination of the congruence hypothesis. These main effects are in line with the meta-analytic findings by Nye et al. (2012) who also reported significant relationships between (the absolute values of) interest scores and course grades. It should be noted that none of the six selected models could explain a substantial amount of variance (R2adj ≤ .06), which, according to Schönbrodt (2016), is a criterion that can be used to evaluate the performance of a model after it is selected. As we selected one of the best-fitting models from a group of models suitable for examining congruence, this finding also indicates that the RSAs did not provide support for the congruence hypothesis. Coming to our exploratory research question (whether the use of RSA is warranted as it can be used to examine more complex relationship patterns), our findings indicate that the use of RSA is warranted because complex patterns emerged that could not be captured by the profile correlation or other traditional indices of congruence.

Regarding the validity of the congruence hypothesis, an unequivocal conclusion cannot be drawn. Obviously, the congruence hypothesis holds when the six dimensions are analysed simultaneously (i.e., using the profile correlation), which can be called global congruence. As mentioned above, the RIASEC model is often used in career counselling. In this context, all dimensions are typically considered simultaneously. Therefore, an implication for practitioners is that the RIASEC model is an appropriate model to use in career counselling; it can even be used when an advice seeker is determined to become a teacher but is unsure about which type of school and which school subjects might be best for them. However, if possible, a dimensional approach should be used to examine congruence in counselling settings, as Kaub et al. (2014) found that the congruence hypothesis only held when a dimensional approach was applied.

By contrast, results obtained using the RSA methodology indicated that the congruence-satisfaction relationship might be more complex, and the relationship might differ depending on the dimension of the interest-structure model examined (domain-specific congruence). An implication for researchers is that more research should be conducted on domain-specific congruence. For this purpose, RSA methodology and other applications of polynomial regression can be used.

Regarding the transferability of our findings, an important limitation of the present study is that our sample consisted exclusively of teacher students, so the range of individual interests might have been narrower than in more heterogeneous samples. Second, the assessment of the environment was difficult as teacher students in Germany take courses in the two school subjects they select as well as courses in the educational sciences. Teacher students who intend to teach in elementary or special schools additionally take elementary or special education courses, respectively. We asked the lecturers to rate their courses and later averaged these ratings. We cannot rule out the possibility that this approach was inaccurate; however, it seems difficult to imagine a better approach given the structure of teacher education in Germany.

We think that an important conclusion of this research is that interest-environment-satisfaction associations are more complex than shown by difference scores or other traditional approaches. More research on the congruence hypothesis using RSA methodology is needed to obtain more reliable results on this issue. Future research might especially want to examine the congruence hypothesis in a more heterogeneous sample and use objective measures (e.g., course grades) as the dependent variable.