Introduction

The most recent prevalence estimation of problem and pathological gambling in Sweden has shown that among 16–87 year olds as many as 1.3% are problem gamblers, and 0.6% have a severe gambling problem (Public Health Agency of Sweden, 2019). The relative commonness of problem gambling highlights the importance of providing effective treatment options and among psychological therapies, cognitive and behavioral therapy (CBT) is the most promising (Cowlishaw et al., 2012). CBT is intended to help stop a gambling behavior by helping the patient acquire specific skills and create awareness of certain thoughts and behaviors connected to the addiction. Such skills could for example be recognizing triggers or finding effective strategies to abstain from gambling.

Another common technique in CBT for pathological gambling is the restructuring of cognitive distortions related to gambling (Ladouceur et al., 2001; Petry et al., 2006; Raylu & Oei, 2010). Cognitive distortions in gambling are various irrational beliefs held by gamblers concerning the amount of control gamblers have over the game’s outcome or the nature of random events. There seems to be no clear consensus in the literature regarding exactly how many and what type of distortions gamblers entertain. In a review by Fortune and Goodie (2012) eight specific distortions were identified: the “Gambler’s Fallacy” (in which the gambler believes that if a certain outcome of a random event happens several consecutive times it increases the likelihood for the opposite outcome), “Overconfidence” (a disproportionate belief in one’s knowledge and skill), “Trends in number picking” (using certain patterns or rules when picking numbers), “Illusory correlations” (a belief that there exists a correlation where there is none, such that a certain person or item is associated with winning), “Availability of others’ wins” (overestimating the likelihood of winning based on others wins), “Inherent memory bias” (tendency to remember wins over losses), “Illusion of control” (overestimating the amount of control one has over random events) and “Switching and double switching” (losing an otherwise present ability to think rationally when gambling). In another review by Leonard et al. (2015) six specific distortions were identified, of which some overlapped with the distortions identified by Fortune and Goodie (2012). Leonard et al. (2015) identified the “Gamblers’ fallacy”, “Illusion of control”, and the “Belief that luck is dispositional “ (which largely corresponds to Illusory correlations) and in addition they also identified “Base rate neglect” (overestimating the general frequency of certain events, like winning the lottery), “Insensitivity to sample size” (tendency to extrapolate outcomes from small samples), and the “Hot hand fallacy” (believing that a winning streak portends more winning even when the outcome is random). These distortions are present among both non-problem and problem gamblers, and there are marked heterogeneity between individuals in the respective groups (Leonard & Williams, 2016). Even so, cognitive distortions have been implicated in maintaining problem and pathological gambling (Fortune & Goodie, 2012). It has been shown that pathological and problem gamblers are more inclined to endorse cognitive distortions compared to non-pathological gamblers, social gamblers and non-gamblers (Joukhador et al., 2003; MacKillop et al., 2006a; Myrseth et al., 2010; Xian et al., 2008). It has also been found that cognitive distortions are a predictor for relapse in members of Gamblers Anonymous (Oei & Gordon, 2008) and for the development of future gambling problems among current non-problem gamblers (Leonard & Williams, 2016). Some success has even been shown with cognitive therapy for gambling focusing on correcting cognitive distortions and giving information about relapse prevention techniques as the only treatment components (Ladouceur et al., 2001, 2003). Due to the important role of these cognitive distortions, and the focus on these in treatment, there is a need for valid instruments that can accurately measure them.

Several instruments have been developed to measure cognitive distortions in gamblers. The Gamblers’ beliefs questionnaire (GBQ; Steenbergh et al., 2002), the Informational biases scale (IBS; Jefferson & Nicki 2003), the Perceived personal luck scale (PPLS; Wohl et al., 2005), the Gambling Related Cognition scale (GRCS; Raylu & Oei, 2004), the Gambling attitudes and beliefs survey (GABS; Breen & Zuckerman, 1999), and the Video gaming device inventory (VGDI; Pike, 2002) are all examples of such instruments (for a review see Fortune & Goodie, 2012; Leonard et al., 2015). To our knowledge there is only one such instrument available in Swedish, called “Tankar om spel”. This instrument has been used in two studies (Jonsson et al., 2003; Källmen et al., 2008;) to compare cognitive distortions between non-problem and problem gamblers. We have however not found any validation study of this instrument and so its psychometric properties are not fully known. However, one internationally published instrument that has shown good psychometric properties is the Gamblers’ Beliefs Questionnaire (GBQ) (Goodie & Fortune, 2013; MacKillop et al., 2006b; Mattson et al., 2008; Mitrovic & Brown, 2009; Philander et al., 2019). In a meta-analysis by Goodie and Fortune (2013) the GBQ was found to have been investigated in the most extensive number of studies, with a large collective N coming from different laboratories with a large effect size and a narrow 95% CI.

The GBQ has also been demonstrated to be sensitive to treatment in disordered gamblers (Winfree et al., 2015) and for prevention with at-risk gamblers (Doiron & Nicki, 2007). Winfree et al. (2015) showed that in a sample of treatment seeking gamblers, GBQ scores were significantly lower one month after completion of a 5–8 week CBT treatment program than at pre-treatment. Doiron and Nicki (2007) further showed that a group of at-risk video lottery terminal gamblers given a prevention program had significantly lower cognitive distortions as measured by the GBQ at post-treatment and at a one month follow-up compared to a wait-list control.

Originally the GBQ consisted of 21 items (Steenbergh et al., 2002) in which respondents rate their level of agreement on a seven point likert scale from 1 (strongly agree) to 7 (strongly disagree). The Steenbergh et al. (2002) consisted of five different studies from a sample of community members and undergraduate students (n = 403). An explorative factor analysis revealed two underlying factors, Luck/Perseverance and Illusion of Control. The GBQ also demonstrated excellent internal consistency (α = 0.92) and adequate test–retest reliability (r = 0.77). The internal consistency within the two subscales was, Luck/Perseverance (α = 0.90) and Illusion of Control (α = 0.84) respectively. Internal consistency reflects to which extent the different items of an instrument measure aspects of the same construct (Revicki, 2014). Test–retest reliability reflects the stability of test-scores when measuring the same characteristic on different occasions (Vilagut, 2014). Further, it was found that problem and pathological gamblers showed more cognitive distortions as assessed by the GBQ than non-problem gamblers. Higher scores on the GBQ also correlated positively with amount of time spent gambling, as did factor Luck/Perseverance. No such association was found with factor Illusion of control (Steenbergh et al., 2002). The GBQ was later changed into a 20-item version by the original authors (Winfree et al., 2013) based on item content consideration. It is this 20-item version that is used in our translation. The GBQ 20-item, was first translated into Spanish (Winfree et al., 2013). In a sample of community members (n = 219) an exploratory factor analysis was performed, and the same factors was found as in the original article, but with somewhat different factor loadings. Based on this the two subscales were retained but with minor item changes, Luck/Perseverance (items 5, 7, 11–20) and Illusion of control (items 1–4, 6, 8–10). The Spanish translation of the 20-item version has shown good psychometric properties. Internal consistency for the whole scale was (α = 0.95), and for factor Luck/Perseverance (α = 0.96), and factor Illusion of Control (α = 0.86). Positive correlations were found with instruments measuring problem gambling severity, also pathological gamblers showed more cognitive distortions than non-gamblers and non-pathological gamblers (Winfree et al., 2013).

Besides the Spanish translation of the GBQ, the original 21 item GBQ has been translated and validated into Chinese (Wong & Tsang, 2012) and Italian (Marchetti et al., 2016). The translated versions of the GBQ has demonstrated to be reliable by showing excellent (Cicchetti, 1994) internal consistency (Wong & Tsang, 2012; Winfree et al., 2013; Marchetti et al., 2016) and adequate test–retest reliability (Marchetti et al., 2016).

There is also evidence for construct validity of the translated instruments, meaning that they measure the theoretical trait they are supposed to (Ginty, 2013). This has been done by demonstrating two subtypes of construct validity: convergent validity and known-groups validity. Convergent validity supports the validity of the construct by showing that it is correlated to other constructs to which it is conceptually similar (Chin & Yao, 2014). Convergent validity of the GBQ has been demonstrated by medium (Cohen, 1988) relationships with instruments measuring gambling problems (Winfree et al., 2013; Marchetti et al., 2016) and large relationships with an instrument measuring gambling urges and another instrument measuring cognitive distortions related to gambling (Wong & Tsang, 2012). Known-groups validity is demonstrated when an instrument can discriminate between two groups known or assumed to differ on the construct the instrument is supposed to measure (Davidson, 2014). Known-groups validity has been demonstrated by finding significant differences in levels of cognitive distortions as measured by the GBQ between problem- and pathological gamblers and non-gamblers (Winfree et al., 2013; Marchetti et al., 2016).

Unfortunately, there have been some conflicting results regarding the subscales Luck/Perseverance and Illusion of Control. In the original study by Steenbergh et al. (2002) an exploratory factor analysis found two underlying factors, labeled Luck/Perseverance and Illusion of Control. This result was replicated with the Spanish translation by Winfree et al. (2013) and confirmed via a confirmatory factor analysis in a population of Argentinian gamblers (Pilatti et al., 2016). A confirmatory factor analysis is a statistical procedure that tests how well the measured variables (in this case the separate items of the GBQ) represent the number of hypothesized constructs (in this case the two factors of Luck/Perseverance and Illusion of Control). However, the Chinese translation (Wong & Tsang, 2012) failed to find support for the original two-factor structure via confirmatory factor analysis. For the Italian translation (Marchetti et al., 2016) an exploratory factor analysis also failed to replicate the two-factor model. Although Winfree et al. (2013) managed to replicate the results of the original study, they found that several items loaded similarly on the two different factors and suggested these items could be excluded from the instrument for a purer measure of the factors of Luck/Perseverance and Illusion of Control. Later, both Winfree et al. (2015) and Philander et al. (2019) has failed to find support for the two-facture structure in the 20-item English version. Still, even though there are conflicting results regarding the subscales, the full GBQ can be considered a valid and reliable instrument for measuring general gambling related cognitive distortions (Winfree et al., 2013) as the results regarding the full GBQ has been consistent in all versions so far (Steenbergh et al., 2002; Wong & Tsang, 2012; Winfree et al., 2013; Marchetti et al., 2016).

Even though the GBQ has a few psychometric shortcomings we have chosen to translate and validate the instrument to Swedish based on the extensive work previously made by other researchers (Wong & Tsang, 2012; Winfree et al., 2013; Pilatti et al., 2016; Marchetti et al., 2016; Philander et al., 2019) and the sensitivity to treatment shown by the GBQ in a treatment seeking population (Winfree et al., 2015). There is a great need in Sweden for an instrument like the GBQ that validly measure cognitive distortions related to gambling, both for use in case conceptualization and as an outcome measure. The aim of this study is therefore to translate the GBQ to Swedish and validate it in a Swedish cultural context.

Based on results of previous validations our primary hypothesis is that we will find evidence for the reliability and validity of our translation (GBQ-SE). In more detail, we expect that it will demonstrate 1) at minimum good internal consistency for the full scale and subscales 2) a medium strong relationship (r = 0.30—0.50) of the full scale and subscales with instruments measuring gambling problem severity (convergent validity) and 3) that problem gamblers will show significantly higher scores on the GBQ-SE than non-problem gamblers (known-groups validity). Secondary, as there is conflicting evidence as to the two-factor structure we will assess if the two-factor structure is confirmable in the Swedish translation. We will also explore the internal validity and scaling success of the GBQ-SE.

Method

Participants

Two groups of participants were recruited with a purposive sampling method (Shadish et al., 2002; Winfree et al., 2013). One group, chosen to represent a cross section of the Swedish population, was found in workplaces, sports associations and at the university. The other group was chosen from a self-help group for former or current pathological gamblers and also from a clinic that treats pathological gamblers. This was to ensure that enough participants with current or historic gambling problems were included in the validation.

The eligibility criteria were 18 years of age and being fluent in Swedish. Participants included a total of n = 438 adults and of these 172 were university students (39%), 184 were recruited at workplaces or sports associations (42%) and 82 had a possible experience of current or historic problem gambling (19%). Thirty-six participants declined to participate or answered the questionnaires incompletely in such a way that they were not possible to include in the analysis (see section Missing data). A total of n = 402 were therefore included in the analysis. Demographic data is summarized in Table 1.

Table 1 Demographics of total sample, non-problem gamblers and problem gamblers. Data are presented as means and standard deviations M (SD) and in percent (%)
Full size table

Study Design and Procedure

Participant recruitment and data collection was done between June and October 2019. The study consisted of recruiting participants to directly answer a questionnaire packet consisting of a short demographic questionnaire, the GBQ-SE, and two standardized measures of gambling severity (PGSI and NODS, see below). The experimenters approached participants at group gatherings, at work places, sports associations and self-help groups. The objectives of the study were explained and that the study, in abidance to national ethics, were completely anonymous in nature. Participants were handed a pencil and the questionnaire packet, which they could choose to fill in, or leave blank if choosing not to participate. The packets were then collected and put into storage to ensure no possibility for the experimenters to know who agreed to participate or not. The participants that were patients at the clinic for pathological gamblers received written information about the study from their counselors. This information had the same content as the information given to the other participants. They were then handed the questionnaire packet and an unsealed envelope. They could choose to fill in the questionnaires, or leave them blank if declining to participate. In either case they sealed the envelopes and handed them back to their counselors, to ensure total anonymity.

Measures

Participants were screened for gambling problems using two standardized self-report questionnaires commonly used in Sweden. All questionnaires were used in a version translated to Swedish. In addition, a few demographic variables were also taken.

Demographics and Gambling Participation

This short questionnaire assessed participants’ age in years, gender, education and marital status. They were also asked if they had participated in any kind of gambling over the last 12 months.

The Gamblers’ Beliefs Questionnaire – Swedish (GBQ-SE)

The Swedish translation of the 20-item GBQ.

The NORC Diagnostic Screen for Gambling Problems (NODS)

The NODS is a 17 item self-report questionnaire for assessment of gambling problems (Wickwire et al., 2008). The items consist of yes/no questions and scores can be classified into one of four categories: no gambling problems, risk gambling, problem gambling and pathological gambling. The NODS come in several versions: lifetime, past 12-months and past 30 days. The current study used the lifetime version of the NODS to assess lifetime gambling problems. NODS lifetime has shown good internal consistency (α = 0.88) and adequate levels of concurrent and discriminant validity (Wickwire et al., 2008). Excellent internal consistency (α = 0.98) was demonstrated with the sample in this study.

Problem Gambling Severity Index (PGSI)

PGSI is a nine-item screening instrument assessing the degree of gambling problems during the last 12 months (Ferris & Wynne, 2001). Respondents answer by indicating how often the statements are correct on a four point scale from”never” to”almost always”. Scores range from 0–27 and are classified into four different categories: 0 = non-problem gambler, 1–2 = low risk gambler, 3–7 = moderate risk gambler, 8 +  = problem gambler. PGSI has demonstrated good internal consistency (α = 0.84) and good concurrent validity (Ferris & Wynne, 2001). Excellent internal consistency (α = 0.97) was demonstrated with the sample in this study.

Translation

The GBQ-SE was translated into Swedish with back-translation methodology (Brislin, 1970). The team of translators consisted of four people. The first author, a doctoral student, made the translation from English into Swedish. It was then checked and discussed together with the last author who is an associated Professor. Together they corrected linguistic and grammatical errors. Then, two bilingual individuals with English as a native tongue, made two separate back-translations from the Swedish version back to English. The first and last authors then examined consistency between the original version and the back-translated versions. Some final modifications were made of the GBQ-SE in order to retain the meaning of the English original scale.

Data Analysis

Analysis was for the majority of analyses run on IBM SPSS Statistics version 25. The confirmatory factor analysis was run on SAS version 9.4. The analysis plan was created in consultation with a statistician. Data was removed from the”Demographics and gambling participation”-questionnaire in cases when participants had only completed this questionnaire and therefore were not part of any analysis. Data was removed from NODS and from the PGSI if one or more items contributing to the final score were missing. For the GBQ-SE data was removed for participants if more than two of the items were missing. If two or fewer items were missing the participants mean item-score for completed items were calculated and substituted for the missing item (Downey & King, 1998). After missing data procedures were completed a total of n = 402 participants were in included in the analysis. Data used for analyses for the different instruments were: GBQ-SE (n = 397), NODS (n = 391), PGSI (n = 394). Frequency of missing data was between 9–11% based on the total number of participants (n = 438).

For testing normality of the data from the full GBQ-SE and its subscales Luck/Perseverance and Illusion of Control as well as for the NODS and PGSI a Shapiro-Wilks test were used (Razali & Wah, 2011; Shapiro & Wilk, 1965). An indication of non-normality was found (p < 0.001) and a further descriptive analysis showed that the data was positively skewed for all scales and subscales mentioned above. Differences in scores of gambling severity as measured by the NODS and PGSI between problem gamblers and non-problem gamblers were assessed using Mann–Whitney U tests due to the non-normality of the data. In this study a cut-off score of three on the PGSI was used to categorize problem gambling. This approach was used as the prevalence is low for a PGSI cut-point of 8 points or above (Stone et al., 2015). A common approach to address this is by merging the PGSI moderate-risk and problem gambler groups to create a lower threshold cut-off score of three points (Afifi et al., 2010; Crockford et al., 2008; Stone et al., 2015).

In order to assess internal consistency of the GBQ-SE and subscales Luck/Perseverance and Illusion of Control coefficient alpha (Cronbach, 1951) was calculated. Convergent validity of the GBQ-SE was assessed by a correlation analysis between instruments measuring gambling problem severity (NODS, PGSI) and the full GBQ-SE and subscales. Due to the data not being normally distributed Spearman’s rank-order correlation coefficient were used. In order to assess known-groups validity, differences between non-problem gamblers and problem gamblers on GBQ-SE scores were tested. Due to the non-normality of the data distribution Mann–Whitney U tests were used here. The term known-group validity is not used in other GBQ studies (Steenbergh et al., 2002; Winfree et al., 2013; Marchetti et al., 2016) when describing these procedures, but we chose to use the term to be more specific as to which subtype of construct validity we investigated. In order to assess if the two-factor structure of the 20 item GBQ found in Winfree et al. (2013) and confirmed in Pilatti et al. (2016) was confirmable in our sample, a confirmatory factor analysis was performed for the two-factor model. As the data was not normally distributed the Robust Maximum Likelihood Estimation was used to adapt the model in the confirmatory factor analysis as it allows non-normal data (Brown, 2015). The internal validity of the GBQ-SE was explored by assessing item convergent validity, item discriminant validity and scaling success. Item convergent validity of GBQ-SE and its subscales were assessed by correlating each item to its own scale corrected for overlap using Pearson’s product moment correlation coefficient. Item discriminant validity was assessed by correlating each item in either subscale to the other subscale. Pearson’s product moment correlation coefficient was used for this analysis. Scaling success was determined by for each item calculating if correlations were significantly higher (p < 0.05) to the own subscale compared to the other subscale. In order to compare correlations they were transformed to z-values using Fishers r – z transformation.

Results

Gambling Behavior Measured By The NODS and PGSI

Descriptive analyses showed that the level of gambling problems in the total sample measured by the NODS were M = 1.55, SD = 3.29 (n = 391) and on the PGSI it was M = 1.49, SD = 4.75 (n = 394). The sample was comprised of n = 350 non-problem gamblers (88.8%) and n = 44 problem gamblers (11.2%). A first Mann–Whitney test revealed significantly lower levels of gambling problems as indicated by the NODS in non-problem gamblers, M = 0.71, SD = 2.26, n = 343 than in problem gamblers M = 8.26, SD = 2.51 n = 43, U = 14,175.5, p < 0.001, r = 0.66. A second Mann–Whitney test also showed that non-problem gamblers scored less on the PGSI than problem gamblers did. Non-problem gamblers reported a mean score of M = 0.05, SD = 0.26, n = 350 and problem gamblers M = 12.98, SD = 7.33, n = 44, U = 15,400, p < 0.001, r = 0.90. For a summary of means and standard deviations for NODS, PGSI and the GBQ see Table 2.

Table 2 Means and standard deviations M (SD) of the GBQ-SE, NODS and PGSI for total sample, non-problem gamblers and problem gamblers
Full size table

The Gamblers’ Beliefs Questionnaire – Swedish

Internal consistency was assessed by calculating coefficient alpha (Cronbach, 1951) and was found excellent for the full GBQ-SE (α = 0.94) and factor Luck/Perseverance (α = 0.92), and good for factor Illusion of Control (α = 0.86) (Cicchetti, 1994).

In order to assess convergent validity, the relationships between the GBQ-SE and its subscales, and the severity of gambling problems assessed by NODS and PGSI, were examined using Spearman’s rho correlation coefficient. As expected, there were significant medium strong positive relationships between the full scale GBQ-SE and both NODS and PGSI. GBQ-SE to NODS, rs = 0.42, p < 0.001, GBQ-SE to PGSI, rs = 0.42, p < 0.001. The subscales Luck/Perseverance and Illusion of Control also showed medium strong positive relationships with NODS and PGSI. Luck/Perseverance to NODS, rs = 0.42, p < 0.001, Luck/Perseverance to PGSI, rs = 0.43, p < 0.001, Illusion of Control to NODS, rs = 0.36, p < 0.001, Illusion of Control to PGSI, rs = 0.35, p < 0.001. See Table 3 for correlation coefficients, expected correlation coefficients and confidence intervals.

Table 3 Expected and actual correlations for convergent validity of the GBQ-SE
Full size table

Known-groups validity was assessed by examining if scores on the GBQ-SE and its subscales differed between non-problem gamblers and problem gamblers as defined by the PGSI. A Mann–Whitney test revealed that problem gamblers (n = 44) scored significantly higher on the GBQ-SE (M = 72.34, SD = 25.19) than non-problem gamblers (n = 345) (M = 40.21, SD = 18.12, n = 345) U = 12,858, p < 0.001, r = 0.38. The same was found for factor Luck/Perseverance, problem gamblers (M = 41.86, SD = 18.16), non-problem gamblers (M = 20.00, SD = 10.41) U = 12,917, p < 0.001, r = 0.39, and factor Illusion of Control, problem gamblers (M = 30.48, SD = 9.21), non-problem gamblers (M = 20.22, SD = 9.31) U = 11,871, p < 0.001, r = 0.31 (see Table 2).

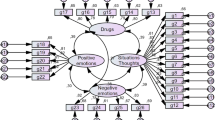
To assess if the two-factor model of Luck/Perseverance and Illusion of Control found in Winfree et al. (2013) and confirmed in Pilatti et al. (2016) was valid in this dataset, a confirmatory factor analysis was performed. The Robust Maximum Likelihood Estimation was used to adapt the model. See Table 4 for standardized factor loadings. A Chi-square test was performed to see if the observed variance matrix was statistically different from the estimated variance matrix, Χ2 (169, 397) = 694.77, p < 0.001. A significant result rejects the hypothesis that the observed result is similar to the estimated result (Brown, 2015) and thus indicate that the data does not fit the model. In addition, four different indicators of fit are reported: the Standardized Root Mean Residual (SRMR), the Root Mean Square Error of Approximation (RMSEA), Bentlers Comparative Fit Index (CFI), and the Tucker-Lewis index (TLI). The SRMR is the square root of the average discrepancy between the correlations observed in the input matrix and the correlations predicted by the model. The RMSEA is an “error of approximation” index and thus assess the extent to which the model fits the data reasonably well. The CFI and the TLI evaluates the fit of the model compared to the fit of a null model (Brown, 2015). SRMR = 0.065, a value close to or below 0.08 indicate a good fit between the model and the observed data. RMSEA = 0.089 (90% CI, 0.082—0.096), a value close to 0.06 or below indicate good fit, whereas a value between 0.08—0.10 suggests a mediocre fit. CFI = 0.90, TLI = 0.88 a value of 0.95 indicate good fit whereas a value of 0.90—0.95 indicate acceptable fit for both indicators (Brown, 2015). As can be seen the results are mixed, but together they indicate a slightly below acceptable fit of the model to the data.

Table 4 Standardized factor loadings for GBQ-SE
Full size table

Item convergent and discriminant validity, as well as scaling success were assessed by correlating each item to its own subscale (item convergent validity) and to the other subscale (item discriminant validity) and for each item test if the correlation was significantly higher to its own scale than to the other scale (scaling success), see Table 5. The Pearson correlations for items 7, 11, 14 and 16 in the subscale Luck/Perseverance were not higher to its own scale, ns. Pearson correlations for items 1, 2 6, and 10 in factor Illusion of Control were not higher to its own scale, ns.

Table 5 Internal validity as demonstrated by item convergent and discriminant validity, and scaling success for GBQ-SE, factor Luck/Perseverance and factor Illusion of Control
Full size table

Conclusions

In this study we translated the GBQ, a commonly used instrument for measuring cognitive distortions related to gambling, to Swedish and found initial evidence for reliability and validity of the instrument. First, the translation was successful, with the GBQ-SE items retaining the meaning of the items from the original scale. Second, internal consistency was found to be excellent for the whole GBQ-SE and the Luck/Perseverance subscale, and good for the Illusion of Control subscale. Third, convergent validity was demonstrated with two different instruments measuring gambling problem severity, the NODS and the PGSI. A medium strong relationship was found between both instruments and the GBQ-SE. Fourth, problem gamblers, defined by the PGSI, scored significantly higher with medium sized effects on the GBQ-SE and its subscales compared to non-problem gamblers, demonstrating known-groups validity. Fifth, a confirmatory factor analysis barely failed to show an acceptable fit between the two-factor model and the data. Finally, when assessing internal validity and scaling success a total of eight out of 20 items did not show a significantly stronger relationship with its own subscale than with the other subscale indicating some overlap between the two subscales.

Considering the translation process, a back-translation protocol was employed successfully. In similarity with both the Spanish (Winfree et al., 2013) and the Italian (Marchetti et al., 2016) translations a number of English gambling-related terms could not be direct translated and had to be approximated, or slightly reworded, in order to capture the meaning of the original scale. We also chose to retain the English terms “bet” and “betting” since the English words are commonly used in Sweden in the context of gambling. We believe these changes helped retain the meaning of each item from the original scale. Even with these small adjustments to the Swedish language the GBQ-SE items kept the meaning from the original scale and generated an appropriate translation.

Regarding internal consistency, the GBQ-SE showed excellent internal consistency (α = 0.94) for the full scale and the luck/perseverance subscale (α = 0.92), and good internal consistency (α = 0.86) for the illusion of control subscale. Internal consistency reflects the degree to which items in a scale measure the same underlying construct (Revicki, 2014). It is in this way a measure of reliability, as high internal consistency reflects a lower rate of random measurement error (Viswanathan, 2005). The excellent internal consistency found in this study therefore provides support for the reliability of the GBQ-SE. Moreover, our findings were consistent with the original GBQ (Steenbergh et al., 2002) (full scale α = 0.92; luck/perseverance α = 0.90; Illusion of Control α = 0.84), the Chinese GBQ-C (full scale α = 0.91; luck/perseverance α = 0.86; Illusion of Control α = 0.82) (Wong & Tsang, 2012), the Spanish GBQ-S (full scale α = 0.95; luck/perseverance α = 0.96; Illusion of Control α = 0.86) (Winfree et al., 2013) and the Italian GBQ-I (full scale α = 0.93) (Marchetti et al., 2016), with internal consistencies only differing by a few points from each other. The similarity with previous studies further supports that our translation process was successful. It might also reflect that the construct being measured by the GBQ is similar across different languages and cultures.

To assess convergent validity, we tested if participants severity of gambling problems measured by both the NODS and the PGSI were related to the reported gambling-related cognitive distortions on the GBQ-SE. The correlations found were medium strong (GBQ-SE to NODS rs = 0.42; GBQ-SE to PGSI rs = 0.42; Luck/Perseverance to NODS rs = 0.42; Luck/Perseverance to PGSI rs = 0.43; Illusion of Control to NODS rs = 0.36; Illusion of Control to PGSI rs = 0.35). This provides support for the validity of the instrument as it is related to a conceptually associated construct. Similar results were found when examining the relationship between the GBQ and gambling problem severity measured with the South Oaks Gambling Screening instrument (SOGS; Lesieur & Blume, 1987) for both the Spanish (r = 0.33) (Winfree et al., 2013) and the Italian (r = 0.43) (Marchetti et al. 2016) translations. Our results were also largely consistent with studies where the English versions of the GBQ have been correlated to instruments measuring gambling severity, in where the strengths of relationships has ranged from small to medium (MacKillop et al., 2006b; Mattson et al., 2008; Mitrovic & Brown, 2009; Winfree et al., 2015). The similarity with other versions of the GBQ provides further evidence that our translation was successful. Our results also further strengthen the evidence that cognitive distortions related to gambling are positively associated with gambling problems and that this is true in different languages and cultures. The small to medium relationships between cognitive distortions and gambling severity that were found in all studies where the GBQ have been used is theoretically consistent. This is due to that gambling related cognitive distortions are more common with more severe gambling problems but still exists among all gamblers and is heterogeneous between individuals (Leonard & Williams, 2016).

In order to explore known-groups validity the difference in GBQ-SE scores between non-problem gamblers and problem gamblers were tested. Problem gamblers were found to score higher on the full GBQ as well as on the subscales Luck/Perseverance and Illusion of Control. The differences were all significant and medium sized. This means that our translation was successful in discriminating between non-problem and problem gamblers, replicating the results of earlier studies. In the original validation by Steenbergh et al. (2002) they found that pathological gamblers identified by DSM-IV criteria and problem and pathological gamblers identified by the SOGS scored significantly higher than non-pathological gamblers, with a large effect size for pathological gamblers identified by the DSM-IV and a medium effect size for those identified by the SOGS. In the Spanish translations of the GBQ it was found that pathological gamblers, likewise identified by the SOGS and also with the DSM-IV criteria, scored significantly higher on the GBQ than both non-gamblers and non-pathological gamblers did, with a large difference (Winfree et al., 2013). Further, Marchetti et al. (2016) also found that their translation of the GBQ was sensitive to discriminate between non-gamblers, social gamblers and probable problem/pathological gamblers as measured by the SOGS, with a large effect size. The relative size of the differences varies between different studies, and this might partially be due to the way in which problem gamblers were defined. In our study we used a low cut-off score of three on the PGSI to define the problem gambler group as the original cut-off of eight has shown a low prevalence of problem gamblers (Stone et al., 2015). Using a cut-off score of three is a common way to address this problem (Afifi et al., 2010; Crockford et al., 2008; Stone et al., 2015). Williams and Volberg (2014) have shown that a cut-off score of five was most accurate compared to assessments made in clinical interviews. Perhaps using a cut-off of five in this study would have better captured the problem gambler group. Indeed, the cut-off score of three in this study captured a number of participants that had not gambled at all over the past 12 months. This is possible due to some questions in the PGSI asking about indirect consequences of gambling, such as emotional or financial problems, and it is possible to still have these problems even though you have not gambled lately. Even though the GBQ successfully discriminates between problem gamblers and non-problem gamblers, it’s not a normative scale and one must not forget that it does not provide an alternative for a diagnosis of pathological gambling. It does however provide a way for clinicians and researchers to be able to detect and measure cognitive distortions in gamblers.

The confirmatory factor analysis used to assess the validity of the two-factor model could not confirm an acceptable fit between the model and the data. It was however quite close to an acceptable but mediocre fit. Of the three other studies in where a confirmatory factor analysis was performed on the 20-item GBQ, two failed (Philander et al., 2019; Winfree et al., 2015) and one succeeded (Pilatti et al., 2016). When comparing the results they are however quite close to each other. Winfree et al (2015) reported SRMR = 0.096, RMSEA = 0.095, CFI = 0.76. Pilatti et al. (2016) reported RMSEA = 0.085, CFI = 0.92, TLI = 0.90. Philander et al. (2019) reported RMSEA = 0.11, CFI = 0.89, TLI = 0.88. This can be compared to our results of SRMR = 0.065, RMSEA = 0.089, CFI = 0.90, TLI = 0.88. Especially the results from our study are quite close to both the study by Philander et al. (2019) and by Pilatti et al. (2016), even when the results lie on different sides of the suggested cut-offs. This might indicate that the two-factor model overall is close to an acceptable fit to the data, and that small variations in the dataset and study sample size is enough to affect if the model is deemed acceptable or not. This might explain the varying results of confirmatory factor analyses in the different validation studies of the GBQ to date. Even so, based on the result of our and previous studies, it is not possible to be fully confident in the two-factor model of the GBQ.

When assessing internal validity and scaling success we found that four items in the subscale Luck/Perseverance and four in factor Illusion of Control overlapped i.e. they did not correlate more strongly to their own scale than to the other scale. This result did not come as a surprise to us as earlier exploratory factor analyses have shown some items to have similar factor loadings in both factors (Steenbergh et al., 2002; Winfree et al., 2013). The results are hard to compare with the results of the original study (Steenbergh et al., 2002) as it was done on the 21-item version of the GBQ. It is however possible to compare it to the Spanish translation (Winfree et al., 2013) as it also uses the 20-item GBQ. In the exploratory factor analysis of the Spanish translation they found similar factor loadings on four items. We found in our study that three of these items had similar correlations to both subscales. In addition we also found another five items that did not discriminate properly between subscales. Even if more items proved to be associated to both subscales in our study, there is still a similarity regarding which items did not clearly discriminate between the two subscales. The results from our study, as well as from Steenberg et al. (2002) and Winfree et al. (2013) indicate that there is overlap between the two subscales. This is interesting since our study, and several earlier studies have not been able to replicate or confirm the two-factor structure of the GBQ (Wong & Tsang, 2012; Winfree et al., 2015; Marchetti et al. 2016) and overlap between the subscales might be an explanation for this. A possible explanation for this overlap is that the items that do not properly discriminate between the subscales are measuring aspects of both constructs. This seems likely considering the content of these items. As argued by Philander et al. (2019) it is also possible that the constructs represented by the two subscales aren’t fully independent from each other or are related to a wider cognitive distortion. Even so, the current version of the GBQ-SE should be useful as an instrument measuring general cognitive distortions related to gambling. By replicating the results for internal consistency, convergent validity and known-groups validity from other validation studies, this study provides general support for the GBQ as a useful instrument in different languages and cultures, and more specifically for the reliability and validity of the Swedish translation. However, in unison with Winfree et al. (2013) and Philander et al. (2019), if a more distinct measure of the underlying constructs is wanted we suggest excluding the overlapping items, effectively constructing a shorter version of the GBQ. The fact that this study could not confirm the two-factor model, as well as the clear overlap between the two subscales in the current version, cautions against interpreting the subscales by themselves.

This study has several strengths but also limitations. The main strength of the study is that we replicated other validation studies on the GBQ in a Swedish cultural context. Another strength is that by analyzing internal validity and scaling success and finding that eight out of 20 items showed similar correlations with both subscales of Luck/Perseverance and Illusion of Control we brought further light onto earlier difficulties of confirming the two-factor model. Furthermore this study strengthened the evidence that problem gamblers tend to endorse more gambling related distortions than non-problem gamblers, by finding a significantly higher level of cognitive distortions in the problem gambler group. There are however also a number of limitations with the current study. First there was missing data for NODS, PGSI and the GBQ-SE reducing the sample size with approximately 10%. Secondly, there were relatively few participants with problematic gambling in the sample which made it impossible to further differentiate this group in the analysis, for example by splitting the problem gambler group into pathological gamblers and problem gamblers and analyze them separately. A larger overall sample size could have made a more differentiated analysis possible. Third, the data was skewed, thus violating the assumptions for parametric statistics. The skewness of the data is however expected due to the relatively low prevalence of gambling problems in the general population. Fourth, due to the anonymous nature of the study it was not possible to assess the test–retest reliability of the GBQ-SE in this study, as participants could not be identified and asked to complete the questionnaire packet again at a later time. Finally, the sample consisted mostly of members of the general population as well as a smaller number of participants with known current or historical gambling problems. It is therefore not clear how the results generalize to other groups, such as various gambler subgroups.

A general weakness with the GBQ, as well as many other instruments that measure gambling related cognitive distortions is that it also contains items that are typically more about gambling behavior, thoughts or feelings, and not cognitive distortions per se (Leonard et al., 2015). For example, item 13 “If I lose money gambling, I should try to win it back” reflects a typical behavior among disordered gamblers, rather than a specific distortion. These kinds of items risk to inflate correlations with instruments measuring gambling problems, as such instruments often have similar items (Leonard et al., 2015). However, even with this weakness the GBQ is still one of the most proven instruments of general gambling related cognitive distortions, with good psychometric properties.

Several areas are of interest for future research. The current version of the GBQ-SE should be tested in different subgroups, and its temporal stability should be assessed. To make the instrument more clinically useful, future studies should try to identify what is to be considered a problematic level of cognitive distortions and establish cut-off scores that could be used for clinical interpretation. It has previously been shown that the instrument is sensitive to treatment (Winfree et al., 2015) but it would be valuable to also demonstrate this in a Swedish cultural context. As discussed earlier, if a more distinctive measure of the particular cognitive distortions of Illusion of Control and Luck/Perseverance are wanted, a more condensed version of the GBQ-SE could be created and further validated.

In summary we investigated the validity of a Swedish translation of the GBQ, an instrument created to assist in case conceptualization, treatment planning, cognitive restructuring and as an outcome measure during treatment of problem- and pathological gamblers. The current study found initial evidence for the viability of this Swedish translation as a general instrument measuring cognitive distortions related to gambling, replicating the results of previous validation studies in other languages. We were however unable to confirm the two-factor model, and in addition to this we found a clear overlap between the two subscales, which cautions against interpreting these by themselves. Even with the limitations of the GBQ-SE we believe it is useful as a general instrument measuring cognitive distortions related to gambling, and it is the first such instrument in Swedish to have undergone a validation procedure. More research is needed to make it more clinically interpretable, but clinicians can still use it as a means to assess what types of thoughts their clients entertain, and thus aid in cognitive restructuring and case conceptualization. It can also be used for research purposes, for example to evaluate treatment outcome. Indeed the Banff consensus for reporting outcomes in problem gambling treatment research establishes the need for evaluating supposed active treatment processes (Walker et al., 2006). One such process in CBT is changing the clients erroneous beliefs regarding gambling.