Abstract
The niche and fitness differences of modern coexistence theory separate mechanisms into stabilizing and equalizing components. Although this decomposition can help us predict and understand species coexistence, the extent to which mechanistic inference is sensitive to the method used to partition niche and fitness differences remains unclear. We apply two alternative methods to assess niche and fitness differences to four well-known community models. We show that because standard methods based on linear approximations do not capture the full community dynamics, they can sometimes lead to incorrect predictions of coexistence and misleading interpretations of stabilizing and equalizing mechanisms. Specifically, they fail when both species occupy the same niche or in the presence of positive frequency dependence. Conversely, a more recently developed method to decompose niche and fitness differences, which accounts for the full non-linear dynamics of competition, consistently identifies the correct contribution of stabilizing and equalizing components. This approach further reveals that when the true complexity of the system is taken into account, essentially all mechanisms comprise both stabilizing and equalizing components and that local maxima and minima of stabilizing and equalizing mechanisms exist. Amidst growing interest in the role of non-additive and higher order interactions in regulating species coexistence, we propose that the effective decomposition of niche and fitness differences will become increasingly reliant on methods that account for the inherent non-linearity of community dynamics.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Niche and fitness differences are two central concepts in coexistence theory which help us to understand species coexistence. Whether or not species coexist depends on how much species limit each other’s growth compared to their own growth. From a mechanistic standpoint, various factors, such as resources (Letten et al. 2017), predators (Chesson and Kuang 2008; Holt et al. 1994) or mutualists (Johnson 2021), can limit population growth. Population sizes will in turn influence these factors (Meszena et al. 2006) (e.g., by depleting resources or by boosting the population size of their predators), as such creating the regulating feedback underpinning growth limitation. Thus, mechanistically, niche differences (1- niche overlap) measure how independent the feedback loops of two species are. If the feedback loops are completely independent, then niche differences are 1, conversely, if all feedback loops, intra- and interspecific, are equivalent, niche differences are 0. Fitness differences measure the relative strength of the feedback loops. Species will coexist when niche differences overcome fitness differences (Adler et al. 2007; Chesson 2013).
Unfortunately, computing niche and fitness differences taking into account the full complexity of limiting factors is not a straightforward task. Some available methods therefore apply to simple models only (Spaak et al. 2022b), where the details of population regulation are omitted. One often applied method is to reformulate the equilibrium conditions of a two-species community model in linear terms, equivalent to the equilibrium conditions of a linear Lotka-Volterra model (Letten et al. 2017; Godoy et al. 2014; Johnson 2021; Spaak et al. 2022b). This writes the equilibrium competitor’s densities, which then act as limiting factors, in lieu of the actual factors that underpin species interactions. Often, this includes various assumptions on the time scales at which the limiting factors vary, as well as on the persistence of these factors (Letten et al. 2017; Johnson 2021; Chesson and Kuang 2008). While these simplifying assumptions will by design be violated in certain conditions, we do not know the implications of such violations for our capacity to understand coexistence. Such knowledge is important for application of coexistence theory, as is choosing the appropriate definition of niche and fitness difference (Godwin et al. 2020).
Here, we examine to what extent including non-linear characteristics of community models increases our understanding of coexistence. To this end, we assemble four community models, three of which explicitly model limiting factors, and one which considers direct non-linear effects of population density on per-capita growth. We rewrite the equilibrium conditions of all four models with linear functions and compare how the resulting niche and fitness differences differ from those of the full models including limiting factors and direct non-linear interactions. Based on this comparison, we first develop criteria to test whether the approximated models affect our ability to understand coexistence. Then, we graphically represent the assumptions made by the approximation method and show that these simplifications can result in large deviations in community dynamics, especially away from equilibrium. Importantly, we show that linear approximations of non-linear dynamics can sometimes result in the misunderstanding of community dynamics, e.g., positive niche differences even when both species occupy the same niche, and negative frequency dependence interpreted as positive frequency dependence and vice versa. Finally, we also show that accounting for the full non-linear dynamics of competition can yield new insights into the effects of mortality and resource availability on niche and fitness differences. Specifically, we find that changes in resource availability generally affect both niche and fitness differences, but additionally that local maxima and minima of niche and fitness differences exist.
Methods
Niche and fitness differences of four community models have so far been computed by analyzing the linear equilibrium conditions: Species competing for substitutable resources with a Holling type 1 response (Chesson 1990) and a Holling type 2 response (Letten et al. 2017), species competing for essential resources with a Holling type 2 response (Letten et al. 2017) and the annual plant model (Godoy and Levine 2014), see Table 1. For each of these models we used the niche and fitness differences (\(\mathcal {N}^A\;\text {and}\;\mathcal {A}^A\)) from the literature (Chesson 1990, 2013, 2018). The superscript A denotes their derivation from approximated models. To compute niche and fitness differences of the full model (\(\mathcal {N}^C\;\text {and}\;\mathcal {F}^C\)) we use the method outlined in Spaak and De Laender (2020). Spaak and De Laender (2020) have proposed this method based on theoretical considerations, which have since then been successfully used in phenomenological community models (Buche et al. 2022; Spaak et al. 2021; Spaak et al. 2022b), but we have little understanding whether this method gives conceptual correct interpretation for a mechanistic community model (Spaak et al. 2022a). The superscript C denotes their derivation from the full, non-linearized (complex) model. We will use \(\mathcal {N}\;\text {and}\;\mathcal {F}\) to denote niche and fitness differences based on any mathematical definition. All simulations and computations were done in Python 3.7.1 with NumPy version 1.15.4.
Niche and fitness differences based on approximated models
The computation of the approximated niche and fitness differences \(\mathcal {N}^A\;\text {and}\;\mathcal {F}^A\) is based on rearranging the equilibrium condition of a community model, given by \(\frac{1}{N_i}\frac{dN_i}{dt} = f_i(N_i,N_j) = 0\), into a form that is equivalent to the equilibrium condition of a Lotka-Volterra community model, given by:
where \(N_i\) is the density of species i, \(r_i\) is the intrinsic growth rate, \(\alpha _{ii}\) and \(\alpha _{ij}\) are the intra- and interspecific competition coefficients. This involves writing the parameters \(r_i, \alpha _{ij}\) and \(\alpha _{ii}\) of Eq. (1) as a function of the model parameters. Generally speaking, the linear approximations are chosen to match the zero net growth isoclines (ZNGI), i.e., \(f_i(N_i,N_j) = 0 \Leftrightarrow 1-\alpha _{ii}N_i-\alpha _{ij}N_j = 0\). Specifically, to compute the parameters of the approximation method one first sets \(r_i = f_i(0,0)\) to be the intrinsic growth rate. Second, to match the growth rates of each species at their monoculture equilibrium, i.e., \(f_i(\hat{N}_i^C,0) = 0\) one sets \(\alpha _{ii} = 1/\hat{N}_i^C\), where \(\hat{N}_i^C\) is the equilibrium density of species i in monoculture. Third, to match the growth rates of species i at the two-species equilibrium, i.e., \(f_i(N_i^*, N_j^*) = 0\), one sets \(\alpha _{ij}= \left( \hat{N}_i^C -N_i^*\right) /\left( \hat{N}_i^C N_j^*\right)\), where \(N_i^*\) and \(N_j^*\) are the equilibrium densities of species i and j in the two-species community. By this procedure, the growth rates of both species are correct when no species are present, i.e., \(f_i(0,0)\), at the two-species equilibrium, i.e., \(f_i(N_i^*, N_j^*)\) and at their own monoculture equilibrium, i.e., \(f_i(\hat{N}_i^C,0)\).
However, the ZNGI may not be linear, in which case such a linear representation of the ZNGI will necessarily be an approximation. Importantly, the invasion growth rate of species i, its growth rate when the resident species j is at its monoculture equilibrium density, i.e., \(f_i(0,\hat{N}^C_j)\), may not be correctly approximated, as we only fit the growth rate at its own monoculture equilibrium density. We show below, that the approximations do sometimes incorrectly approximate the equilibrium densities. Table 1 summarizes the linear representation for all these models. Given the interaction coefficients \(\alpha _{ij}\) we can compute \(\mathcal {N}^A\;\text {and}\;\mathcal {F}^A\) as (Chesson 2018):
Note that we slightly change the definition of \(\mathcal{F}^A_i\) by defining \(\mathcal {F}^A_i = 1-\sqrt{\frac{\alpha _{ii}\alpha _{ij}}{\alpha _{ji}\alpha _{jj}}}\) instead of the more usual \(\mathcal {F}^A_i= \sqrt{\frac{\alpha _{ii}\alpha _{ij}}{\alpha _{ji}\alpha _{jj}}}\). This change is purely aesthetic to ensure consistency between \(\mathcal {N}^A_i\) and \(\mathcal {F}^C_i\), it does not affect the properties of \(\mathcal {N}^A\). Specifically, this ensures that the approximate model and the full model, discussed below, have the same coexistence condition. Specifically, a species is assumed to coexist if \(\mathcal {F}^A_i<\frac{\mathcal {N}^A_i}{1-\mathcal {N}^A_i}\).
Niche and fitness differences based on the full model
We computed \(\mathcal {N}^C\;\text {and}\;\mathcal {F}^C\) for the full model based on a recently developed method (Spaak and De Laender 2020). Briefly, this method ensures that species with independent feedback loops have \(\mathcal {N}^C= 1\), while species with equivalent feedback loops have \(\mathcal {N}^C= 0\). Thus, the method critically depends on whether invasion analysis can predict coexistence for the model it is applied to (Spaak and De Laender 2020; Barabas et al. 2018; Chesson 1994; Pande et al. 2019). More precisely, for a model given by the per-capita growth rate \(\frac{1}{N_i}\frac{dN_i}{dt} = f_i(N_i,N_j)\) Spaak and De Laender (2020) define \(\mathcal {N}^C\;\text {and}\;\mathcal {F}^C\) as
where \(\hat{N}_j^C\) is, as above, the monoculture equilibrium density of species j. A conversion factor, \(c_j\), which converts densities of species j to densities of species i, ensures that both species have the same dependence on limiting factors, i.e., equally strong feedback loops. \(c_j\) is the solution of the equation \(|1-\mathcal {N}^C_i|=|1-\mathcal {N}^C_j|.\)
Equation 4 compares the actual invasion growth rate of species i (\(f_i(0,\hat{N}_j^C)\)) to the hypothetical invasion growth rate when the two species had independent feedback loops (\(f_i(0,0)\)) and to another hypothetical invasion growth rate when the two species had identical feedback loops (\(f_i(c_j\hat{N}_j^C, 0)\)). Two species coexist if the niche differences of both species are strong enough to overcome fitness differences, i.e., \(\mathcal {F}^C_i<\frac{\mathcal {N}^C_i}{1-\mathcal {N}^C_i}\).
Predicting and understanding coexistence
For \(\mathcal {N}^A\;\text {and}\;\mathcal {F}^A\) or, \(\mathcal {N}^C\;\text {and}\;\mathcal {F}^C\), to predict coexistence they need to correctly predict the outcome of species interactions. For a two-species community there are three such outcomes (Tilman 1982).
A first outcome is priority effects, where the outcome of competition depends on the starting conditions, this is only possible with positive frequency dependence, i.e., negative niche differences (Ke and Letten 2018). A second outcome is coexistence, where both species persist indefinitely, this is only possible with negative frequency dependence, i.e., positive niche differences. A third outcome is competitively exclusion, where the competitive dominant species excludes the other species. This is consistent with both negative or positive niche differences, and depends on the fitness differences (\(\frac{1-\mathcal {N}^C}{\mathcal {N}^C}\mathcal {F}^C<-1\)). When \(\mathcal {N}^C\;\text {and}\;\mathcal {F}^C\) or, \(\mathcal {N}^A\;\text {and}\;\mathcal {A}^A\) predict these three outcomes for a given model, we consider these to correctly predict coexistence.
For \(\mathcal {N}^A\;\text {and}\;\mathcal {F}^A\) or, \(\mathcal {N}^C\;\text {and}\;\mathcal {F}^C\) to be used to understand coexistence, they need to reflect the mechanisms driving the outcome of species interactions. \(\mathcal {N}\) measures the difference between the niches of two species. When the two species do not interact with each other, because they occupy completely different niches, then \(\mathcal {N}\) should reflect total niche differences, i.e., \(\mathcal {N}= 1\) (Spaak and De Laender 2020; Spaak et al. 2021). Conversely, if two species occupy the same niche, then \(\mathcal {N}\) should be 0. Testing whether two species occupy the same niche is difficult in general, as one may not know whether the species do differ in any niche axis not tested for. However, in the special cases where there is only one limiting factor, e.g., because species compete for only one resource or resources go extinct, species must occupy the same niche.
In addition, to understand species coexistence, \(\mathcal {N}^A\;\text {and}\;\mathcal {A}^A\) or, \(\mathcal {N}^C\;\text {and}\;\mathcal {F}^C\), need to categorize a change in a model’s parameter as a stabilizing and/or equalizing mechanism. That is, changes that increase niche differences are called stabilizing, while they are equalizing when they decrease fitness differences. For simplicity we will use the terms stabilizing and equalizing for both increases and decreases in niche differences or fitness differences, respectively. Importantly, mechanisms can be both stabilizing and equalizing. We will call any mechanism that only affects niche or fitness differences purely stabilizing or equalizing, respectively. We tested for all model parameters whether they are stabilizing or equalizing according to \(\mathcal {N}^A\;\text {and}\;\mathcal {F}^A\) or, \(\mathcal {N}^C\;\text {and}\;\mathcal {F}^C\).
Results
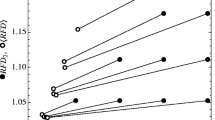
Implicitly, \(\mathcal {N}^A\;\text {and}\;\mathcal {F}^A\) are linear approximations of the per-capita growth rates, i.e., \(f_i(N_i,N_j)\approx r_i\cdot (1-\sum _j \alpha _{ij}N_j)\) (Fig. 1). Through this approximation we often lose information about community dynamics, most notably higher order interactions (Grilli et al. 2017; Levine et al. 2017), such as resource extinctions or explicit information about interactions with limiting resources (Letten and Stouffer 2019). Specifically, the linearization does not account for the possibility of substitutable resources going extinct (Chesson and Kuang 2008; Letten et al. 2017), or for the fact that the identity of the essential resource that is limiting to a species can change during competition, independent of changes in the resource supply rates (Letten et al. 2017). Importantly, the community model is approximated near the equilibrium of the system; however, it is evaluated away from the equilibrium at the invasion growth rates of the species. This difference between where the approximation is performed and where it is evaluated leads to a poor approximation of the growth rates, and of the invasion growth rate especially, for all four models (Fig. 1).
When species drive resources to extinction the approximation given in Table 1 may lead to an incorrect prediction of coexistence. That is two species may have \(\mathcal {F}^A>\frac{\mathcal {N}^A}{1-\mathcal {N}^A}\) but coexist nonetheless, or they may have \(\mathcal {F}^A<\frac{\mathcal {N}^A}{1-\mathcal {N}^A}\) but not coexist. However, in this case the approximation would also lead to different equilibrium densities, i.e., \(1-\sum _j\alpha _{ij}N_j^* \ne 0\), we therefore do not focus further on these cases. However, we caution that one must verify that the linear approximation indeed holds for the equilibrium condition (Appendices S1 and S2).
Accounting for complexity enhances understanding of coexistence
Both the approximation and the full niche and fitness differences predict the case where the two species do not interact and must have \(\mathcal {N}=1\) in all four community models. For the other cases, \(\mathcal {N}^C\;\text {and}\;\mathcal {F}^C\) improve our understanding of coexistence.
For certain resource supply rates both species will drive one resource to extinction in monoculture (Fig. 2 above blue dotted line or below green dotted line). In this case, the ZNGI of the species is non-linear and a linear representation will necessarily lose precision, irrespective of how exactly the linear representation of the model is chosen. When one resource is driven to extinction, both species effectively compete only for one resource and must have identical feedback loops and no niche differences. For all resource explicit models, \(\mathcal {N}^C\) can identify this case (i.e., \(\mathcal {N}^C= 0\)). However, \(\mathcal {N}^A\ne 0\) for these resource supply rates for the substitutional resource models (Fig. 2A, B). Additionally, under competition for essential resources, the linearization method predicts \(\mathcal {N}^A=0\) for a community with priority effects (Appendix S2), which contradicts prior findings (Ke and Letten 2018; Mordecai 2011; Spaak and De Laender 2020). Both the approximated \(\mathcal {N}^A\;\text {and}\;\mathcal {A}^A\) and the full \(\mathcal {N}^C\;\text {and}\;\mathcal {F}^C\) give exactly the same predictions for the absence of niche difference in the annual plant model, i.e., \(\mathcal {N}^C=0\Leftrightarrow \mathcal {N}^A=0\), which we interpret as both methods correctly predicting if the two species occupy the same niche.
Any mechanism that is purely equalizing cannot alter the outcome of competition from coexistence to priority effects or vice versa (Ke and Letten 2018). We found that changes in mortality or resource supply rates can alter the outcome of competition from priority effects to coexistence in certain conditions, and therefore must be stabilizing (Appendix S1). \(\mathcal {N}^C\;\text {and}\;\mathcal {F}^C\) identify these mechanisms, as they affect \(\mathcal {N}^C_i\) (Fig. 3). Conversely, the linear approximations classify any mechanism in the resource competition models that does not affect resource utilization \(u_{li}\) or the conversion efficiency \(w_{il}\) as purely equalizing; mechanisms that affect \(u_{li}\) or \(w_{il}\) are both equalizing and stabilizing (Table 2).
Alternatively, we can see that changes in resource supply rates can be stabilizing in the following scenario. Given two species, the resource supply rates determine whether both species are limited by the same resources (and consequently must have \(\mathcal {N}= 0\)) or whether the species coexist (and consequently must have \(\mathcal {N}>0\)). Therefore, changes in resource supply rates can be stabilizing mechanisms. In general, \(\mathcal {N}^C\;\text {and}\;\mathcal {F}^C\) predict that essentially all mechanisms are both stabilizing and equalizing (Song et al. 2019).
Importantly, the new interpretation that changes in mortality or resources supply rates are stabilizing is not based on the specificities of \(\mathcal {N}^C\;\text {and}\;\mathcal {F}^C\). Rather, we draw this argument based on intuitive knowledge of niche differences only. It should therefore apply to any reasonable definition of niche and fitness differences (Appendix S1).
The interpretation of stabilizing and equalizing mechanisms in the annual plant model depends on the method to assess niche and fitness differences. Using \(\mathcal {N}^A\;\text {and}\;\mathcal {A}^A\), we would interpret that only mechanisms affecting \(\alpha _{ij}\) can be stabilizing, all other mechanisms are purely equalizing. Conversely, using \(\mathcal {N}^C\;\text {and}\;\mathcal {F}^C\) we would interpret that essentially all mechanisms are both stabilizing and equalizing, including changes in intrinsic growth rates, seed survival and seed mortality rates (Fig. 3). However, we do not know which of these two interpretations is more useful, as the arguments used for the resource explicit models do not apply for the annual plant model.
Accounting for complexity reveals new phenomena
A first new insight is the existence of local maxima and minima for \(\mathcal {N}^C\). Importantly, the location of these local maxima and minima can be constructed geometrically, similar to how the coexistence region can be constructed (Appendix S3). The existence of these maxima and minima is unexpected, but not counter-intuitive. Imagine the scenario where we keep all community parameters fixed except \(S_1\), the supply rate of the first resource. For \(S_1\) much smaller than \(S_2\), both species are limited by \(R_1\) only, hence we must have zero niche differences, when \(S_1\) and \(S_2\) are comparable the species coexist, hence we expect positive niche differences, for much larger \(S_1\) than \(S_2\) the species are limited by \(R_2\), hence we expect again zero niche differences. Consequently, \(\mathcal {N}\) should depend in a non-monotonic way on \(S_1\) and will therefore exhibit a maximum. We should therefore expect that \(\mathcal {N}\) depends in a non-monotonic way on both \(S_l\), as it indeed does.
Another new insight from \(\mathcal {N}^C\;\text {and}\;\mathcal {F}^C\) is that competition for substitutable resources can lead to negative \(\mathcal {N}^C_i\), i.e., positive frequency dependence, for certain resource supply rates. However, even for these resource supply rates, the community will not exhibit priority effects. This highlights that negative niche differences (and thus positive frequency dependence) are necessary but not sufficient conditions for priority effects. If fitness differences are too strong, one species will exclude the other, regardless of the initial condition, which is the case in this scenario (Ke and Letten 2018).
Positive frequency dependence arises when species consume more of the resource that limits their competitor most (Ke and Letten 2018; Tilman 1982). For the resource supply rates chosen in Fig. 2D the blue species drives resource 2 to extinction in monoculture. The green species, as an invader, will therefore only consume resource 1 and have a horizontal utilization vector. The green species therefore consumes only the favored resource of its competitor (blue species), which leads to positive frequency dependence (Ke and Letten 2018). A condition for \(\mathcal {N}^C<0\) is therefore that resources go extinct, which is why \(\mathcal {N}^C<0\) does not occur for essential resources as species in monoculture cannot drive essential resources to extinction.
Discussion
An often used approach to compute niche and fitness differences is to represent the equilibrium dynamics of the community model with a linear model (Godwin et al. 2020; Godoy and Levine 2014; Letten et al. 2017; Chesson 2013; Johnson 2021). We have found that including non-linear species interactions improves our ability to understand coexistence, and yields three important new insights compared to linearization-based approaches.
First, changes in mortality rates can affect both niche and fitness differences, contrary to earlier results (Chesson 2000; Godoy et al. 2014; Barabas et al. 2018; Petry et al. 2018; Letten et al. 2017). This confirms the earlier findings from Song et al. (2019) who found that niche and fitness differences are interdependent. Except in some special cases, changing any parameter always affected both niche and fitness differences. We found no mechanism that acts solely as equalizing or stabilizing.
Second, niche differences depend non-monotonically on the resource supply rates and environmental conditions. Again, this result is independent of the specific properties of \(\mathcal {N}^C\;\text {and}\;\mathcal {F}^C\), but is based on intuitive properties of niche and fitness differences (see Appendix S1). We also found maxima and minima of niche differences as a function of resource supply. While we were able to show the existence and specific location of such extremes, we know little about their consequences. For example, niche differences are assumed to increase ecosystem function (Carroll et al. 2011; Striebel et al. 2009) or stability with respect to perturbation (Adler et al. 2007). The extent to which these supply rates translate to higher functioning and greater stability remains to be verified.
Third, niche differences based on non-linear community models highlight resource supply rates that result in negative \(\mathcal {N}^C\) (Fig. 2). At these resource supply rates, species have positive frequency dependence, which was unknown for this well-known community model. However, despite the positive frequency dependence and negative niche differences, the system is not driven by priority effects, as fitness differences are too strong (Ke and Letten 2018).
Niche and fitness differences should facilitate understanding of species coexistence by disentangling stabilizing from equalizing mechanisms. We have shown that essentially all mechanisms are both stabilizing and equalizing, as they can alter the outcome of competition from priority effects to coexistence. This is perhaps not surprising when the full non-linear dynamics are taken into account. Nevertheless, we would still anticipate that any given shift of traits or environment conditions will often be more strongly stabilizing or equalizing. It will be valuable in future work to identify the conditions under which equalizing and stabilizing mechanisms exhibit weaker or stronger interdependence. Decomposition methods that account for non-linear interactions will be critical to achieving this objective.
Future directions of niche and fitness differences
Recent research has shown that non-linear or higher order species interactions can affect community composition, community stability and coexistence (Grilli et al. 2017; Bairey et al. 2016; Mayfield and Stouffer 2017; Singh and Baruah 2019). We have shown that niche and fitness differences can be used to understand why non-linear and higher order species interactions, such as resource extinctions or changes in limiting resources, can affect community dynamics; however, our results remain limited to simple two-species communities. Applying niche and fitness differences, which include non-linear and higher order interactions, to more complex multi-species communities is an important next step to understand the effects of non-linear or higher order effects on population dynamics (Godoy et al. 2018; Letten and Stouffer 2019).
Modern coexistence theory and niche and fitness differences in particular should help us to predict and understand species coexistence. We have shown that two different methods to assess niche and fitness differences result in different interpretations of the underlying processes. However, there are a total of thirteen different methods to assess niche and fitness differences, with little consensus about which to use (Godwin et al. 2020; Spaak et al. 2022b). Some of these methods can account for non-linear species interactions, some of them cannot. Our results imply that these different methods can potentially lead to different interpretations of the underlying processes. For example, the methods of Carroll et al. (2011); Zhao et al. (2016) and Carmel et al. (2017) interpret essentially all processes as both equalizing and stabilizing, but to different extents (Appendix S4). Similarly, niche differences of Carroll et al. (2011) and Zhao et al. (2016) depend non-monotonically on resource supply rates, but niche differences of Carmel et al. (2017) do not. Additionally, Song and Saavedra (2020) have shown that a mechanism increasing structural niche differences (Saavedra et al. 2017) may decrease niche differences as measured by the linearization approach. In short, our interpretation of stabilizing mechanisms depends on the method to assess niche differences (Spaak et al. 2022b).
The method to compute \(\mathcal {N}^A\;\text {and}\;\mathcal {F}^A\) implicitly approximates the actual community model \(f_i(N_i,N_j)\) with a linear per-capita growth rate \(r_i(1-\alpha _{ii}N_i-\alpha _{ij}N_j)\). e show this approximation explicitly as the scaled per-capita growth rates of the focal species (y-axis) as a function of the resident species density (x-axis) for the four full models (solid line \(=f_i(0,N_j)/f_i(0,0)\)) and their linear approximations (dashed \(=1-a_{ij}N_j\)). The linear approximations do not capture the full complexity of the models and deviate substantially from the full model. Two main differences between the approximation and the full model stand out: First (A and B), the approximated equilibrium density of the resident \(\hat{N}_j^A\) is smaller than the exact resident’s equilibrium density \(\hat{N}_j^C\) (indicated by different labels for \(\hat{N}_j^A\) and \(\hat{N}_j^C\)). Second (A,B and C), the density for zero net growth is not equal for the approximation and the full model (intersection with gray line). These two differences occur because the linearization does not account for resources that go extinct (black triangles, A,B,C) or changes in which essential resource is limiting (black square, C). The full model eventually transforms into a horizontal line (A,B,C) when all resources are extinct and growth rates reduce to the density-independent mortality rates. However, species j would not naturally reach densities this high (i.e., above \(N_j^C\)). These differences can lead to wrong predictions about the outcome of competition (see Table 2). Chosen parameters (A,B,C) are equivalent to Fig. 2
\(\mathcal {N}\) (color) as a function of the resource supply rates for the three different resource explicit community models. \(\mathcal {N}^A\) and \(\mathcal {N}^C\) are not defined when one species cannot survive in monoculture (white regions). A,B: \(\mathcal {N}^A\) is independent of resource supply rates for substitutable resources. Moreover, the functional response to resource concentrations does not affect \(\mathcal {N}^A\) (given \(u_{li}\) and \(w_{il}\)). In the region where both species are limited by only one resource (above blue dotted and below green dotted line) \(\mathcal {N}^A\) is non-zero, contrary to the assumption that species competing for one resource must have \(\mathcal {N}=0\). C: \(\mathcal {N}^A\) is only affected by changes in the resource supply rates if the limiting resource changes for a species (crossing a dotted line). This change from \(\mathcal {N}^A\ne 0\) to \(\mathcal {N}^A=0\), however, is discontinuous. D,E,F: \(\mathcal {N}^C\) continuously depends on changes in resource supply rates and features local maxima (D-F) and minima (D,E). \(\mathcal {N}^C\) identifies cases where \(\mathcal {N}^C=0\) in the region where both species are limited by the same resource. Green and blue solid lines are the ZNGI, dashed lines delimit the coexistence region and dotted lines delimit the region where both species are limited by the same resource. Black dot represents the resource supply rates taken for Figs. 1 and 3
\(\mathcal {N}^C\) (color) as a function of mortality for the four investigated models. Mortality has a non-monotonic effect on \(\mathcal {N}^C\) and may lead to local maxima and minima of \(\mathcal {N}^C\) (panel B), similar to changes in the resource supply rates. Blank areas (Panel B) indicate too high mortality for species persistence. Parameters (except mortality) are chosen such as in Fig. 2, the black dot represents the same mortality as in Fig. 2
Data availability
The study used no empirical data.
Data accessibility
All computer code used in this manuscript will be made publicly available on figshare.
Code availability
All code used in the project will be made publicly available. The code is all written in Python, a publicly available open-access programming language.
References
Adler PB, HilleRislambers J, Levine JM (2007) A niche for neutrality. Ecol Lett 10:95–104
Bairey E, Kelsic ED, Kishony R (2016) High-order species interactions shape ecosystem diversity. Nat Commun 7:1–7
Barabas G, D’Andrea R, Stump SM (2018) Chesson’s coexistence theory. Ecol Monogr 88:277–303
Buche L, Spaak JW, Jarillo J, De Laender F (2022) Niche differences, not fitness differences, explain predicted coexistence across ecological groups. J Ecol 110:2785–2796
Carmel Y, Cornell SJ, Belmaker J, Suprunenko YF, Kent R, Kunin WE, Bar-Massada A (2017) Using exclusion rate to unify niche and neutral perspectives on coexistence. Oikos 126:1451–1458
Carroll IT, Cardinale BJ, Nisbet RM (2011) Niche and fitness differences relate the maintenance of diversity to ecosystem function. Ecology 92:1157–1165
Chesson P (1990) MacArthur’s consumer-resource model. Theor Popul Biol 37:26–38
Chesson P (1994) Multispecies Competition in Variable Environments. Theor Popul Biol 45:227–276
Chesson P (2000) Mechanisms of maintenance of species diversity. Evol Syst Annu Rev Ecol p. 31
Chesson P (2013) Species Competition and Predation. Ecological Systems. Springer, New York, pp 223–256
Chesson P (2018) Updates on mechanisms of maintenance of species diversity. J Ecol 106:1773–1794
Chesson P, Kuang JJ (2008) The interaction between predation and competition. Nature 456:235–238
Godoy O, Bartomeus I, Rohr RP, Saavedra S (2018) Towards the Integration of Niche and Network Theories
Godoy O, Levine JM (2014) Phenology effects on invasion success: Insights from coupling field experiments to coexistence theory. Ecology 95:726–736
Godoy O, Kraft NJ, Levine JM (2014) Phylogenetic relatedness and the determinants of competitive outcomes. Ecol Lett 17:836–844
Godwin CM, Chang FH, Cardinale BJ (2020) An empiricist’s guide to modern coexistence theory for competitive communities. Oikos
Grilli J, Barabas G, Michalska-Smith MJ, Allesina S (2017) Higher-order interactions stabilize dynamics in competitive network models. Nature 548:210–213
Holt R, Grover J, Tilman D (1994) Simple Rules for interspecific dominance in systems with exploitative and apparent competition. Am Nat 144:741–771
Johnson CA (2021) How mutualisms influence the coexistence of competing species. Ecology
Ke PJ, Letten AD (2018) Coexistence theory and the frequency-dependence of priority effects. Nature Ecology and Evolution 2:1691–1695
Letten AD, Stouffer DB (2019) The mechanistic basis for higher-order interactions and non-additivity in competitive communities. Ecol Lett 22:423–436
Letten AD, Ke PJ, Fukami T (2017) Linking modern coexistence theory and contemporary niche theory. Ecol Monogr 87:161–177
Levine JM, Bascompte J, Adler PB, Allesina S (2017) Beyond pairwise mechanisms of species coexistence in complex communities. Nature 546:56–64
Mayfield MM, Stouffer DB (2017) Higher-order interactions capture unexplained complexity in diverse communities. Nature Ecology and Evolution 1:1–7
Meszena G, Gyllenberg M, Pasztor L, Metz JA (2006) Competitive exclusion and limiting similarity: A unified theory. Theor Popul Biol 69:68–87
Mordecai EA (2011) Pathogen impacts on plant communities: unifying theory, concepts, and empirical work. Ecol Monogr 81:429–441
Pande J, Fung T, Chisholm R, Shnerb NM (2019) Mean growth rate when rare is not a reliable metric for persistence of species. Ecol Lett 23:274–282
Petry WK, Kandlikar GS, Kraft NJ, Godoy O, Levine JM (2018) A competition-defence trade-off both promotes and weakens coexistence in an annual plant community. J Ecol 106:1806–1818
Saavedra S, Rohr RP, Bascompte J, Godoy O, Kraft NJ, Levine JM (2017) A structural approach for understanding multispecies coexistence. Ecol Monogr 87:470–486
Singh P, Baruah G (2019). Higher order interactions and coexistence theory. Theo Ecol
Song C, Barabas G, Saavedra S (2019) On the consequences of the interdependence of stabilizing and equalizing mechanisms. The American Naturalist pp. 000-000
Song C, Saavedra S (2020) Telling ecological networks apart by their structure: An environment-dependent approach. PLoS Comput Biol 16
Spaak JW, Adler PB, Ellner SP (2022a) Modeling phytoplankton-zooplankton interactions: opportunities for species richness and challenges for modern coexistence theory. bioRxiv
Spaak JW, De Laender F (2020) Intuitive and broadly applicable definitions of niche and fitness differences. Ecol Lett https://doi.org/10.1101/482703
Spaak JW, Carpentier C, De Laender F (2021) Species richness increases fitness differences, but does not affect niche differences. Ecol Lett 24:2611–2623
Spaak JW, Godoy O, De Laender F (2021) Mapping species niche and fitness differences for communities with multiple interaction types. Oikos 130:2065–2077
Spaak JW, Ke PJ, Letten AD, DeLaender F (2022b) Different measures of niche and fitness differences tell different tales. Oikos p. e09573
Striebel M, Behl S, Diehl S, Stibor H (2009) Spectral Niche Complementarity and Carbon Dynamics in Pelagic Ecosystems. Am Nat 174:141–147
Tilman GD (1982) Resource Competition and Community Structure. Princeton University Press
Zhao L, Zhang QG, Zhang DY (2016) Evolution alters ecological mechanisms of coexistence in experimental microcosms. Funct Ecol 30:1440–1446
Funding
Open Access funding enabled and organized by Projekt DEAL. F.D.L. received support from grants of the University of Namur (FSR Impulsionnel 48454E1) and the Fund for Scientific Research, FNRS (PDR T.0048.16).
Author information
Authors and Affiliations
Contributions
All authors conceived the study. J.W.S. and R.M. wrote the computer code. J.W.S. created the figure and performed the analysis. J.W.S. wrote the first draft. All authors discussed content and contributed to revisions.
Corresponding author
Ethics declarations
Ethics approval
Not applicable
Consent to participate
Not applicable
Consent for publication
All authors agreed to be listed as authors.
Conflict of interest
The authors declare no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Spaak, J.W., Millet, R., Ke, PJ. et al. The effect of non-linear competitive interactions on quantifying niche and fitness differences. Theor Ecol 16, 161–170 (2023). https://doi.org/10.1007/s12080-023-00560-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12080-023-00560-6