Abstract
Bet-hedging strategies help organisms to decrease variance in their fitness in unpredictably changing environments, by which way lineage fitness can be maximized in the given environment. As one strategy, diversified bet-hedging helps to achieve that by increasing phenotypic variation in fitness-related traits. For example, in diversified tracking, parents may divide the developmental phenotypes of their offspring within broods, leading to cohort splitting among the progeny. Such diversification, though, should be probabilistic and sensitive to no external stimuli. However, it was recently highlighted that plasticity in response to environmental stimuli may be part of a more dynamic case of bet-hedging. Current understanding and empirical observations of such a plastic bet-hedging remain limited. Here I use a theoretical investigation relying on empirical grounds in a specific case of cohort splitting in the wolf spider Pardosa agrestis (Westring 1861). I investigated whether cohort splitting might be a bet-hedging strategy in females of P. agrestis, and whether it would be expected to be static or plastic bet-hedging. Results show that cohort splitting is likely a bet-hedging strategy in this species, by which females maximize their lineage fitness. Also, cohort splitting appears to arise from plastic bet-hedging, as in simulated populations where both static and plastic bet-hedging females occur, the latter have considerably higher geometric mean fitness. I discuss theoretical and empirical observations in light of the current theory, and draw predictions on specific aspects of this case of plastic bet-hedging.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Developmental plasticity and cohort splitting
While the progress in ontogeny is firmly regulated by highly conserved genes, substantial variation can exist in some developmental characteristics within species or even populations in the form of phenotypic plasticity (West-Eberhard 2003). Such developmental plasticity is often evoked by more or less dynamic environmental characteristics, shaping organisms’ phenotypes to increase their chances of survival in variable environments. Adaptive developmental plasticity may not only buffer a given genotype’s capacity to fare well under a range of environmental conditions but may also contribute to the emergence of different developmental pathways in the population. An interesting scenario is when this plasticity results in a phenomenon called cohort splitting, in which individuals of the same age group (i.e. cohort) follow different routes of development, leading to the simultaneous presence of multiple developmental pathways in the population (Crowley and Hopper 2015). Cohort splitting is hypothesized to be a consequence of adaptive developmental plasticity in response to temporal or spatial variations in habitat quality, and was suggested to contribute to the evolution of optimal life history strategies in environments where environmental states show stochastic changes of considerable magnitude (Benton and Grant 1999; Tuljapurkar 1990).
Intriguingly, one of the ultimate mechanisms that might orchestrate cohort splitting, called diversified tracking, can result from diversified bet-hedging (Crowley and Hopper 2015). As bet-hedging in general, diversified tracking is hypothesized to help individuals to maximize long-term fitness in unpredictably changing environments, by reducing variance in the expected reproductive successes (Starrfelt and Kokko 2012). In diversified tracking, parents may spread the risk of total reproductive failure over multiple offspring phenotypes by probabilistically assigning the offspring to alternative developmental types, hence increasing the likelihood that at least some of them will survive until maturation and successful reproduction (Crowley et al. 2016; Einum and Fleming 2004).
Classically, bet-hedging is considered to be a purely probabilistic strategy, exactly because the state of the environment in which the offspring will develop cannot be predicted. However, recently it was highlighted that more dynamic bet-hedging strategies can arise when some level of environmental variability can be utilized to incur adaptive phenotypic responses, but still within the framework of bet-hedging (Frankenhuis et al. 2016; Grantham et al. 2016; Sadeh et al. 2009). That is, environmental cue-specific plasticity can evolve as a form of bet-hedging, in which different levels of offspring plasticity are optimal in different environmental states. In such a scenario, the future state of the environment is still not predictable, but varying offspring plasticity could contribute to the appearance of alternative phenotypes that diverge in response to certain environmental conditions.
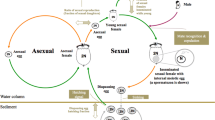
Studying this “plastic bet-hedging” is still difficult, in part due to our limited knowledge on organisms in which it may have evolved. One promising invertebrate species, with a unique case of cohort splitting that might be of great relevance and importance to such studies, is the wolf spider Pardosa agrestis (Westring 1861), in which cohort splitting occurs among the early summer progeny, resulting from developmental asynchrony (Kiss 2003; Kiss and Samu 2002, 2005; Rádai et al. 2017). While some spiderlings develop throughout the year and will mature and reproduce (then perish) during the next early summer, others (even from the same broods) will exhibit much more rapid development, mature, reproduce, and perish during late summer or autumn of the same year they hatched in. Notably, P. agrestis mainly resides in arable habitats, alkaline grasslands, and marshes (Samu and Szinetár 2002), which are characterized by substantial year-to-year variation and unpredictable changes in quality. In the past it was hypothesized that its unique phenology might have helped P. agrestis to become dominant in these habitat types (Kiss and Samu 2005; Rádai et al. 2017). When considering the slowly and rapidly developing offspring of early summer females as alternative developmental phenotypes, the question might arise: Could it be beneficial for the females to split their brood into two sub-cohorts? As it was proposed by Rádai et al. (2017), differential survival (and/or reproductive success) of slowly and rapidly developing spiders in different environmental conditions might have contributed to the emergence of cohort splitting in this species. Indeed, when environmental quality varies unpredictably across the different years, and the alternative developmental types are most successful under specific sets of conditions, early summer females might be able to decrease the variance in their fitness by diversifying their offspring’s phenotypes. If so, we would expect to see that (1) there is low variance between mothers in the developmental characteristics of offspring, while (2) within-mother variance would be relatively high. Also, (3) females (or, more specifically, genotypes) producing a mixed brood would be expected to have the highest lineage fitness, and (4) the optimal ratio of developmental types within a brood should strongly depend on the temporal dynamics of environmental states.
In such a scenario, though, we would expect to see that developmental characteristics of the spiderlings (and the proportion of rapidly developing individuals within broods) are independent of environmental factors; as in a diversified bet-hedging strategy, offspring should be designated to the alternative phenotypes probabilistically. Contrastingly, both indirect and direct observations indicate that environmental conditions experienced by the spiderlings of P. agrestis strongly and consistently affect the occurrence of the rapidly developing phenotype (Kiss 2003; Rádai et al. 2017, 2020). Concretely, higher ambient temperatures and long (or increasing) day length were found to increase developmental rate and the likelihood to mature without overwintering. These observations are not quite consistent with a static bet-hedging (Scheiner 2014; Simons 2011), while they may be consistent with plastic bet-hedging (Frankenhuis et al. 2016). Indeed, in an environment showing substantial temporal variation, selection was predicted to favour the evolution of plasticity within the brood, or even within-brood variation in the extent of plasticity itself (Frankenhuis et al. 2016).
Life history characteristics of P. agrestis
As described beforehand, cohort splitting occurs even within broods, i.e. early summer females most often have both slowly and rapidly developing offspring. Notably, increased developmental rate and cohort splitting can be induced in the laboratory among the offspring of both early and late summer adults, by applying increasing day length treatment that mimics early summer conditions (Rádai et al. 2020). Decreasing day length treatment, however, appears to decrease the spiderlings’ developmental rate, and to inhibit maturation. Also, even under quite favourable conditions (high, stable temperature and humidity, increasing day length, ad libitum food availability), not all spiderlings take on rapid development. On the other hand, when ambient temperature and food availability are high, a very small portion of the spiderlings might mature even in decreasing day length (mimicking late summer/autumn), but no spiders were observed to mature in low temperatures and short (or decreasing) day lengths (Kiss 2003; Rádai et al. 2020).
In Rádai et al. (2020), the applied light-cycle regime treatment consisted of rapid and slow developmental treatment groups (increasing and decreasing day lengths, respectively) to evoke developmental rate differences and cohort splitting among specimens. When analysing the developmental time of spiderlings (number of days from hatching to maturation) using mixed-effects linear regression modelling, with mother female as random grouping variable, it was found that the ratio of between-female variance to within-female variance in spiderlings’ developmental times is quite low (0.192; see Supplementary material), which is consistent with bet-hedging: Variation in the assessed trait is higher within than between mothers. Interestingly, however, between-female variation in responsiveness to treatment (assessed as random slope variance between females) was quite high (Supplementary material), which can be interpreted as substantial between-female variation in the propensity of offspring to take on rapid development in response to day length dynamics. Additionally, among females from which spiderlings originated, there was no correlation between the proportion of rapidly developing spiderlings reared in the rapid and the slow treatment groups, implying no strong genetic or maternal effects to play the role in determining the proportions of offspring developmental phenotypes. In other words, in females characterized by higher-than-average proportion of offspring that engaged in rapid development under rapid treatment (i.e. favourable conditions), the proportion of rapidly developing offspring under slow treatment (i.e. unfavourable conditions) was not higher-than-average (see Supplementary Fig. S1). Taken together, these observations seem to suggest that not only is cohort splitting dependent on environmental factors but that spiderlings’ propensity (i.e. their plasticity) to engage in rapid development is female (or lineage) dependent, rather than is the average proportion of rapidly developing offspring within broods.
Also in Rádai et al. (2020), it was found that in the laboratory, rapidly developing spiders do not show higher juvenile mortality than slowly developing ones; in fact, spiderlings in the rapid developmental treatment were less likely to perish as juveniles than were their siblings in the slow treatment group. It is worth noting though that laboratory rearing conditions are likely quite favourable, i.e. might represent a “good” environmental state. However, in Rádai et al. (2017) it was suggested that adverse environmental conditions might affect mortality differently for the developmental types, presumably having a more devastating impact on the survival of rapidly developing spiderlings. Although there is no explicit information on the juvenile (or overall) mortality of slowly and rapidly developing spiders reared in adverse conditions yet, environmental state-dependent differential survival (and reproductive success) of the developmental types would be consistent with a bet-hedging scenario. Indeed, if slowly developing spiders are relatively more successful in a specific environmental state (e.g. bad/adverse) than rapidly developing ones, while the opposite is the case in the other (good/favourable) environmental state, females from which the spiderlings originated can decrease variance in their fitness by producing both developmental phenotypes. Producing such a mixed brood might substantially decrease the probability of total reproductive failure in an environment where environmental states alternate unpredictably between the different years.
Aims
Building on the works of Crowley et al. (2016), Frankenhuis et al. (2016), and Starrfelt and Kokko (2012), I aimed to assess whether cohort splitting in P. agrestis could be a bet-hedging strategy on the part of early summer females, using a theoretical investigation, while relying on empirical data and observations on the life cycle and life history traits of this species. I also wanted to assess whether a classical (static) or a more dynamic (plastic) case of bet-hedging provides the highest fitness pay-off in a population where both occur. Based on theory, a static bet-hedging strategy could be expected when spiderlings of the diverging sub-cohorts gain fitness advantage from their respective developmental pathways. Also, in a static bet-hedging scenario, one would observe that diversifying offspring developmental phenotype of both early and late summer females decreases variation in their effective reproductive success, and/or increases arithmetic mean fitness without increasing variation in offspring viability. An example is when cohort splitting promotes niche partitioning and the consequent decrease in intra-specific competition. However, when cohort splitting during late summer would increase variance in effective reproductive success of parents, natural selection would be expected to suppress the developmental divergence of late summer spiderlings, leading to higher geometric mean fitness in lineages where no late summer cohort splitting occurs.
Methods
Reproductive success in a variable environment
For the present theoretical investigation, fecundity of developmental types was estimated using empirical data from cocoon carrying females, collected in natural habitats. Collection of cocoon carrying females was done in 2015, 2016, and 2017, at an uncultivated plot between Hajdúszoboszló and Nádudvar, Hungary. In 2015, 8 late summer (i.e. rapidly developing) females were collected. In 2016, we collected 28 and 13 cocoon carrying females during early and late summer (i.e. slowly and rapidly developing females), respectively, and in 2017, we collected 25 and 55 females during early and late summer, respectively. Females were reared in laboratory (with food and water provided ad libitum) until their spiderlings hatched, after which hatchlings were counted. Intriguingly, there is quite a marked difference between slowly and rapidly developing females in terms of their fecundity (Rádai et al. 2019, 2020). On average, slowly developing females (collected in early summer) had 44 ± 14 offspring (mean ± standard deviation), while rapidly developing females (collected in late summer) had 22 ± 9.
Throughout this theoretical investigation, I aimed to model expected reproductive success of females, utilizing either a “static” (i.e. when the ratio of alternative developmental types within females is not affected by environmental factors) or in a “plastic” bet-hedging strategy. In the latter, I consider offspring (among which cohort splitting might occur) to be so-called generalists, i.e. individuals that are capable of plastically responding to given environmental stimuli, and hence can exhibit different phenotypes in different environmental conditions (Frankenhuis et al. 2016). I hypothesize that these generalists are characterized by a heritable susceptibility to reliable environmental stimuli (such as day length) which determines their propensity to take on rapid development when conditions are favourable. I exclude modelling specialists among the offspring; specialists are low-plasticity individuals that are adapted to a given environmental state, having higher fitness pay-off than generalists when they encounter the “matching” environmental state, but pay a high fitness cost in the “mismatched” one (Frankenhuis et al. 2016). One might argue that rapidly developing spiders could be regarded as so-called safe-specialists (e.g. being relatively more successful in good conditions), whereas slowly developing spiders are danger-specialists (being relatively more successful in bad years). While rearing experiments suggest that rapidly developing spiders might indeed be more successful under favourable conditions (at least in terms of juvenile survival), note that specialists represent a low-plasticity strategy, ergo they would be expected to be present in broods in fixed proportions within females, irrespective of environmental factors. As described previously, however, the empirical observations show that the contrary is the case.
In the theoretical investigation I modelled the expected reproductive success of females (denoted as F0) reproducing at early summer (t0), defining reproductive success as the number of reproducing female descendants at the next early summer (t2). Spiders reside in an environment characterized by a stochastic year-to-year variation in environmental state (good versus bad), and neither mothers nor their offspring are able to predict the future state of the environment. In each year there is a fixed probability of the environmental state being “good”, and previous environmental states do not affect consecutive states (i.e. there is no temporal autocorrelation across years).
As a basis, I used a simplified form of the characteristic equation for reproduction rate (Roff 2002) to model expected reproductive success, modified to conform to a semelparous organism (i.e. number of reproductions is one, as is the case in P. agrestis (Rádai et al. 2019, 2018)):
where E denotes expected reproductive success of an early summer adult female at t2, m is mortality rate among her offspring (between hatching and reproduction), and f is the female’s fecundity, specified here as the number of female offspring produced. Extending this approach to include varying environmental states and the alternative developmental types within broods, we can calculate E in a static bet-hedging scenario as:
where s denotes environmental state (good or bad), and p(s) is the probability of environmental state s in any given year. Mortality of offspring (m) is a function of environmental state (s) and developmental type (λ) (slow or rapid), and d(λ) is the proportion of developmental type λ within the brood, which is fixed within mothers (that is to say, each female has a genotype coding for a specific value of d(rapid), i.e. for a specific proportion of rapidly developing offspring within the brood). Of course, for the developmental type proportions, it is true that d(rapid) = 1 – d(slow), and vice versa.
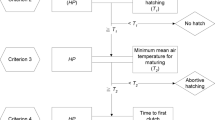
In a static bet-hedging scenario, we expect to see that the proportion of rapidly developing spiderlings within the brood of a female, and indeed, within the lineage of the given genotype, is fixed, meaning that d(rapid) has the same value in the early summer brood (hatching at t0) as in the late summer brood (hatching at t1, originating from the reproducing rapidly developing spiders that hatched at t0). As such, we would see two cohorts splitting within a year as follows: one taking place at early summer and one at late summer (Fig. 1). For this static bet-hedging scenario, we can calculate the expected number of reproducing female descendants of F0 at t2, given that the year bounded by t0 and t2 is in state s, as
Schematic representation of the hypothesized life cycle scenarios of P. agrestis: Early summer adult females (F0) produce offspring at early summer (t0), among which cohort splitting takes place. Within each female the proportions of slowly and rapidly developing spiderlings are given as d(slow, t0) and d(rapid, t0), respectively. While for each female these values are fixed, both in natural and laboratory reared populations (as well as in the simulated population in this study) there is considerable among-female variation in them. In a plastic bet-hedging scenario (right panel), while some of the spiderlings develop throughout the year, overwinter, then mature next early summer (t2), others take on rapid development, and mature and reproduce late summer the same year they hatched in (t1). Their offspring develop alongside the slowly developing spiderlings, and will mature next year (t2). In a static bet-hedging scenario (left panel), one would see cohort splitting among the late summer progeny (at t1) as well, i.e. two cohort splitting events would occur within a given year. Mortality patterns (representing the probability of a spiderling perishing before maturation and reproduction) that are specific to developmental types and time of year within the phenology are denoted as m(λ, t), in which λ represents developmental type (slow or rapid), and t represents time of year (t0 or t1)
where f0 is the number of female offspring originating from F0, and fR is the number of female offspring originating from a rapidly developing female. Mortality is now described as a function of environmental state (s), developmental type(λ), and time of year (t, which can take values t0 and t1 for early and late summer, respectively). The first part of the equation represents slowly developing spiderlings that hatched at t0 and mature at t2. The first half of the second part (within the first pair of square brackets) represents rapidly developing spiderlings that mature at t1. All of these rapidly developing spiders produce a brood each, within which cohort splitting also occurs due to the fixed, lineage-specific value of d(rapid). The number of offspring of such a brood is represented in the second pair of square brackets of the equation’s second part.
For the plastic bet-hedging scenario, we slightly modify d to be a function of developmental strategy and time of year, as d(λ, t), where t can be early or late summer (t0 or t1, respectively). Same as previously, d(rapid) represents average propensity of offspring to engage in rapid development (i.e. the probability that a given offspring will develop rapidly if adequate environmental stimuli occur). The value of d(rapid, t0) can range between zero and one during early summer across (but not within!) F0 females, whereas d(rapid, t1) value at late summer is zero, meaning that no rapidly developing spiderlings will be present among the offspring of late summer (t1) spiders. When d(rapid, t1) = 0, the previous equation attains a simpler form:
Note that the proportions of developmental types remain cumulative, i.e. when d(rapid, t1) = 0 then d(slow, t1) = 1 – d(rapid, t1) = 1. Based on these models of expected reproductive success, I carried out simulations, in order to assess (1) whether either type of bet-hedging (static or plastic) could be advantageous for F0 females, and if so, then (2) in a population where F0 females may utilize either static or plastic bet-hedging, which strategy proves to be more successful.
Based on current knowledge on the life cycle and life history characteristics of P. agrestis (see Introduction), I established four basic assumptions, namely:
-
i.
Overall mortality (from hatching to successful reproduction) should be lower in rapidly developing spiders than in slowly developing ones, if the current state of environment (i.e. given year) is good: m(good, rapid) < m(good, slow).
-
ii.
Overall mortality should be higher in rapidly developing spiders than in slowly developing ones, if the current state of environment is bad: m(bad, rapid) > m(bad, slow).
-
iii.
Mortality in good environmental state is not greater than in bad environmental state, in either slowly or rapidly developing spiders: m(bad) ≥ m(good).
-
iv.
Offspring of rapidly developing spiders (hatching at t1) do not have time to mature within the given year, therefore they mature at t2, at the same time as slowly developing spiders from t0 and t1.
Spiders of the different sub-cohorts likely differ in their overall mortalities, i.e. in the probability of perishing prior to reproduction. Slowly developing spiders hatching at t0 develop throughout the given year, and also have to survive overwintering to be able to mature at t2. Rapidly developing ones (also from t0) will not face overwintering, and will perish shortly after t1. Their offspring (developing from t1 to t2), however, will have to overwinter and mature in the next early summer (t2). Based on the life cycle of P. agrestis (see Fig. 1), mortality variables were specified for:
-
Slowly developing spiders, in good years: m(good, slow, t0)
-
Slowly developing spiders, in bad years: m(bad, slow, t0)
-
Rapidly developing spiders, in good years: m(good, rapid, t0)
-
Rapidly developing spiders, in bad years: m(bad, rapid, t0)
-
Slowly developing offspring of rapidly developing t0 spiders, in good years: m(good, slow, t1)
-
Slowly developing offspring of rapidly developing t0 spiders, in bad years: m(bad, slow, t1)
-
Rapidly developing offspring of rapidly developing t0 spiders, in good years: m(good, rapid, t1)
-
Rapidly developing offspring of rapidly developing t0 spiders, in bad years: m(bad, rapid, t1)
which variables determine the overall mortality pattern among the descendants of F0. For simplicity, m(s, λ, t0) values were used to calculate m(s, λ, t1) values as:
-
m(good, slow, t1) = m(good, slow, t0)
-
m(bad, slow, t1) = m(bad, slow, t0)
-
m(good, rapid, t1) = m(good, rapid, t0) + m(w) – m(good, rapid, t0) × m(w)
-
m(bad, rapid, t1) = m(bad, rapid, t0) + m(w) – m(bad, rapid, t0) × m(w)
where m(w) is overwintering mortality (set to 0.8, as overwintering is known to pose high mortality on epigeic wolf spiders: Kiss 2003; Kiss and Samu 2002; Schaefer 1977). Overwintering mortality did not vary either with environmental states or with developmental types, as developmental type differences in it are not expected, on the basis that developmental stage itself (i.e. number of moults, and being juvenile or subadult) does not appear to affect winter survival (Kiss 2003).
Simulations of geometric mean fitness
All pre-simulation parameter search, simulations, and data handling were done using the Julia programming language (ver. 1.1.1, Bezanson et al. 2017). To simulate geometric mean fitness in a simple in silico population of F0 females, firstly mortality patterns had to be identified, which conformed to the previously described criteria. A given mortality pattern can be thought of as a parameter set, including the eight mortality variables (with one specific value for each in a given set). Criteria-matching patterns were searched for heuristically, by searching the parameter space of the four “main” mortality variables (m(s, λ, t0), see previous sub-section). All possible combinations of values were tried with a precision of 0.01, from 0 to 1, i.e. each variable could have 101 potential values. As values were searched for four variables, a composite for-loop searched the “mortality parameter space” for 1014 possible value combinations. Using the mortality criteria, 4,082,925 patterns were found, but such a large number of mortality patterns would have been quite impractical and computationally extremely demanding to utilize. Therefore, 1000 mortality patterns were drawn randomly, on which later simulations relied.
In the simulations a population of F0 females was generated (N = 1000), each female representing a unique genotype coding for a unique value for the proportion of rapidly developing offspring within their broods (d(rapid)), ranging from zero to one within the population. Simulations ran for 1000 simulated years: In each year, the given environmental state (good or bad) was determined by drawing a single sample from a Bernoulli trial, where the probability of “success” was the probability of a year being “good” (p(good)). After it was established whether in the given year the environment was in a good or bad state, reproductive success (number of reproducing descendants at t2) was calculated for each female, on the basis of the previously described models. In all cases, the number of reproducing offspring was determined using Bernoulli trials: For a given female, the number of observations was set to one, while the number of trials was equal to the given female’s fecundity, and the probability of “success” (i.e. that a given offspring within the brood survives until reproduction) was one minus mortality rate (in accordance with the offspring’s developmental type, with the environmental state of the given year, and with the time of year).
This scheme was applied in three different scenarios of simulations, namely: (A) where all females had static bet-hedging (i.e. cohort splitting occurred both at t0 and t1), (B) where all females had plastic bet-hedging (i.e. cohort splitting occurred only at t0), and (C) where both static and plastic bet-hedging females (genotypes) were present in the population. In the latter, F0 females were randomly assigned to either static or plastic bet-hedging strategy (with 50% probability to being assigned to either), and did not change their strategy throughout the simulation. To quantify effective reproductive success of female genotypes over the 1000 simulated years, geometric mean fitness (GMF) was calculated, separately for each female:
where Y = 1000 (number of simulated years, each from t0 to t2), and Ey is number of reproducing descendants of the given F0 female at t2, in year y. When calculating geometric mean fitness, E had to be incremented by 1, because in some years it may have happened that a given genotype did not have reproducing descendants at all (Ey = 0), resulting in GMF = 0, even if in all other years Ey > 0.
Additionally, all simulations (including the three scenarios) were carried out three times, with the difference between simulation runs being that probability of good environmental state (p(good)) was set either to 0.25, 0.5, or 0.75. This way it was possible to see whether the optimal d(rapid) value depended on the temporal dynamics of the unpredictably changing environment.
Analyses of simulations
Data was mainly analysed using Julia, but for some analyses and for data visualization, I used the R statistical software (ver. 3.6.1, R Core Team 2018). From each of the simulations, I’ve acquired 3000 data tables (1000 for each simulation scenarios, i.e. for static, plastic, and mixed bet-hedging populations), each containing d(rapid) and GMF values for 1000 simulated F0 females. I was interested in those simulations in which the proportion of rapidly developing spiderlings (d(rapid)) associated with the highest geometric mean fitness was between 0 and 1, as would be expected in natural populations. This expectation is held toward all three scenarios: Both among static and plastic bet-hedging females, the value of d(rapid) linked to the most successful genotype should not either be zero or one, regardless of whether or not bet-hedging strategies are mixed or in monopoly in the population. Obviously, in the plastic bet-hedging strategy this goes only for d(rapid, t0) value (at early summer): The whole point of this plastic strategy is to have d(rapid, t1) = 0 (at late summer). In those simulations that met this criterion, I used linear regressions to model the association between d(rapid) and GMF in a given simulation (i.e. with a given mortality pattern). In these regressions, GMF was the dependent variable, while d(rapid) and its quadratic term d(rapid)2 were independent variables. Additionally, in the third scenario in which both static and plastic bet-hedging were present in the simulated population, female strategy (static or plastic) and its interactions with d(rapid) and d(rapid)2 were also included.
Results
Out of the total 3000 simulations from each specific p(good) value runs, the number of mortality patterns that resulted in 0 < d(rapid) < 1 in the populations, the static bet-hedging scenarios yielded the largest numbers of simulations meeting this criterion for d(rapid) (see Table 1), regardless of the value of p(good). The number of simulations were comparable within p(good) values when only plastic bet-hedging, or both static and plastic bet-hedging were present in the simulated population. Curiously, higher p(good) was associated with smaller number of simulations conforming to the 0 < d(rapid) < 1 criterion, in which only plastic bet-hedging or both static and plastic bet-hedging occurred.
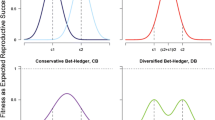
Overall it is clear that mortality patterns (conforming to the four assumptions described in the “Methods” section) exist in which the highest lineage fitness comes from broods of mixed developmental type offspring (Fig. 2a–i). Intriguingly, both static and plastic bet-hedging seem to be adaptive, in the sense that F0 females (genotypes) not producing either of the alternative developmental types in their brood were characterized by the lowest GMF. Even more importantly, in simulated populations where both static and plastic bet-hedging strategy females were present, F0 females with plastic bet-hedging strategy had consistently higher fitness than F0 females with static bet-hedging (Fig. 2j–l). Also noteworthy is the finding that events of reproductive failure (i.e. when a F0 female of a given genotype did not have any reproducing offspring in a given year) were less frequent among females of plastic bet-hedging: Averaged within simulations of different mortality patterns (over 1000 simulated years in each), out of the 1000 simulations in 46 was such reproductive failure observed in static bet-hedging females, whereas only 31 occurred in plastic bet-hedging females (Student’s paired t test on the log-transformed values: t = 41.46, P < 0.001).
Visualization of simulation results. Panels a–i show the association between the proportion of rapidly developing individuals within brood (d(rapid)) and the standardized geometric mean fitness (GMF); standardization was done by dividing all GMF values by the largest value within the given simulation. The rows show results from simulations where the probability of good environmental state (p(good)) in each year was set to 0.25, 0.5, or 0.75 (top, middle, and bottom row, respectively). Columns represent the utilized bet-hedging (BH) strategies in the simulated populations, in which females used either exclusively static (left: a, d, g) or plastic (middle: b, e, h) bet-hedging, or both static and plastic bet-hedging females occurred in the population (right: c, f, i). Panels j–l show bet-hedging strategy differences in log GMF from simulated populations (p(good) set to 0.25, 0.5, or 0.75 for j, k, and l, respectively), where both static and plastic bet-hedging females occurred. Parameter estimates for the differences in log GMF between strategies and their confidence intervals are visualized on panel m
The value of p(good) (i.e. the probability that a given year will bring good environmental state) positively affected the optimal values of d(rapid), which is unsurprising: The more frequent good years are, the more worthwhile it is to have higher proportions of offspring that efficiently utilize beneficial conditions during good years, and ultimately yielding higher numbers of reproducing descendants. Higher probability of good years also had a substantial effect on relative reproductive success of static and plastic bet-hedging F0 females, as in more frequent good year scenarios the strategy-based difference in GMF grew larger, in favour of plastic bet-hedging females (Fig. 2m).
Some of the results seem to imply that, in the considered mortality patterns, at low (or zero) p(good), the highest GMF is expected at very low values of d(rapid), because if good years are very rare (or non-existent at all) then it is not quite beneficial for F0 females to partition their offspring to developmental types. On the other hand, when p(good) is high, values of d(rapid) close (or equal) to one will yield the highest GMF, because the fitness pay-off for having more rapidly developing offspring is substantially higher.
These dynamics might help explain why the number of simulations that conformed to the criterion of 0 < d(rapid) < 1 decreased so substantially with the increase of p(good): At high good year probabilities, most of the mortality patterns that met the four specified criteria likely lead to such GMF values among the most successful plastic bet-hedging females that were associated with d(rapid) = 1, while at low p(good) the highest GMFs were likely associated with d(rapid) = 0. Indeed, in an additional simulation run with p(good) set to 0.05, the number of simulations (where mortality patterns yielded 0 < d(rapid) < 1 for the largest GMFs) was 89 in the population where both static and plastic bet-hedging females occurred (which number is smaller than observed in simulations with p(good) = 0.25 or 0.5). In other words, optimal d(rapid) is dependent on p(good), and an optimal d(rapid) that is 0 < d(rapid) < 1 is only possible within an intermediate range of p(good) values.
Additionally, the higher the difference was in mortality of rapidly developing offspring between good and bad years, the larger GMF was for plastic bet-hedging females (Fig. 3). This trend, however, was not observed among static bet-hedging females.
Discussion
Altogether, the results suggest that cohort splitting in the wolf spider P. agrestis is likely an adaptive bet-hedging strategy on the part of early summer females, which enhances long-term (geometric mean) fitness in their unpredictably changing habitats. Partitioning the progeny into two developmental types appear to correspond to a diversified tracking scenario, i.e. diversification of offspring developmental phenotypes in order to decrease variance in short-term (single-generation) fitness, which ultimately leads to higher long-term fitness (Crowley and Hopper 2015). High random variations in environmental conditions, and in the reproductive success of developmental types, were described to favour the evolution of diversified bet-hedging strategies (Crowley et al. 2016; Crowley and Hopper 2015), which prerequisites appear to be met in the case of P. agrestis.
Not only is it supported by the presented theoretical investigation that cohort splitting is likely a bet-hedging strategy of early summer females, but results strongly suggest that females utilize plastic bet-hedging. As opposed to a static bet-hedging scenario, in which we would see fixed proportions of alternative developmental types within females (genotypes), in this plastic bet-hedging, we see that spiderlings only engage in rapid development when specific environmental criteria are met. But why would the effective reproductive success of F0 females be lower when cohort splitting occurs at both reproductive events throughout the yearly phenology? After all, the maximum number of offspring at t2 is the same in both static and plastic bet-hedging scenarios. A key factor here is likely that variation in survival is higher among the late summer (t1) spiderlings when there is cohort splitting, because of the differential mortality rates of the alternative developmental types in different environmental states. Also, since for late summer spiderlings no reproductive advantage could be realized before winter (i.e. both slowly and rapidly developing late summer spiderlings would reach maturity at around the same time, during early summer of the next year), no net gain is expected in the number of reproducing offspring at the next early summer (t2). Overall, modulating the proportion of rapidly developing spiders within the late summer brood decreases variance in effective reproductive success, hence leading to higher geometric mean fitness on the long run. In addition, while in natural populations there might be variation in whether or not rapidly developing spiderlings occur in the late summer (t1), based on the present modelling, one would expect that their proportion will remain close to zero in the population, as it provides the largest fitness pay-off (see Supplementary Fig. S2).
An important thing to note here is that, based on the results from the simulations, plastic bet-hedging appears to be a strategy practically always better than static bet-hedging. Indeed, the fitness gain of F0 females from early summer (t0) cohort splitting appears to be diminishing when cohort splitting also takes place during late summer (t1). In other words, with those mortality patterns used in the simulations, long-term (geometric mean) fitness will always be lower for females whose lineage has fixed cohort splitting because of increased variation in fitness; therefore, plastic bet-hedging should always be favoured over static bet-hedging. Bear in mind, however, that the mortality patterns used in the simulations are quite specific to P. agrestis, and other types of mortality patterns might contribute to the evolution of static rather than plastic bet-hedging. For instance, static bet-hedging may provide higher fitness pay-off in long term when the second cohort splitting (at late summer t1) would increase arithmetic mean reproductive success of F0 females, without substantially increasing variance in it (e.g. via lower mortality during t1 than during t0, see Supplementary Fig. S3). Therefore, while the simulations support that plastic bet-hedging is more likely in P. agrestis, the model of reproductive fitness based on which the simulations were done implicitly suggests that mortality patterns may exist that result in higher reproductive success for static bet-hedging.
Spiderlings may inherit different levels of propensity to take on rapid development when conditions, such as day length dynamics (reliably informing spiderlings about how much time they have left in the given season), are adequate. These are in accordance with previous results from empirical observations of spiderlings being responsive to environmental stimuli in their developmental plasticity. In adequate conditions, higher propensities translate to higher probability that any given offspring will take advantage of the favourable conditions, and by doing so greatly contributing to the fitness of its mother (and ultimately its inherited genotype, which it will pass onto its lineage). This propensity-based plasticity (also termed as sensitivity) is consistent with the generalist brood strategy (Frankenhuis et al. 2016), as it predicts variable responses between broods to the adequate stimuli on the part of offspring, which was indeed observed in laboratory rearing studies of P. agrestis. It might be worth noting that within-population variation in responsiveness to environmental stimuli may also be shaped by the stochastic nature of environmental state dynamics and weaker effect of natural selection on the short term on driving the evolution of the optimal proportion of rapidly developing spiders within broods. For example, genotypes of relatively low proportions of rapidly developing spiderlings will have higher effective reproductive success than genotypes characterized by the long-term optimal proportion of rapid spiderlings, when there are several bad years in a row. Furthermore, results from rearing tests show that even when environmental conditions are quite advantageous, not all spiderlings will develop rapidly, which is also in agreement with what one would expect to see when rapid development would be tied to some level of propensity. Such “fine tuning” of life history strategies by plasticity is known in plants (e.g. Sadeh et al. 2009), but empirical evidence remains elusive in the case of animals. Although current results do not constitute empirical evidence, future empirical studies designed on the basis of the findings reported here just might provide such evidence, and not only in P. agrestis. A prediction that can be drawn from the presented results in the case of P. agrestis is that propensity to take on rapid development in offspring is heritable, rather than average proportion of rapidly developing offspring within broods. Indeed, heritable reaction norms were found to be key in adaptive plasticity (Hutchings 2011). I propose that plastic bet-hedging in P. agrestis is likely in association with susceptibility genes (Aron et al. 2012; Belsky et al. 2009; Frankenhuis et al. 2016) shaping propensity to take on rapid development when adequate stimuli are present. If so, in future longitudinal studies using total pedigree of reared spiders, partitioning of phenotypic variance in developmental rate should enable us to differentiate between genetic, maternal, and environmental effects that shape development.
In diversified bet-hedging, it is expected that fitness of the alternative developmental types vary substantially between environmental states (Haaland et al. 2018, 2020). Results showed that in simulations of plastic bet-hedging higher mortality differences between good and bad years among rapidly developing spiderlings were associated with higher geometric mean fitness for the early summer females from which these spiderlings originated. Interestingly, in static bet-hedging simulations no such trend was observed, which might contribute to its lower fitness pay-off in comparison with plastic bet-hedging. Additionally, although not assessed in the current work, other mechanisms may also play an important role in shaping the fitness pay-off associated with different proportions of the alternative developmental types within broods. One such, which may be relevant in future studies on alternative developmental types arising from plastic bet-hedging, is negative frequency dependence. Indeed, this mechanism may play an important role in maintaining an intermediate proportion of rapidly developing spiders in P. agrestis, for example, by decreasing the strength of competition for resources within sub-cohorts (Christiansen et al. 1988; Post et al. 1997): Cohort splitting may help mitigate intra-specific competition by partitioning niches between sub-cohorts (Crowley and Hopper 2015).
As of yet it is unclear exactly what mechanisms play a role in controlling cohort splitting within broods (i.e. promoting during early summer, while suppressing during late summer), although, as outlined in the Introduction, photoperiod-dynamics appear to be central. Specifically, decreasing day length and lower temperatures may signal to late summer spiderlings that they are at the end of the season, when time and resources are expected to be insufficient to support rapid development. Also, while individual-level consequences of early summer cohort splitting were studied in detail recently (Rádai et al. 2020), autecological consequences of not taking on rapid development among the late summer spiderlings remain poorly understood. High energetic costs of rapid development may render it maladaptive to attempt to develop rapidly between late summer and next year’s spring, although currently it is not known what survival costs may be present during this time period in the phenology of P. agrestis. Furthermore, scarcity of food and low temperatures themselves may inhibit increased developmental rate (e.g. by their effects on metabolism: Brown et al. 2004; partly discussed in Rádai et al. 2017), promoting “safer” life histories that prioritize somatic maintenance over rapid development.
In conclusion, in the present theoretical investigation of the reproductive success of the wolf spider P. agrestis (relying on empirical observations), I found theoretical support for cohort splitting among early summer progeny being a bet-hedging strategy on the part of females from which this progeny generation originates. Indeed, female lineages producing an intermediate mix of developmental types within their broods were characterized by highest geometric mean fitness, especially when temporal variation in environmental quality was high. Supportingly, empirical observations show that there is low variation between females in the developmental characteristics of their offspring while within female variation is quite substantial. However, unlike in a static bet-hedging strategy, in which diversification of the offspring phenotype is expected to be probabilistic and fixed within females (genotypes), in P. agrestis, certain environmental stimuli have strong and consistent effect on the occurrence of the alternative developmental types within the broods. Based on empirical and theoretical results presented in this study, it is quite likely that early summer females of P. agrestis show a plastic bet-hedging strategy, in which their offspring might engage in rapid post-embryonic development when specific environmental stimuli are present. Also, when in simulated populations both static and plastic bet-hedging females reside, geometric mean fitness is considerably higher among those lineages utilizing plastic bet-hedging. I propose that such plasticity among the cohort splitting offspring is likely controlled by genes determining responsiveness to stimuli such as day length, and it is the offspring’s propensity to engage in rapid development in adequate conditions that is heritable, rather than the proportion of alternative developmental types within the brood. In future studies, P. agrestis may be an invaluable model organism in the study of the still poorly understood plastic bet-hedging on empirical grounds.
Data availability
Data used by Rádai et al. (2020) is deposited in Figshare (DOI: https://doi.org/10.6084/m9.figshare.9942533).
References
Aron EN, Aron A, Jagiellowicz J (2012) Sensory processing sensitivity: a review in the light of the evolution of biological responsivity. Personal Soc Psychol Rev 16(3):262–282. https://doi.org/10.1177/1088868311434213
Belsky J, Jonassaint C, Pluess M, Stanton M, Brummett B, Williams R (2009) Vulnerability genes or plasticity genes? Mol Psychiatry 14(8):746–754. https://doi.org/10.1038/mp.2009.44
Benton TG, Grant A (1999) Optimal reproductive effort in stochastic, density-dependent environments. Evolution 53(3):677–688. https://doi.org/10.1111/j.1558-5646.1999.tb05363.x
Bezanson J, Edelman A, Karpinski S, Shah VB (2017) Julia: a fresh approach to numerical computing. SIAM Rev 59(1):65–98. https://doi.org/10.1137/141000671
Brown JH, Gillooly JF, Allen AP, Savage VM, West GB (2004) Toward a metabolic theory of ecology. Ecology 85(7):1771–1789. https://doi.org/10.1890/03-9000
Christiansen FB, Antonovics J, Clarke BC, Partridge L, Robertson A, Clarke BC, Partridge L (1988) Frequency dependence and competition. Philos Trans R Soc Lond Ser B Biol Sci 319(1196):587–600. https://doi.org/10.1098/rstb.1988.0067
Crowley PH, Hopper KR (2015) Mechanisms for adaptive cohort splitting. Ecol Model 308:1–13. https://doi.org/10.1016/j.ecolmodel.2015.03.018
Crowley PH, Ehlman SM, Korn E, Sih A (2016) Dealing with stochastic environmental variation in space and time: bet hedging by generalist, specialist, and diversified strategies. Theor Ecol 9(2):149–161. https://doi.org/10.1007/s12080-015-0272-x
Einum S, Fleming IA (2004) Environmental unpredictability and offspring size: conservative versus diversified bet-hedging. Evol Ecol Res 6:443–455
Frankenhuis WE, Panchanathan K, Belsky J (2016) A mathematical model of the evolution of individual differences in developmental plasticity arising through parental bet-hedging. Dev Sci 19(2):251–274. https://doi.org/10.1111/desc.12309
Grantham ME, Antonio CJ, O’Neil BR, Zhan YX, Brisson JA (2016) A case for a joint strategy of diversified bet hedging and plasticity in the pea aphid wing polyphenism. Biol Lett 12(10):20160654. https://doi.org/10.1098/rsbl.2016.0654
Haaland TR, Wright J, Tufto J, Ratikainen II (2018) Short-term insurance versus long-term bet-hedging strategies as adaptations to variable environments [preprint]. Evol Biol. https://doi.org/10.1101/378091
Haaland TR, Wright J, Ratikainen II (2020) Generalists versus specialists in fluctuating environments: a bet-hedging perspective. Oikos 129:879–890. https://doi.org/10.1111/oik.07109
Hutchings JA (2011) Old wine in new bottles: reaction norms in salmonid fishes. Heredity 106(3):421–437. https://doi.org/10.1038/hdy.2010.166
Kiss B (2003) Autecology of the wolf spider Pardosa agrestis (Westring, 1861) [Doctoral dissertation, University of Veszprém]. http://konyvtar.uni-pannon.hu/doktori/2003/Kiss_Balazs_dissertation.pdf. Accessed 19 Feb 2019
Kiss B, Samu F (2002) Comparison of autumn and winter development of two wolf spider species (pardosa, lycosidae, araneae) having different life history patterns. J Arachnol 30(2):409–415. https://doi.org/10.1636/0161-8202(2002)030[0409:COAAWD]2.0.CO;2
Kiss B, Samu F (2005) Life history adaptation to changeable agricultural habitats: developmental plasticity leads to cohort splitting in an agrobiont wolf spider. Environ Entomol 34(3):619–626. https://doi.org/10.1603/0046-225X-34.3.619
Post JR, Johannes M, McQueen DJ (1997) Evidence of density-dependent cohort splitting in age-0 yellow perch, (Perca flavescens): potential behavioural mechanisms and population-level consequences. Can J Fish Aquat Sci 54(4):867–875. https://doi.org/10.1139/f96-335
Rádai Z, Kiss B, Samu F (2017) Effect of weather conditions on cohort splitting in a wolf spider species. J Arachnol 45(3):444–447. https://doi.org/10.1636/JoA-S-17-008.1
Rádai Z, Németh Z, Barta Z (2018) Sex-dependent immune response in a semelparous spider. The Science of Nature 105(7):39. https://doi.org/10.1007/s00114-018-1568-7
Rádai Z, Kiss P, Nagy D, Barta Z (2019) Antibacterial immune functions of subadults and adults in a semelparous spider. PeerJ 7:e7475. https://doi.org/10.7717/peerj.7475
Rádai Z, Kiss J, Babczyńska A, Kardos G, Báthori F, Samu F, Barta Z (2020) Consequences of rapid development due to cohort splitting: just how costly is to hurry? J Exp Biol 223:jeb219659. https://doi.org/10.1242/jeb.219659
R Core Team (2018) R: A language and environment for statistical computing (version 3.5.2). [computer software] R Foundation for Statistical Computing, Vienna. http://www.R-project.org/
Roff D (2002) A framework for analysis. In: Life History Evolution. Sinauer Associates Inc., pp 13–91
Sadeh A, Guterman H, Gersani M, Ovadia O (2009) Plastic bet-hedging in an amphicarpic annual: an integrated strategy under variable conditions. Evol Ecol 23(3):373–388. https://doi.org/10.1007/s10682-007-9232-2
Samu F, Szinetár C (2002) On the nature of agrobiont spiders. J Arachnol 30(2):389–402. https://doi.org/10.1636/0161-8202(2002)030[0389:OTNOAS]2.0.CO;2
Schaefer M (1977) Winter ecology of spiders (Araneida). Z Angew Entomol 83(1–4):113–134. https://doi.org/10.1111/j.1439-0418.1977.tb02381.x
Scheiner SM (2014) Bet-hedging as a complex interaction among developmental instability, environmental heterogeneity, dispersal, and life-history strategy. Ecol Evol 4(4):505–515. https://doi.org/10.1002/ece3.951
Simons A (2011) Modes of response to environmental change and the elusive empirical evidence for bet hedging. Proc R Soc B Biol Sci 278(1712):1601–1609. https://doi.org/10.1098/rspb.2011.0176
Starrfelt J, Kokko H (2012) Bet-hedging—a triple trade-off between means, variances and correlations. Biol Rev 87(3):742–755. https://doi.org/10.1111/j.1469-185X.2012.00225.x
Tuljapurkar S (1990) Delayed reproduction and fitness in variable environments. Proc Natl Acad Sci 87(3):1139–1143. https://doi.org/10.1073/pnas.87.3.1139
West-Eberhard MJ (2003) Developmental plasticity and evolution. Oxford University Press
Westring N (1861) Araneae svecieae. Göteborgs Kongl Vet Handl 7:1–615
Acknowledgements
I owe thanks to Zoltán Barta for his suggestions on the fitness-modelling approach, and two anonymous reviewers for their constructive and stimulating insights on the manuscript. On the figure of phenology, spider silhouettes were created using Stefan Sollfors’ original image of P. agrestis.
Funding information
Open access funding provided by ELKH Centre for Ecological Research.
Code availability
Julia codes are available at GitHub (https://github.com/zradai/Julia/tree/master/Paragr_plasticBH_MathMod).
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
ESM 1
(HTML 887 kb).
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Rádai, Z. Cohort splitting from plastic bet-hedging: insights from empirical and theoretical investigations in a wolf spider. Theor Ecol 14, 9–21 (2021). https://doi.org/10.1007/s12080-020-00475-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12080-020-00475-6