Introduction

Studying the evolution of a consumer facing a trade-off in consuming two resources has a long tradition (Levins 1963; Lawlor and Maynard Smith 1976; Wilson and Yoshimura 1994; Abrams 1986; 2006a,c; Egas et al. 2004; Rueffler et al. 2006, 2007). Theory on systems without oscillations suggests that the outcome of evolution depends on the shape of the trade-off: A weak trade-off should lead to the evolution of a generalist, whereas a strong trade-off should give rise to two specialists (Abrams 1986; Egas et al. 2004; Rueffler et al. 2006; 2007).

Table 1 List of parameters used in the model
Full size table

Although according to the principle of competitive exclusion, no more than n species can coexist on n resources; this is well known to be false for nonequilibrium systems (Armstrong and McGehee 1976, 1980; Huisman and Weissing 1999; Levins 1979). Wilson and Yoshimura (1994) showed that, in a two-habitat model for specialization, fluctuations in resource abundance can lead to a trimorphic state with two specialists and a generalist. However, their model does not include evolutionary change in the herbivores. Egas et al. (2004) included evolution and concluded that the evolution of all three types was possible, but under very restricted scenarios.

Their model does not include plant dynamics, however. For a full picture of the possible outcomes, both consumer and resource dynamics should be considered. Abrams (2006c) used a consumer-resource model with explicit dynamics for both consumers and resources. Contrary to the findings of Egas et al. (2004), this model does result in the coexistence of all three types, driven by fluctuations in resource abundance. These results were confirmed with an evolutionary model (Abrams 2006a), which found gradual evolution leading to the coexistence of a generalist with two specialists, both for endogenous and exogenous sources of variation. Evolution gives rise to one generalist when the trade-off for herbivores is weak, to two specialists when it is strong, and to all three when it is intermediate.

Even this study still has some limitations. Most importantly, like all others, it assumes that the two resources do not interact (apart from apparent competition if they share consumers): There is no direct competition or facilitation between the two resources. However, when we interpret the consumers and resources as, e.g., herbivores and plants, respectively, there are a large number of potential interactions. Plants may compete over space, over light, over water or plants; conversely, they may facilitate one another, e.g., by preventing evaporation or shielding from herbivores. All of these may impact plant dynamics and, by that, the course of evolution in herbivores.

In this study, we modified the model used by Abrams (2006a) to consider the evolution of herbivores on two plant species competing over nutrients, a well-established factor limiting plant growth (Elser et al. 2007; Howarth 1988; Vitousek and Howarth 1991). Competition between plants should lead to antiphase oscillations in plant abundance (Vandermeer 2004). These oscillations may lead to the evolution of trimorphism in herbivores, as is the case in Abrams (2006a); but it may also cause different evolutionary dynamics altogether.

To study this, we used a combination of two methods. Because the inclusion of competition makes the system no longer analytically tractable, we used numerical procedures to study the course of evolution. First, we used simulations to track the evolutionary change in herbivore preference through time. Second, we used pairwise invasibility plots (PIPs) to look for the existence and position of evolutionarily stable strategies and branching points, to confirm the results of the simulations.

Methods

Model setup

We used a simulation model with two plants, adapted from Abrams (2006a,b). We incorporated competition into the model by assuming a fixed and finite nutrient pool. Nutrients are utilized by plants, whose growth rate is limited by the amount of nutrients available. Because they use the same nutrients, this leads to indirect competition between plants. Nutrients are recycled into the system and become available again to plants through plant and animal death, and through consumption of plant material not digested by the herbivores, making the system an entirely closed loop.

The plants were completely equivalent in all our simulations: Their growth rate, dependence on the available nutrients, and their nutritional value to the herbivores are equal. They only differ in a trait that affects the preference of the herbivores, but does not directly affect their vital rates.

Ecological dynamics

The ecological dynamics of the system are determined by a system of differential equations, adapted from Abrams (2006a,c). Plant and herbivore dynamics are described by the following equations:

$$ \frac{{{\text{d}}{P_i}}}{{{\text{d}}t}} = \left[ {r\frac{{F(t)}}{{F(t) + T}}\frac{1}{{{c_p}}} - {d_P}} \right]{P_i}(t) - \sum\limits_{{j = 1}}^{{{N_H}}} {{C_{{ij}}}\left( {{P_i},{H_j},{x_{{ij}}}} \right)} $$
(1)
$$ \frac{{{\text{d}}{H_j}}}{{{\text{d}}t}} = e\frac{{{c_P}}}{{{c_H}}}\sum\limits_{{i = 1}}^{{{N_i}}} {{C_{{ij}}}\left( {{P_i},{H_j},{x_{{ij}}}} \right)} - {d_H}{H_j}(t) $$
(2)

Here, P i and H i are plant and herbivore biomass, respectively, and F is the amount of (free) nutrients available to plants. r is the intrinsic growth rate; T is the total amount of nutrients in the system; d P and d H are the per capita death rates for plants and animals, respectively; c P and c H denote the conversion factors between nutrients and plant or animal biomass; e is the conversion efficiency (the proportion of nutrients in the consumed material that is converted into herbivore biomass); C ij denotes the consumption of plant i by herbivore j, and is given by

$$ {C_{{ij}}}\left( {{P_i},{H_j},{x_{{ij}}}} \right) = \frac{{a{P_i}(t)x_{{ij}}^n}}{{1 + {t_h}a\left( {\sum\limits_{{i = 1}}^{{{N_P}}} {{P_i}(t)x_{{ij}}^n} } \right)}}{H_j}(t), $$
(3)

where a is the Holling type II functional response (Holling 1959), using the same trade-off structure as Abrams (2006a); x ij is the preference, or the proportion of the total time herbivore j spends feeding on plant i, where the two values must sum up to 1. This assumes a direct trade-off in the rate of attack on the two plant species: Time spent feeding on one plant species cannot be spent on feeding on the other. A herbivore with x = 1 is completely specialized on plant 1, whereas x = 0 means complete specialization on plant 2. In this trade-off, n is the coefficient that determines the shape of the trade-off; n < 1 gives a concave trade-off where generalists have the highest fitness, whereas n > 1 gives a convex trade-off, where the more extreme phenotypes have an advantage and specialization is favored. n > 1 is required for any other evolutionary outcome than only generalists; this appears to be a reasonable assumption (O’Hara Hines et al. 2004).

The dynamics of the pool of available nutrients are given by the following equation:

$$ \frac{{{\text{d}}F}}{{{\text{d}}t}} = {c_P}\sum\limits_{{i = 1}}^{{{N_P}}} {{d_P}{P_i}(t) + {c_H}\sum\limits_{{j = 1}}^{{{N_H}}} {{d_H}{H_j}(t) + \left( {1 - e} \right){c_P}} \sum\limits_{{i = 1}}^{{{N_P}}} {\sum\limits_{{j = 1}}^{{{N_H}}} {{C_{{ij}}}} } - \sum\limits_{{i = 1}}^{{{N_P}}} {r\frac{{F(t)}}{{F(t) + T}}{P_i}(t)} } $$
(4)

The nutrient pool is replenished by death of plants and herbivores (first and second term) and consumed plant biomass that is not converted into herbivore biomass (third term), and it is depleted when plants take up nutrients for growth (fourth term).

Setup of the simulation and evolutionary dynamics

Given the complexity of all the interactions, the above model is not analytically tractable. We therefore used simulations to study the result of this interplay between ecological dynamics and evolution. Herbivores are represented in the simulation as a large number of lineages (typically 400), each interacting with the two plant species. Each lineage has a value for x ij between 0 and 1; at the start of the simulation, their initial values are drawn from a normal distribution with a standard deviation of 0.1. In each timestep, the ecological dynamics of plants, herbivores, and available nutrients are determined by the above equations.

Evolution is simulated by allowing the lineages to “mutate”: Each timestep, each lineage has a small mutation probability. A mutation splits a lineage into two, spawning a daughter lineage and dividing its biomass between them. The preference value for the daughter lineage is drawn from a normal distribution around the parent value, with a small standard deviation (typically 0.01). The daughter lineage then takes the place of the lineage with the lowest biomass which goes extinct. The total number of lineages is thus constant throughout the simulation.

Simulations were run for 100,000 timesteps, after which the end result (what coalition of herbivores evolved) was recorded. We explored a range of values for three parameters very likely to affect the outcome of evolution: n, the trade-off coefficient, and r and T, plant intrinsic growth rate and total nutrients, because these will strongly affect plant abundances.

A total of eight different outcomes was found (including extinction of the herbivores) for a range of n, r, and T values: r ranged from 0.5–2; T ranged from, 2.5·106 to 6.5·106; and n ranged from 1.1 to 1.8 (a subset was run over a wider range, 1.0–3.6, to test whether the patterns also hold beyond this range). All parameter values can be found in Table 1.

Pairwise invasibility plots

To check the results of the simulations, specifically what happens after the herbivores reach the stage of generalist-specialist coexistence, we numerically generated a series of PIPs. To generate the PIPs, we used a simulation with the two plants and the two “resident” herbivores—a specialist (x = 0) and a generalist, whose value we varied from 0.5 to 1 by steps of 0.005. We first ran the simulation for 10,000 timesteps to allow the ecological dynamics to reach its final state, which was usually a regular pattern of oscillations in both plant and herbivore abundance. After this, we calculated the fitness of a mutant invading the system, averaged over several cycles. When oscillations were irregular, the fitness was averaged over 10,000 timesteps. The value of x for the mutant was varied from 0.5–1. We assumed the mutant biomass was zero because the mutant is rare.

Results

Most of the results of the timeseries follow the same pattern. At the start of the simulation, when plant abundances are equal, herbivores rapidly branch and evolve towards specialization because n > 1. The interaction between herbivores and plants then generates increasing asynchronous oscillations in plant abundances (Fig. 1a), changing the fitness landscape and increasing the fitness of generalists (Fig. 2a, b, solid line). The system temporarily reaches an unstable equilibrium when the herbivores are at the fitness minima, where the trade-off (driving them to specialization) and the oscillations (driving them to generalism) are exactly balanced. The only instance when this does not occur is when n is high enough for the herbivores to completely specialize before the oscillations become strong enough to lead to this intermediate stage.

Fig. 1
figure 1

Abundance of the two plant species over time, as herbivores become specialized. Solid line plant 1, dashed line plant 2. a Herbivores rapidly evolve partial specialization, ending up at x 1 ≈ 0.28 and x 2 ≈ 072 at t = 1,000; b equilibrium state with herbivores at x 1 = 0 (completely specialized on plant 2) and x 2 ≈ 0.64 (mostly specialized on plant 1). The parameters used are n = 1.3, r = 1, T = 4.5 × 106; c P  = 1; c H  = 2; a = 10−5; t h  = 0.1; e = 0.25; d P  = 0.05; d H  = 0.5

Full size image
Fig. 2
figure 2

Fitness landscapes at different temporal points in the simulation standardized so the highest fitness = 1. a t = 0, plant abundances are equal, and specialization is favored. b Solid line t = 1,000, oscillations lead to three fitness maxima, two for both specialists and one for the generalist strategy; dashed line t = 5,000, interaction between plant abundances and herbivore evolution gradually leads to a skewed fitness landscape with three fitness maxima, where the herbivores occupy the two leftmost maxima

Full size image

This intermediate state is known in adaptive dynamics as an evolutionary branching point (Geritz et al. 1998; Waxman and Gavrilets 2005): a strategy that is both convergence stable (so evolution will move towards it) and a fitness minimum, so mutants on either side can invade. If n is not high enough to have two specialists as its only ESS (see below), evolution always proceeds to this state. This is even the case if the herbivores start out as two specialists, or as two specialists and a generalist (results not shown).

Evolutionary branching will eventually take place in either or both of the herbivores, and what follows depends almost entirely on the strength of the trade-off. For low values of n (but still higher than 1), only the more generalist herbivores survive, and the end result is one generalist. For high values of n, only the more specialized branches survive, leading to two specialists.

The third, and more complicated, result arises for intermediate values of n. In this case, again a single branch of each herbivore survives, such that one herbivore evolves towards further specialization and the other towards a more generalist strategy. Which of the two herbivores becomes the specialist and which becomes the generalist seems random. Eventually, the herbivores evolve into one specialist and one generalist, where the specialist feeds exclusively on one plant and the generalist feeds on both, but has a (sometimes slight) preference for the other. The fitness landscape here is asymmetric and shows three maxima, with the herbivores occupying the two lowermost (see Fig. 2b, dashed line).

At this point, the interaction between herbivore evolution and plant abundances becomes the determining factor in the eventual result. There are seven possible outcomes from here, shown in Fig. 3. Two of these were expected, as they agree with the results of previous models (two specialists, and two specialists and a generalist), and one is somewhat trivial (extinction of herbivores). The other four, however, are novel outcomes. Two of these occur over almost the entire range for r and T (1 specialist and 1 generalist, Fig. 3b; 1 specialist and 1 cycling branch, Fig. 3d). The other two (cycling between two specialists and two generalists, Fig. 3g; and complete specialization with generalists repeatedly evolving and going extinct, Fig. 3h) are less common, but occur consistently for a part of the range of r and T.

Fig. 3
figure 3

The eight possible outcomes. a–f Most common ones, occurring over the entire parameter range: a one generalist (G); b one specialist and one partly specialized generalist (S-G); c two specialists and one generalist (S-G-S); d one specialist and one cycling branch, with a second specialist repeatedly evolving and going extinct (S-G/S); e two specialists (S-S); f extinction of herbivores (E). g, h Uncommon but consistent outcomes, found only for the combination of low r and intermediate-high T: g cycling between two specialists and two partly specialized generalists (S-S/G-G); h two specialists, with generalists repeatedly evolving and going extinct (S-S/G)

Full size image

Effect of n

Figure 4 shows the simulation results over the entire range for n, for two combinations of r and T (r = 0.5 and r = 1, T = 4.5·106). For these parameters, all eight possible outcomes occur; the pattern in which they occur over the range of n is representative for most other parameter values.

Fig. 4
figure 4

Summary of simulation results over a wide range of n, for T = 4.5∙106. a r = 0.5. b r = 1. Outcomes are as shown in Fig. 2. Each bar represents at least 100 simulation runs for 1.05 ≤ n ≤ 2.0; and at least 10 for n > 2.0. Simulations were run for 100,000 time steps, with mutation rate 0.05 and mutation step 0.01. Other parameters are the same as in Fig. 1

Full size image

From low to high n, the different outcomes occur in a typical pattern. For low n, the trade-off is not strong enough to favor specialization in the presence of oscillations; the result is one generalist (G). As n increases and specialization becomes possible, the next result is one specialist and one generalist (S-G), followed by the two evolutionary outcomes with three herbivores (two specialists and one generalist (S-G-S), and one specialist with one cycling branch (S-G/S), typically in this order). As n increases even more, the result is only two specialists (S-S), the trade-off being so strong that generalists cannot compete. Increasing n even further eventually leads to the herbivores going extinct (E), for two reasons. First, their dependence on their preferred plant becomes so strong that they cannot survive the oscillations. Second, eventually the trade-off becomes so strong that the herbivores go extinct before they can specialize.

These six are the outcomes that occur over the entire range for r and T. For a limited range (low r and intermediate-high T), two more outcomes occur (Fig. 3g–h). These are more uncommon and appear to be limited to this parameter range. In both cases, two complete specialists do evolve, but this is not a stable outcome and more generalist herbivores can invade, resulting in cycles in herbivore evolution. In the first case (S-S/G-G, Fig. 3g), after two specialists evolve, invasion of generalists occurs for both herbivores, until they again end up at the intermediate stage of two partly specialized generalists. From here, they evolve once more into two specialists, repeating the cycle. In the second case (S-S/G, Fig. 3h), typically occurring for higher n, generalists again invade, often on both sides, but eventually, they cannot compete with the specialists and go extinct, after which new generalists can evolve.

These simulation results can for a large part be explained by pairwise invasibility plots (Fig. 5). These show the course of evolution, assuming the S-G stage is reached. It is therefore limited to explaining only those cases that pass through this stage as an intermediate step (all except G and S-S, although it still makes clear when S-S is the only possible ESS). The PIPs show the evolution of the generalist, keeping the specialist fixed at x = 0.

Fig. 5
figure 5

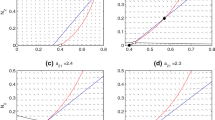
PIPs showing the fate of the second herbivore (starting out as generalist) once the S-G stage is reached; 0.5 = generalist, 1 = complete specialization. a–h r = 1, all other parameters the same as Fig. 3. Values for n are 1.3 (a)–1.65 (h) by steps of 0.05. a ESS with one specialist and one generalist; b–e ESS with one specialist and one generalist and branching point. The ESS is unstable in the long run as mutations can jump over the repeller, after which evolution will proceed towards the branching point; f branching point only; g–h ESS with two specialists. i–l r = 0.5. Values for n are 1.3 (i)–1.45 (l). i–j ESS with one generalist (though strongly biased towards specializing on the second plant) and one specialist; k branching point; l ESS with two specialists

Full size image

For low n, there is an ESS for S-G (Fig. 5a, i), with no other singular strategies. As n increases, two additional singular strategies arise: a repeller and, in the case of r = 1, an evolutionary branching point (Fig. 5b). Increasing n first leads to a narrowing of the distance to the repeller, making it possible for mutants to cross it and eventually to loss of the ESS altogether (progression shown in Fig. 5b–f). In these cases, evolution moves towards an evolutionary branching point (as seen in Fig. 3c–d). What happens after the branching point is reached is not discernable from the PIP; it can result in stable trimorphism (S-G-S, see Fig. 3c) or in cycling (S-G/S, Fig. 3d). In general, the former happens for the lower range of n, and the latter for higher values. Paradoxically, this means that as n increases, the specialist goes extinct in competition with the generalist. A possible explanation for this pattern is that, with increasing n, the resulting interactions between plants and herbivores become stronger, leading to stronger oscillations. This gives the generalist the advantage, allowing it to outcompete the specialist, after which the cycle starts again.

Increasing n even more, even the branching point disappears, and the system has only 1 ESS, for S-S (Fig 5h, l). In this range, only complete specialization can occur; the trade-off is too strong for the generalists to compete with the specialists.

Figure 5j–k gives some explanation for what happens with the two less common outcomes (Fig. 3g–h). Figure 5j corresponds to the S-S/G-G scenario: there is an S-G ESS at x ≈ 0.93, but the distance to the repeller at x ≈ 0.98 is small enough that mutations can cross it, leading to the S-S state. At this point, however, the exact same argument holds in reverse: Mutations can easily cross the repeller, making it easy for generalists to invade. The herbivores then end up once more at the fitness minima, after which the cycle starts again, leading to the pattern of Fig. 3g.

Figure 5k shows the S-S/G case. Here, there is an evolutionary branching point at x ≈ 0.93 and an ESS at x = 1 (two specialists), a pattern very similar to Fig. 5f (which leads to S-G/S). The difference is in the value for r, which is low and leads to smaller and slower oscillations. This makes it possible for the herbivores to completely specialize rapidly, skipping the intermediate stages described above. When the branching point is approached from below, as when r = 1 (and also a significant proportion of the simulations when r = 0.5), evolution proceeds as shown in Fig. 3c–e; but when starting at the extremes, this leads to the pattern shown in Fig. 3h. This explains why this result is only found for r < 1. This argument is supported by the fact that this outcome disappears when mutation rate is decreased and becomes increasingly frequent with increasing mutation rates. The same is true for the S-S/G-G outcome (results not shown).

Effect of r and T

The general pattern described in the previous section (which evolutionary outcomes are found, and the order in which they occur with increasing values for n) largely holds when varying r and T, two of the parameters most likely to change the plant dynamics, and thereby herbivore evolution. However, changing either r or T has a distinct effect on which outcomes are most likely to occur. Figure 6 shows the results over a narrower range for n (1.1–1.8) when r and T are varied. Several general patterns can be discerned:

Fig. 6
figure 6

Simulation outcomes depending on n, r, and T. Each graph has n on the x-axis and the proportion of each outcome on the y-axis; each bar represents at least 50 simulation runs. Parameters are the same as used in Fig. 1

Full size image

First of all, both increasing r and increasing T tend to result in stronger oscillations, and the total picture is roughly mirrored over the diagonal, with r and T having more or less equivalent effects. There is, however, also an interaction between the two parameters that makes the picture more complex.

Generalism is most likely to occur when oscillations are very strong—i.e., it becomes more frequent as either growth rate or nutrient availability increases. When both r and T have high values, generalism eventually becomes the only possible result. Complete specialization (S-S), on the other hand, is most likely for weak oscillations—when both growth rate and nutrient availability are low.

The most interesting interaction is found in the upper right and lower left corners: low intrinsic growth rate combined with high total nutrients or high growth rate with low nutrients. These two combinations both give a wide range over which evolution leads to the S-G outcome. As r or T (depending on which has the high value) moves further to the extremes, eventually this becomes the only possible outcome apart from G and S-S, and coexistence of more than two species becomes impossible. Conversely, coexistence of three herbivores (the two outcomes in Fig. 3c–d) is most likely when both r and T have low to intermediate values.

Finally, extinction usually occurs when the trade-off is strong (high n) and is most frequent under two conditions: first, when both r and T are very low (Fig. 6, upper left corner) because eventually plant abundance becomes too low to sustain the herbivore population, and second, when oscillations are very strong, i.e., with increasing r and T (see Fig. 7), because the (specialized) herbivores cannot survive the oscillations in their preferred food source. Extinction becomes less likely again when both r and T are very high, as the oscillations eventually become strong enough that specialists do not evolve at all.

Fig. 7
figure 7

Extinction rate as a function of r and T (extinction rate is the total extinctions for 1.1 ≤ n ≤ 1.8)

Full size image

Robustness of results

The model contains a number of simplifying assumptions. We took a closer look at several factors to determine how sensitive our results are to small changes in the model.

One obvious factor affecting plant dynamics is the shape of the plant growth function. To check whether this changes the results, we redid part of the simulations using several different growth functions. First, we used a ratio-dependent version of the growth function (Arditi and Ginzburg 1989; Abrams and Ginzburg 2000), where the amount of nutrient uptake depends on the available nutrients per unit plant biomass, rather than the absolute amount. The per capita plant growth then takes the following shape:

$$ g\left( {F,{P_1},{P_2}} \right) = r\frac{{a\left[ {F(t)/\sum\limits_{{i = 1}}^{{{N_P}}} {{P_i}(t)} } \right]}}{{b\left[ {F(t)/\sum\limits_{{i = 1}}^{{{N_P}}} {{P_i}(t)} } \right] + c}}, $$
(5)

which can be simplified to the more intelligible form

$$ g\left( {F,{P_1},{P_2}} \right) = r\frac{{F(t)(t)}}{{aF(t) + b\sum\limits_{{i = 1}}^{{{N_P}}} {{P_i}(t)} }}, $$
(6)

We used values of a = b = 1 for the extra parameters. Second, we used a modified version of standard Lotka–Volterra competition, with the difference that the amount of available nutrients takes the place of the carrying capacity:

$$ g\left( {F,{P_1},{P_2}} \right) = r\left( {1 - \frac{{\sum\limits_{{i = 1}}^{{{N_P}}} {{P_i}} }}{{F(t)}}} \right). $$
(7)

Both of these introduce an extra competition term, so that competition is both indirect (through depleting nutrients that the other species needs) and direct (by interfering with the other species’ nutrient uptake). The results of both were largely the same as the original version of the model. The same set of evolutionary outcomes occurs, in the same order and pattern over the range of 1.1 ≤ n ≤ 1.8. This suggests that it is not the specific growth function that determines the results, but the combination of the trade-off and the effect of competition in itself.

A second issue is the assumption that nutrients are returned to the environment upon death and immediately become available for uptake. In reality, all dead matter must be decomposed first before the nutrients can be of any use, introducing a time lag in the ecological dynamics. To determine whether this makes a difference, we constructed a version of the model that incorporates such a decomposition stage, which has various effects.

First of all, adding a decomposition stage essentially removes nutrients from the system, as they are caught up in decomposing matter; this effect becomes more pronounced as decomposition rate decreases. This is reflected in the patterns of evolutionary outcomes, which closely resemble those with lower total nutrients. This is not the only effect, however. The amount of nutrients caught in the decomposition stage is dependent on plant and herbivore abundances, and fluctuates over time. Depending on the rest of the ecological dynamics, it can either increase or decrease the amplitude of the oscillations in free nutrients, with consequent effects on plant dynamics. The effect of adding decomposition on herbivore evolution is therefore not straightforward, but it has no qualitative effect on the evolutionary outcomes that can occur.

Evidently, the way we included decomposition is very simplistic. Decomposition does not occur at a fixed rate, but is done by organisms that have their own ecological dynamics; furthermore, we assume that dead plant and animal biomass decompose at the same rate, but this is highly unlikely to be the case. Whether any of this would change the results merits further study.

A third major assumption is that the system is completely closed; the total amount of nutrients is constant, and there is no in- or outflow. We relaxed this assumption in two ways. First, we introduced random variation in the total amount of nutrients. Instead of being constant, at the start of each timestep, we drew the value for T from a normal distribution around the basic value (the change in nutrients was added to, or subtracted from, the pool of free nutrients). For the standard deviation, we used three different values (10,000, 100,000, and 500,000); only the third caused any significant deviation from the original pattern, and only when either r or T is low (making the effect of the fluctuations relatively more severe). The only significant change is that complete specialization becomes more frequent and occurs for lower values of n.

Second, we introduced some nutrient inflow and outflow, relaxing the assumption that the system is entirely closed. Inflow was assumed to be constant, whereas the amount of outflow was a proportion of the free nutrients in the system (typically a few per cent or less). The effects of this change are more complicated and resemble the effects of adding decomposition to the model. This is because the amount of outflow depends on the plant and herbivore dynamics, thereby adding a new level of complexity to the ecological dynamics. But as with decomposition, we find little qualitative difference in the evolutionary outcomes found, provided in- and outflow are low.

Finally, the eventual outcome of evolution depends on the interplay between ecological and evolutionary dynamics; the speed of evolution relative to the ecological dynamics is therefore important. We used a standard “mutation rate” (generation of new lineages) of 0.05, but to see what happens when the speed of evolution is changed, we varied the mutation rate from 0.001–0.1. In general, a lower mutation rate makes generalism more likely, as the herbivores have no time to specialize before the oscillations in plant abundance become prohibitively strong. This effect is most pronounced for high r and high T. Furthermore, the two outcomes limited to low growth rate (see Fig. 3g–h) disappear altogether if mutation rate becomes very low. Conversely, these two outcomes become more frequent as mutation rate increases. Furthermore, complete specialization (coexistence of only two specialists) is also more likely with high mutation rate, as this means that the herbivores can evolve into specialists before oscillations become very strong. Other than these, the results remain largely the same over the entire range for mutation rate.

Discussion

Our results show that adding nutrient competition to a simple consumer-resource model leads to results that are remarkably more complex than those found by previous models with a similar structure (Abrams 2006a,c; Egas et al. 2004; Rueffler et al. 2006, 2007). Like many previous models, we find that a weak trade-off leads to the evolution of a generalist, while a strong trade-off gives rise to two specialists. In addition, like Abrams (2006c), we find that only an intermediate trade-off strength, combined with asynchronous oscillations in resource abundance, leads to alternative coalitions of consumers. However, in addition to coexistence of two specialists and a generalist, we find four different evolutionary outcomes (plus extinction of herbivores): coexistence of one specialist and a generalist, and three types of cycling between generalist and specialist strategies.

The key factor causing the difference in the results lies in the addition of between-plant competition. While the previous models our work is based on (Abrams 2006a,c) explicitly look at the effect of endogenous cycles in resources, the effects of between-resource competition are more complicated than that. The extra interaction between the plants, in addition to their interaction through shared herbivores (apparent competition), makes the effect of herbivore evolution on plant abundance far from straightforward. Even without evolution, combining the effects of predation and competition can have more complex results than expected (Kotler and Holt 1989; Chase et al. 2002; Chesson and Kuang 2008). Added to this is the feedback with herbivore evolution, as it is the abundance of plants and the shape (amplitude and period) of their oscillations that drives herbivore evolution. To understand the outcome, it is therefore crucial to take into account the combined effect of all these interactions. For example, the asymmetric fitness landscape in Fig. 2b is an evolutionary endpoint, with the herbivores occupying the two lowermost maxima. Although it seems obvious from the fitness landscape that, at this point, herbivores close to the third maximum can easily invade, this is not necessarily the case. The simulations and the pairwise invasibility plots (Fig. 5a, i) both show that, for relatively low n, this state is in fact an ESS that cannot be invaded by specialists. If a specialist should evolve at this stage, its presence would affect the plant abundances, changing the fitness landscape in such a way that the third maximum would disappear and the new specialist would go extinct. Which types of herbivores can evolve in which coalition of existing ones depends on the interaction between plant growth (r and T) and the trade-off strength, as shown in Fig. 6.

One recent model (Zu et al. 2011) considers the evolution of predators on competing species; however, the authors find only a limited range of outcomes (a generalist, one specialist, two specialists, or two partly specialized generalists). Two of these are outcomes we do not find (one specialist and two partly specialized generalists; the former is simply impossible under the conditions of our model, and the latter we only encountered as an intermediate stage). We believe that this difference is probably due to their use of a linear functional response, rather than the more realistic type 2, or alternatively, to the way in which competition is implemented (Lotka–Volterra rather than nutrient competition). Which of these two is the more important factor remains to be seen, but it is certainly an interesting contrast to our own result and indicates that the role of between-resource competition is far from determined.

Some previous models about specialization have found a broader range of possible outcomes than the three found in Abrams (2006a), but all of these consider two consumer traits coevolving (coevolution with a behavioral trait, Rueffler et al. 2007; Abrams 2006b; coevolution with dispersal, Kisdi 2002; Nurmi and Parvinen 2011). Our model is the first to give such a diverse set of outcomes for only one evolving trait.

Besides the effect of n, the pattern of evolutionary outcomes also depends on the other two parameters studied, r and T. This is not surprising, given that these two parameters strongly affect plant growth, and in a roughly similar way: Higher values lead to oscillations with larger amplitude. This gives a greater advantage to generalists, essentially shifting the pattern of evolutionary outcomes to the right (Fig. 6); higher values for n are required to counteract the effect of the stronger oscillations and lead to the same evolutionary outcome. Conversely, low r or T leads to small oscillations, thereby shifting the pattern to the left. Thus, we see mostly complete specialization at the upper left corner of Fig. 6 (r and T both low), and mostly generalists towards the lower right (r and T both high). In practice, this would mean that we would expect to find specialists especially in nutrient-poor environments with harsh conditions (low temperature, rainfall, and sunlight), whereas generalists would be expected in nutrient-rich environments where conditions are favorable (high temperature, etc.). Whether these predictions of our model hold up is a subject for further study, although one recent review on plant–herbivore interactions and their response to global change (Massad and Dyer 2010) found that increases in temperature, CO2 and nutrients all increased consumption by generalist herbivores.

In the context of the evolution of generalists and specialists, there is some debate about the most common direction of evolution. Generalists are thought to be more likely to evolve into specialists than vice versa, both because specialists have less opportunity to diversify and because they are more likely than generalists to go extinct. Although phylogenetic studies seemed to confirm the assumption that the transition from generalist to specialist is more likely (Nosil 2002; Stephens and Wiens 2003), later studies have contested these results and concluded that generalists can evolve from specialists (Nosil and Mooers 2005; Stireman 2005).

If a strong trade-off favoring specialists exists, we may indeed expect the evolution of specialists; however, our results clearly show that this is not the whole story. Specialists can stably coexist with generalists (Fig. 3b, c); generalists can evolve into specialists and back again (Fig. 3g), and new specialists may repeatedly evolve and go extinct (Fig. 3d) while the same may be the case for generalists (Fig. 3h). There seems to be little reason to assume that evolutionary transitions can occur in one direction only.

Future directions

Although the results of this model are already quite complicated, the model still contains a large number of simplifying assumptions. The most important of these is that the two plants are completely equivalent, both in their interactions with each other and the environment (same growth and death rate, same dependence on nutrients) and their attractiveness and nutritional value to herbivores. We chose to do this because we wanted to focus on the effect of adding nutrient competition on the evolution of herbivores and chose not to include any other factors possibly affecting the direction of evolution. Furthermore, any differences between plants may affect competition between plants, complicating the results even further and making them difficult to interpret.

This assumption is likely violated in many real systems, and introducing differences between the plants in any of these traits might change the outcome. For example, if the plants have different growth functions, this will likely affect their ecological dynamics, possibly introducing much asymmetry from the start. How this will affect the evolution of the herbivores is unknown; it will probably not be straightforward and may strongly depend on the kind of differences that are assumed to exist between the plants.

Related to this, our model only looks at evolution from the herbivore’s point of view. However, the herbivores are not the only ones facing selective pressure; plants may be expected to evolve ways of coping with herbivory. Moreover, plants face a trade-off between defense against herbivores and competitive ability, especially if defensive strategies (e.g., structural or chemical) are costly (Herms and Mattson 1992), and rapid growth will come at the cost of being preferred by herbivores (Mattson 1980; Moran and Hamilton 1980; for a recent theoretical analysis of plant evolution under this trade-off, see Branco et al. 2010). How this will play out, and interact with the evolution of herbivores, is an open question.

One other limitation is that herbivore preference is entirely fixed. We define preference as the relative attack rate on plant species i, or the relative amount of effort the herbivore spends on plant species i. The actual amounts an herbivore consumes depends both on its preference and the relative abundances of each plant species; it will consume more of the more abundant plant species, unless it has evolved to be an obligatory specialist (x = 0 or x = 1). In this sense, actual diet is somewhat flexible and adapts to the circumstances, but there is still little room for adaptive behavior. Previous models have shown (Abrams 2006b; Rueffler et al. 2007; Carnicer et al. 2008) that allowing for adaptive consumer behavior can have a significant effect on the outcome of evolution and coexistence. This could potentially increase the number of evolutionary pathways and endpoints even beyond what we find; alternatively, it could decrease them by stabilizing the cycles found in our results.

Lastly, we introduced competition into the model by using nutrient limitation. While realistic, this is far from the only possible form of interspecific competition. Considering other forms of competition (e.g., over space, light or water), or facilitation (e.g., by preventing soil erosion or water evaporation), in addition to nutrient competition, may give rise to even more complex results.