Introduction

In conservation biology, and in ecology in general, it is important to correctly understand the causes of increased risk of extinction. Accordingly, estimates of temporal fluctuations in population density are essential because they constitute a major factor determining the persistence of a population (e.g., Inchausti and Halley 2003). The mix between variance and mean has a marked impact on the extinction risk and is often measured as the coefficient of variation. Still, temporal fluctuations have other properties that may influence the probability of extinction, one of which is autocorrelation. Several investigations of natural abiotic and biotic time series have shown positively autocorrelated variation referred to as red noise (Steele 1985; Pimm and Redfearn 1988; Pimm 1991; Halley 1996; Inchausti and Halley 2002; Vasseur and Yodzis 2004). In theoretical and empirical studies, the autocorrelation in time series of population densities is usually measured using a spectral representation obtained by applying a Fourier transform. The spectral representation of a time series without any autocorrelation has an equal mixture of all inherent frequencies, and it is termed white noise in analogy to white light. A time series that is (positively) autocorrelated is dominated by low frequencies and is denoted red noise. In theoretical studies, either autoregressive (AR) or spectral methods are used to generate colored time series of environmental noise, and the environmental noise is included in models of population growth that generate fluctuations in population densities. Most investigations of noise affecting population fluctuations use models in which noise acts on carrying capacity or growth rates. Previous general conclusions (Ruokolainen et al. 2009) indicate that an increased autocorrelation (i.e., reddening of noise) decreases the extinction risk when dynamics are over-compensatory, but increases the extinction risk when dynamics are under-compensatory (e.g., Ripa and Lundberg 1996; Petchey et al. 1997; Cuddington and Yodzis 1999). One of our aims here was to ascertain whether these conclusions are valid when populations exist in a spatial context.

Synchrony in the dynamics of spatially subdivided local populations is an important phenomenon. Population synchrony is often measured as a cross-correlation (Bjørnstad et al. 1999), and an increased degree of synchrony increases the extinction risk (Heino et al. 1997; Kendall et al. 2000; Liebhold et al. 2004). Environmental noise can synchronize population dynamics through the Moran effect (Heino et al. 1997), and this can be enhanced by the reddening of the noise color, at least when there is a strongly reddened noise (Heino et al. 1997; Heino 1998). Environmental noise can also by itself be more or less synchronized and thereby affects the extinction risk. Any set of environmental noise can be characterized by both its synchrony and its color, and thus the degree of synchrony across space and the noise color are interrelated. Generating environmental noise for a spatial setting entails a risk of introducing large variability in noise color and, for example, unintentionally changing the color when altering the synchrony and vice versa (Vasseur 2007). There are a few techniques that can generate noise with both explicit color and synchrony. Vasseur (2007) proposed a spectral method for a two-patch system which is too complicated with partnering phases to directly extend to a several-patch system. Ruokolainen and Fowler (2008) have presented an AR method that includes a more appealing equation, but is only applied in a food web context and not in a spatial context. A similar approach to the one presented here was conducted by Petchey et al. (1997) where they investigated the effects of noise color on extinction risk in a spatial setting. They used an AR method to generate noise and added variance to separate local carrying capacities to capture spatial heterogeneity. If the variance of the carrying capacities across space is zero, the time series of the local carrying capacities are all the same and, hence, completely synchronized. Yet, when variance increases, the time series will become dissimilar and the synchrony decreases. The spatial heterogeneity will then reflect a different degree of synchrony, although synchrony was not explicitly measured or tested. Petchey et al. (1997) showed that the effects of noise color was the same as of a non-spatial system when there was no spatial heterogeneity (i.e., increased reddening decreases the extinction risk when population dynamics is over-compensatory), but when there was spatial heterogeneity, related to unsynchronized environmental noise, the effects of reddening were the opposite and instead increased the extinction risk. These results propose that the effect on extinction risk includes an interaction between synchrony and the color of environmental noise. The approach by Petchey et al. (1997) focused on spatial heterogeneity and not synchrony. They also studied global colored noise affecting local patches rather than the effect of local noise color. Here, we focus on synchrony and local noise color. Therefore, we present a spectral technique using a 1/f method, related to the one described by Vasseur (2007), to generate noise while maintaining good control over local noise color, variance, and mean, combined with control of synchrony between the time series. To relate our work to the study by Petchey et al. (1997), we make a thorough comparison of the two methods, especially spatial heterogeneity and synchrony versus noise color.

In a review concerning colored noise in ecological and evolutionary dynamics, Ruokolainen et al. (2009) concluded that the effects of noise color are the same in a spatial setting as in a non-spatial setting, if population dynamics are under-compensatory. However, this conclusion cannot apply to the spatial study conducted by Petchey et al. (1997) because that work did not include under-compensatory dynamics, nor is it fully relevant to the investigation by Gonzales and Holt (2002) which modeled a two-state process (switching between two environmental values). To contribute to the overall understanding of the impact of colored noise both in a non-spatial and a spatial setting, our goal here was to reanalyze such settings over a larger parameter interval and larger sets of population dynamics while explicitly handling synchrony. In short, here, we examine both over- and under-compensatory dynamics where noise is affecting the carrying capacity or (indirectly) the growth rates, for a larger noise color interval, and we achieve this by using 1/f noise instead of an AR method. Thus, we have two objectives: (1) to present a reliable noise-generating method that controls for both the noise color and synchrony of systems with more than two time series and (2) to fill in the gaps in the knowledge about how noise color in a spatial setting affects single-species models. Our work is motivated by the need to extend the basic knowledge of how environmental noise influences (single-species) population dynamics in a spatial setting before attempting to study more complicated systems, such as those comprising several species, distance-dependent spatial synchrony, or explicit configurations of the landscape.

Methods

A novel method for generating noise in a spatial context

To generate the environmental noise, we use 1/f noise where the time series are produced by summing sine waves of different frequencies (f). The squared amplitudes (A) of the waves (the periodogram) follow a power law and are proportional to 1/|f|γ:

$$ {\rm periodogram} (f) = {A^2}(f) \propto 1/{\left| f \right|^{\gamma }}\quad { }f \ne 0 $$
(1)

The value of the spectral exponent γ indicates the noise color, and we use a general notation where “red noise” is γ > 0, “white noise” is γ = 0, and “blue noise” is γ < 0 (blue noise is not included in our study). Hence, instead of using distinctions of “pink noise” (γ = 1), “brown noise” (γ = 2), and “black noise” (γ = 3), we use “red noise” for all γ > 0. The amplitudes and phases of the corresponding frequencies for a specified γ are used to construct a set of vectors, where each vector represents a fast Fourier transform (FFT) of a real-valued time series (Cuddington and Yodzis 1999; Halley et al. 2004). In the FFT, half the elements consist of complex conjugates of the other half, the amplitude of the zero frequency of each time series is the mean of the time series (Eq. 6), and the amplitudes of non-zero frequencies scales to the standard deviation of the time series (Eq. 5). Before a vector can be inverse-transformed to achieve the real-valued time series, we also have to assess the phase of each of the frequencies. The signal (of length L for patch j) in the spectral representation can then be calculated using the phase θ and the amplitude A:

$$ FX_j{(k)} = {A_{{k,j}}}{e^{{i{\theta_{{k,j}}}}}}\quad k = 0, 1 \ldots \left( {L - 1} \right) $$
(2)

The real-valued time series ε t,j are calculated as the inverse FFT of (FX):

$$ {\varepsilon_{{t,j}}} = \sum\limits_{{k = 0}}^{{L - 1}} {{{{\rm FX} }_j}(k){e^{{2\pi kt/L}}}} \quad t = 0,1 \ldots \left( {L - 1} \right) $$
(3)

were t denotes time. The generated noise ε t,j can then be used in the population models (“Applying the novel noise method in a spatially implicit model”).

The phases of the sine waves are used to assess the synchrony between time series (Vasseur 2007). A phase of a frequency moves the sine wave of the frequency along the time axis, at most 2π units. If two time series with the same frequencies and amplitudes also have the same phases, the two will be perfectly synchronized and actually identical (but this will not be the case here because we add small variations to the amplitudes; see “Calculation of amplitudes, phases, and synchrony”). The phase of a specific frequency is set in two steps: first, a common random number for all time series, rand f , is picked from the uniform distribution on the interval [0, 2π]; thereafter, a specific random number, rand f,j on the interval (1 − ρ)[0, 2π], is added to each of the time series (Eq. 7). This second step differentiates the phases between the time series by the parameter ρ. When ρ = 1, all time series are almost the same (see “Calculation of amplitudes, phases, and synchrony”) and fully synchronized; when ρ = 0, the phases are random between time series, and hence the time series becomes fully independent.

We use pairwise cross-correlation (Bjørnstad et al. 1999) as the measure of generated synchrony between the time series of patches. The relationship between ρ used when generating a time series (Eq. 7) and the measured cross-correlation ρ* of the generated noise is not perfectly linear. Although not necessary, we correct for this; hence, ρ in Eq. 5 is changed slightly to give requested ρ* values. Figure 2 shows the input and measured values of synchrony with correction included in the generating of noise.

Calculation of amplitudes, phases, and synchrony

In this section, we are more specific about the method and present calculations and equations of amplitudes, phases, and synchrony. For even more details, see the MATLAB code in the Electronic supplementary material Appendix A. We construct a time series of length L with mean m, standard deviation σ, and noise color γ for each local patch j. Let A k,j denote the amplitude corresponding to frequency f = k/L and M = (L − 1)/2. Then, the amplitudes are calculated in three steps:

$$ \begin{array}{*{20}{c}} {{A_{{k,j}}} = \left( {c/{{\left| k \right|}^{{ \frac{\gamma }{2} }}}} \right){e^{{{\beta_{{k,j}}}}}}}{k = 1,2 \ldots M} \\ {{A_{{k,j}}} = {A_{{L - k,j}}}}{k = \left( {M + 1} \right),\left( {M + 2} \right) \ldots \left( {L - 1} \right)} \\ \end{array} $$
(4)

Some minor variation (not necessary to include, yet, more realistic) between the time series is created with the random numbers β k,j ; here, we use Gaussian random numbers from a distribution with μ = 0 and σ = 0.01. The constant c is used to scale the amplitudes to get the requested standard deviation and is calculated as:

$$ c = \frac{\sigma }{{\sqrt {{\sum\limits_{{k = 1}}^{{L - 1}} {{A_{{k,j}}}^2} }} }} $$
(5)

The amplitude of the zero frequency is set to the mean:

$$ {A_{{k = 0}}} = m $$
(6)

The phase θ k,j of the frequency number k and patch j is calculated by

$$ \begin{array}{*{20}{c}} {{\theta_{{k,j}}} = {{{\rm rand} }_k} + {{{\rm rand} }_{{k,j}}}\quad k = 1,2, \ldots M} \\ {{\theta_{{k,j}}} = - {\theta_{{L - k,j}}}\quad \quad \quad \quad \;k = \left( {M + 1} \right),\left( {M + 2} \right), \ldots \left( {L - 1} \right)} \\ {{\theta_{{0,j}}} = 0} \\ \end{array} $$
(7)

where rand f and rand f,j are random numbers from the uniform distribution on the intervals [0, 2π] and (1 − ρ)[0, 2π] respectively. In his method called “phase partnering,” Vasseur (2007) used a constant phase shift between the frequencies of two time series to achieve the desired degree of synchrony and used a “coin toss” procedure to shuffle the “leading” and “lagging” of frequencies. The procedure, presented here, will randomize all inherent frequencies of all generated time series; thus, no problems of “leading” and “lagging” of time series will occur (Vasseur 2007).

Method performance and comparison with a previous technique

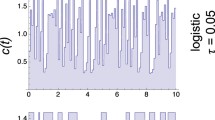
Some analyses of the generated noise are presented in Figs. 1 and 2. It can be seen that synchrony has no effect on the linearity of the power spectra (Fig. 1) or on the means or the variances of the measured color γ* (Fig. 2), and noise color has no effect on the means of the measured synchrony ρ*. The variation between replicates of ρ* shows a small increase with increasing γ (Fig. 2b).

Fig. 1
figure 1

Five time series unsynchronized (ρ = 0.1) (a) or synchronized (ρ = 0.9) (b) with noise color γ = 1.8. The corresponding power spectra are shown (c, d). Dots are overlaid implying consistent power spectra across patches. γ and ρ are input values, and γ* and ρ* are the measured output values of noise color and synchrony, respectively. The degree of synchrony does not affect the color or the power spectra

Full size image
Fig. 2
figure 2

Generating noise: comparing input with achieved values. γ and ρ are input values, and γ* and ρ* are the measured output values for noise color and synchrony, respectively. The generated noise is a set of ten time series of length = 1,000; synchrony is calculated as pairwise cross-correlation (Bjørnstad et al. 1999). Variation (replicates = 500) is shown as error bars of one standard deviation (although not clear for some results due to too small variations)

Full size image

Earlier results concerning the effects of noise color on extinction risk in a spatial context have been summarized in a review published by Ruokolainen et al. (2009). In the part of that review related to our study, the findings were based mainly on an investigation conducted by Petchey et al. (1997), where they studied the effects of colored noise and spatial heterogeneity on population persistence time. Since spatial heterogeneity, modeled as a variance among local carrying capacities, was updated each time step, the time series of local carrying capacities were synchronized according to the degree of spatial variance. Thus, not directly focusing on it, Petchey et al. (1997) still handled synchrony, and thus we need to relate our work to theirs. Petchey et al. (1997) used an autoregressive method (AR(1)) to generate noise:

$$ {\varphi_{{t + 1}}} = \alpha {\varphi_t} + \rho {\varepsilon_t} $$
(8)

where α is the autocorrelation parameter (the analogue to γ), ρ is a parameter controlling the variance, and ε t is a Gaussian random number. For 0 < α < 1, the noise is positively autocorrelated (i.e., red noise), and this corresponds to 0 < γ ≈ 1.5 in our study. When Petchey et al. generated spatial heterogeneity, they used a value (K t ) for each time step from a generated time series with a specified autocorrelation (Eq. 8, applied to the carrying capacity K) as a mean of a Gaussian distribution from which they picked values for each local time series. To increase the spatial heterogeneity, i.e., decrease synchrony, Petchey et al. increased the standard deviation σ of the Gaussian distribution. Thus, the standard deviation σ has an effect on the synchrony between the time series; no variance generates exactly equal time series, while increasing the standard deviation makes the time series more dissimilar and less correlated. When the synchrony was decreased in this way, a white noise was added to the local time series. Thus, the less synchrony, the more white noise was added, and asynchronous local red noise time series were not as red as those with less standard deviation, which can be seen in Fig. 3. Also, adding this white noise increased the variance of the local time series. Converting the σ values used by Petchey et al. into pairwise cross-correlation shows that they only covered the interval of ρ ≈ 0.65 to ρ = 1. Our novel method can provide better control over local noise color (compare Figs. 2a and 3) and is also in agreement with synchrony measures like pairwise correlations.

Fig. 3
figure 3

Noise generated by the AR method suggested by Petchey et al. (1997) comparing input with the achieved values. Input values are noise color α and spatial heterogeneity σ. γ* is the measured output of noise color (calculated with a spectral method). The time series of local carrying capacities were used to calculate synchrony between patches, an alternative to the spatial heterogeneity measure. Synchrony ρ was calculated as a cross-correlation. Dashed lines show the values that will be obtained if the spatial heterogeneity/degree of synchrony has no effect on the output noise color at a local level. The noise is generated for a set of ten time series

Full size image

Applying the novel noise method in a spatially implicit model

We performed simulations in which we used the well-known Ricker model to describe population dynamics. In line with Petchey et al. (1997), we changed from over- to under-compensatory (i.e., from oscillatory to monotone) dynamics by changing the parameter b:

$$ {N_{{t + 1,j}}} = {N_{{t,j}}}{e^{{r\left( {1 - {{\left( {{N_{{t,j}}}/{K_{{t,j}}}} \right)}^b}} \right)}}} $$
(9)

where r is per capita rate of increase, N t,j is the population density, and K t,j is the carrying capacity of patch j at time t. The mean value of K t,j over time was set to K m  = 100, and the initial population density for each subpopulation was N 0,j  ∼ N(K m /2, K m /8). Population sizes below 1 were set to zero. The length of the time series was 1,000, and there were 500 replicates. The range of b in a Ricker model is from 0 to 1; here, we used b = 1 and b = 0.1 to give over- and under-compensatory dynamics, respectively. The model described a spatially subdivided population (i.e., a metapopulation) consisting of a number of local subpopulations (n = 10). We modeled the landscape implicitly, and the dispersal was as simple as possible. In line with Petchey et al. (1997), the dispersal was density-independent, and a fixed proportion (d = 0.1) of emigrating individuals had the same probability of reaching all patches in the landscape, i.e., it was a global dispersal process (also often denoted mass-action mixing): d ij  = d/n was the proportion of the total population at patch i dispersing to patch j. Dispersal occurred first, then reproduction, and finally census. Inasmuch as the dynamics also could be influenced by the growth rate r, we ran simulation setups for three values of r (0.4, 0.8, and 1.2), which we chose to avoid cyclic and chaotic dynamics.

Environmental variation ε (see “A novel method for generating noise in a spatial context”) entered locally, either in carrying capacity K (as indicated by Ruokolainen and Fowler 2008) or affecting the realized growth rate (as described by Kaitala et al. 1997 and similar to Ripa and Lundberg 1996). In all, we simulated three model cases: Case I with over-compensatory dynamics and noise affecting K:

$$ {N_{{t + 1}}} = {N_t}{e^{{r\left( {1 - {{\left( {{N_t}/K\left( {1 + {\varepsilon_t}} \right)} \right)}^1}} \right)}}} $$
(10)

Case II with under-compensatory dynamics and noise affecting K:

$$ {N_{{t + 1}}} = {N_t}{e^{{r\left( {1 - {{\left( {{N_t}/K\left( {1 + {\varepsilon_t}} \right)} \right)}^{{0.1}}}} \right)}}} $$
(11)

Case III with over-compensatory dynamics and noise affecting the realized growth rate:

$$ {N_{{t + 1}}} = {N_t}{e^{{r\left( {1 - {{\left( {{N_t}/K} \right)}^b}} \right)}}}\left( {1 + {\varepsilon_t}} \right) $$
(12)

The mean and standard deviations of environmental noise were set to m = 0 and σ = 0.625. For case III, we also tried a model setup suggested by Mutshinda and O’Hara (2010): N t + 1 = N t exp(r(1 − (N/K)) + ε t ). The qualitative results agreed with those obtained using Eq. 12. However, having the noise parameter in the exponential function led to a skewed distribution of growth, which gave an unrealistically fast growth of populations and yet slow decreases, and this in turn produced unrealistic density means that were much too large compared with the carrying capacity.

For each time step, we calculated the global population size as the sum of all subpopulations. Global population extinction was considered to have occurred when N was equal to zero for all local populations. Local populations were set to zero when density was below 1. The extinction risk was calculated as the proportion of extinct global populations out of all 500 replicates. Furthermore, we calculated the mean population density (i.e., the mean of global density over the time period) for all replicates, and we checked population variance in the same manner. The maximum length of the simulation T was 1,000 time steps. Demographic stochasticity was not included.

Results

We studied over- versus under-compensatory dynamics by changing the parameter b. Population responsiveness was also affected by the growth rate r; therefore, cases I and II represented a smooth transition from over-compensatory with a very fast response (case I, r = 1.2) to under-compensatory with a very slow response (case II, r = 0.4), occurring via intermediate dynamics (case I, r = 0.4; case II, r = 1.2). The extinction risk decreased with increased γ for most of the over-compensatory dynamics (Fig. 4a, d). The progression from intermediate to low population responsiveness all showed hump-shaped effects of noise color on extinction risk (Fig. 4g, b, e, h), and finally, as in the first cases, there was a decreased extinction risk, but with steeper slopes for the slowest under-compensatory dynamics (Fig. 4h). The hump-shaped curve was visible only when environmental noise was unsynchronized (0 < ρ < 0.6). All three simulations (r = 1.2, 0.8, and 0.4) using over-compensatory dynamics and noise affecting the realized growth rate (i.e., case III) showed the same hump-shaped extinction risk with reddening noise (Fig. 4c, f, i). Also, the overall extinction risk increased with a decreased r in all three model cases.

Fig. 4
figure 4

Extinction risk as a function of noise color γ and (spatial) synchrony ρ among local patches (n = 10), shown for three different cases: over-compensatory dynamics and noise affecting K (Case I), under-compensatory dynamics and noise affecting K (Case II), and over-compensatory and indirect effects of noise on r (Case III), and for the following values of r (mean): 1.2 (top panels), 0.8 (middle panels), and 0.4 (lower panels). Local population dynamics followed the Ricker equation, with density dependence corrected for either over- or under-compensatory (i.e., oscillatory or monotone) dynamics. Extinction risks were calculated as the proportion of extinct replicates out of a total of 500 at the end of the simulated time period (T = 1,000). K mean = 100, and local patches were connected by global dispersal (d = 0.1). Environmental noise was generated by a two-dimensional FFT method

Full size image

The mean of population densities increased with increasing γ in all three cases (I, II, and III) independent of r (Fig. 5) and ρ (not shown), although there were steeper curves for larger r values (Fig. 5a, c). The variance of the population densities increased with increasing γ in all cases, independent of r; for high responsiveness (large r and over-compensatory dynamics), there was only a very minor increase, and for the lowest responsiveness (case II, r = 0.4), the increasing variance was more s-curved (Fig. 5d). Increased synchrony, ρ, did not change the effect of γ qualitatively, but did so quantitatively; increased ρ increased the variance of population densities because of the averaging effect of dispersal in unsynchronized populations. Note also that population variance increased markedly in case III when r = 0.4, and the corresponding population mean was larger than global K (1,000) for γ > 1, which is not realistic. These unrealistic behaviors were even more pronounced for under-compensatory dynamics when noise affected the growth rate; hence, we chose not to include that case in our study (see “A novel method for generating noise in a spatial context”).

Fig. 5
figure 5

Effects of spectral color of environmental noise on the mean (left) and the variance (right) of global population density in three different model cases. Case I, Over-compensatory (oscillatory) dynamics and noise affecting K. Case II, Undercompensatory (monotone) dynamics and noise affecting K. Case III, Over-compensatory (oscillatory) dynamics and noise affecting the realized growth. Synchrony of environmental noise was set to ρ = 0.4. There were ten subpopulations, r = 1.2, K mean = 100, and dispersal = 0.1 (mass-action mixing). Environmental noise was generated by a two-dimensional FFT method. Shading around the curves indicates 95% confidence intervals (in some cases, too small to detect)

Full size image

Discussion

Colored noise such as variation in resources or growth rates is an expected component of the population dynamics of natural communities (e.g., Steele 1985). Another component is the spatial aspect seen either as a set of patches (Gilpin and Hanski 1991; Kareiva and Wennergren 1995) or as a continuous landscape (Driscoll 2005). In this study, we introduced a novel method that combines these two components (time and space), and we also performed a detailed analysis of the effects of colored noise and synchrony. The most notable finding is that the effects of noise color on extinction risks did not interact with synchrony, which disagrees with earlier related results on noise color in a spatial context (Petchey et al. 1997). On the other hand, synchrony between patches had the most profound impact on extinction risk (i.e., always increased it), which does concur previous studies (Heino et al. 1997; Palmqvist and Lundberg 1998; Amritkar and Rangarajan 2006; Ruokolainen and Fowler 2008). Furthermore, as expected considering observations made by other investigators (Kaitala et al. 1997; Ripa and Lundberg 1996; Heino 1998), the effect of noise color was more intricate, but we present a straightforward way of interpreting this complexity, which is based on classical work by May (1981) and Roughgarden (1979). Both variances and means of densities have very simple relationships with the reddening of noise, regardless of inherent dynamics or synchrony between patches. The effect of noise color on the means and variances of densities are monotonic, and yet the dynamics and the way noise enters the model determine the extent to which means and variances will increase with reddened noise.

Studies by May (1981) and Roughgarden (1979) predicted that populations tend to average over high frequencies and track low frequencies of environmental noise affecting K, which means that populations track red noise more closely than white. The tracking is also a function of the responsiveness (i.e., the growth rate r; Roughgarden 1979); populations with small r tend to average over the fluctuations, while populations with large r track environmental noise more closely (May 1981). As a consequence of the increase in responsiveness to K (i.e., increased r), or increased reddening of noise, the variance in population density increases (Roughgarden 1979). Moreover, the relationship between r and noise color is such that due to increased reddening, the rise in variance is largest for intermediate r values (Fig. 20.6 in Roughgarden 1979). In our study, population responsiveness was affected by both r and the parameter b (over- or under-compensatory dynamics), and thus we used responsiveness ranging from slow [under-compensatory dynamics (case II, r = 0.4)] to high [over-compensatory (case I, r = 1.2)]. Intermediate responsiveness included the cases in between: under-compensatory when r = 0.8 and 1.2 and over-compensatory when r = 0.4 and 0.8 (probably under-compensatory, r = 1.2; overlapping over-compensatory, r = 0.4). Our results did show an increase in population variance with increasing γ (Fig. 5), and as predicted, the magnitude of the increase leveled off for the most responsive dynamics (over-compensatory, r = 1.2). A smaller increase was not observed in the slowest case (under-compensatory, r = 0.4), probably because it was still close to the intermediate r value zone for which the largest increase occurs (Fig. 20.6 in Roughgarden 1979) due to slight differences in the population models. We also noted an increase in population mean density with increasing γ in all cases, with the steepest slope for the less responsive dynamics (Fig. 5a, c). There was no clear increase in density mean with reddened noise in the studies conducted by May (1981) and Roughgarden (1979), although it was to some extent indirectly evident in those investigations; for example, Figure 2.8 published by May (1981) shows that lower growth rates resulted in a population that was markedly reduced and distinctly below the mean of K compared with the case involving a higher growth rate and less tracking error. Accordingly, our results concerning population variances and means are in accordance with previous classical observations and are also relevant in a spatial setting, even though dispersal in more unsynchronized populations levels off the differences between local patches and thus decreases population variance. Still, the degree of synchrony has no qualitative influence on how variances and means of population density are affected by the reddening of noise. Considering the effects on extinction risk, we observed a hump-shaped response to an increased reddening of noise for intermediate dynamics (Fig. 4). This can most likely be explained by the two counteracting forces: an increased population mean (decreasing extinction risk) and an increased population variance (increasing the extinction risk). Clearly, there is a chance that these two forces will result in an initial rise to the maximum extinction risk followed by a decrease (when the mean has reached sufficiently high levels). Of course, such an effect depends on the parameter intervals and other specifics, although the indicated chance ought to be greatest when there is a large increase in either of these parameters, and this appeared for the intermediately responding cases in our study.

The results for our case III (noise affecting growth rates as suggested by Kaitala et al. 1997 and similar to Ripa and Lundberg 1996) showed the same effects of responsiveness seen in the other cases, namely, both means and variances increased with reddened noise and the extinction risks showed hump-shaped curves (Figs. 5 and 4c, f, i). The results demonstrating that case III did not differ from our other two cases agree with some earlier observations (Ripa and Lundberg 1996). These findings were expected since the two approaches we used relied on the same responsiveness (caused by growth rates and degree of compensatory dynamics) to the difference between population density and carrying capacity.

In support of our interpretation, our qualitative results may hold, given that the system is governed by stable dynamics (because inherent oscillatory or chaotic regimes may alter the results; Kaitala et al. 1997). Thus, given these dynamics and findings, we argue that for low to intermediate responsive dynamics, there may very well exist a hump in extinction risk with increasing reddened noise. Populations with rapid responsiveness (i.e., over-compensatory dynamics or a large r) may not show this hump since the variance in population densities does not increase with reddened noise. The hump is also visible, yet not discussed, in the work of Cuddington and Yodzis (1999). They mainly studied the effect of black noise and made a comparison between 1/f noise and AR noise; still, there are hump-shaped results (but upside down since they calculated the mean persistence time instead of the extinction risk) for under-compensatory dynamics (Cuddington and Yodzis 1999; Fig. 2a). Schwager et al. (2006) also found a hump and argue that it arises due to the under-compensatory dynamics being more sensitive to extremely low successive values, which, in their AR noise, occurred more frequently for intermediate noise colors. The occurrence of consecutive similar values (e.g., extremely low values) is part of the nature of red noise. We feel that it is more reasonable to suppose that the hump-shaped response is better explained by the general effect of colored noise on the population means and variances. Although the results are not presented here, we also tested another plausible explanation, assuming that the variance of population density may not contain the important properties of the distribution of population densities. To that end, we checked the skewness and the shape of the distribution (e.g., see Lindström et al. 2008), but did not find any correlation between these two properties and extinction risks. Other related studies of the effects of noise on the extinction risk (e.g., Johst and Wissel 1997; Heino 1998; Heino et al. 2000; Mutshinda and O’Hara 2010) have not obtained any hump-shaped results within the spectral regions that were considered (e.g., often limited to the range of AR noise). These limited regions may explain why the cited studies (usually) found only the left or the right part of the hump. An investigation by Ripa and Lundberg (1996) nicely illustrated that the hump may shift along the axis, so it may even occur in blue noise region (a region most often not included).

Our results stress that there is no complex interaction between color and synchrony when it comes to the effect on extinction risk. This does not agree with the previous study of Petchey et al. (1997) that has shown that the effects of noise color differ markedly between synchronized and unsynchronized patches (i.e., homogeneous and heterogeneous landscapes). However, it is highly likely that the explanation for this discrepancy is that the earlier results were obtained using a noise-generating method focusing on global noise color and that unintentionally increased local variance and decreased reddening with increasing asynchrony (see “A novel method for generating noise in a spatial context”). According to our results, the general picture of noise affecting extinction risk in a spatial setting is that the difference between over- and under-compensatory dynamics is simply on a scale where an intermediate responsiveness raises the probability of a hump-shaped result with increasing reddening of noise. The spatial context, if focusing on local noise color, does not alter this general pattern, but it does determine whether or not the hump will be visible because the degree of synchrony affects the magnitude of the extinction risk. Also, our results support the idea that there are no qualitative differences between models in which noise affects the carrying capacity or growth rates r. An important issue that might be addressed in future studies is demographic stochasticity, which has an important impact on the extinction risk and to some extent may alter the effects of noise color (e.g., Ripa and Lundberg 1996; Petchey et al. 1997). It should also be mentioned that to obtain a clear understanding of how noise color affects extinction risks in a spatial context, we added an implicit landscape and hence also an extremely simplified dispersal rule. From an empirical point of view, this may appear to be a special case scenario with very limited application. However, from a theoretical perspective, we need some sort of baseline to understand more complex systems. Our results and methodology may become even more valuable as theoretical ecology proceeds with studies of noise color and synchrony that include interaction between species and more explicit landscapes.