Abstract
The neutral theory of biodiversity and biogeography emphasizes the importance of dispersal and speciation to macro-ecological diversity patterns. While the influence of dispersal has been studied quite extensively, the effect of speciation has not received much attention, even though it was already claimed at an early stage of neutral theory development that the mode of speciation would leave a signature on metacommunity structure. Here, we derive analytical expressions for the distribution of abundances according to the neutral model with recruitment (i.e., dispersal and establishment) limitation and random fission speciation which seems to be a more realistic description of (allopatric) speciation than the point mutation mode of speciation mostly used in neutral models. We find that the two modes of speciation behave qualitatively differently except when recruitment is strongly limited. Fitting the model to six large tropical tree data sets, we show that it performs worse than the original neutral model with point mutation speciation but yields more realistic predictions for speciation rates, species longevities, and rare species. Interestingly, we find that the metacommunity abundance distribution under random fission is identical to the broken-stick abundance distribution and thus provides a dynamical explanation for this grand old lady of abundance distributions.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Understanding the assembly and biodiversity of ecological communities is the primary aim of community ecology. In an excellent minireview of ecological assembly rules, Belyea and Lancaster (1999) summarized the main drivers or constraints determining community structure: environmental constraints, dispersal constraints, internal dynamics (such as competition), and biogeography (which includes the processes of speciation and extinction). Most of the literature in the past decades has focused on the first three factors (see, e.g., Cody and Diamond 1975; Weiher and Keddy 2001). In contrast, biogeography and the processes of diversification have received relatively little attention despite the pioneering work by MacArthur and Wilson (1967), Collwell and Winkler (1984), and Ricklefs (1987) who clearly showed the importance of these processes for community composition and macro-ecological patterns. However, there has been a revived interest in the influence of biogeographical forces on community structure in the last decade due to two new developments. The first development is community phylogenetics, which studies evolutionary relationships between coexisting species (Webb et al. 2002; Cavender-Bares et al. 2009). The second is neutral community ecology, which suspends the role of species differences in order to create a null model that allows the study of factors other than asymmetrical species interactions such as dispersal and biogeography (Hubbell 2001). In this paper, we focus on the latter development and particularly on the impact of speciation on the shape of species abundance distributions.
Building on the classic works of MacArthur and Wilson (1967) and Caswell (1976), Hubbell (2001) introduced his neutral theory of community ecology that states that stochastic interplay between a few basic, ecological as well as macro-evolutionary, processes (speciation, birth, and death, and—on a local scale—dispersal) can explain general large-scale diversity patterns, such as species-abundance distributions (SADs) and species–area curves. The neutral theory as developed by Hubbell (2001) makes three basic assumptions: (1) individuals of different species are functionally equivalent (neutrality assumption), (2) the community size is constant (zero-sum assumption), and (3) speciation is comparable to mutation where each individual has an equal probability of producing mutated, i.e., speciated, offspring (point mutation assumption). While the neutrality assumption is at the heart of the theory, the other two assumptions are assumptions of particular model implementations of the theory, allowing for analytical expressions for diversity measures, rather than fundamental assumptions of the theory itself. A mismatch between observations and theoretical predictions can, in principle, be due to these additional assumptions and therefore cannot be immediately interpreted as calling for a rejection of the neutral theory as a whole (Etienne 2007).
The zero-sum assumption and the point mutation assumption are of a very different nature. It has been shown that models without the zero-sum assumption predict mathematically exactly the same equilibrium SAD as the model with this assumption (Etienne et al. 2007a; Haegeman and Etienne 2008; Conlisk et al. 2010). In contrast, alternatives to the point mutation assumption can predict very different SADs (Hubbell 2001; Etienne et al. 2007b; Allen and Savage 2007; Haegeman and Etienne 2009; De Aguiar et al. 2009). Indeed, Hubbell (2001) claimed that speciation would leave a signature on diversity patterns in the metacommunity (see also Mouillot and Gaston 2007). Therefore, a thorough analysis of neutral theory, or any theory of community assembly for that matter, requires the (quantitative) exploration of alternative modes of speciation, particularly those that are very different from point mutation. Hubbell (2001) proposed an alternative speciation mode that is the opposite of the sympatric point mutation mode which he dubbed “random fission” because speciation results from random splitting of populations which may be interpreted as mimicking allopatric speciation. Intuitively, it seems more reasonable than point mutation because the incipient abundance of new species is larger than a single individual (Allen and Savage 2007; Rosindell et al. 2010), and it is also more plausible than a fixed initial abundance, as assumed by Allen and Savage (2007). Hubbell (2001) stated that the equilibrium metacommunity SAD resulting from random fission speciation is a zero-sum multinomial, just like the local community SAD in the point mutation case—which was later called dispersal-limited (Etienne and Alonso 2005, 2007), or recruitment-limited (Jabot et al. 2008) multinomial—but he did not prove this mathematically. Ricklefs (2003) provided some approximate formulas for the total species richness in the metacommunity under random fission speciation, but so far, a full mathematical treatment has remained elusive.
In this paper, we provide the full sampling formula for the distribution of abundance in a local community that receives immigrants from a very large metacommunity described by random fission speciation. It is thus the counterpart of the sampling formula where the metacommunity is described by point mutation (Etienne 2005) and may be similarly extended to involve multiple samples (Etienne 2007, 2009a, b). The metacommunity SAD is clearly different from the zero-sum multinomial, in contrast to Hubbell’s conjecture. We use the new sampling formula to fit the random fission model to six large tropical tree data sets and compare it to the fit of the point mutation model. We end with a discussion of our results.
Model
We will first describe metacommunity dynamics, solve it for the stationary abundance distribution, and then derive expressions for (possibly dispersal-limited) local samples from this stationary distribution. We add the superscript “meta” to expectations and probabilities that refer to the metacommunity to distinguish them from expressions for samples, which we will denote by the superscript “smp”.
The master equation
We follow Hubbell (2001) in assuming a constant metacommunity size and denote it by J M. However, as in the point mutation model (Etienne et al. 2007a; Haegeman and Etienne 2008), this assumption is not essential for determining the equilibrium species abundance distribution because fluctuations of species abundances cancel out and yield an effectively constant community size, that is, a sharply peaked probability distribution for metacommunity size (Haegeman and Etienne 2010). We denote the abundance vector in the metacommunity by \(\vec{S}=(S_{1},S_{2},S_{3},\ldots ,S_{J_{\rm{M}}})\) where each component S n is the number of species with abundance n. We study the behavior of the probability \({\mathbb{P}}\) of this vector in time by writing down the so-called master equation for this vector \(\vec{S}\) which reads, in general (Haegeman and Etienne 2009):
where R is a matrix that contains the rates of transitions \(R( \vec{S},\vec{S}^{\prime })\) to go from a vector \(\vec{S}\) to another vector \( \vec{S}^{\prime }\). The master equation (Eq. 1) describes the dynamics of the species abundance distribution \({\mathbb{P}}\) as a function of time. This distribution contains much more information than just the expectation values \(\mathbb{E}^{\rm{meta}} (S_{n})\), used by, for example, Vallade and Houchmandzadeh (2003) and Volkov et al. (2003, 2007), which is just the first moment of this distribution (Vanpeteghem et al. 2008), as we will see below.
To specify the stochastic community model, one has to determine the matrix R of transition rates. For different models, the matrix R will have different elements. For the random fission model, there are two types of transitions, and the matrix R can be written as a sum of two parts: R = R DB + R S. The first part, R DB, describes a death event immediately followed by a birth event. In such a death–birth event, one individual dies (all J M individuals have the same probability to be the one that dies), and a second individual reproduces (all remaining J M − 1 individuals have the same probability to reproduce). Note that this is exactly the death-birth event of the point mutation model. If the first individual belongs to a species with abundance k and the second individual to a species with abundance i, the transition is to a vector \(\vec{S}^{\prime }\) that can be written in terms of vector \( \vec{S}\) as
which means that it differs from vector \(\vec{S}\) by having a reduction by one of species with abundances k and i and an increase by one of species with abundances k − 1 and i + 1 (the unit vector \(\vec{e}_{k}\) is one at position k and zero elsewhere). The corresponding element of the transition matrix \(R^{\rm{DB}}(\vec{S},\vec{S}_{k,i}^{\rm{DB}})\), for which we use the shorthand notation \(R_{k,i}^{\rm{DB}}(\vec{S})\), is given by
with μ the overall rate of death–birth events. Strictly speaking, the transition rate 3 is only valid for k ≠ i (see “Appendix 1” for the full derivation).
The second part of matrix R, denoted by R S, describes a speciation event. We describe a speciation event as in Hubbell’s (2001) random fission model: An individual is selected at random (all J M individuals have the same probability to be selected). Suppose that this individual belongs to a species with abundance k. Then this species splits into two species, the first with abundance i (where i < k) and the second with abundance k − i, where each fission has equal probability, i.e., each split (i,k − i) has probability \(\frac{1}{k-1}\). The transition is to a vector \(\vec{S}^{\prime }\) that can be written in terms of vector \(\vec{S}\) as
which means that it differs from vector \(\vec{S}\) by having one less species of abundance k and an increase in the number of species with abundances i and k − i. The corresponding element of the transition matrix \(R^{\rm{S}}(\vec{S},\vec{S}_{k,i}^{\rm{S}})\), for which we use the shorthand notation \(R_{k,i}^{\rm{S}}(\vec{S})\), is given by
with ν the overall speciation rate.
For comparison, in the point mutation model, the death–birth events are also governed by Eq. 3, but speciation only produces singleton species, that is, only transitions to i = 1 are allowed:
where δ 1(i) = 1 for i = 1 and 0 otherwise.
The master equation (Eq. 1) together with the transition rates 3 and 5 fully define the neutral model with random fission speciation. Rather than trying to solve Eq. 1 for the random fission model which seems impossible, we take an indirect route consisting of three steps. First, we derive an equation for the expected number of species with abundance n which we will denote by \(\mathbb{E}^{ \rm{meta}}({S}_{n})\). We can solve this equation exactly. This will illustrate the main properties of the random fission model, but cannot be used to fit the model to data. To the latter end, we need the full sampling formula for the abundance distribution of a local community connected via limited dispersal to a metacommunity governed by random fission speciation. The second step starts by proposing an Ansatz for the solution of Eq. 1 and show that it is consistent with the previously obtained exact expression for \(\mathbb{E}^{\rm{meta}}({S}_{n})\). The third and final step applies sampling theory (Etienne and Alonso 2005) to this Ansatz, assuming large metacommunity size, in order to formulate the full sampling formula.
Equation for the expected number of species with abundance n
The definition of the expected number of species with abundance n in the metacommunity, \(\mathbb{E}^{\rm{meta}}({S}_{n})\), is
It is straightforward (see “Appendix 1”), by taking time derivatives on both sides of this equation and using Eq. 1 to find the stationary expectation of the number of species with abundance n in the metacommunity:
with
It is easy to see that Eq. 8 can be computed numerically by first calculating all a i for i from J M down to 1 and then by calculating \(\mathbb{E}^{\rm{meta}}({S}_{n}) \) for n from 1 to J M.
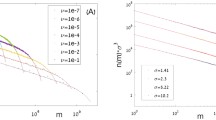
Note that these expressions only depend on J M and the ratio of ν and μ, that is, \(\frac{\nu }{\mu }\) which is the relative rate of speciation and birth–death events, similar to the point mutation model (Vallade and Houchmandzadeh 2003; Etienne et al. 2007a). Therefore, we will assume for simplicity of notation that μ = 1 without loss of generality. Figure 1 shows some numerical examples of \( \mathbb{E}^{\rm{meta}}({S}_{n})\) for various values of ν and J M.
Comparison of exact (Eq. 8, white) and approximate (Eq. 17a, black) predictions for the relative number of species in each abundance class, i.e., \(\mathbb{E}^{\rm{meta}}( \sum\nolimits_{n\in \rm{class }i}S_{n}) /\mathbb{E}^{\rm{meta}}( S) \). Abundance classes are defined on a logarithmic scale: the ith class being [2i − 1,2i), e.g., the first class contains abundance 1, the second class abundances 2 and 3, the third abundances 4, 5, 6, and 7, the fourth abundances 8 through 15 , etc. (Pueyo 2006)
So far, we have been able to provide exact solutions for the expectation values of S n for the stationary abundance distribution. Although these can be used for comparison to data after incorporating sampling, it does not allow full extraction of the information in a sample abundance vector \(\vec{S }\). For this, the full probability distribution, rather than just the first moment, is required. This full probability, called the sampling formula, enables one to extract information on individual species’ abundances as well as on their interdependencies. We therefore proceed to derive an extremely good approximation to this sampling formula. We can check the accuracy of this approximation by comparing the expectation value \(\mathbb{E}^{\rm{meta }}({S}_{n})\) computed using this approximation (and higher moments) to the exact solution for \(\mathbb{E}^{\rm{meta}}({S}_{n})\).
Ansatz for the probability of the metacommunity abundance vector \(\vec{S}\)
We start with an Ansatz which is justified elsewhere (Haegeman and Etienne 2010). Here, we only note that it is based on an approximation, for large J M, of the exact formulas 8 and below we will show numerically that it is an extremely good approximation for realistic values of J M and ν which justifies our use of it. The Ansatz is the following expression for the probability of the metacommunity abundance distribution \(\vec{S}\) given a fixed size J M:
where S M is the total number of species in the metacommunity and S k is the number of species with abundance k, both being stochastic variables as above (in contrast to \(\mathbb{E}^{\rm{meta}} ({S}_{n})\) and \(\mathbb{E}^{\rm{meta}}({S}_{\rm{M}})\) which are moments). The normalization constant Z(νJ M,J M ) is given by
where 1 F 1(a,b,x) is the confluent hypergeometric function and \(\binom{x}{y}=\frac{x}{y\left( x-y\right) }\) is the usual notation of the binomial coefficient. The second line is due to a classic combinatorial result,
From Eq. 9, we can derive (see “Appendix 2”) that
and that
Hence
Furthermore, we find that
This is a very interesting result because it corresponds exactly to the discrete version of MacArthur’s (1957) broken-stick model of the distribution of species abundances (see Etienne and Olff 2005)
Scaling limit
We consider the scaling J M→ ∞, ν→0 such that \(\sqrt{\nu }J_{\rm{M}}\) is finite. We call the quantity \(\sqrt{\nu }J_{\rm{M}}\) the fundamental biodiversity number in the random fission model and denote it by θ rf. We first study the distribution of the number of species S M. In the scaling limit, Eq. 12 becomes
with normalization constant Z(θ rf ) given by
where I α (x) denotes the modified Bessel function of the first kind for integer α and real-valued x; this is a standard mathematical function for which most mathematical software packages have numerical routines. Figure 2 shows that the mean and the mean ± 1 standard deviation of this distribution for S M as a function of J M almost coincide, indicating that the distribution is strongly peaked. This result can be obtained analytically; we refer to “Appendix 3” for the proof that, for large J M and large θ rf, the number of species S M is normally distributed with mean and variance equal to θ rf and \(\frac{\theta_{\rm{rf}}}{2}\), respectively. For any θ rf (but still in the limit J M→ ∞), we find that the expected number of species in the metacommunity is given by (see “Appendix 3”):
The expected total metacommunity richness as a function of metacommunity size for the random fission model (red) and the point mutation model (blue). Dashed lines indicate the variation in richness around the mean (±1 standard deviation). Mean and standard deviations are computed from the full probability distribution, Eqs. 29 and 30. The fundamental biodiversity constant is set at θ pm = θ rf = 1,000
The expectation values of S n ,S k S ℓ,...for large J M can then be derived (see again “Appendix 4” for the full derivation)
These approximations match exact numerical results for the random fission model outlined above very well. For example, Fig. 1 shows the extremely good match of the approximate expectations \(\mathbb{E}^{\rm{meta} }(S_{n})\) of Eq. 17a with the exact expectation given in Eq. 8. Similarly, the approximate second-order moments \(\mathbb{E}^{\rm{meta}}(S_{n}S_{m})\) of Eq. 17b are very close to the exact second-order moments \(\mathbb{ E}^{\rm{meta}}(S_{n}S_{m})\), solutions of Eq. 1 (results not shown). Because of this extremely good agreement, we believe that we can use the approximations with great confidence to explore the stationary properties of the random fission model.
For the derivation of our sampling formula for \({\mathbb{P}}\) below, we need the probability distribution for the relative abundance vector \(\vec{p}\). Equation 17 for large J M can be transformed in probability density functions \(\rho ^{ \rm{meta}}(p_{i}|S_{\rm{M}})\), \(\rho ^{\rm{meta}}(p_{i},p_{j}|S_{\rm{ M}}),...\) for relative abundances p i , p j ,... in the limit J M→ ∞ as follows: The probability that an individual belongs to a species having abundance p i J M is \(\frac{\mathbb{E }^{\rm{meta}}(S_{p_{i}J_{\rm{M}}}|J_{\rm{M}},S_{\rm{M}})}{S_{\rm{M} }}\). This probability becomes \(\rho ^{\rm{meta}}(p_{i}|S_{\rm{M}}) \mathrm{d}p_{i}\) in the limit J M→ ∞ (with \( \mathrm{d}p_{i}\sim \frac{1}{J_{\rm{M}}}\)). Therefore,
Likewise,
Continuing this procedure, we find that
Hence, all relative abundance vectors \(\vec{p}\) on S M species are equally probable. Note that densities 18a and 18b can be obtained from Eq. 18c by computing marginal distributions.
The results for the metacommunity are summarized in Table 1 where they can be compared with the results for the point mutation model.
Sampling formula \({\mathbb{P}}\) and sample expectations \( \mathbb{E}^{\rm{smp}}(S_{n})\)
The asymptotic formula 18c can be used to derive our central result, i.e., the dispersal-limited sampling formula (Alonso and McKane 2004; Etienne and Alonso 2005) for species abundances in a sample of size J from a dispersal-limited local community (parametrized by parameter I) that receives immigrants from a metacommunity undergoing random fission speciation (parametrized by parameter θ rf). The sampling formula gives the probability for the vector \(\vec{S}=(S_{1},S_{2},...S_{J})\), where each component S n denotes the number of species with abundance n, but it will be convenient to also use in our notation the abundance vector \(\vec{n} =(n_{1},n_{2},...,n_{S})\) where each component n i denotes the number of individuals of species i where the species are arranged in an arbitrary order. The detailed derivation of the sampling formula can be found in “Appendix 5”. Here, we mention the result (see also Eq. 42 in Table 2):
Here, the I with a subscript denote modified Bessel functions, and the I without a subscript denotes the dispersal limitation parameter. Furthermore, A = \(\sum\limits_{i=1}^{S}a_{i}\), a i just being an index for the summations in Eq. 33, S is the number of species in the sample, and S k is the number of species in the dataset that have abundance k. The \(\bar{s}(x,y)\) are the unsigned Stirling numbers of the first kind and (x) y is the Pochhammer symbol defined as
and the multinomial coefficient \(\binom{J}{\overrightarrow{n}}\) is defined as
For the expectation value we find (see “Appendix 6”):
which is Eq. 44 in Table 2. This expression uses the approximation to \(\mathbb{E}^{\rm{meta}}(S_{n})\). Using the exact formula would result in a much more complicated formula that is only negligibly different from the approximation (Fig. 1).
When dispersal is not limited (i.e., I→ ∞), then we have the random fission counterpart of the Ewens sampling formula (Ewens 1972). This formula is provided as Eq. 38 in Table 2. The associated expressions for the expected number of species with abundance n in the dispersal-unlimited sample is given in Table 2, as Eq. 40. Derivations can be found in “Appendices 4 and Appendix 5”. For comparison, Table 2 also shows the results for the point mutation model (Vallade and Houchmandzadeh 2003; Etienne 2005; Etienne and Alonso 2005) which has θ pm = ν pm J M where ν pm is the point speciation rate that is comparable to ν rf. Note that θ pm is often written as \(\frac{\widetilde{\nu }_{ \rm{pm}}}{1-\widetilde{\nu }_{\rm{pm}}}(J_{\rm{M}}-1)\) in the literature. In “Appendix 7”, we explain this difference, but here, we note that ν pm and \(\widetilde{\nu }_{\rm{pm}}\) are practically identical because they are very small and J M is very large.
Results
Random fission produces fewer abundant and fewer rare species, but more intermediately abundant species than point mutation with the same speciation rate ν (Fig. 3). When θ rf is set equal to θ pm, then random fission produces fewer abundant species than point mutation (Fig. 3). With our definition of θ rf, the SAD of a sample becomes independent of metacommunity size, only being dependent on the compound parameter θ rf. This is similar to the role of θ pm in the point mutation model. There is another similarity between the two θs as well: when increasing θ pm and θ rf, the abundance curves for point mutation and random fission shift in the same way to higher abundances (Fig. 3).
Comparison of the metacommunity SADs for random fission (Eq. 33, red) and point mutation (Eq. 24, blue) for various values of the speciation rate ν (top row) and fundamental biodiversity number θ (bottom row). Metacommunity size is set at J M = 300,000. The SADs are defined as the expected number of species per unit of logarithmic abundance with base 2. In formula, this means that we plot \( \mathbb{E}^{\rm{meta}}\left( S_{n}^{\prime }\right) =n\ln 2\times \mathbb{E }^{\rm{meta}}\left( S_{n}\right) \) on the y-axis and the log2 of abundance n on the x-axis
The total species richness in the metacommunity does not depend on J M in large metacommunities with random fission speciation (Fig. 2). In contrast, in a metacommunity with point mutation speciation, metacommunity size always controls total species richness. Figure 4 shows the behavior of the SAD in a metacommunity with random fission, as a function of recruitment limitation. When recruitment is severely limited, the SADs of the point mutation and random fission models are very similar, suggesting that the mode of speciation does not leave a noticeable signature on the SAD in recruitment limited communities, but it does when recruitment limitation does not play a role.
As an illustration of our new sampling formula, we applied it to six tropical tree data sets (Volkov et al. 2005). Table 3 shows the parameter estimates obtained by likelihood maximization. It also shows the results obtained previously (Chave et al. 2006; Etienne et al. 2007b) for the point mutation model and compares the two models based on Akaike weights. Figure 5 shows the abundance distributions with the fitted models. Clearly the model with random fission speciation never performs significantly better than the point mutation model. There are two cases where the performance is similar.
First, Korup has as maximum likelihood estimates an infinite θ and a very low m-value that corresponds to the Ewens estimate for I. This is the value of I that maximizes the Ewens sampling formula with parameter I (instead of θ); this value is well known to solve the equation:
where Ψ is the psi or digamma function (see also Eq. 32 for a similar expression). For Korup, which has S = 308 and J = 24591, this amounts to I = 49.5. When θ is infinite, the mode of speciation is no longer important: Every immigrant in the local community will be of a new species. This is indistinguishable from a metacommunity (ruled by point mutation) with θ pm = 49.5 (Etienne et al. 2006).
Second, for Sinharaja, the point mutation and random fission models perform equally well, remarkably with almost identical m-values (but different θ-values). This suggests more strongly that there is extreme recruitment limitation and metacommunity diversity is high, in contrast to the values reported by Volkov et al. (2005), who missed the slightly higher likelihood optimum for high θ and low m (Etienne et al. 2007b).
The random fission model does not seem to possess the dual optima exhibited by the point mutation model (Etienne et al. 2006). This is probably because the random fission sampling formula does not have the symmetry of the point mutation sampling formula where infinite θ and infinite I have mathematically identical effects. Figure 6 shows the likelihood surface of the random fission model for BCI.
Although θ rf and θ pm are not directly comparable because they are defined differently, their ratio tells us something about the relative values of the speciation rates in the two models:
For Yasuni, the ratio of θ pm and θ rf is the smallest of all data sets (approximately \(\frac{1}{54}\)) which means that ν rf < ν pm if ν pm < 0.0003. As values of ν pm larger than 0.0003 are highly unlikely, we can conclude that random fission must occur at a lower rate than point mutation to fit the observed SAD.
As a numerical example, assume that metacommunity size in the neotropics is of order \(J_{\rm{M}}\approx 10^{10}\) (Ricklefs 2003; Nee 2005). This means that, for Yasuni, the corresponding speciation rates are \(\nu _{\rm{pm}}\approx 10^{-8}\) and \(\nu _{\rm{rf} }\approx 10^{-12}\). The average species longevities are then (Ricklefs 2003) \(t_{\rm{pm}}\approx -2\ln (2\nu _{\rm{pm} })\approx 10^{2}\) and \(t_{\rm{rf}}\approx \nu _{\rm{rf}}^{-\frac{1}{2} }\approx 10^{6}\), and the expected total richness is \(\mathbb{E}_{\rm{rf} }^{\rm{meta}}(S_{\rm{M}})\approx 10^{4}\) (see Eq. 1) and \(\mathbb{E} _{\rm{pm}}^{\rm{meta}}(S_{\rm{M}})\approx \) 4·103 (see Eq. 1). We discuss these results below. Note that all these speciation rates are community speciation rates divided by community death–birth events (remember we assumed the latter to be μ = 1). For an estimate of the species-level speciation rates measured in inverse generations, these numbers need to be multiplied by the average population size \(\frac{J_{\rm{ M}}}{\mathbb{E}^{\rm{meta}}(S_{\rm{M}})}\).
We also fitted the metacommunity sampling formula to two data sets of metacommunity abundances. The first consists of 41 plots of 1 ha in Panama (Condit et al. 2002), and the second consists of 50 plots of 1 ha in the Western Ghats in India (Munoz et al. 2007; Etienne 2009a). We did the analysis in two ways. First, we simply pooled the data of all the plots into a single sample. Second, we sampled a single individual from each plot, recorded the number of species, repeated this many times, and estimated θ from the averaged number of species obtained (Etienne 2009a); loglikelihoods and Akaike weights were obtained by averaging over their values for each sample. The results are summarized in Table 4. In the first, “pooled sample”, analysis, the random fission model performed much worse than the point mutation model for both data sets. Yet, in the second, “repeated samples”, analysis, we find that the point mutation model performs only marginally better. We discuss this discrepancy below.
Discussion
In this paper, we have presented a full sampling formula for the SAD in the neutral model with random fission speciation, with and without recruitment limitation. In contrast to Hubbell’s (2001) conjecture, the metacommunity abundance distribution (i.e., without recruitment limitation) is not a zero-sum multinomial. In fact, we have shown that the random fission mode of speciation produces a SAD that is identical to the broken-stick model of MacArthur (1957), when conditioned on total metacommunity size and total metacommunity species richness. An expression for the SAD (i.e., \({\mathbb{P}}\)) for the discrete broken-stick (DBS) model was given in Etienne and Olff (2005), and this expression is mathematically identical to our Eq. 14. Our Eq. 18c is the continuous form of the broken-stick model (CBS), that is, in the limit of J M→ ∞. Thus, random fission speciation provides a mechanistic explanation of this classic broken-stick model. Indeed, random fission and random stick-breaking are equivalent processes mathematically, but is not immediately obvious that they lead to the same distribution because the random fission model includes ecological drift (random birth and death processes) whereas the broken-stick model is not clearly linked to biological processes.
Similarly, our dispersal-limited sampling formula can be interpreted as a dispersal-limited broken-stick model. Although the fits to data are not better than the point mutation model (which produces the logseries), adding dispersal limitation makes the fits much better than found by Etienne and Olff (2005) for the pure DBS model. We might therefore say that the broken-stick model has been resurrected to some extent from the natural death, so longed for by its inventor (MacArthur 1966). Cohen (1968) also showed that the broken stick could be produced by alternative models, but none of these were dynamical such as our birth–death-speciation model. The random fission model is also more general than these models because it also predicts an SAD without conditioning on total species number.
In contrast to another conjecture by Hubbell (2001), the metacommunity abundance distribution is not governed by two parameters (ν rf and J M), but by only one just like in the point mutation model. This parameter, the random fission fundamental biodiversity number, is defined as \(\theta _{\rm{rf}}=\sqrt{\nu _{\rm{rf}}}J_{\rm{M}}\). This definition of θ rf is different than that of θ pm by a factor of \(\sqrt{\nu _{\rm{rf}}}\). This explains why Hubbell (2001) thought that two independent parameters govern the random fission model: He found with his simulations that fixing ν rf J M did not fully determine the abundance distribution. Had he fixed \( \sqrt{\nu _{\rm{rf}}}J_{\rm{M}}\), then he would have found that the SAD was completely specified. Strictly, this is only true in the limit of large J M that we are considering, but in practice, this limit is always approximating the system extremely well.
We have compared the fit of the random fission model against the point mutation model in three different ways. First, we confronted six local community data sets with the dispersal-limited sampling formulas. We found that the random fission model never performed significantly better than the point mutation model and did much worse in several cases. However, this may be due to nonneutral recruitment limitation (Jabot et al. 2008) obscuring the comparison of speciation modes. We therefore also compared fits of the models to metacommunity data directly. Unfortunately, large metacommunity data sets, where individuals are randomly sampled across a large spatial scale, are scarce. At best, there are a limited number of local samples, e.g., 41 and 50 in the data sets we used here. Although we recognize that the sampling effort for these data sets is appreciable, these data sets require some restrictive assumptions in their analysis. Our second comparison consisted of pooling all the samples as if the individuals were randomly sampled rather than sampled in local clusters, thereby ignoring spatial structure. Here, the random fission model performed miserably. Our third comparison consisted of repeatedly sampling one individual from each plot and averaging results over all these small samples (of sizes 41 and 50), thereby ignoring that the data showed an actual metacommunity richness that was much higher than that of each of those samples. In this case, random fission and point mutation performed equally well. Remarkably, the maximum likelihood estimates for θ pm are roughly of the same order of magnitude for the pooled sample and repeated samples, whereas the estimates for θ rf are three-fold smaller in the repeated samples than in the pooled samples. This suggests that the random fission model does not produce the correct scaling with sample size and even more so because the sample size in the pooled sample is larger than a true metacommunity sample with the same number of species, due to recruitment limitation. Thus, we conclude that the point mutation model really seems a much better description of the metacommunity than random fission model. The relatively reasonable fit of the random fission model to some of the local community data sets is only achieved by allowing for strong (and arguably unrealistic) dispersal limitation which eradicates the signature of the speciation mode (recall Fig. 4).
Fitting a model to a single snapshot of species abundances is a weak test of the model (McGill 2003; McGill et al. 2006, 2007) because many different mechanisms may lead to similar patterns in SADs (Cohen 1968; Purves and Pacala 2005). However, it is a test that a serious model should pass. Not all models produce a realistic SAD and failure to do so is a strong reason to reject a model. Here, we have confirmed earlier findings (Etienne et al. 2007b) that SADs can have resolving power with respect to explanatory models, and particularly the speciation mode leaves a clear signature on the SAD (see Fig. 7, which will be discussed further below). We have shown that the random fission mode never performs significantly better than the point mutation mode; indeed, it performs much worse for almost all data sets and the metacommunity data sets in particular. This suggests that point mutation is a more likely mode of speciation in tropical forests than random fission. However, random fission predicts more reasonable speciation rates, metacommunity richness, and species longevities based on the fitted parameters. Perhaps the estimates for species richness seem somewhat high, suggesting that the metacommunity for the Yasuni plot is of the order of the entire Amazon, but such a continental extent of the metacommunity may be quite reasonable taking into account recent evidence for long-distance dispersal (Jabot and Chave 2009). Thus, neither of the two models is capable of making more accurate predictions of various quantities or patterns. For now, this leads us to reject both models in their current, spatially implicit, form as plausible explanations of community structure. We do want to caution against too rapid definite conclusions for the following reasons.
Metacommunity SADs (as defined in Fig. 3) for four different speciation modes: individual-level point mutation (Eq. 24, solid blue line), species-level point mutation (Etienne et al. 2007b, dashed blue line), individual-level random fission (Eq. 8/Eq. 23, solid red line), and species-level random fission (dashed red line). The solution for \(\mathbb{E}^{\rm{meta}}(S_{n})\) in the latter case is, like the individual-level random fission model, given by Eq. 8 but with \(s_{i}=\frac{\nu _{\rm{rf}}}{J_{\rm{M}}}\). Metacommunity size is set at J M = 100,000 and expected metacommunity richness is set at \(\mathbb{E}^{\rm{meta}}(S_{\rm{ M}})=\rm{1,000}\). Expected metacommunity richness is the area under the curve for all models because of our definition of the SAD: \(\int \mathbb{E}^{\rm{meta }}( S_{n}^{\prime }) d\log _{2}n=\int \mathbb{E}^{\rm{meta} }( S_{n}) n\ln 2\) \(d\log _{2}n=\int \mathbb{E}^{\rm{meta} }( S_{n}) dn=\mathbb{E}^{\rm{meta}}(S_{\rm{M}})\)
The performance of a model in producing realistic SADs depends on all ingredients of the model (Etienne 2007), not just the one under consideration, such as the speciation mode in this paper. We have studied the speciation mode in a neutral context, so the performance is also affected by the neutrality assumption. Random fission or point mutation or both may perform better or worse in a nonneutral setting, or even have negligible influence. Zillio and Condit (2007) have, however, found that many communities, neutral or non-neutral, are primarily driven by the process of how new species enter the community. In our opinion, this justifies our study of the influence of speciation in the simplest context where species differences do not play a role, but we do not rule out the possibility that the mode of speciation may lead to more or less realistic predictions under nonneutral conditions. Only by formulating different models and comparing their predictions to data can we get a feel for the behavior of these models and for how informative SADs are for inferring mechanism.
Speciation is not the only way new species can enter the community: Immigration is another. Interestingly, the sampling formula resulting from point mutation speciation also describes long-distance dispersal (see, e.g., Etienne et al. 2007a) which may leave a more profound signature than speciation. Only a model that includes both long-distance dispersal and speciation will be able to distinguish the relative contribution of these processes. An analytically tractable spatially implicit model with long-distance dispersal and random fission speciation is not yet available, let alone a spatially explicit model. Nevertheless, a spatially explicit neutral model with long-distance (fat-tailed) dispersal and point mutation speciation has been studied (Rosindell and Cornell 2009) using coalescence techniques (Rosindell et al. 2008). It has been shown that speciation rates required to yield predictions on species–area relationships that are in agreement with observations are much lower (i.e., more realistic) than in models with Gaussian dispersal kernels (Rosindell and Cornell 2007). This suggests that long-distance dispersal is an important force shaping ecological communities and can mimic the effect of speciation, but does not rule out that speciation still leaves a signature on community structure. Unfortunately, coalescence does not seem compatible with random fission speciation because random fission is not time reversible, and therefore, this powerful simulation method cannot be employed to further study the effect of random fission speciation on community structure in a spatially explicit context. Perhaps new analytical techniques based on functional differential equations (O’Dwyer et al. 2009) will prove useful.
Random fission assigns a very low probability to samples with a few very abundant species, even more so than point mutation. This explains why the fit to data is worse for the former speciation mode and the fact that the best fitted model does not seem to follow unimodal SAD data in some cases (even though the unimodal shape is more characteristic for random fission than for point mutation, see Figs. 3 and 4). Etienne et al. (2007b) pointed out that a visual goodness-of-fit estimate may be deceiving and logtransformed the data and predictions to make this clear. Here, logtransformation supports the same conclusion (not shown). At the same time, random fission predicts fewer rare species in the metacommunity than point mutation and therefore produces a more lognormal-like shaped SAD which is believed to be a better description by many ecologists (Preston 1948, 1962; McGill 2003). The fit to the metacommunity data sets suggests that this advantage does not offset the disadvantage at large abundances. In fact, this advantage may not be so advantageous after all because the random fission model even seems to predict too few rare species.
For Hubbell’s neutral models ν is a constant speciation rate per individual (for both point mutation and random fission), in contrast to common practice in speciation research where the speciation rate is usually a rate per species (Stanley 1979; Etienne and Apol 2009). The results in this paper apply to Hubbell’s model. Assuming a constant speciation rate per species in the neutral model with point mutation has also been studied (Etienne et al. 2007b), and it was found that this assumption can make a large difference. Therefore, the remaining combination of random fission speciation with a constant speciation rate at the species level appears to be a necessary last step to get a complete picture. In fact, while a constant speciation rate per individual seems a logical first choice for the individual-level process of point mutation, a constant speciation rate per species seems more obvious for the species-level process of random fission. The community will be less diverse than in the individual-level case because abundant species will be less likely to undergo fission. For the same reason, the species-level point mutation model produced less diversity than the individual-level point mutation model (Etienne et al. 2007a). Figure 7 shows a numerical comparison of all four speciation modes. One observes that species-level random fission is similar to individual-level random fission but has a bit more abundant and rare species. Because very abundant species are not only more likely than in individual-level random fission model but also than in the individual-level point mutation model (this can only be seen after logtransforming Fig. 7), it might be that a model with species-level random fission speciation provides a good fit to SAD data as well as reasonable predictions for speciation rates and species longevities. We have not been able to find a sampling formula for this model, so this remains an open question.
We have presented analytical results for the spatially implicit model with the random fission mode of speciation. These are now on a par with analytical results for point mutation, allowing future studies of community models to compare both alternatives.
References
Allen AP, Savage VM (2007) Setting the absolute tempo of biodiversity dynamics. Ecol Lett 10:637–646
Alonso D, McKane AJ (2004) Sampling Hubbell’s neutral theory of biodiversity. Ecol Lett 7:901–910
Belyea LR, Lancaster J (1999) Assembly rules within a contingent ecology. Oikos 86:402–416
Caswell H (1976) Community structure: a neutral model analysis. Ecol Monogr 46:327–354
Cavender-Bares J, Kozak K, Fine P, Kembel S (2009) The merging of community ecology and phylogenetic biology. Ecol Lett 12:693–715
Chave J, Alonso D, Etienne RS (2006) Comparing models of species abundance. Nature 441:E1–E2
Cody M, JM Diamond E (1975) Ecology and evolution of communities. Belknap, Cambridge
Cohen JE (1968) Alternate derivations of a species-abundance relation. Am Nat 102:165–172
Colwell RK, Winkler DW (1984) A null model for null models in biogeography. In: Strong LADR, Simberloff D, Thistle AB (eds) Ecological communities: conceptual issues and the evidence. Princeton University Press, Princeton
Condit R, Pitman N, Leigh EG, Chave J, Terborgh J, Foster RB, Nunez P, Aguilar S, Valencia R, Villa G, Muller-Landau HC, Losos, E, Hubbell SP (2002) Beta-diversity in tropical forest trees. Science 295:666–669
Conlisk J, Conlisk E, Harte J (2010) Hubbell’s local abundance distribution: insights from a simple colonization rule. Oikos 119:379–383
De Aguiar MAM, Baranger M, Baptestini EM, Kaufman L, Bar-Yam Y (2009) Global patterns of speciation and diversity. Nature 460:384–388
Etienne RS (2005) A new sampling formula for neutral biodiversity. Ecol Lett 8:253–260
Etienne RS (2007) A neutral sampling formula for multiple samples and an “exact” test of neutrality. Ecol Lett 10:608–618
Etienne RS (2009a) Improved estimation of neutral model parameters for multiple samples with different degrees of dispersal limitation. Ecology 90:847–852
Etienne RS (2009b) Maximum likelihood estimation of neutral model parameters for multiple samples with different degrees of dispersal limitation. J Theor Biol 257:510–514
Etienne RS, Alonso D (2005) A dispersal-limited sampling theory for species and alleles. Ecol Lett 8:1147–1156
Etienne RS, Alonso D (2007) Neutral community theory: how stochasticity and dispersal-limitation can explain species coexistence. J Stat Phys 128:485–510
Etienne RS, Apol MEF (2009) Estimating speciation and extinction rates from diversity data and the fossil record. Evolution 63:244–255
Etienne RS, Olff H (2005) Confronting different models of community structure to species-abundance data: a Bayesian model comparison. Ecol Lett 8:493–504
Etienne RS, Latimer AM, Silander JA, Cowling RM (2006) Comment on “Neutral ecological theory reveals isolation and rapid speciation in a biodiversity hot spot”. Science 311:610b
Etienne RS, Alonso D, McKane AJ (2007a) The zero-sum assumption in neutral biodiversity theory. J Theor Biol 248:522–536
Etienne RS, Apol MEF, Olff H, Weissing FJ (2007b) Modes of speciation and the neutral theory of biodiversity. Oikos 116:241–258
Ewens WJ (1972) The sampling theory of selectively neutral alleles. Theor Popul Biol 3:87–112
Haegeman B, Etienne RS (2008) Relaxing the zero-sum assumption in neutral biodiversity theory. J Theor Biol 252:288–294
Haegeman B, Etienne RS (2009) Neutral models with generalised speciation. Bull Math Biol 71:1507–1519
Haegeman B, Etienne RS (2010) A self-consistent approach to neutral community speciation models. Phys Rev E 81:031911
Hubbell SP (2001) The unified neutral theory of biodiversity and biogeography. Princeton University Press, Princeton
Jabot F, Chave J (2009) Inferring the parameters of the neutral theory of biodiversity using phylogenetic information and implications for tropical forests. Ecol Lett 12:239–248
Jabot F, Etienne RS, Chave J (2008) Reconciling neutral community models and environmental filtering: theory and an empirical test. Oikos 117:1308–1320
MacArthur RH (1957) On the relative abundance of bird species. Proc Natl Acad Sci U S A 43:293–295
MacArthur R (1966) Note on Mrs Pielou’s comments. Ecology 47:1074
MacArthur RH, Wilson EO (1967) Island biogeography. Princeton University Press, Princeton
McGill BJ (2003) Strong and weak tests of macroecological theory. Oikos 102:679–685
McGill BJ, Maurer BA, Weiser MD (2006) Empirical evaluation of neutral theory. Ecology 87:1411–1426
McGill B, Etienne RS, Gray JS, Alonso D, Anderson MJ, Benecha HK, Dornelas M, Enquist BJ, Green JL, He F, Hurlbert A, Magurran A, Marquet P, Maurer B, Ostling A, Soykan CU, Ugland K, White EP (2007) Species abundance distributions: moving beyond single prediction theories to integration within an ecological framework. Ecol Lett 10:995–1015
Mouillot D, Gaston K (2007) Geographical range size heritability: what do neutral models with different modes of speciation predict? Glob Ecol Biogeogr 16:367–380
Munoz F, Couteron P, Ramesh BR, Etienne RS (2007) Inferring parameters of neutral communities: from one single large to several small samples. Ecology 88:2482–2488
Nee S (2005) The neutral theory of biodiversity: do the numbers add up? Funct Ecol 19:173–176
O’Dwyer JP, Lake JK, Ostling A, Savage VM, Green JL (2009) An integrative framework for stochastic, size-structured community assembly. Proc Natl Acad Sci 106:6170–6175
Preston FW (1948) The commonness, and rarity, of species. Ecology 29:254–283
Preston FW (1962) The canonical distribution of commonness and rarity. Parts I and II. Ecology 43:185–215, 410–432
Pueyo S (2006) Diversity: between neutrality and structure. Oikos 112:392–405
Purves DW, Pacala SW (2005) Ecological drift in niche-structured communities: neutral pattern does not imply neutral process. In: Burslem D, Pinard M, Hartley S (eds) Biotic interactions in the tropics. Cambridge University Press, Cambridge, pp 107–138
Ricklefs R (1987) Community diversity: relative roles of local and regional processes. Science 235:167–171
Ricklefs RE (2003) A comment on Hubbell’s zero-sum ecological drift model. Oikos 100:185–192
Rosindell JL, Cornell SJ (2007) Species–area relationships from a spatially explicit neutral model in an infinite landscape. Ecol Lett 10:586–595
Rosindell JL, Cornell SJ (2009) Species–area curves, neutral models and long distance dispersal. Ecology 90:1743–1750
Rosindell J, Wong Y, Etienne RS (2008) A coalescence approach to spatial neutral ecology. Ecol Inform 3:259–271
Rosindell J, Cornell SJ, Hubbell SP, Etienne RS (2010) Protracted speciation revitalizes the neutral theory of biodiversity. Ecol Lett (in press)
Stanley SM (1979) Macroevolution: pattern and process. Freeman, San Francisco
Vallade M, Houchmandzadeh B (2003) Analytical solution of a neutral model of biodiversity. Phys Rev E 68:061902
Vanpeteghem D, Zemb O, Haegeman B (2008) Dynamics of neutral biodiversity. Math Biosci 212:88–98
Volkov I, Banavar JR, Hubbell SP, Maritan A (2003) Neutral theory and relative species abundance in ecology. Nature 424:1035–1037
Volkov I, Banavar JR, He F, Hubbell SP, Maritan A (2005) Density dependence explains tree species abundance and diversity in tropical forests. Nature 438:658–661
Volkov I, Banavar JR, Hubbell SP, Maritan A (2007) Patterns of relative species abundance in rainforests and coral reefs. Nature 450:45–49
Webb C, Ackerly D, McPeek M, Donoghue M (2002) Phylogenies and community ecology. Ann Rev Ecolog Syst 33:475–505
Weiher E, Keddy P (2001) Ecological assembly rules: perspectives, advances, retreats. Cambridge University Press, Cambridge
Zillio T, Condit R (2007) The impact of neutrality, niche differentiation and species input on diversity and abundance distributions. Oikos 116:931–940
Acknowledgements
We thank Franck Jabot and a few anonymous reviewers for their constructive comments. RSE thanks the financial support of The Netherlands Organization for Scientific Research (NWO).
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1: Derivation of the dynamics of \(\mathbb{E}^{\rm{meta}}(S_{n})\) and the corresponding stationary distribution
The dynamics of \(\mathbb{E}^{\rm{meta}}(S_{n})\) can be split into two parts
First, we consider the first part: dynamics due to death–birth events. The transition rate is given by
The case k = i takes into account only those events in which the dead and newborn individual belong to a different species. If not, the death–birth event has no net effect.
Species with abundance n disappear (\(S_{n}^{\prime }-S_{n}=-1\)) in transitions \(R_{k,i}^{\rm{DB}}\)
-
with k = n: an individual in a species with abundance n dies
-
with i = n: an individual in a species with abundance n reproduces
Species with abundance n appear (\(S_{n}^{\prime }-S_{n}=1\)) in transitions \(R_{k,i}^{\rm{DB}}\)
-
with k = n + 1: an individual in a species with abundance n + 1 dies,
-
with i = n − 1: an individual in a species with abundance n − 1 reproduces.
Hence,
where we defined
Note that we implicitly assumed that n > 1 and n < J M; the extension to the cases n = 1 and n = J M is straightforward.
Next, we consider the second part of Eq. 49: dynamics due to speciation events. The transition rate is given by
Species with abundance n disappear (\(S_{n}^{\prime }-S_{n}=-1\)) in transitions \(R_{k,i}^{\rm{S}}(\vec{S})\) with k = n. Species with abundance n appear (\(S_{n}^{\prime }-S_{n}=1\)) in transitions \(R_{k,i}^{\rm{DB}}( \vec{S})\) with n = i or n = k − i. Note that for k > n and k ≠ 2n, there are two fission events that lead to a new species with abundance n and that for k = 2n, there is one fission event that leads to two new species with abundance n. Hence,
where we defined
Note that we implicitly assumed that n > 1 and n < J M; the extension to the cases n = 1 and n = J M is straightforward.
Equations 56a, 56b, and 56c keep the total number of individuals in the community constant, as required:
Furthermore, the total expected species richness satisfies
where the first term describes species extinction and the second term describes speciation.
Equations 56a, 56b, and 56c are closed in \(\mathbb{E}^{\rm{meta}}( S_{n})\), that is, they do not contain expectations such as \(\mathbb{E}^{\rm{meta}}(S_{n}S_{m})\). This seems to be a general property of neutral models (Vanpeteghem et al. 2008). Similarly, we can derive the dynamical equations for the second-order moments \(\mathbb{E}^{\rm{meta}}(S_{n}S_{m})\), which are again closed, that is, they do not contain third- or higher-order moments.
The equilibrium solution of Eqs. 56a, 56b, and 56c can be found most easily by setting Eqs. 56b, 56c and 58 to zero, remembering that \(\sum\limits_{n=1}^{J_{\rm{M}}}n \mathbb{E}^{\rm{meta}}(S_{n})=J_{\rm{M}}\) and then solving for a i defined by
This yields the following expression for \(\mathbb{E}^{\rm{meta}}( S_{n})\):
with
where a 1 results from setting Eq. 58 to zero, \(a_{J_{\rm{M}}}\) from setting Eq. 56c to zero, and a i for 1 < i < J M by setting Eq. 56b to zero.
Appendix 2: Derivation of \(\mathbb{E}^{\rm{meta}}(S_{n}|J_{\rm{M}})\) from the Ansatz
\(\mathbb{E}^{\rm{meta}}(S_{n}|J_{\rm{M}})\) follows in a straightforward way from the Ansatz for \({\mathbb{P}}\):
Appendix 3: Derivation of the distribution, mean, and variance of the total number of species S M for large θ rf
We first compute the mean and variance of the number of species S M in the metacommunity for large θ rf. We have
The asymptotic behavior of the Bessel functions I α (x) is given by
where we use the big \(\mathcal{O}\) notation to describe the asymptotic behavior of a function. Hence,
so that
For the variance,
The asymptotic behavior of the distribution \({\mathbb{P}}\) for the number of species S M can be analyzed further. Taking the logarithm of Eq. 15a,
and using asymptotic formulas for the Bessel function and the factorial (Stirling’s formula),
we get
The expression in the first line, considered as a function of S M , has a maximum at θ rf. Developing this function up to second order in S M − θ rf, we get
and hence,
Thus, for large θ rf the distribution \({\mathbb{P}}\) for the number of species S M is normally distributed, with mean θ rf and standard deviation \(\sqrt{\frac{\theta _{\rm{rf}}}{2}}\).
Appendix 4: Derivation of the approximation to \(\mathbb{E}^{\rm{meta}}(S_{n}|J_{\rm{M }})\) and \(\mathbb{E}^{\rm{meta}}(S_{k}S_{\ell }|J_{\rm{M}})\)
We start by computing the expectations of the number of species with abundance n in the metacommunity and of S k S ℓ conditional on metacommunity size J M and total number of species S M. First, consider the trivial case that S M = 1. The abundance of the only species present is equal to the metacommunity size. Hence,
Next, consider the case that S M ≥ 2. We have
Assuming that J M is large we find
Similarly, one can compute the expectation of higher-order moments of S n . We illustrate this for the expectation \(\mathbb{E}^{\rm{meta} }(S_{k}S_{\ell }|J_{\rm{M}},S_{\rm{M}})\) with k ≠ ℓ. First, consider the case with S M = 2. The abundances of the two species present should sum up to the metacommunity size, k + ℓ = J M. Hence,
Next, consider the case with S M ≥ 3. We have
Assuming that J M is large leads to
Now we are ready to compute the same quantities without conditioning on S M. The number of species with J M individuals, \(S_{J_{ \rm{M}}}\), is different from zero only if there is a single species in the community. The expected number of species \(\mathbb{E}(S_{J_{\rm{M}}}|J_{ \rm{M}})\) is therefore equal to the probability that there is only one species in the community, \(P(S_{\rm{M}}=1)=\frac{\theta _{\rm{rf}}}{ I_{1}\left( 2\theta _{\rm{rf}}\right) }\). To compute the expectation \( \mathbb{E}(S_{n}|J_{\rm{M}})\) for n < J M, we only have to consider communities with at least two species. Assuming that J M is large, we have
The product S k S ℓ with k + ℓ = J M is different from zero only for communities with two species, one with abundance k and the other with abundance ℓ. Hence, the expectation \(\mathbb{E} (S_{k}S_{\ell }|J_{\rm{M}})\) with k + ℓ = J M has only contributions from two-species communities. To compute the expectation \( \mathbb{E}(S_{k}S_{\ell }|J_{\rm{M}})\) with k + ℓ < J M, we only have to consider communities with at least three species. Assuming that J M is large, we have
Appendix 5: Derivation of the sampling formula \({\mathbb{P}}\)
The derivation starts with the general formula for a dispersal-limited sample (Etienne and Alonso 2005) where we make the conditioning on S M explicit:
By multiplying with \({\mathbb{P}}\) and summing over all S M, we find
We can now substitute Eq. 18c and use the Stirling number formulation of the Pochhammer symbol, Eq. 34,
with A = ∑ i a i . Next we evaluate the integral,
because a i = 0 for all species that are not present in the sample. Substituting this and Eq. 12, we obtain
The sum over S M can be expressed in terms of the modified Bessel function of the first kind,
Substituting this and Eq. 15b in Eq. 84, we obtain our final result (Eq. 33):
This formula can be evaluated numerically, similarly to the sampling formula for the point mutation model (Etienne 2005). If there is no dispersal limitation (i.e., let I→ ∞), we have
where in the third line we have used Eq. 85.
Appendix 6: Derivation of \(\mathbb{E}^{\rm{smp}}(S_{n}|I,\theta _{\rm{rf}},J)\)
We derive \(\mathbb{E}^{\rm{smp}}(S_{n}|I,\theta _{\rm{rf}},J)\) (for n < J ) by following Alonso and McKane (2004) and Etienne and Alonso (2005). We take a dispersal-limited sample from the metacommunity where the density of species with relative abundance p in the metacommunity with S M species is given by \(S_{\rm{M}}\rho ^{\rm{meta}}(p|S_{\rm{M}})\):
We can also retain the integral (instead of writing it in terms of Stirling numbers) and write
Alternatively, we can directly use our sampling formula to obtain
All these expressions can be shown to be mathematically identical.
If there is no dispersal limitation, these equations can be simplified. Equation 88 reduces to
where 1 F 2(a,{b,c},x) is the generalized hypergeometric function.
Likewise, Eq. 89 reduces to
and Eq. 90 reduces to
Appendix 7: The fundamental biodiversity number θ
We treated the death–birth process and the speciation process as decoupled processes. The point mutation mode of speciation, however, was originally envisioned as a birth event where a crucial mutation had caused a new species to arise, and therefore, speciation and birth are related to one another. If the death–birth rate is \(\widetilde{\mu }\) and the probability of a birth resulting in an individual of a new species is \(\widetilde{\nu }_{ \rm{pm}}\), then the transition rates for the point mutation model can be written as:
and
These transition rates are identical to the ones in Eqs. 3 and 6 if we set
Hence, we observe that a simple transformation of the parameters makes the equations identical.
The fundamental biodiversity number θ is defined in the point mutation model as the number of speciation events per birth event, or the ratio of the speciation rate and the per capita birth rate. Because the per capita birth rate is the overall death–birth rate divided by the total number of individuals after a death event, J M − 1, we have for the model where the processes of speciation and death–birth are decoupled, the following formula for θ pm
while in the model where they are related, θ pm is expressed as
With Eq. 96, we see that these formulas coincide.
In the random fission model, we defined the fundamental biodiversity number in a different way: We used the appropriate scaling of ν and J M in the limit of J M→ ∞, ν rf →0 which is in this case such that \(\theta _{\rm{rf}}=\sqrt{ \nu _{\rm{rf}}}J_{\rm{M}}\) is finite. In the point mutation model, we could also have defined θ pm by the appropriate scaling which is in this case such that θ pm = ν pm J M Hence, for point mutation, the scaling definition practically coincides with the definition as the number of speciation events per birth event, but for random fission, these definitions are different. We chose this scaling definition because with this definition the species abundance distribution behaves similarly (Fig. 3).
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License (https://creativecommons.org/licenses/by-nc/2.0), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Etienne, R.S., Haegeman, B. The neutral theory of biodiversity with random fission speciation. Theor Ecol 4, 87–109 (2011). https://doi.org/10.1007/s12080-010-0076-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12080-010-0076-y