Abstract
Introduction
The Sniffin’ Sticks threshold test is widely used to assess olfactory threshold due to its high reliability and validity. Nevertheless, this test procedure is quite long with an average duration of 10 to 20 min. In study designs that require multiple olfactory threshold tests on short intervals, this could exhaust participants. To counteract this limitation, we developed the informed-four-reversal (INFOUR) short version of the Sniffin’ Sticks threshold test for repeated measurement designs and piloted it in a sample of normosmic participants.
Methods
Forty-two participants performed the original Sniffin’ Sticks version before being assigned either to the control group that repeated the original version or to the test group that conducted the INFOUR short version.
Results
The correlation between the original version at T1 and INFOUR at T2 was r = .75 and did not differ significantly from the retest reliability of the original version. Compared to the original version, the INFOUR took 42% less time to perform.
Conclusion
The INFOUR leads to a significant time saving, while maintaining good validity.
Implications
Therefore, this approach has the potential to be a useful tool for study protocols with repeated olfactory threshold measurements. In particular, when research protocols are time intensive or testing needs to the shortened, because the interventional effects are short or subtle.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Smelling often plays part in experimental settings, e.g., after emotion induction (Chan et al. 2020; Flohr et al. 2017; Pollatos et al. 2007) or stress induction (Pacharra et al. 2016). For such designs, it is important to assess olfactory performance as precisely as possible. Varieties of methods have been used for this assessment. The University of Pennsylvania Smell Identification Test (UPSIT) is the most widely used olfaction test in North America (Doty et al. 1995), whereas the TT olfactometer is frequently used in Japan (Kondo et al. 1998). Another tool often used in Europe is the Sniffin’ Sticks test, which allows differentiated testing of olfactory identification, discrimination, and threshold (Hummel et al. 1997). This test has been validated in hyposmic and anosmic patients with normative data collected in over 9000 individuals (Oleszkiewicz et al. 2019). The test–retest reliability of this instrument is r = 0.61–0.84, when tests are several days apart (Croy et al. 2009; Hummel et al. 1997). However, a much weaker test–retest reliability of r = 0.31 was observed in another study, what indicates fluctuations of threshold measurement (Oleszkiewicz et al. 2017).
The original threshold test of the Sniffin’ Stick battery is performed as follows (Fig. 1a): The participant is asked to close eyes to avoid visual distraction. A group of three pens (triplet) is consecutively presented beneath the participant’s nostrils with approximately 20 s between triplets to avoid adaptation. The triplet consists of one odorized target pen and two blanks. The participant is asked to detect the odorized target in an alternative forced-choice paradigm. The whole test battery consists of 16 triplets, representing different concentrations of the target with a higher triplet number indicating lower concentration. The triplets are presented in a single-staircase method (Ehrenstein and Ehrenstein 1999): The first triplets are given in ascending order, starting at the lowest concentration until the participant correctly detects the target twice in a row. This correct detection triggers a reversal of triplet presentation—towards lower concentrations—until odor detection fails (1 up 2 down stopping rule). The procedure stops when seven reversals are obtained. The mean score of the last four reversal points represents the participant’s odor threshold.
Example of the testing protocol for a) the original Sniffin’ Stick threshold assessment, b) the ascending limits procedure (ALP, Sijben et al. 2017), c) the brief ascending procedure (BAP, Pössel et al. 2020), and d) the wide steps method (WSM, Croy et al. 2009). An X indicates a correct detected target pen in a triplet, a minus indicates an incorrect detected target pen; arrows pointing up and down refer to steps in higher or lower directions; red dashed circles mark the trials that are included in the score calculation
However, the test procedure for assessing the olfactory threshold is relatively long, lasting 10 to 20 min (Besser et al. 2019; Hummel et al. 1997). This length is problematic in study designs where the threshold needs to be measured repeatedly or where participants are vulnerable to exhaustion, like patients with mental disorders. In these cases, the relatively long procedure can lead to fatigue, diminished attention or frustration, and therefore bias olfactory test results.
In order to tackle this issue, shorter versions of the olfactory threshold test have already been developed. One shortened approach is the ascending limits procedure (Sijben et al. 2017, compare Fig. 1b). Similar to the original procedure, this shortened version starts with the triplet containing the lowest concentration, and the concentration is increased after every incorrect answer. Unlike the original version, this ascending procedure stops after the participant correctly detects the odor in four consecutive triplets. This leads to an average time reduction of around 30% compared to the original method. The outcome of the ascending limits procedure correlates to the original threshold test with r = 0.59.
Using a small sample of n = 20 young subjects Pössel and colleagues (2020) developed a brief ascending procedure (compare Fig. 1c), which is comparable to the ascending limits procedures, but each triplet is only presented once. The procedure stops when five triplets in a row are successfully detected, resulting in a very conservative approach, which biases subjects towards detecting relatively higher concentrations. This results in a promising time reduction of 51% with a correlation of r = 0.76 to original Sniffin’ Sticks threshold test and retest-reliability of r = 0.68 within one week. Additionally, Pössel et al. (2020) simulated another shortened threshold score test. The authors performed the original Sniffin’ Sticks threshold test with seven reversals, but calculated the score by the last two out of the previous five reversals. Therefore, this procedure correlated high with the original procedure r = 0.98 and was 26% shorter in duration.
Another approach is the wide steps method (Croy et al. 2009, compare Fig. 1d). In contrast to the original version, only eight concentrations (every second concentration from the original version) are presented to the participants. This procedure leads to a time reduction of 18% with a retest reliability of r = 0.84. The correlation to the original Sniffin’ Sticks version is r = 0.88.
Although all shortened versions show benefits in duration and good reliability, these brief olfactory threshold tests are limited due to a poorer resolution compared to the original version. Therefore, the use of such brief procedures is recommended when larger group differences are expected (Pössel et al. 2020). This is a potential disadvantage for repeated measurement designs if only subtle effects are of interest. Another approach worth mentioning is the method of constant stimuli, where triplets of all levels of concentration are presented only once and in randomized order (Lötsch et al. 2004). Threshold scores are obtained by logistic regression, according to the assumption that the probability of correct detection is high, when the odor is actually perceived compared to a chance level probability when the odor is not perceived. While the advantage of this procedure is that the number of triplets remains constant, it yet again is limited in its resolution, as subjects are either extremely sensitive (scoring very high) or insensitive (scoring very low).
We therefore aimed to develop another short version of the Sniffin’ Sticks threshold test, which can be used in consecutive olfactory threshold measurements. This procedure utilizes an informed four-reversal-threshold approach (INFOUR). The INFOUR starts with determination of the olfactory threshold score by conducting the original version. This threshold forms the starting point of the INFOUR (first concentration presented), which is set to the original threshold result minus three concentration steps (Fig. 2). This conservatively chosen informed starting point allows a time-efficient approach to the expected threshold value, and at the same time prevents a possible underestimation of the resulting threshold value. With this starting point, the INFOUR is in principal performed like the original Sniffin’ Sticks threshold, but only with four instead of seven reversal points. The final test score is then calculated out of the last three reversal points by summing up all correctly detected targets. After the odor is detected twice in a row, the sum of all subsequent triplets containing higher odor concentration is multiplied by two and added to the result. The first reversal score is not included in the calculation to allow some time for adaptation.
Example of a testing protocol according to the INFOUR procedure, while a) T1 corresponds to the original Sniffin’ Sticks assessment, the score from this test is used to calculate the start point (gray shaded) for b) the shortened INFOUR at T2. All correct detected targets are counted, with the assumption that if the odor is detected twice in a row, the participants can detect all subsequent dilutions of higher odor concentrations. For this, only the last three reversals of the original version and of the INFOUR are used, instead of the last four reversals of the original version and all INFOUR reversals. According to this, three reversals with 16 dilutions, where each dilution is detected correctly twice, result in a sum score of 96, which equals a 100% threshold; red dashed circles mark the trials that are included in the score calculation
We hypothesized that the olfactory threshold measured by the INFOUR shows high validity, operationalized by the correlation to the original version (H1). We further hypothesized that the INFOUR requires less time than the original version (H2). As a good testing procedure should not have interventional aspects, we tested whether the INFOUR impairs mood (H3).
Materials and Methods
Participants
Forty-two participants (28 females) aged 20.8–68.4 years (mean = 30.7 years ± 11.7 years SD) took part in the study. Exclusion criteria were self-reported olfactory impairments and self-reported health impairments that are associated with disorders of olfactory function (e.g., sinonasal disorders, Parkinson’s disease, renal insufficiency).
Participants were instructed not to eat, smoke or drink anything other than water 1 h prior to testing. Participants were pseudo-randomized into two equal groups based on sex and age similarity, as age and sex can affect performance in the Sniffin’ Sticks test (Hummel et al. 2007).
The ethics committee of the University of Dresden approved the conduction of the study (EK 229062018), which is in accordance with the “World Medical Association’s Declaration of Helsinki”. Written informed consent was obtain from all participants.
Sample Size Estimation
To a priori determine the minimum number of participants required, we used G*Power software (Faul et al. 2007). Informed by previous results (Croy et al. 2009; Pössel et al. 2020), we set the expected correlations of the original threshold with our INFOUR procedure to r = 0.70, which is considered as large effect size according to the classification of Cohen (1988). The optimal sample size to statistically ensure a high effect with α = 0.05 and 1-β = 0.80 is calculated to n = 11 participants. For group comparisons at T1 and T2 with α = 0.05 and 1-β = 0.80, a total number of n = 42 participants needs to be tested, to statistically ensure differences of high effect sizes (d = 0.80).
Testing Procedure
In a repeated measurements between-subject design, participants were tested twice for olfactory function. Both tests were separated by a short break in which participants filled out the Positive and Negative Affect Schedule (PANAS; Watson et al. 1988). This reliable and valid 20-item self-report measure assesses positive and negative affect on two scales. In the PANAS, respondents rate the extent to which they have experienced a certain mood within a specified period, based on a 5-point scale (from 1 “not at all” to 5 “extremely”). In our experiment, we asked participants to “rank how you feel right now”. In a non-clinical sample (N = 1003) the mean score for positive affect (PA) is 31.31 (SD = 7.65) and for negative affect (NA) 16.00 (SD = 5.9) (Crawford and Henry 2004).
After reading the study information, all participants performed the original version of the Sniffin’ Sticks threshold test (Hummel et al. 1997) as explained in the introduction. In each triplet of the Sniffin’ Sticks markers, one stick is filled with the odorant target (phenyl ethyl alcohol in aqua conservans) while the others contain aqua conservans only. Pens are color-coded to enable the experimenter to distinguish between target pen and blanks. The pen with the highest concentration contains 4% of the odorant and subsequent levels are diluted by a ratio from 1:2 in a geometric series. The pen was held approximately 2 cm in front and beneath the nostrils. In deviation from the original testing protocol, participants were instructed to leave their eyes open and focus the wall in front of them. We chose this modification to make the test design more flexible for variable testing environments, for example for experiments with simultaneous olfactory and visual stimulation. The experimenter sat directly beside the participant to avoid possible hints by the experimenter’s facial expressions. A box covered the testing battery to ensure that the color codes on the sticks were not visible to the participant.
For the second trial, one group repeated the original version (group 1) again while the other received the INFOUR version as outlined in the introduction (group 2). The break in between was set to 15 min, which was in line with (Sijben et al. 2017) or even longer than previous related study designs (Besser et al. 2019; Pössel et al. 2020).
For all threshold tests, we recorded the duration via stopwatch and counted all the triplets required to reach the threshold. Immediately after the second olfactory threshold test, participants filled out the PANAS a second time. At the end of the experiment, we debriefed all participants and provided feedback on their olfactory threshold.
Statistical Analysis
We calculated threshold percentage scores of the last three reversals as previously described. Therefore, our threshold equals a ratio of all correctly detected target pens to all potential targets, which ensures a higher resolution of the INFOUR score than an average score of the last three reversals. To keep data comparable, we used this calculation for all threshold scores (original version at T1 and T2 and INFOUR at T2).
We excluded one male participant, who was originally assigned to group 2 from analysis, because his olfactory score with a value of one was identified as outlier via box plot test. This strongly deviating score would lead to an overestimation of the correlation between T1 and T2 for threshold scores.
We used the IBM SPSS Statistics software version 25 (IBM Corp Released 2017) for all data analysis, except for Bayesian statistics, which were performed using the open-source statistic package JASP (JASP Team 2019).
In order to test hypothesis 1, we compared the outcome of the original Sniffin’ Sticks between groups at T1 and we compared the outcome of the original Sniffin’ Sticks and the INFOUR at T2 via T tests for independent samples. In the next step, we analyzed the relationship between thresholds at T1 and T2 for each group using Pearson’s product-moment correlations. In alignment with the method described by Eid et al. (2013) we calculated whether the correlation coefficients between both groups differed significantly.
Additionally, we ran both analyses with the Bayesian statistics approach. The advantage in Bayesian statistics is the ability to test the considered likelihood of an outcome through a null and alternative hypothesis, while common statistics only allows testing the null hypothesis. Bayes factor (BF) of > 1 reflects evidence for the null hypothesis and values < 1 for the alternative hypothesis. The classification scheme of Lee and Wagenmakers (2014) was used to interpret the BF with descriptive labels. Based on prior specification for Bayesian analytics, we used the default Cauchy distribution of r = 0.707 (Jeffreys 1961), which is recommended if parameters are unconstrained because it is similar to the normal distribution but has less central mass by wider tails (Quintana and Williams 2018).
In order to test hypothesis 2, we performed group comparisons at T1 and T2 for the minutes and triplets needed to perform the procedures. Non-parametric tests for independent samples were chosen as the Shapiro–Wilk test indicated violations of the assumption of normal distribution. Additionally, we run both analyses with the Bayesian statistics approach as outlined above.
In order to test hypothesis 3, we performed a two-way (“Procedure”) × 2 (“Time”) repeated measures analysis of variance (rm-ANOVA) for measurement of mood impairments. As the negative subscale of the PANAS was not normally distributed, we additionally controlled our results with non-parametric tests, and we reached the same result in principle. Because of the relative robustness of the rm-ANOVA against deviations of assumptions of normal distribution, we report the rm-ANOVA results. Additionally, we ran a Bayesian rm-ANOVA for positive and negative affect scores separately to report outcomes under null and alternative hypothesis.
Results
Threshold
Mean threshold scores are presented in Table 1 and Fig. 3. In addition, all reversal points for each individual are presented in Fig. 4. Visual inspection of this figure shows that there are no major adaptation or sensitization effects, but the threshold remains fairly stable. Threshold of groups differed neither significantly at T1 (t(39) = − 1.076, p = 0.289, d = − 0.366), where both groups performed the original version, nor at T2 (t(39) = − 1.032, p = 0.309, d = − 0.322), where one group performed the INFOUR. A Bayes factor of BF01 = 2.064 at T1 indicates that the data is 2.1 times more likely to occur under the null hypothesis (no group differences) than under the alternative hypothesis. Group comparison at T2 revealed a Bayes factor of BF01 = 2.141, again indicating that the data is also 2.1 times more likely to occur under the null than under the alternative hypothesis.
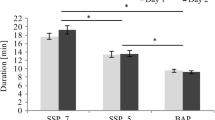
a) Correlation of olfactory threshold of T1 and T2, separated by groups (yellow for the group 1, which repeated the original Sniffin’ Sticks threshold test a second time and green for group 2, which performed the INFOUR at T2). b) Threshold and c) duration in minutes and in triplets at T1 and T2, error bars indicate standard deviations. Note that both groups (original vs. INFOUR) performed the original version at T1
Olfactory thresholds at T1 and T2 correlated with r = 0.74 (p < 0.001) in group 1 and with r = 0.75 (p < 0.001) in group 2 (Fig. 3a). The Bayesian Pearson Correlation showed extreme evidence in favor of the alternative hypothesis (outcomes at T1 and T2 are correlated) for both groups (original version at T2: BF01 = 0.004, INFOUR at T2: BF01 = 0.005). The correlation coefficients did not differ significantly between both groups (z = − 0.04, p = 0.484).
Duration
At T1, when the test procedure was the same for both groups (compare Table 1 and Fig. 3c), we found neither a robust group difference for the test time (z = − 0.835, p = 0.404, BF01 = 2.866) nor for the number of triplets (z = − 0.616, p = 0.616, BF01 = 3.034). At T2, the INFOUR group was on average 4 min 53 s faster and required 10 fewer triplets than the other group (see Table 1, Fig. 3b). This represents a time reduction of 42%. Statistical testing indicates that this group difference at T2 is substantial for both test time (z = − 4.565, p < 0.000, BF01 = 0.009) and number of triplets (z = − 4.947, p < 0.000, BF01 = 0.004). Both Bayes factors provide high evidence in favor of the alternative hypothesis over the null hypothesis.
Mood
We found a significant difference in mood across testing, but only for negative mood (main effect “Time”: df = 1; F = 14.25, p < 0.001) indicating that negative mood diminished during the experiment independent of group assignment. All other effects on negative mood (main effect “Procedure” and interaction effect) were non-significant. Bayesian rm-ANOVA showed very strong evidence in favor of the main effect “Time” (BF01 = 0.019). Comparison of the null hypothesis with the main effect “Procedure”, reveals anecdotal evidence for null hypothesis (BF01 = 1.561).
There was neither a significant main nor interaction effect for positive mood. Bayesian rm-ANOVA showed for positive affect, there is moderate evidence in favor of the null hypothesis versus the interaction “Time” × “Procedure” (BF01 = 4.219), anecdotal evidence, that the null hypothesis is more favored than main effect “Time” (BF01 = 2.510), and anecdotal evidence in favor of the null hypothesis versus the main effect “Procedure” (BF01 = 1.802). Mean PANAS scores are presented in Table 1 and Fig. 5.
Discussion
The aim of the study was to develop a short version of the Sniffin’ Sticks threshold test, which has a better resolution than previously proposed short versions, and a high validity, but takes significantly less time than the original version. Based on our results, the INFOUR seems to fulfill these requirements. The olfactory threshold obtained in the original version was highly correlated to the threshold obtained by the INFOUR procedure, indicating that the INFOUR is a valid measurement of olfactory threshold. According to this, the alignment of thresholds between short and original version did not differ significantly from the retest reliability of the original version. It should be noted that the reliability of the original version in our study falls slightly behind previous results of comparable intervals between two tests, with r = 0.74. Indeed, the original Sniffin’ Sticks threshold has shown satisfying retest reliabilities between r = 0.82–0.85 in healthy participants, when the test is repeated several minutes later (Albrecht et al. 2008). However, when the test was assessed on different days, reliability is more dispersed between r = 0.31–0.85 (Croy et al. 2009; Hummel et al. 1997; Oleszkiewicz et al. 2017), indicating that there are individual fluctuations in olfactory ability across days.
Additionally, we modified the calculation of the threshold score. We used only the last three instead of the last four reversals. We did this because the first reversal of the INFOUR is based on the informed starting point (original threshold result minus three concentration steps). Including this reversal into calculation would increase the risk for false negative results and lead to threshold overestimation.
The calculation of the olfactory threshold out of only three reversal steps comes at costs. First, this approach leaves only one step for adaptation, making the INFOUR also potentially prone to threshold overestimation. However, our data suggests that this is not a major issue and we found no indication for a need of longer adaptation. However, the INFOUR is not conceived as a standalone threshold measurement but rather as a continuation of threshold assessment in repeated measurement. Thus, performing the INFOUR after a complete original Sniffin’ Sticks threshold test could shorten the time it takes to get used to the procedure or the smell and at the same time, this method makes advantage of the warm-up effect (O’Mahony et al. 1988) – at least for designs where measurements are performed within one day.
Second, the reduced number of reversal steps can lead to a higher rate of false positive results and this limitation should be considered in the decision of whether one uses the INFOUR for repeated measurement designs or the full Sniffin’ Sticks threshold test. Still, false positive rates are influenced by the number of presentations (Running 2015).
To not diminish resolution by dividing sum scores by three instead of four, we used percentage scores in contrast to the original average threshold score. To keep results comparable, we calculated threshold scores along this approach for the original version (at T1 and T2) as well as for the INFOUR. We tested for correlations with non-modified threshold scores and found highly satisfying correlations of r = 0.93–0.99 for the original version at T1 and T2 and r = 0.99 for the INFOUR at T2.
The main advantage of the INFOUR is its significant time saving. This is achieved by the beginning at an informed starting point – which is especially pronounced in individuals with lower sensitivity – as well as a shortened number of reversals. The INFOUR took 42% (approximately 5 min or 10 triplets) less time than the repeated performance of the original version. This is practically relevant and exceeds the time improvement obtained by the ascending limits procedure (Sijben et al. 2017) and the wide steps method (Croy et al. 2009). Therefore, the INFOUR is a useful tool in certain fields of application, but requires further validation for other purposes such as longer time intervals between testing.
We conclude that the shortened version is suited for experimental designs where olfactory threshold is assessed multiple times, such as intervention studies or provocation designs (e.g., effects of mood or stress induction on olfaction). Furthermore, we are confident that the INFOUR can be used for studies with a longer time scale, e.g., for studying potential differences of olfactory perception related to menstruation cycle or before versus after nasal surgeries, but further tests for reliability are recommended. However, it should be noted that our results are derived from a normosmic sample.
Nevertheless, the strength of the INFOUR is that testing procedure is faster than the repetition of the original version while maintaining good validity. This provides great advantage in testing procedures where research protocols are time intensive, or if the effect of an intervention (e.g., mood induction) is short and hence tests need to provide more immediate results. The longer a test lasts, the more likely it is that compliance will decrease, and the test subjects will become tired, bored, or exhausted. Although we did not find a significant effect on mood, we suspect benefits for multiple measurements with the INFOUR.
Change history
22 February 2022
The original version of this paper was updated to add the missing compact agreement Open Access funding note.
References
Albrecht J, Anzinger A, Kopietz R, Schopf V, Kleemann AM, Pollatos O, Wiesmann M (2008) Test-retest reliability of the olfactory detection threshold test of the Sniffin’ sticks. Chem Senses 33:461–467. https://doi.org/10.1093/chemse/bjn013
Besser G, Liu DT, Renner B, Mueller CA (2019) Self-Administered Testing of Odor Threshold and Discrimination Using Sniffin’ Sticks—Reviving the “Odor-Curves-On-Paper” Method Chemosens Percept. https://doi.org/10.1007/s12078-019-09263-x
Chan KQ, van Dooren R, Holland RW, van Knippenberg A (2020) Disgust lowers olfactory threshold: a test of the underlying mechanism. Cogn Emot 34(3):621–627. https://doi.org/10.1080/02699931.2019.1660145
Cohen J (1988) Statistical Power Analysis for the Behavioral Sciences, 2nd edn. Lawrence Erlbaum Associates Publishers, Hillsdale
Crawford JR, Henry JD (2004) The Positive and Negative Affect Schedule (PANAS): Construct validity, measurement properties and normative data in a large non-clinical sample. Br J Clin Psychol 43:245–265. https://doi.org/10.1348/0144665031752934
Croy I, Lange K, Krone F, Negoias S, Seo HS, Hummel T (2009) Comparison between odor thresholds for phenyl ethyl alcohol and butanol. Chem Senses 34:523–527. https://doi.org/10.1093/chemse/bjp029
Doty RL, McKeown DA, Lee WW, Shaman P (1995) A Study of the Test-retest Reliability of Ten Olfactory Tests. Chem Senses 20(6):645–656. https://doi.org/10.1093/chemse/20.6.645
Ehrenstein WH, Ehrenstein A (1999) Psychophysical Methods. In: Windhorst U, Johansson H (eds) Modern Techniques in Neuroscience Research. Springer, Berlin, pp 1211–1241
Eid M, Gollwitzer M, Schmitt M (2013) Statistik und Forschungsmethoden. Beltz, Weinheim (Germany)
Faul F, Erdfelder E, Lang A-G, Buchner A (2007) G* Power 3: A flexible statistical power analysis program for the social, behavioral, and biomedical sciences. Behav Res Methods 39:175–191
Flohr EL, Erwin E, Croy I, Hummel T (2017) Sad Man’s Nose: Emotion Induction and Olfactory Perception. Emotion 17(2):369–378. https://doi.org/10.1037/emo0000224
Hummel T, Sekinger B, Wolf SR, Pauli E, Kobal G (1997) ‘Sniffin’ Sticks’: Olfactory Performance Assessed by the Combined Testing of Odor Identification, Odor Discrimination and Olfactory Threshold. Chem Senses 22(1):39–52. https://doi.org/10.1093/chemse/22.1.39
Hummel T, Kobal G, Gudziol H, Mackay-Sim A (2007) Normative data for the “Sniffin’’ Sticks" including tests of odor identification, odor discrimination, and olfactory thresholds: an upgrade based on a group of more than 3,000 subjects.” Eur Arch Otorhinolaryngol 264:237–243. https://doi.org/10.1007/s00405-006-0173-0
IBM Corp (Released 2017) IBM SPSS Statistics for Windows, Version 25.0 [Computer software]. IBM Corp, Armonk, NY
JASP Team (2019) JASP (Version 0.11.1)[Computer software]
Jeffreys H (1961) The theory of probability. Oxford University Press, Oxford
Kondo H, Matsuda T, Hashiba M, Baba S (1998) A study of the relationship between the T&T olfactometer and the University of Pennsylvania Smell Identification Test in a Japanese population. Am J Rhinol 12(5):353–358
Lee MD, Wagenmakers E-J (2014) Bayesian cognitive modeling: A practical course. Cambridge University Press, Cambridge
Lötsch J, Lange C, Hummel T (2004) A simple and reliable method for clinical assessment of odor thresholds. Chem Senses 29(4):311–317. https://doi.org/10.1093/chemse/bjh034
Oleszkiewicz A, Pellegrino R, Pusch K, Margot C, Hummel T (2017) Chemical complexity of odors increases reliability of olfactory threshold testing. Sci Rep 7:39977. https://doi.org/10.1038/srep39977
Oleszkiewicz A, Schriever VA, Croy I, Hähner A, Hummel T (2019) Updated Sniffin’Sticks normative data based on an extended sample of 9139 subjects. Eur Arch Otorhinolaryngol 276(3):719–728
O’Mahony M, Thieme U, Goldstein LR (1988) The Warm-up Effect as a Means of Increasing the Discriminability of Sensory Difference Tests. J Food Sci 53:1848–1850. https://doi.org/10.1111/j.1365-2621.1988.tb07858.x
Pacharra M, Schaper M, Kleinbeck S, Blaszkewicz M, Wolf OT, van Thriel C (2016) Stress lowers the detection threshold for foul-smelling 2-mercaptoethanol. Stress 19(1):18–27. https://doi.org/10.3109/10253890.2015.1105212
Pollatos O et al (2007) Emotional stimulation alters olfactory sensitivity and odor judgment. Chem Senses 32(6):583–589. https://doi.org/10.1093/chemse/bjm027
Pössel M, Freiherr J, Horstmann A (2020) Rapid Assessment of Olfactory Sensitivity Using the “Sniffin’ Sticks”. Chemosens Percept 13:37–44. https://doi.org/10.1007/s12078-019-09261-z
Quintana DS, Williams DR (2018) Bayesian alternatives for common null-hypothesis significance tests in psychiatry: a non-technical guide using JASP. BMC Psychiatry 18(1):178. https://doi.org/10.1186/s12888-018-1761-4
Running CA (2015) High false positive rates in common sensory threshold tests. Atten Percept Psychophys 77:692–700. https://doi.org/10.3758/s13414-014-0798-9
Sijben R, Panzram C, Rodriguez-Raecke R, Haarmeier T, Freiherr J (2017) Fast Olfactory Threshold Determination Using an Ascending Limits Procedure. Chemosens Percept 11(1):35–41. https://doi.org/10.1007/s12078-017-9239-1
Watson D, Clark LA, Tellegen A (1988) Development and validation of brief measures of positive and negative affect: the PANAS scales. J Pers Soc Psychol 54(6):1063–1070
Acknowledgements
The work by Sarah Beutler was supported by Fellowship of the Heinrich Böll Foundation. Liliana R. Ladner was supported by the Deutscher Akademischer Austauschdienst (DAAD) Research Internships in Science and Engineering Program. We express our gratitude to these funders.
Funding
This research was funded by the German Research Foundation (Deutsche Forschungsgemeinschaft, DFG), Grant number: CR 479/9–1 (http://www.dfg.de/). Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Ethical Approval
All procedures performed in studies involving human participants were in accordance with the ethical standards of the institutional and/or national research committee and with the “World Medical Association’s Declaration of Helsinki”. It was approved by the ethics committee of the University of Dresden (Approval No. EK 229062018).
Informed Consent
Informed consent was obtained from all individual participants included in the study, where they all gave their written consent.
Conflict of Interest
The authors declare no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Beutler, S., Ladner, L.R., Hummel, T. et al. A New Method for a Shorter and Valid Assessment of Olfactory Threshold in Repeated Measurement Designs Based on the Sniffin’ Sticks Test. Chem. Percept. 15, 26–34 (2022). https://doi.org/10.1007/s12078-021-09291-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12078-021-09291-6