1 Introduction

Research activities on business failure are carried out with the main purpose of enhancing methods and models for understanding and predicting firms’ financial crisis. In the literature, a great attention has been devoted to the analysis of the determinants of firms’ default, especially during recent business turmoil. Both empirically and theoretically, it has been analysed the impact of macroeconomic risk components and individual characteristics on firms’ likelihoods of defaulting (Box et al. 2020).

Since (Altman 1983), a broad literature has arisen which deals with the relationship between macroeconomic variables and bankruptcy rate, both in a cross-sectional and time series context. Notably, many scholars have investigated the impact of business cycle on aggregate default rate (Hol 2007; Hudson 1986; Ilmakunnas and Topi 1999; Jacobson et al. 2013; Levy and Bar-niv 2011). Other authors have focused on other macroeconomic indicators like inflation, exchange rates, unemployment, wage or interest rate (see Dewaelheyns and Van Hulle 2007). Another interesting field is related to the impact of institutional factors, like legal or policy reform, on bankruptcy rates (Detotto et al. 2019; Dewaelheyns and Van Hulle 2008; Liu 2002; Turner et al. 1992). More recently, the role of geography in explaining cross-region patterns of bankruptcy rate is also investigated (Buehler et al. 2012).

Another strand of research has focused on the importance of the propagation of bankruptcy across economic agents. A number of studies have documented spillover effects of bankruptcy events where a firm’s financial failure is transmitted to its rivals, suppliers, or creditors (Ferris et al. 1997; Helwege and Zhang 2016; Hertzel et al. 2008; Jorion and Zhang 2007, 2009; Kolay et al. 2015; Lang and Stulz 1992). In this framework, it is well known that geographical proximity is an important element for linkages between agents, like households, firms or banks, since one is more likely to interact with other agents nearby. Few studies provided evidences of the contagions effect of distress events on local firms (Addoum et al. 2020; Benmelech and Bergman 2011; Brunnermeier and Pedersen 2009; Dick and Lehenert 2010; Kaminsky et al. 2003; Vayanos 2004).

This paper aims to study the spatial and intersectoral spill-overs in aggregate failure rates using the Spanish regions as case-study in the time span 2005Q1-2013Q4. More precisely, the purpose of this paper is twofold. First, we study the neighbouring effects on regional bankruptcy rate by employing a spatio-temporal model which allow us to analyse both spatial and temporal variability. Thus, our goal is to check for the presence of spatial spillover effects of business failure in Spanish regions for 2005 to 2013. The positive spatial spillover effects resulting from business default rate have been demonstrated by many empirical studies, which show that the likelihood of defaults in one area affects the likelihood in another neighbouring area (Addoum et al. 2020; Grana 2019; Laudenbach et al. 2021; Niessen-Ruenzi et al. 2020; Pesaranet al. 2005; Vayanos 2004). Second, the paper investigates the presence of spillovers across sectors, focusing on the relationship between bankruptcies in Agriculture, Industry and Services. The rationale comes from the dependence across firms belonging from different industries and/or sectors. So, a“contagious”propagation of business failure can be observed from one sector to the others. The analysis of bankruptcy spill-over effects is a recent strand of research (Benmelech and Bergman 2011; Kaminsky et al. 2003; Jorge and Rocha 2020; Le and Ngo 2020; Nguyen 2019). This paper tries to contribute to this discussion by looking at potential spill-over effects across three economic sectors, namely Agriculture, Industry and Services.

Spain makes an interesting case study because it represents the eurozone’s fourth-largest economy and, during the period analysed, it experienced a tremendous economic crisis. For example, Spain passed from 919 bankruptcy cases in 2005 to 9022 in 2013 which means a dramatic increase by 881.7\(\%\) (calculated from the Spanish Statistical Office, INE by its acronym in Catalan, data 2015).

The paper is organized as follows. In the following two sections, we describe the data as well as our estimation strategy. Finally, in the last two sections, we discuss the empirical results and draw some conclusions.

2 Data description

2.1 Study area

The dataset is at the NUTS3 level over the time span 2005Q1-2013Q4. More precisely, Spain is made up of 17 autonomous communities and 2 autonomous cities (Ceuta and Melilla) which together represent the first-order administrative division (NUTS2) of the country. Autonomous communities comprise provinces, i.e., groups of municipalities recognized by the constitution, of which there are 50 in total (NUTS3). In this work we use Spanish data at province level (i.e. 48 provincesFootnote 1 of 17 autonomous communities) from 2005 to 2013, obtained from the INE (2015).

2.2 Data

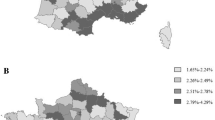
We analyse the occurrence of bankruptcy situations in Spain distinguishing between three different sectors: Agriculture, Industry and Services. This data is directly available at INE (2015) which provides the quarterly bankruptcies at province level. Figures 1, 2. 3 show how the annual mean of the bankruptcies occurred in the analysed period is distributed across the study area, distinguishing between the three considered sectors. One observes important differences between the Agriculture sector and the other two, being bigger in the central regions of Spain. Of course, most of the bankruptcies are in the more densely populated urban areas, namely Madrid, Barcelona and Valencia.

In order to better explain bankruptcy fluctuations, some macroeconomic variables have been included in the analysis. We use the real economic growth and real income per capita as indicators of business cycle and economic conditions, respectively. Furthermore, in order to control for agglomeration and size factors, the county population is also considered. Since seasonal effects might be expected, quarterly dummies are incorporated in all specifications. Finally, the intersectoral relationship is also tested.

Fig. 1
figure 1

Average annual bankruptcy rate in Agriculture sector

Full size image
Fig. 2
figure 2

Average annual bankruptcy rate in Industry sector

Full size image
Fig. 3
figure 3

Average annual bankruptcy rate in Service sector

Full size image

3 Methods

3.1 Statistical framework

Spatio-temporal data can be idealized as realizations of a stochastic process indexed by a spatial and a temporal dimension

$$\begin{aligned} \mathrm{Y}\left( \mathrm{s,t}\right) \equiv \mathrm{\{}\mathrm{y(s,t)|(s,t)}\in \mathrm{D\times T}\in {{\mathbb R}}^{\mathrm{2}}\mathrm{\times }{\mathbb R}\mathrm{\}} \end{aligned}$$
(1)

where \(\mathrm{D}\) is a (fixed) subset of \({{\mathbb R}}^{\mathrm{2}}\) and \(\mathrm{T}\) is a temporal subset of \({\mathbb R}\). The data can then be represented by a collection of observations \(\mathrm{\ \ y=}\mathrm{\{}\mathrm{y}\left( {\mathrm{s}}_{\mathrm{1}},{\mathrm{t}}_{\mathrm{1}}\right) \mathrm{,\dots ,y}\left( {\mathrm{s}}_{\mathrm{i}},{\mathrm{t}}_{\mathrm{j}}\right) \}\), where the set \((s_1,..., s_i)\) indicates the spatial locations, at which the measurements are taken, and \((t_1,..., t_j)\) the temporal instants.

In our case we assume separability in the sense that we model the spatial correlation by the Matérn spatial covariance function and the temporal correlation using a random walk model of order 1 (RW1).

3.2 The model

The model used in this paper is a spatio-temporal model and it is used to estimate the number of events (bankruptcies in our case) per unit area (\(s_i\)) and occurred in a specific time (\(t_j\)), following the structure used in (Blangiardo and Cameletti 2015).

Then, assuming that the subscript i (\(i=1,...,48\)) denotes the province where the bankruptcies have occurred, the subscript j (\(j=1,...,17\)) represents the autonomous community level, k (\(k=1,2,3\)) is the sector considered and t (\(t=2005,...,2013\)) is the time when they happened, we specify the log-intensity of the Poisson processes by a linear predictor (Illian et al. 2012) of the form:

$$\begin{aligned} \eta _{ijkt}(s_{i})= \beta _{0}+\sum _\alpha \beta _\alpha z_{\alpha _{i}}+\beta z_{j}+ \sum _{\phi \ne k} \delta _{\phi } lag_{k}(y_{i,j,\phi ,t}) + S_{i}+{\tau }_{t} \end{aligned}$$
(2)

where \(\beta _{0}\) is a scalar which represents the intercept, \(\beta _\alpha \) are the coefficients which quantify the effect of the covariates considered \(z_{\alpha _{i}}\) on the response at the province level (population) and \(\beta \) is the coefficient of the covariates at the autonomous community level (growth and income). In order to analyse the inter-sector relationship, the model also includes two variables representing the bankruptcies occurred in the other two sectors which are characterized by the variables \(lag_{k}(y_{i,j,\phi ,t})\) and have associated the coefficients \(\delta _{\phi }\), with \(\phi \ne k\).Footnote 2 Specifically, we have considered the temporal lag of these variables as it has been tested an improvement in the estimation of the model when it was considered. The number of lags depends on the sector analysed and has been determined examining the lower value of the Normalized Root Mean Square Error (NRMSE) of each model. We have considered up to a maximum of two years. In particular, for the Agriculture sector the lag considered has been one year and a half and for the Industry and Services two years.

In addition, two random effects are also introduced: (i) spatial dependence, \(S_i\) and (ii) temporal dependence, \({\tau }_t\). So it is considered that our dependent variable can be different for each region and may vary during the period under analysis. The temporal dependence is assumed smoothed function, in particular, an autoregressive model of order 1 (ar1) for the Agriculture sector and a random walk of order 1 (RW1) for the other two sectors. The SPDE technique is used to model spatial dependence because of its versatility and the novelty of this methodology. It is more flexible than other models such as iCAR, BYM, or Leroux CAR models (Jarvis et al. 2019; Jaya and Folmer 2020, 2021), and allows the researcher to incorporate neighbouring structures. For instance, CAR was thought for regular lattice, and it had some problems when this is irregular and/or the‘cells’are very different in the area. This is not the case for the SPDE approach based, precisely, on the irregular (or very irregular) lattice. In addition, CAR’s correlation is a constant but in SPDE correlation is a function of the distance between areas (Wall 2004; Bakka et al. 2018). Moreover, if the spatial correlation interaction between the nonstationary parameter fields is ignored, the SPDE approach allows us to extend the stationary example to nonstationary while the other models become limited. Then, for non-stationary spatial models and nonseparable space-time models, as is our case, minor tweaks to the SPDE technique result in straightforward approaches making possible the modelization.

Typically, when dealing with count data a Poisson model is assumed for modelling its distribution or, at least, approximating it. However, when there are too many zero counts in the observations, then the dispersion of the Poisson model underestimates the observed dispersion. Mixed-distribution models, such as the zero-inflated Poisson (ZIP), are often used in such cases. In this work, the response variable that we are taking into account is the number of bankruptcies at the province level distinguishing between the three sectors considered (Agriculture, Industry and Services) and, because of the number of zeros of bankruptcies in the Agriculture sector, this variable, unlike the other two, is modelled by following a Zero-inflated Negative Binomial of type 2. The other two sectors do not present this kind of data and so a Poisson model is assumed for modelling the distribution of the count observation.

Models are estimated by employing the Integrated Nested Laplace Approximation (INLA) algorithm. This innovative and recent approach is used within a Bayesian framework and makes possible the transformation from a Gaussian field (GF) to a Gaussian Markov Random Field (GMRF). In addition, when dealing with Bayesian inference for GMRFs it is possible to use the INLA algorithm proposed by (Rue et al. 2009) as an alternative to Markov chain Monte Carlo (MCMC) methods for latent Gaussian field models giving rise to addition computational advantages. This class of space-time models have the remarkable feature to be flexible and time-efficient. All analyses are carried out using the R freeware statistical package (version 4.1.0) (2011) and the R-INLA package (2019).

3.3 Statistical inference

3.3.1 SPDE approach

When dealing with spatio-temporal geostatistical data and assuming separability, we need to specify a valid spatio-temporal covariance function defined by \(Cov\left( y_{it},y_{jq}\right) ={\sigma }^2_CM\) where \({\sigma }^2_C>0\) is the variance component and M is the Matérn spatio-temporal covariance function, which controls the spatial correlation at distance\(\ \left\| h\right\| =\left\| s_i-s_j\right\| \) and is given by

$$\begin{aligned} M\left( h\mathrel {\left| \right. }\nu ,\kappa \right) =\frac{2^{1-\nu }}{\Gamma \left( \nu \right) }{\left( \kappa \left\| h\right\| \right) }^{\nu }{\mathrm{K}}_{\nu }(\kappa \left\| h\right\| ) \end{aligned}$$
(3)

where \({\mathrm{K}}_{\nu }\) is a modified Bessel function of the second kind and \(\kappa >0\) is a spatial scale parameter whose inverse,\(\ 1/\kappa \), is sometimes referred to as a correlation length. The smoothness parameter \(\nu >0\) defines the Hausdorff dimension and the differentiability of the sample paths (Gneiting et al. 2010). Specifically, we tried \(\nu \)=1,2,3 (Plummer and Penalized 2008).

Using the expression defined in (3), when \(\nu +d/2\) is an integer, a computationally efficient piecewise linear representation can be constructed by using a different representation of the Matérn field \(\ x\left( s\right) \), namely as the stationary solution to the stochastic partial differential equation (SPDE) (Simpson et al. 2011)

$$\begin{aligned} {{(\kappa }^2-\triangle )}^{\alpha /2}x\left( s\right) =W(s) \end{aligned}$$
(4)

where\(\ \ \alpha =\nu +d/2\) is an integer, \(\ \ \triangle =\sum ^d_{i=1}{\frac{{\partial }^2}{\partial s^2_i}}\) is the Laplace operator and W(s) is spatial white noise.

The basic idea is that, the SPDE approach allows to represent a Gaussian Field with the Matérn covariance function defined in (3) as a discretely indexed Gaussian Markov Random Field (GMRF) by means of a basis function representation defined on a triangulation of the domain D,

$$\begin{aligned} \mathrm{X}\left( \mathrm{s}\right) \mathrm{=}\sum ^{\mathrm{n}}_{\mathrm{l=1}}{{\varphi }_{\mathrm{l}}{\mathrm{(s)}\omega }_{\mathrm{l}}} \end{aligned}$$
(5)

where n is the total number of vertices in the triangulation, \(\left\{ {\varphi }_{\mathrm{l}}\mathrm{(s)}\right\} \) is the set of basis function and \(\left\{ {\omega }_{\mathrm{l}}\right\} \) are zero-mean Gaussian distributed weights. The basis functions are not random, but rather are chosen to be piecewise linear on each triangle

$$\begin{aligned} {\varphi }_{\mathrm{l}}\left( \mathrm{s}\right) \mathrm{=}\left\{ \begin{array}{c} \mathrm{1\ \ \ \ \ \ \ \ \ \ \ \ \ \ at\ vertix\ l} \\ \mathrm{\ \ \ 0\ \ \ \ \ \ \ \ \ \ \ }\mathrm{\ \ \ elsewhere\ \ \ } \end{array} \right. \end{aligned}$$
(6)

The key is to calculate the weights \(\mathrm{\ \ }\left\{ {\omega }_{\mathrm{l}}\right\} \), which reports on the value of the spatial field at each vertex of the triangle. The values inside the triangle will be determined by linear interpolation (Simpson et al. 2011).

Thus, the expression (5) defines an explicit link between the Gaussian field X(s) and the Gaussian Markov random field, and it is defined by the Gaussian weights \(\left\{ {\omega }_l\right\} \) that can be given by a Markovian structure. This, in turn, produces substantial computational advantages (Lindgren et al. 2011).

The temporal dependence (on t) is modeled through a smoothed function, namely a RW1 (2019). Thus, RW1 for the Gaussian vector \(x=(x_1,\dots ,x_n)\) is constructed assuming independent increments

$$\begin{aligned} \triangle x_i=x_i-x_{i-1}\sim N(0,{\tau }^{-1}) \end{aligned}$$
(7)

The density for x is derived from its \(\ n-1\) increments as

$$\begin{aligned} \pi \left( x\mathrel {\left| \right. }\tau \right) \propto {\tau }^{{\left( n-1\right) }/{2}}exp\left\{ -\frac{\tau }{2}\sum {{\left( \triangle x_i\right) }^2}\right\} ={\tau }^{{(n-1)}/{2}}exp\left\{ -\frac{1}{2}x^TQx\right\} \end{aligned}$$
(8)

where \(Q=\tau R\) and R is the structure matrix reflecting the neighbourhood structure of the model (2019).

By default, the prior on the intercept and the coefficients for fixed effects are a Gaussian with zero mean and precision 0.001, and the prior on the precision of the error terms are a Gamma with parameters 1 and 0.00005.

4 Results and discussion

The results illustrate the spatial spillovers of bankruptcy occurrence among Spanish counties. The exponential transformation of variable coefficients can be interpreted as elasticities. The Deviation Information Criterion (DIC) is an indicator of goodness of fit of each model or specification. So, for each model we comment and present only the specification with the smallest value of this indicator.

Table 1 Summary statistics (Data: 2005Q1-2013Q4)
Full size table

The descriptives of the variables used are given in Table 1. There are shown the mean and the standard deviation of our covariates.

Table 2 Results of INLA Random Effects models; dependent variable = Agriculture; \(N=1764\)
Full size table

Depending on the covariates included in the model, three different models for each of the three sectors considered have been constructed. They are represented in the columns entitled I; II and III in Tables 2, 3 and 4. The first model does not consider seasonal effects, the second one includes all the covariates and the third does not include the real economic growth.

Table 2 shows the findings related to the Agriculture model. It is confirmed the presence of spatial variability (0.027, 0.064 and 0.030 according to each estimated model respectively). The temporal variability (0.3722, 0.3799 and 0.3711 according to each estimated model respectively), which is quite important, is also detected being both of them statistically significant. This finding demonstrates that the bankruptcy rate in the Agriculture sector is determined by a spatiotemporal structure in which the temporal dimension seems to be more important than the spatial one. Surprisingly, the business cycle, proxied by Growth variable, seems to have no effect on bankruptcy occurrences. This result can be due to the fact that the model already controls for past fluctuations. So, the business cycle could be incorporated in the inertia of the process. The county population is positively correlated with the number of bankruptcies. In other words, a 1\(\%\) increase in population leads to an increase in bankruptcies by 0.316\(\%\) looking at the third model (III) (the smallest DIC value). Notably, real income per capita shows a negative impact on business defaults: a one-percent raise in income per capita causes a reduction in firms’ default by 0.066\(\%\).

Table 3 Results of INLA Random Effects models; dependent variable = Industry; \(N=1764\)
Full size table

The intersectoral relationship is captured by the inclusion of the number of bankruptcies in the Industry and Services sectors. The findings show that there do not exist any intersectoral effects (as there are no significant coefficients of these two variables in any of the three estimated models). So, a shock in the number of defaults in these two sectors do not impact the Agricultural sector. We interpret this result as evidence of lack of spillover effects from Industry and Service sectors to Agriculture.

Regarding Table 3, one can see that the findings related to the Industry sector are similar to the previous ones. Again, we observe the presence of both spatial and temporal variability even if the temporal effect is less remarkable than in the Agriculture sector. Unlike the Agriculture sector, the two dimensions now show a similar magnitude. Then, also the county population has an effect, a one per cent increase in population drives to an increase in bankruptcy rate by 0.990\(\%\) looking at the second model (II) (the smallest DIC value). As before, we do not find any intersectoral relationship as documented by the non-significance of the variable“Agriculture”and “Services”.

Table 4 Results of INLA Random Effects models; dependent variable = Services; \(N=1764\)
Full size table

Finally, in Table 4 we have the findings related to Services sector specifications. Here, a 1\(\%\) increase in county population leads to an increase in bankruptcy rate by 0.881\(\%\) looking at the second model (II) (the smallest DIC value). In contrast with the previous models, a one-percent increase in agricultural bankruptcy rate causes an increase in the number of default in Services sector by 0.021\(\%\). A raise by 1\(\%\) in the default rate of Industry sector increases the number of bankruptcies of Services sector by 0.001\(\%\). We interpret these findings as empirical evidence of the existence of intersectoral spillover effects from the Agriculture and Industry sectors to the Services sector. This means that in a given region an increase in the number of failures in the Agriculture and Industry sectors leads, ceteris paribus, to an increase in the number of bankruptcies in the Services sector.

In addition, according to the findings of Table 4, the Services sector is affected by temporal and spatial with a slight prevalence of the latter over the former.

It has been observed that although in all sectors there is both spatial and temporal variability, in the case of Agriculture the temporal variability is very noteworthy. This fact could be explained given the dependence of this sector on meteorological conditions or availability of natural resources, which can vary from one year to another (dar and dar 2021; Fanelli 2020).

The knowledge of intra and inter-sector spillover effects is of extreme importance in order to understand how bankruptcy rates propagate over time and space. Few recent contributions have tried to analyse this issue by focusing on a single industry (Le and Ngo 2020; Nguyen 2019). This paper goes further by considering three main sectors in order to establish the propagation effects across them. We observe an unidirectional spillover effect going from both Agriculture and Industry to Services sector. The latter is highly diverse accounting for a number of activities like infrastructure services, financial services, business services, social services, etc. This aspect could explain why the Services sector is highly affected by what happens in the other two sectors, namely Industry and Agriculture since they represent an important component of the demand for services. This result has an important implication. The Services sector seems to be sensitive to the cyclical fluctuations of other sectors. Unfortunately, data limitation does not allow us to explore which sub-sector is affected the most. Thus, it remains an issue for future researches.

5 Final remarks

This paper aims to study the spatial and intersectoral spill-overs in aggregate failure rates using Spanish regions as case-study in the time span 2005Q1-2013Q4. For this purpose, we employ a space-time model, by means of the Integrated Nested Laplace Approximation (INLA) approach.

The empirical analysis documents the presence of temporal and spatial spill-overs in all three sectors considered, namely Agriculture, Industry and Services. Furthermore, intersectoral spill-over effects are observed only in Services sector. In other words, we find that bankruptcy fluctuations in Industry and Agriculture sectors positively affect the default rate of the tertiary sector.

Such result has important policy implications. We document the existence of bankruptcy contagious both in spatial and intersectoral dimension, which means that a shock in the number of defaults in a region or in a sector could easily be transmitted to another sector and/or neighbouring region. The knowledge of such potential propagation and its channels is extremely important to set up opportune policy rules in order to reduce and shrink the contagion during an economic crisis.