Abstract
In a horizontally differentiated duopoly, a green attribute (environmental quality) can be added to the products. Average green quality generates a positive externality entering the Government’s objective function (and possibly consumers’ utility). A tax on the “dirtiest” product decreases its environmental quality but it increases that of the cleaner rival enough to imply an average quality increase, achieving environmental protection. The same holds for a subsidy to production targeted to the cleanest producer. A generic quality-related subsidy also increases the positive externality, increases profits of the greenest and lowers those of the dirtiest producer. Education campaigns by the Government also increase average green quality.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Governments and consumers worldwide are increasingly trying to foster sustainable production and consumption—for a discussion—see Nyborg et al. (2006). Often this implies enhancing a positive externality; one instance is the encouragement of product design aimed at recyclability, durability, waste reduction, as for example for electronics hardware (Hong and Ke (2011) discuss California legislation concerning smartphone producers).Footnote 1 Utilization of processes that do not damage the bumble bee (Smith et al. 2013) are also an example of a positive externality, as much as pesticide-free farming in general, antibiotic-free fish farming, and the likes. If this is the case, the positive externality may enter either both: the consumer utility function and the objective function of Governments, or just the latter. A single consumer, being of negligible size, cannot affect the overall externality, contrary to the Government, but consumers are found to be willing to pay for increased eco-compatibility (e.g. Moon et al. 2002), so that the green attribute, if not also the externality, enters their utility function. The aim of this article, then, is to explore the impact of tax-subsidy policies aimed at increasing the positive externality in a duopoly model of differentiated products.
A vertical product differentiation duopolyFootnote 2 is the reference model for Moraga-Gonzalez and Padron-Fumero (2002) who analyze anti-pollution emission standards and taxes. Among other results, they show that discriminatory (firm-specific) tax treatment of the dirtier product leads to a decrease in total emissions, contrary to what happens with a uniform tax rate, while reducing consumer surplus. Quite interestingly, they find that a standard on emissions leading to an increase in the quality of the lowest quality product, decreases per unit emissions but increases equilibrium sales and therefore reduces welfare. This is due to the interaction of quality choices, price to quality ratios, and demand effects. When qualities are exogenous,Footnote 3 as in Kurtyka and Mahenc (2011), the effect of a tax is in line with intuition and improves welfare, but when qualities are endogenous counterintuitive results are not uncommon, as in Moraga-Gonzalez and Padron-Fumero (2002) and Toshimitsu (2010) who finds that a subsidy to consumption of the green variant of product degrades the environment. This is due to the incentives on quality choice at the first stage of the competition process. Lombardini-Riipinen (2005) also uses a duopoly model with vertical differentiation and considers the effects of taxes on emissions when the marginal cost of firms is increasing in the emission abatement effort. Abatement generates a positive externality, entering the utility of consumers and the author discusses the policy tools addressing both the imperfect competition distortion and the environmental distortion.Footnote 4 Most of the models dealing with a first stage where quality or abatement is chosen share the common feature that differentiation is purely vertical, with the two firms producing goods that are otherwise identical in their horizontal dimension. In the present paper (as in Conrad 2005) firms produce goods that have a different appeal to consumers regarding both, the horizontal attribute (which only has private value to each consumer) and the environmental quality attribute.Footnote 5 This two-dimensional (with horizontal and vertical attributes) approach allows a wider range of situations than the pure vertical differentiation. In the same vein, a related paper is Deltas et al. (2013), where two firms produce horizontally differentiated goods with asymmetric intrinsic values; each firm can add an extra green attribute; in their model the exogenous intrinsic value asymmetry explains why increasing consumer green awareness may distort firms’ incentives to increase the green quality. In particular, the low quality firm may decrease its green quality when an education campaign by the Government increases the consumer green awareness; also, the high quality firm decreases its own quality when a Minimum Quality Standard is introduced. These effects are related to the equilibrium market shares dependence upon the asymmetric intrinsic values. Consumer awareness is also treated in Garcia-Gallego and Georgantzis (2009).
In general, therefore, these works show that policy instruments affect environmental qualities depending on how the investments in green quality at the first stage of the game are affected. In this respect, the two-dimensional approach here adopted also has some strongly appealing technical features. In particular, the best reply functions of the firms in the stage where they choose qualities are easily defined and regular, while this is never the case in the models with pure vertical differentiation.Footnote 6 Remarkably, as Ronnen (1991) shows, under pure vertical differentiation the quality of the highest quality firm increases as the lowest quality is increased; in the present context by contrast qualities are strategic substitutes, and the high quality increases if the low quality decreases, with important consequences on the resultsFootnote 7.
The model is a modified Hotelling linear city of unit length. An increase in the environmental quality absorbs extra-resources in the form of ex-ante development costs (the firm must buy new equipment or retool old one) and it implies a fixed cost. The two firms differ in their ability to obtain a quality improvement, so that the same quality level is more costly to reach for one of the two firms - the “low quality” firm. The game played by the two firms is the following. At the first stage firms choose their environmental quality level and pay the corresponding fixed cost. At the second stage firms choose prices.
The Government aims at discouraging the use of the “low quality” product as it is the one that deteriorates the average quality (deteriorates the external effect). The easiest way to do so is that of taxing the good of inferior quality, if one exists. A second way is that of introducing a subsidy for the production of the good of superior quality. Asymmetric taxes (or subsidies) can be applied by lifting the tax (granting the subsidy) if the product meets some pre-specified level of “greenness” (e.g. recyclability). This is a more modest aim for a policy than that of addressing at the same time also the price distortion, but it can be the one achieving political priority if the externality reaches dramatic consequences in the medium-long run (think again of the problem of insufficient bees reproduction). It is also possible to analyze a generic quality-related subsidy going to both firms; this policy is also shown to increase the positive externality, though not necessarily the quality of the dirtiest producer, to increase the quality difference between firms, with higher profitability limited to the greenest producer. An education campaign that increases consumer awareness to the green attribute is also shown to lead to a higher positive externality.
2 The model and equilibrium
Two firms produce goods that are horizontally differentiated with the two firms located at the opposite endpoints of a Hotelling linear city (Hotelling 1929) of unit length; consumer mass is also assumed to be equal to 1. Firms add to their product a desirable “green” attribute. Consumers value the green attribute in that they are ready to pay more for a product with a higher value of the parameter \(\theta\) representing the environmental quality. Firms are heterogeneous, in the sense that firm 1 is more skilled than firm 2 in using resources necessary to raise the value of \(\theta\). The total cost functions are \(C_{1}(q_{1},\theta _{1})=cq_{1}+\theta _{1}^{2}/2\), where \(c>0\) and \(C_{2}(q_{2},\theta _{2})=cq_{2}+\beta \theta _{2}^{2}/2\), where \(\beta >1\) is a cost parameter that distinguishes firm 2 from 1. As it appears from these cost functions, the quality \(\theta\) only affects fixed costs, as in much of the existing literature. Firms set prices \(p_{1}\) and \(p_{2}\) and resulting demands are \(D_{i}(p_{1},p_{2})\). It is useful to define \(\theta ^{a}=D_{1}\theta _{1}+D_{2}\theta _{2}\) as the average quality, where \(D_{1}+D_{2}=1.\)
A consumer location is identified by the real number \(x\in \left[ 0,1\right]\). When buying from firm located at \(x_{i}\), for \(x_{i}\in \{0,1\}\), a consumer bears a ‘transportation cost’, or a loss in utility respect to her own preferred brand. This loss in utility is measured by a money equivalent value of \(t\left| x-x_{i}\right|\), where t (or rather 1/t) represents the ability of a consumer to substitute between the two products. We shall denote by \(\tilde{x}\) the consumer who is indifferent between the two products. Then, letting \(d_{i}=|x-x_{i}|\), given the prices \(p_{1}\) and \(p_{2}\), the utility function is
where v is the intrinsic value of a good and \(\rho \ge 0\) is a taste parameter. The environmental quality \(\theta _{i}\) increases the value of good i, as it is the case, for instance, with increased repairability/recyclability of hardware, which increases durability while reducing waste, or with lower pesticide content, which makes the food healthy while reducing harm to biodiversity and water quality. A higher average \(\theta ^{a}\) increases the environmental positive externality; notice that since the market in equilibrium shall be always covered, average quality and “total” quality are in a one-to-one correspondence. Average quality \(\theta ^{a}\) can affect consumer utility if \(\rho >0\), as in Cremer and Thisse (1999), who also use average quality, or Bansal and Gangopadhyay (2003) and Koonsed (2015) who use an aggregate level of externality that cannot be affected by the individual consumer. If \(\rho =0\) the externality does not affect utility while the green attribute of the consumed unit does so through \(\theta _{i}\)—similar then to Arora and Gangopadhyay (1995). What really matters is that the externality enters the objective function of the Government, to be detailed in Sect. 3 below, which is therefore assumed to contain an additive element, denoted \(\zeta \theta ^{a}\), with \(\zeta >0\).
Firms compete in two stages: at the first stage they simultaneously choose their quality levels \(\theta _{1}\) and \(\theta _{2}\), and pay the relative costs of achieving those qualities; at the second and final stage firms simultaneously choose their prices.
Assumption 1 (i) \(t>2/9\), and (ii) \(v>2t+c\).
This assumption ensures that both quality levels are positive in equilibrium and that the market is fully covered. Consider that a single consumer has no effect on average quality; this is reflected in the derivation of demand functions. The consumer indifferent between buying at one or the other firm has address denoted \(\tilde{x}\) such that:
The demand functions at the second stage are \(D_{1}(p_{1},p_{2};\theta _{1},\theta _{2})=\tilde{x}\) and \(D_{2}(p_{1},p_{2};\theta _{1},\theta _{2})=1-\tilde{x}\). Then, the profit maximization problem for firm i at the second stage can be written as
Where \(\beta _{1}=1\) and \(\beta _{2}=\beta >1\). This provides the best reply function as \(\check{p}_{i}(p_{j})=\max \left\{ p_{j}/2+\left( (\theta _{i}-\theta _{j})+c_{i}+t\right) /2,0\right\}\).
Assume without loss of generality that \(\theta _{1}>\theta _{2}\) in a no tax equilibrium. Let \(c_{1}=c_{2}=c\). Then the Nash prices at the second stage as functions of the values for the \(\theta ^{\prime }s\) are
Notice that \(p_{2}^{*}(\theta _{1},\theta _{2})-p_{1}^{*}(\theta _{1},\theta _{2})=(2/3)(\theta _{2}-\theta _{1})\) is negative if the quality of firm 1 is higher than that of firm 2. The equilibrium demand functions are \(q_{i}^{*}=(p_{i}^{*}-c)/(2t)\) or
The low quality good 2 can be shown to be consumed in excess to the social optimum, since the optimal allocation would be with consumers at the left of \(x^{*}=\frac{\left( t+\theta _{1}-\theta _{2}\right) }{2t}\) consuming the high quality good 1.
The reduced form profits, that shall be used to solve the first stage of the game, are \(\pi _{i}^{*}=\left( t+(\theta _{i}-\theta _{j})/3\right) ^{2}/(2t)-\beta _{i}(\theta _{1})^{2}/2\) .
Firm 1 and firm 2 maximization program at the first stage give the best reply functions
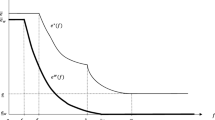
The two best reply functions in qualities are represented in Fig. 1 as two downward sloping straight lines assuming \(t>2/9\). Vertical qualities are strategic substitutes. Note that firm 2, say, cannot choose a quality lower than \(\theta _{1}-3t\) otherwise it is priced out of the market at the second stage, this explains the V-shape of its best reply function. The same holds true for firm 1, although, for illustrative purposes, the figure is drawn as if this firm were not concerned with being priced out.
If the best reply functions cross where they are both downward sloping then both firms shall enjoy a positive market share at equilibrium, with positive prices (irrespective of profits). Letting \(B=(9\beta t-\beta -1)\) one obtains, then, the Nash equilibrium values for the environmental qualities,
As expected, \(\theta _{1}^{*}>\) \(\theta _{2}^{*}\). Prices in equilibrium are:
It is possible that if t is too high, then the market shares of the two firms do not overlap and they behave as separate monopolists. To exclude this possibility it is assumed that even for consumer with address \(x=0\) one has \(u_{2}>0\) at an equilibrium, so that consumers buy from firm 1, eventually, because it gives a higher utility and not because they have no positive utility from the alternative offered by firm 2. This is true if the inequality \(v+\theta _{2}^{*}-p_{2}^{*}>t\) holds, as is guaranteed by part (ii) in A.1Footnote 8.
Therefore, under A.1 the best reply function in qualities of the two firms cross where they are both downward sloping. Average quality is: \(\bar{\theta } ^{*}=\theta _{1}^{*}D_{1}^{*}+\theta _{2}^{*}D_{2}^{*}\) or
The equilibrium profits for the benchmark case are,
Under the assumptions that \(t>2/9\) and \(\beta >1\) both profits are nonnegative, and that of firm 1 is always larger than that of firm 2.
3 Taxing the low quality product
If a Government taxes the low quality product it will raise the cost of production for the low quality from c to \(c+\tau =c_{2}\). A tax that is borne only by the low quality firm can be set by granting a tax exemption above a specified quality level (for instance a given percentage of recoverable material in an electronic device) that is satisfied by the high but not by the low quality producer. The model is meaningful when the asymmetry between firms is sizeable, namely when the quality difference is not so small as to be insufficient to justify a tax difference. In the real world, some firms are simply unable to improve quality above a level due to the technology used in production, or to the product design (which is different across firms—for instance, recyclability and reusability are better achieved by using modularity with some producers tied to non-modular designs). Taxing the non-fulfillment of some standard is then equivalent to taxing specific firms. Also, the greenest producer may be subject to a lower but positive tax rate when the products are taxed according to environmental categories; in our model the tax rate for that producer is zero. The price best reply of the taxed firm (firm 2 in our case) will shift upward and both equilibrium prices (at given qualities) will increase. In the end one obtains
Solving for the best replies in qualities: \(\theta _{1}^{\tau }=\left( 9t\beta +3\beta \tau -2\right) /(3B)\) and \(\theta _{2}^{\tau }=\left( 9t-3\tau -2\right) /(3B)\).
If \(\beta\) is not too high it is possible that firm 2 finds it optimal to try and leapfrog firm 1 in order to avoid the tax. This deviation from equilibrium is prevented for \(\beta\) large enough. The analytical details are thorny, and shall not be fully developed here. A sketch of the argument is that there may exist a value \(\theta _{2}^{\prime }>\theta _{1}^{\tau }\) that maximizes 2’s profits with firm 1 paying the tax and choosing \(\theta _{1}^{\tau }\) and firm 2 avoiding the tax. At the second stage \(p_{1}=t+c+\left( \theta _{1}^{\tau }-\theta _{2}+2\tau \right) /3\) and \(p_{2}=t+c+(\theta _{2}-\theta _{1}^{\tau }+\tau )/3\).
The valueFootnote 9 for \(\theta _{2}^{\prime }\), letting \(1/(3B-27Bt\beta )=L\) is \(\theta _{2}^{\prime }=L2+\) \(3L\left( B\tau -3t\beta -\beta \tau +4Bt\right)\). This deviation by firm 2 at the first stage could upsetFootnote 10 the equilibrium with \(\left( \theta _{1},\theta _{2}\right) =\left( \theta _{1}^{\tau },\theta _{2}^{\tau }\right)\). Obviously, however, \(\left( \theta _{1}^{\tau },\theta _{2}^{\prime }\right)\) cannot be an equilibrium, since \(\theta _{1}^{\tau }\) is not then a best reply by firm 1 to \(\theta _{2}^{\prime }\). It can be shown that for \(\tau =0\) this deviation is never profitable and the equilibrium is locally robustFootnote 11. As \(\tau\) increases enough a deviation can be profitable for \(\beta\) close enough to 1. We maintain that our analysis is valid under the proviso that there is enough asymmetry between firms.
The equilibrium qualities under a unit tax equal to \(\tau\), are found to be
Remark 1
The two qualities move in opposite direction and hence the effect on average quality will depend on the effects on market shares.
This is why the analysis is warranted: the deterioration in the quality of firm 2 could outweigh the benefits coming from the improvement of the other. The final effect will depend upon the final weights, namely the quantities demanded, attached to each quality. The effects on prices, quantities and on the average quality are computed as follows. The final price-vector will be:
Profits with a tax on the low environmental quality product are:
It can be verified that the profit of firm 1 is increasing in \(\tau\) and that of firm 2 is decreasing in \(\tau\) (around \(\tau =0\)).
Average quality can be shown to be equal to
and it follows that:
Proposition 1
A tax on the low environmental quality producer lowers the quality produced by this producer and raises that produced by the rival; however, overall the positive externality in the market is increased.
Obviously a tax will lead to exit of the taxed firm—which would lead to monopoly—if it is too high; in particular, since the equilibrium quantity of firm 2 is \(q_{2}^{\tau }=t\beta \left( 9t-2-3\tau \right) /B\), it must be \(\tau <3t-\left( 2/3\right)\). Furthermore since \(\frac{\partial \theta ^{a\tau }}{\partial \tau }>0\) average quality is monotone increasing in \(\tau\). It is worth looking at the effects of the unit transportation rate, t, on the effectiveness of a tax. The parameter t is an index of (horizontal) competitiveness: the lower is t the higher the competitiveness. It can be shown that the marginal effect of a tax on average quality is decreasing in t. Indeed \(\partial ^{2}\theta ^{a\tau }/\partial \tau \partial t<0\).
Corollary 2
A higher competitiveness, as measured by the ratio 1/t, increases the effectiveness of a tax.
A Government may only aim at increasing the externality, or it may consider a more complete welfare function. Since prices are a transfer from consumers to firms and since the market in equilibrium shall be covered, the total welfare for the Government can be written as:
where \(T=\frac{t}{2}\left[ \tilde{x}^{2}+\left( \tilde{x}-1\right) ^{2} \right]\) is the total “transportation cost” (total disutility form buying a specification that is horizontally inferior to the best preferred one) borne by consumers.
Letting \(\lambda =\rho +\zeta\), from (3.7) one can rewrite the welfare function gross of transportation costs as:
and recalling that \(T=(1/2)[\tilde{x}^{2}t+t\left( \tilde{x}-1\right) ]^{2}\) one has
One can show that \(\frac{\partial W_{G}}{\partial \tau }\) is positive for \(\tau =0\) and that \(W_{G}\) is concaveFootnote 12. The same is true for the derivative of W as far as \(\lambda >\frac{ 2\beta -4}{\beta +1}\). Hence welfare is always increased by a tax around \(\tau =0\) and one could compute an optimal tax rate for both objective functions if \(\lambda\) is high enough.
4 Subsidizing the green attribute
4.1 A subsidy targeted to firm 1
If a Government subsidizes the greenest product it will lower the cost of production for firm 1 from c to \(c-\sigma =c_{1}\). The price best reply of this firm will shift downward and both equilibrium prices (at given green attributes) will decrease. Indeed:
Solving for the best replies in \(\theta ^{\prime }s\) and analyzing the average quality then provides the same results as for a tax on the low quality product, with \(\sigma\) replacing \(\tau\) in the expressions. The only difference is that a subsidy must be financed by taxing some income or goods and will produce a distortion that is not explicit in the partial equilibrium analysis. Similarly, it can be shown that a uniform ad-valorem tax reduces both qualities and therefore a uniform ad-valorem subsidy will increase both qualities and average quality as well. By contrast a uniform unit subsidy does not change prices and quantities and therefore is totally ineffective as it leaves qualities unchanged as well.
4.2 Quality dependent subsidy
A quality dependent subsidy scheme can also be envisaged, where the Government grants unit subsidy, as a function of the green attribute embedded in a product (as for instance, the percentage of recyclable components). When choosing qualities, firms will anticipate the reduction in marginal costs that will follow from an increase in the green attribute. The analysis is sketched below. The Government can grant a subsidy whereby a firm receives an amount equal to \(\sigma \theta _{i}\) for each unit produced—marginal costs are expressed as \(C-\sigma \theta _{i}\), restricting C and \(\sigma\) to have \(C-\sigma \theta _{i}>0\). It can be shown that the equilibrium environmental qualities are
where \(Z=6\sigma +3\beta -27t\beta +3\sigma ^{2}+6\sigma \beta +3\sigma ^{2}\beta +3\). Then it can also be shown that for all \(\beta >1\) and \(2/9<t<1\)the first derivative of \(\theta _{1}\) with respect to \(\sigma\) for \(\sigma =0\) is positive while that of \(\theta _{2}\) is negative if t is smaller than a thresholdFootnote 13 and positive otherwise—an increase in \(\theta _{1}\) may prevent the less efficient firm to increase its quality if the market is highly competitive.
Further, the difference \(\theta _{1}-\theta _{2}\) increases with \(\sigma\). It is interesting to note that:
Proposition 1
A quality dependent subsidy (at least locally) increases the positive externality as measured by average quality, it increases the profits of the greenest producer and damages the other.
The proof is not provided here and it is available upon request. The demandFootnote 14 to the greenest producer firm 1 increases as well as its unit margin, therefore its profit increases. The reverse results hold for firm 2.
5 Increasing consumer awareness
An education campaign by the Government to increase consumer awareness is an alternative method to foster the positive externality also analyzed in Deltas et al. (2013). In the present framework one can modify the utility function as
where \(\eta \ge 1\) represents a parameter that is increased by a campaign to inform consumers about the effects of their consumption choices and is therefore increasing with such a policy. Then one can show that the equilibrium prices at the second stage are \(p_{i}=c+t+\frac{1}{3}\eta \left( \theta _{i}-\theta _{j}\right)\), and the equilibrium green attributes, letting \(3\eta ^{2}-27t\beta +3\beta \eta ^{2}=K\) are
The quality level of firm 1 is increasing in \(\eta\). That of firm 2 can be decreasing around \(\eta =1\) (in particular, for low values of t in the admissible rangeFootnote 15). Demand to firm 1 is increasing as well as the quality difference. Average (and total) green quality is also increasing in \(\eta\). A full development of the effects of consumer awareness is, however, beyond the scope of the present note.
6 Conclusion
The introduction of subsidies or taxes to encourage the diffusion of goods with positive externalities is a widespread tool and a widely debated one. The present paper adopts a duopoly model with both a green quality attribute and horizontal differentiation. This allows a technically clear derivation of the effects of taxes and subsidies and it also allows the analysis of situations that do not fit the model of pure vertical differentiation. The problem here addressed is that of an underproduction of desirable attributes of products, due the presence of a positive externality. Addressing this issue can be urgent and of prior concern in real situations. The main results of the analysis are: that although a tax on the lowest quality product depresses the quality of this product in equilibrium, it generates a countervailing increase in the quality of the high quality product. This is due to qualities being strategic substitutes—a feature not shared by models of pure vertical differentiation. In the end, the average quality consumed increases and so the positive externality generated. Welfare is also increased by a tax on the low quality (a subsidy on the high quality). Also, a subsidy or a tax are more effective in markets where horizontal differentiation does not provide firms with great market power, as measured by the unit transport rate in the Hotelling line. A quality-dependent subsidy to producers benefits the more efficient firm in terms of ability to increase the green attribute and it hurts the other, but leads to higher quality and improves the externality. A Government education campaign that increases consumers ecological awareness (as in Deltas et al. 2013) also increases the positive externality.
Notes
As reported in Hong and Ke (2011): The state of California’s recent legislation (IWMB (Integrated Waste Management Board, California), 2003, Nixon and Saphores (2007)) initially assigns an advanced recycling fee (ARF) of $6–$10 on all electronic products containing hazardous materials and the ARF is used to fund an electronics recycling system (Gable and Shireman 2001) to compensate the processing costs incurred. In January 2009 the California ARF was increased to $8–$25 depending on screen size of the video display (SBOE 2009).
Kurtyka and Mahenc (2011) also assume that consumers are homogeneous as to the incremental value of the clean product, as in the case here considered.
Other works based on pure vertical differentiation duopoly are found in André et al. (2009) and Lambertini and Tampieri (2012) where qualities can take only two values and firms can be regulated to choose the high quality. Cremer and Thisse (1999) and Constantatos and Sartzetakis (1999) show that a uniform tax can increase the number of firms. Toolsema (2009) introduces switching costs.
This enters the utility function as a “vertical” attribute because it shares the property that “more is better” for all consumers (see e.g. Belleflamme and Peitz 2015 and Beath and Katsoulacos 1991 (p.109), for a definition of vertical differentiation). Degryse (1996) and Garella (2006) adopt a similar model.
As Moraga-Gonzalez and Padron-Fumero (2002) discuss, leapfrogging can occur and destroy the equilibrium—this may also happen in the present model as discussed in Sect. 3 below. In Lombardini-Riipinen (2005) quality best replies are not easily defined. For the case with no production costs see Wauthy (1996).
See also Garella (2006).
The desired inequality can be fully written as \(v+\left[ (9t-2)/(3B)\right] -2t-c+t\left[ (\beta -1)/B\right]\) where \(B=9\beta t-\beta -1\).
Demand to firm 2 is given by \(\frac{1}{2}+\frac{3B\tau -9t\beta +3B\theta _{2}-3\beta \tau +2}{18Bt}\).
The condition is \(\pi _{2}^{\tau }<\pi _{2}^{\prime }\) where \(\pi _{2}^{\tau }\) is given in (3.4) below, and the deviation profit to firm 2 is \(\pi _{2}^{\prime }=\beta \frac{\left( 3B\tau -9t\beta -3\beta \tau +9Bt+2\right) ^{2}}{18B^{2}\left( 9t\beta -1\right) }\).
The condition that ensures \(\pi _{2}^{\prime }>\pi _{2}^{\tau }\) when \(\tau =0\) is \(\left( 1-\beta \right) \left( 9t-2\right) \left( 9t\beta -1\right) >0\) which is imposisble for \(\beta >1\) under A.1.
Indeed \(\frac{\partial W_{G}}{\partial \tau }=\frac{\beta \left( 9t-2\tau -3t\beta +3t\lambda -2\beta \tau +3t\beta \lambda \right) }{2B^{2}}\) .
The value is \(t(\beta )=\frac{5\beta +\sqrt{-18\beta +17\beta ^{2}+1}-1}{ 18\beta }\) where \(\beta >1\).
The demand to firm 1 is \(\frac{1}{6t}\left( 3t+\theta _{1}-\theta _{2}-c_{1}+c_{2}\right)\) and the quality difference increases with the subsidy. Firm 1’ margin is \(t+\frac{1}{3}(1+\tau )\left( \theta _{1}-\theta _{2}\right)\).
Namely, since \(\frac{\partial \theta _{2}}{\partial \eta }\) has the same sign as \(2\eta ^{4}+81t^{2}\beta +9t\eta ^{2}+2\beta \eta ^{4}-45t\beta \eta ^{2}\) , for \(\eta =1\) the condition for \(\frac{\partial \theta _{2}}{ \partial \eta }>0\) is \(t>(18\beta )^{-1}\left( 5\beta +\sqrt{-18\beta +17\beta ^{2}+1}-1\right)\).
References
André, F.J., González, P., Porteiro, N.: Strategic quality competition and the porter hypothesis. J. Environ. Econ. Manag. 57(2), 182–194 (2009)
Arora, S., Gangopadhyay, S.: Toward a theoretical model of voluntary overcompliance. J. Econ. Behav. Organ. 28(3), 289–309 (1995)
Bansal, S., Gangopadhyay, S.: Tax/subsidy policies in the presence of environmentally aware consumers. J. Environ. Econ. Manag. 45(2), 333–355 (2003)
Beath, J., Katsoulacos, Y.: The Economic Theory of Product Differentiation. Cambridge University Press (1991)
Belleflamme, P., Peitz, M.: Industrial Organization: Markets and Strategies. Cambridge University Press (2015)
Conrad, K.: Price competition and product differentiation when consumers care for the environment. Environ. Resour. Econ. 31(1), 1–19 (2005)
Constantatos, C., Sartzetakis, E.S.: On commodity taxation in vertically differentiated markets. Int. J. Ind. Organ. 17(8), 1203–1217 (1999)
Cremer, H., Thisse, J.F.: On the taxation of polluting products in a differentiated industry. Eur. Econ. Rev. 43(3), 575–594 (1999)
Degryse, H.: On the interaction between vertical and horizontal product differentiation: an application to banking. J. Ind. Econ. 44(2), 169–186 (1996)
Deltas, G., Harrington, D.R., Khanna, M.: Oligopolies with (somewhat) environmentally conscious consumers: market equilibrium and regulatory intervention. J. Econ. Manag. Strategy 22(3), 640–667 (2013)
Gable, C., Shireman, B.: Computer and electronics product stewardship: are we ready for the challenge? Environ. Qual. Manag. 11(1), 35–45 (2001)
Gabszewicz, J.J., Thisse, J.-F.: Price competition, qualities and income disparities. J. Econ. Theory 20, 340–359 (1979)
García-Gallego, A., Georgantzís, N.: Market effects of changes in consumers’ social responsibility. J. Econ. Manag. Strategy 18(1), 235–262 (2009)
Garella, P.G.: Innocuous minimum quality standards. Econ. Lett. 92(3), 368–374 (2006)
Hong, I.H., Ke, J.S.: Determining advanced recycling fees and subsidies in ‘E-scrap’ reverse supply chains. J. Environ. Manag. 92(6), 1495–1502 (2011)
Hotelling, H.: Stability in competition. Econ. J. 39, 41–57 (1929)
Koonsed, P.: Optimal policy under duopoly with environmental quality. Econ. Bull. 35(3), 1976–1984 (2015)
Kurtyka, O., Mahenc, P.: The switching effect of environmental taxation within Bertrand differentiated duopoly. J. Environ. Econ. Manag. 62(2), 267–277 (2011)
Lambertini, L., Tampieri, A.: Vertical differentiation in a Cournot industry: the Porter hypothesis and beyond. Resour. Energy Econ. 34(3), 374–380 (2012)
Lombardini-Riipinen, C.: Optimal tax policy under environmental quality competition. Environ. Resour. Econ. 32(3), 317–336 (2005)
Moon, W., Florkowski, W. J., Brückner, B., and Schonhof, I. (2002). Willingness to pay for environmental practices: implications for eco-labeling. Land Econ., 78(1), 88-102, 317-336
Moraga-Gonzalez, J.L., Padron-Fumero, N.: Environmental policy in a green market. Environ. Resour. Econ. 22(3), 419–447 (2002)
Nixon, H., Saphores, J.D.M.: Financing electronic waste recycling Californian households’ willingness to pay advanced recycling fees. J. Environ. Manag. 84(4), 547–559 (2007)
Nyborg, Karine, Howarth, Richard B., Brekke, Kjell Arne: Green consumers and public policy: on socially contingent moral motivation. Resour. Energy Econ. 28(4), 351–366 (2006)
Ronnen, U.: Minimum quality standards, fixed costs, and competition. Rand J. Econ. 22, 490–504 (1991)
SBOE (State Board of Equalization), (2009). Electronic Waste Recycling Fee. http://www.boe.ca.gov/pdf/pub95.pdf.
Shaked, A., Sutton, J.: Relaxing price competition through product differentiation. Rev. Econ. Stud. 49, 3–14 (1982)
Smith, K.M., Loh, E.H., Rostal, M.K., Zambrana-Torrelio, C.M., Mendiola, L., Daszak, P.: Pathogens, pests, and economics: drivers of honey bee colony declines and losses. EcoHealth 10(4), 434–445 (2013)
Toolsema, L.A.: Interfirm and intrafirm switching costs in a vertical differentiation setting: green versus nongreen products. J. Econ. Manag. Strategy 18(1), 263–284 (2009)
Toshimitsu, T.: On the paradoxical case of a consumer-based environmental subsidy policy. Econ. Model. 27(1), 159–164 (2010)
Wauthy, X.: Quality choice in models of vertical differentiation. J. Ind. Econ. 44(3), 345–353 (1996)
Acknowledgements
The author thanks two anonymous referees for their helpful comments.
Funding
Open access funding provided by Università degli Studi di Milano within the CRUI-CARE Agreement. The author thanks the Portuguese Fundaçao para a Ciencia e a Tecnologia ref. NORTE-01-0145-FEDER-028540 and UIDB/04105/2020.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Garella, P.G. The effects of taxes and subsidies on environmental qualities in a differentiated duopoly. Lett Spat Resour Sci 14, 197–209 (2021). https://doi.org/10.1007/s12076-021-00272-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12076-021-00272-7
Keywords
- Product differentiation
- Oligopoly
- Environmental externality
- Positive externality
- Waste reduction
- Green tax
- Green subsidies