Abstract
We present a novel approach based on statistical permutation tests for pruning redundant subtrees from genetic programming (GP) trees that allows us to explore the extent of effective redundancy . We observe that over a range of regression problems, median tree sizes are reduced by around 20% largely independent of test function, and that while some large subtrees are removed, the median pruned subtree comprises just three nodes; most take the form of an exact algebraic simplification. Our statistically-based pruning technique has allowed us to explore the hypothesis that a given subtree can be replaced with a constant if this substitution results in no statistical change to the behavior of the parent tree—what we term approximate simplification. In the eventuality, we infer that more than 95% of the accepted pruning proposals are the result of algebraic simplifications, which provides some practical insight into the scope of removing redundancies in GP trees.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
It has long been accepted that genetic programming (GP) produces trees that contain substantial amounts of redundancy [2, 3, 10, 15, 30]. The objections to this are well rehearsed: the tree evaluation time is increased, and the redundant subtrees may obscure human interpretation of the evolved solution. It is therefore desirable to remove as much of this redundant material as possible. Although manual tree simplification has been used in the past [14], automated tree simplification is much preferred but is very challenging [31]; Naoki et al. [18] point out that canonical simplification is not Turing computable. Work on the simplification of GP trees has been reviewed by Kinzett et al. [13].
Nordin et al. [20] have defined a taxonomy of introns—broadly, the redundant code fragments that make no contribution to the tree’s overall fitness; some of these are noted to depend on particular test cases [10, 20]. Jackson [10] has addressed removal of a subset of introns, dormant nodes, that are never executed.
Zhang and co-workers [30, 31] have explored the use of hashing to simplify trees both at the end of a run as well as during the evolutionary run. These authors found, unsurprisingly, that simplification reduced tree sizes although the effect on test performance was not examined with any formal statistical procedure and does appear to have been resolved. Interestingly, Zhang and co-workers concluded that their initial hypothesis that frequent simplification would reduce genetic diversity and therefore hinder search proved unfounded; they did, however, find evidence against applying simplification at every generation.
In addition to exploring a hash table based approach to algebraic simplification, Zhang and co-workers [12, 25] have also examined approximate numerical simplification methods based on the local effect of a subtree. Kinzett et al. [12] replaced a subtree by the average of its output over the training set if the range of its outputs fell below a user-defined threshold. Song et al. [25] pruned trees by comparing the output of a binary node with its two inputs and replacing that node with either child if it gave the same value as the binary output within a threshold. The drawbacks with both these contributions are that: (i) they involve local operations that ignore the effect of an edit higher in the tree, and (ii) both rely on setting user-defined thresholds for which there appears to be no principled method other than trial-and-error. The shortcoming of ignoring the propagated effects of changes higher in the tree was examined by Johnston et al. [11] although they too used a two-stage process that relies on a user-defined threshold to gauge the acceptability (or otherwise) of a proposed simplification. Further, these authors only considered the propagated influence of a proposed simplification one or two levels up the tree.
Naoki et al. [18] have applied two simplification methods in tandem: one based on a set of rewriting rules derived from normal algebra (e.g. \(x \times 1 \rightarrow x\)), and a second using an approximate numerical method that compares the output of every subtree in a parent with the outputs of a small library of simple trees; if a library tree provides an ‘equivalent’ output to the subtree under examination and is simpler, the library tree is substituted. This second method was found to be particularly effective in reducing tree size, but suffers from a number of drawbacks: (i) the method again relies on a user-defined threshold to gauge similarity, and (ii) definition of the comparison library is domain-specific and potentially sensitive to the exact problem at hand.
Although the hash table based algebraic simplification of Zhang and co-workers and other rule-based approaches are interesting and illuminating contributions, they too suffer from a number of drawbacks. Principally, algebraic simplification is limited in scope and does not consider ‘effective’ redundancy [11]. For example, consider the expression \(x+\epsilon\) where x is of the order of unity and \(\epsilon\) is, say, \(10^{-32}\). To all intents and purposes, the result of this addition operation is x since it is highly unlikely that including the factor of \(10^{-32}\) will make any significant difference to the tree’s prediction. Algebraic simplification, however, would fail to recognize the \(x+\epsilon\) fragment as redundant because—in strict algebraic terms—it is not, and this has led researchers to employ approximate numerical methods. Many numerical simplification approaches have the over-riding disadvantage of requiring user-defined thresholds to gauge whether a candidate subtree has ‘no’ effect and can thus be pruned. In fact, the combined approach of Johnston et al. [11] requires the setting of six user-defined thresholds. In practice, it is difficult to see how to set these optimally other than by exhaustive grid search over the 6-dimensional parameter space; this grid search would need to be repeated anew for every new problem. Further, it is not clear how to gauge the optimal amount of tree simplification/performance degradation in order to terminate such a grid search.
In this paper we adopt an approach akin to numerical simplification [12]: we regard a subtree as redundant if its removal results in no statistically significant change in the output of the parent tree: our approach thus provides a principled method for accepting/rejecting a pruning proposal and avoids the need for user-defined thresholds. We explore the use of statistical permutation tests to determine if a selected subtree can be replaced with a constant of value equal to the mean of the subtree’s output over the data set; replacement by a constant node has also been followed by [12]. Other types of redundancy can be readily addressed by our scheme, but for the first report of this novel application of permutation testing to GP tree pruning, we restrict attention to exploring this cause of tree redundancy. Additionally—and unlike rule-based approaches—our method does not need tuning to the function set employed.
The key contribution over previous work on simplification is: Whether or not to accept a pruning proposal is judged statistically on the probability that a given pruning operation will change the output of the tree. This gives principled grounds for pruning decisions based on the probability of erroneous pruning. We thus avoid arbitrary, user-defined thresholds.
In particular, compared to earlier work on numerical simplification [13], the present approach:
-
1.
Removes the restriction of locality [13]. Previous work was restricted to considering the possible removal of single nodes, or the effect of redundancy one or two nodes higher in the tree [11]. The present approach, on the other hand, considers the possible redundancy of arbitrary subtrees of any size.
-
2.
Previous work [11, 13] employed user-defined thresholds; no principled method exists for setting these other than trial-and-error. (We argue that intuitions based on noise floor in the dataset [13] are fundamentally flawed—any threshold based on dataset noise variance that is ‘optimal’ at the leaves of a tree will be less and less appropriate as we approach the root due to the way noise variance propagates through compositions of functions.) The present approach based on probability, however, is principled and has the same interpretation at all tree depths.
-
3.
The work in [11, 13] uses the range of node’s output (i.e. max–min) to make the pruning decision. This approach is very sensitive to outliers in the dataset. The present approach, since it estimates probability by counting satisfied inequalities of the form \(a > b\), will not be catastrophically affected by an outlier, and is therefore robust.
Due to space constraints, we restrict this initial report to pruning the ‘best’ final tree produced by a conventional GP run rather than embedding tree simplification within the evolutionary dynamics. We thus critically re-examine the commonly held view that GP trees contain significant amounts of redundant material. Embedding permutation-based simplification within the evolutionary process is possible, but will require a much larger study to elucidate the various factors—we therefore defer that work to a future paper although we discuss possible approaches later in the paper. Further, since we consider here only pruning after evolution, the present work does not (currently) aim to control ‘bloat’ in the sense of avoiding unproductive code growth during evolution although that is obviously a future direction. In Sect. 1, we describe our GP tree pruning approach, and in Sect. 2 we outline the necessary background on permutation tests. The experimental methodology employed is described in Sect. 3 and results are presented in Sect. 4. We conclude the paper with a discussion and areas for future work in Sects. 5 and 6.
1 The pruning approach
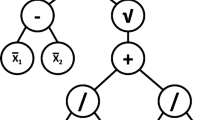
Considering the simple example tree representation in Fig. 1 which implements the quite general mapping \(y = f( {\mathbf {x}})\) where the vector \({\mathbf {x}} = (x_1 \, x_2 )^T\). This tree can be evaluated for a given \({\mathbf {x}}\) by recursively visiting each node in turn starting from the root node [21].
We consider the case of a subtree that produces the mapping \(g({\mathbf {x}})\) and denote \(c=\left\langle g({\mathbf {x}})\right\rangle\) where〈 〉denotes the expectation taken over a dataset. If replacing the given subtree by a constant node returning c does not produce a statistically significant change in the output of the parent tree then we can effect a simplification of the tree. We refer to this type of pruning as constant subtree (CST) pruning since the replaced subtree is effectively a constant.
In order to implement the constant subtree pruning strategy described in this work, the basic tree structure in Fig. 1 together with its recursive evaluation have to be modified. Firstly, we add an internal state variable to every node type. Thus: \(\text {NodeState} \in \{ \text {Untested, Testing, Failed, Pruned} \}\) where the different state values have the following interpretations:
-
‘Untested’ denotes that the subtree rooted at that node has not yet been considered for pruning.
-
‘Testing’ denotes that a node is currently in the process of being evaluated for pruning.
-
‘Failed’ indicates that the subtree rooted at this node has been considered for pruning, but this pruning proposal has been rejected.
-
‘Pruned’ indicates that a node and its subtree have previously been considered for pruning, and the pruning was judged to make no statistical difference to the tree output; in other words, the node and its subtree are redundant and can be replaced by the expectation of the subtree output over the dataset.
In order to implement the pruning approach proposed here, the tree evaluation function described above has to be modified to respect the node state. When the recursive evaluation of the tree encounters a node state of either ‘Testing’or ‘Pruned’ it immediately returns the (precomputed) mean value of the subtree; otherwise, the recursive evaluation continues conventionally.
The pruning process proceeds in the following sequence:
-
1.
Since the tree implements the mapping \(y_i = f({\mathbf {x_i}}) \quad \forall i \in [1 \ldots N]\), the response of the unpruned tree to each of the N records is cached in an indexed array \(D_u\), where the ‘u’ subscript denotes ‘unpruned’. This stage is performed to speed up subsequent permutation testing.
-
2.
All node states in the tree are initially set to ‘Untested’ denoting that at this stage none of the subtrees has been considered for pruning.
-
3.
-
(a)
The state of every (non-constant) node in the GP tree is set, one-at-a-time, to the ‘Testing’ state, and the tree evaluated over the N data records using a recursive tree evaluation procedure that respects node states. To facilitate rapid permutation testing, the responses of the (tentatively pruned) tree or each \({\mathbf {x}}\) value are cached in an array \(D_p\), where the ‘p’ subscript denotes pruned.
-
(b)
A permutation test—see Sect. 2—is carried out using the arrays \(D_u\) and \(D_p\) to explore the null hypothesis that the tentative pruning does not statistically change the behavior of the GP tree. If the null hypothesis is accepted, or the tentatively pruned tree produces a lower error, we can infer that the subtree rooted at the node whose state has been set to ‘Testing’ is redundant, and can be replaced with its mean value; its node state is then set to ‘Pruned’. On the other hand, if the permutation test implies that the tentatively pruned tree produces a statistically worse error than the unpruned tree this subtree cannot be pruned and the node state is set to ‘Failed’.
-
(a)
Full implementation details of the pruning process are described in [23].
Note there is a subtlety here in the interpretation of the permutation test. The outcome of the test is either to reject or accept the null hypothesis that the two subjects—the data in arrays \(D_u\) and \(D_p\)—do not differ. Rejection of the null hypothesis means that the original and modified trees are (statistically) different and so the subtree under consideration cannot be replaced with a constant node without changing the tree’s output. Similarly, acceptance of the null hypothesis means that the subtree in question may be replaced by a constant of a value equal to the average subtree output.
Returning to Fig. 1, the pruning process can be illustrated in the following way. Initially, all node states are set to ‘Untested’. First, the state of node ‘1’ is set to ‘Testing’ to explore the hypothesis that the whole tree can be replaced by a single constant equal to the average of the tree output over the dataset. If, say, this hypothesis is rejected by the permutation test then the node’s state is changed from ‘Testing’ \(\rightarrow\) ‘Failed’. The next hypothesis to be examined is to set state of ‘2’ to ‘Testing’ which explores the possibility that the subtree formed by nodes ‘2’, ‘3’and ‘4’ can be replaced by a constant with the value of the average output of ‘2’. If the ensuing permutation test rejects the hypothesis then the state of ‘2’ is set to ‘Failed’ and the procedure continues. If, on the other hand, the hypothesis that the subtree comprising nodes ‘2’,‘3’ and ‘4’ can be replaced by a single, constant node, then the state of ‘2’ is set to ‘Pruned’.
In practice, we examine the proposal to remove all possible (non-constant) nodes in the tree. In principle, we could examine a tree top-down and as soon as we identify a subtree that can be pruned, strictly there is no point in examining pruning proposals lower down in that subtree. In terms of implementation, however, the permutation testing procedure (Sect. 2), and in particular, its multiple comparison procedures, require that we know the total number of hypothesis tests before making a prune/no prune decision. Top-down pruning would thus be paradoxical. Nonetheless, the tree evaluation procedure after pruning does terminate recursive evaluation soon as it encounters a ‘Pruned’ subtree; we consequently do take advantage of the first pruning encountered in the recursive tree traversal thereby maximizing the degree of a tree’s simplification.
For the sake of statistical validity, conventional machine learning prescribes the use of three disjoint datasets: a training set, a validation set, and a test set—see [8, p.222], for example. The training set is used for parameter adjustment and yields the so-called substitution error that is usually a wildly optimistic estimate of generalization performance, and is of little significance beyond model training. Given some number of competing trained models, the validation set is used to select one model for adoption—formally, a model selection stage. Performance over the validation set is generally an optimistic estimate of the chosen model’s generalization error since the model has been selected based on its performance over the (finite) validation set. Finally, an estimate of the model’s generalization performance is obtained from the test set although since this too is finite, the estimate is uncertain but hopefully unbiased. In the context of tree pruning, we are performing a model selection procedure: that is, given a choice between two models—the original, as-evolved tree and the pruned tree, we accept a given pruning proposal if the two model responses are ‘identical’ since, by definition, the pruned model is simpler and therefore to be preferred. In summary, we employ the validation set for tree pruning since this is a model selection process.
2 Permutation testing
Permutation tests were originally devised by the English statistician Ronald Fisher in the 1930s as a means of illustrating hypothesis tests. Given two groups of subjects \({\mathscr {A}}\) and \({\mathscr {B}}\), both of size n, with two values of some statistic T, \(T({\mathscr {A}})\) and \(T({\mathscr {B}})\) computed over each group, respectively, and an observed difference \(\delta _{{\mathscr {A}},{\mathscr {B}}} = T({\mathscr {A}}) - T({\mathscr {B}})\) where \(\delta _{{\mathscr {A}},{\mathscr {B}}} \in \Delta _{{\mathscr {A}},{\mathscr {B}}}\). The null hypothesis \(H_0\) assumes that groups \({\mathscr {A}}\) and \({\mathscr {B}}\) are drawn from the same population so the expectation value of \(\delta _{{\mathscr {A}},{\mathscr {B}}}\), should be identically zero. If the null hypothesis is true then we are at liberty to randomly allocate the 2n data in \({\mathscr {A}} \cup {\mathscr {B}}\) to either one of two test groups, say, \(\mathscr {C}\) and \(\mathscr {D}\), allocating n data to each, and computing a new value of test statistic \(\delta _{\mathscr {C},\mathscr {D}}\). If we repeat this random allocation to \(\mathscr {C}\) or \(\mathscr {D}\) a large number of times, each time obtaining a different value of \(\delta _{\mathscr {C},\mathscr {D}}\), we can obtain a distribution of \(\Delta _{\mathscr {C},\mathscr {D}}\), the so-called permutation distribution. Under the null hypothesis \(\left\langle \delta _{C,D} \right\rangle = 0\).
By computing the probability that the observed difference \(\delta _{{\mathscr {A}},{\mathscr {B}}}\) could have been drawn from the permutation distribution, we have three potential outcomes for the permutation test:
-
1.
\({\mathscr {A}}\) and \({\mathscr {B}}\) are (statistically) identical and so the given pruning proposal can be accepted.
-
2.
The performance of group \({\mathscr {A}}\) is better than that of \({\mathscr {B}}\). If \({\mathscr {A}}\) is from the pruned tree we can accept the pruning proposal since improving the performance of the tree is (probably) beneficial.
-
3.
The performance of \({\mathscr {A}}\) is worse than \({\mathscr {B}}\); if again, \({\mathscr {A}}\) are the pruned responses then we wish to reject that pruning proposal.
Since we are concerned with rejecting a pruning proposal only if it produces a worse outcome, we adopt a one-sided hypothesis test. Permutation tests are described in greater detail in [4, 7, 16].
(We should at this point note a difference in terminology in the literature. Fisher’s original thought experiment to illustrate hypothesis testing involved assembling a permutation distribution with all n! exhaustive permutations of the data. For even modest values on n, of course, this exact approach becomes infeasible, and practitioners typically approximate the permutation distribution using resampling—as described above—leading to the alternative name of a randomization test. Here we adopt the commonly-used terminology of “permutation test” for the resampling procedure.)
In the context of GP tree pruning in a regression problem, we can consider the two groups of squared errors for each of the n data records in the validation set as the two groups \({\mathscr {A}}\) and \({\mathscr {B}}\). One is obtained from the original, as-evolved tree and the other with replacing a given subtree with a constant, as described in Sect. 1.
Two key technical points need to be considered at this point: firstly, whether pruning affects the generalization ability of the model. The procedure being implemented here is model selection. (It is for that reason we use the validation set for the permutation test rather than the training set or a test set—generalization error is estimated over a separate test set.) To select between two models—pruned and unpruned—we pose the question: does the unpruned tree exhibit the (statistically) same error over the validation set? If this question is answered in the affirmative then we prefer the the simpler tree according to Occam’s razor. In reality, this question only makes any sense with respect to the validation set. If more data were available then we could use them both to improve the training and to reduce the variance on the model selection decision. Consequently, questions about generalization should be unconnected to the pruning decisions. We hypothesize that accepting a pruning proposal on the basis of comparing validation set errors will have no systematic effect on the test (generalization) error. In essence, if we have an (obvious) redundancy of the form, say, \(y = f(x) + x - x\) then simplifying this to \(y = f(x)\) will not affect the generalization error of the model. Thus we conjecture that due to sampling effects pruning will sometimes reduce test error and sometimes increase it, but overall, will have no statistically significant effect; this point is addressed further in Sect. 4.3.
In terms of implementation, the quantities we are permuting are the two groups of n squared residuals obtained with and without a pruning proposal. Consequently, it is only necessary to calculate these once at the start of a subtree pruning process and cache them (in arrays \(D_u\) and \(D_p\)). The computational demands of a given permutation test are thus modest. Further, we are interested in the decision about whether pruning some given subtree results in (statistically) the same tree semantics as the original, as-evolved tree (\(D_u\)), and not the last pruned tree. Consequently, our ‘reference’ responses from the as-evolved, unpruned tree do not change during the sequence of pruning decisions for the whole tree.
The second technical issue concerns multiple comparison procedures (MCPs) [9]. In this work, we are computing multiple test statistics, and there is a well-known issue with such comparisons tending to increase the error rate over families of tests [9]. (We think it self-evident that the set of tests we employ do comprise a family [9].) The concept of MCPs is well-known to the GP community albeit in the guise of the post hoc corrections that usually follow Friedman tests of group homogeneity [6]. In hypothesis testing there are two sorts of error: Type I error, which occurs with probability \(\alpha\), is the situation where a null hypothesis is erroneously rejected. Complementary to this, a Type II error, which occurs with probability \(\beta\), is the mistaken rejection of the alternative hypothesis; the quantity \((1-\beta )\) is denoted the power of the test. When \(\alpha\) increases, \(\beta\) decreases, and vice versa although the exact functional form is hard to specify in general. In the context of the present work, a Type I error will lead to the rejection of a (perfectly good) pruning proposal and is benign (except that a possible opportunity to simplify the tree has been missed). A Type II error, on the other hand, leads to accepting a pruning proposal that should really have been rejected. Consequently, controlling Type II error is of greater importance in this work. Most multiple comparison procedures, however, have been focused on controlling Type I error although the false discovery rate (FDR) procedure of Benjamini and Hochberg [1] has been shown to maintain test power and is therefore appropriate here. We have therefore adopted the FDR procedure here.
3 Experimental methodology
We have employed a fairly standard generational GP search in this work [21]. The parameters of the algorithm are summarized in Table 1. We have used 10% elitism and therefore generated the remainder of the child population by always applying crossover and mutation to ensure population diversity. If a breeding operation generated a tree larger than the pre-specified hard node count limit, one of the parent trees was randomly selected for copying into the child population [21].
We have employed a set of ten univariate regression test functions that have previously been used in the GP literature—see Table 2. The first four of these functions are, in principle, representable exactly with the internal nodes used in the GP. The remaining functions require appropriate approximation. We have used training sets of 20 data randomly sampled over the domain, and validation sets of the same size; the test sets comprised 1000 data in order to obtain reliable estimates of generalization error. The rather small size of 20 training/validation data was quite deliberate and is related to the challenge presented by various test functions for GP, which has received some attention [17]. In particular, the difficulty associated with learning high-dimensional problems stems from the exponentially-decreasing density of data with increasing problem dimensionality—the so-called ‘curse of dimensionality’. At the same time, we wanted to focus on univariate problems to facilitate more straightforward analysis of the pruned subtrees (although, in the event, this proved optimistic). Hence the choice of 20 training data so as to pose a set of fairly ill-conditioned and therefore challenging learning problems; a 50:50 split between training and validation sets is commonplace in machine learning practice leading to a choice of validation sets of 20 data.
We have standardized on the range of hard node limits of \([16 \ldots 256]\), which corresponds, under the assumption of all binary internal nodes, to tree depths of \([4 \ldots 8]\), a range typically employed to solve problems such as the test functions used here.
Throughout this work, we have use the commonly-accepted significance level of \(5\%\) for permutation testing. In other words, a 1-in-20 chance that the observed statistic could have been obtained fortuitously. We have used 10,000 samples for the permutation testing, a figure arrived at simply by increasing the number of trials from a low starting point until the estimators stabilized. Both the 5% acceptance probability and the number of permutation test samples strictly comprise parameters for the algorithm, but the former has the advantage of being unambiguously interpretable (as opposed to an arbitrary threshold). Although we have not employed it here, Gandy [5] has shown it is possible to terminate the permutation testing as soon as the uncertainty on the computed p value has fallen below a limit.
4 Results
After evolving a final population of GP regression trees, we selected the individual with the smallest training error for subsequent pruning. We have applied our permutation-test-based pruning procedure to establish the influence of these statistical modifications. Further, we have explored the effect of pruning on the generalization errors in Sect. 4.3.
4.1 Pruned tree sizes
The typical distributions of tree node counts for the French curve test function for a range of hard node count limits is shown in Fig. 2; these have been accumulated over 1000 repetitions, each with independent initial populations. (All results have incorporated the Benjamini & Hochberg multiple comparison procedures.) In fact, the corresponding plots for all the test functions look remarkably similar.Footnote 1
Figure 2 shows the node counts for the final evolved individuals with the smallest training errors before pruning. We only compare distributions over trees for which subsequent pruning was possible, and ignored (the small minority of) trees were no pruning occurred. It is clear from this figure that for a given hard node count, the GP evolution tended to produce trees almost exactly this size and with small interquartile ranges although some smaller trees were generated as evidenced by the lower whiskers on the box plots.
The node count distributions after pruning are shown in Fig. 3. There appears to be a roughly 20% consistent reduction in median tree size (independent of test function) although comparing with the corresponding boxplots before pruning, there is a noticeable increase in the interquartile ranges. From the upper whiskers of the box plots, it is clear that in an appreciable number of cases the trees have been reduced in size only marginally.
Figure 4 shows the typical relationships between unpruned and pruned individuals for the French curve test function and a hard node count limit of 128. Points on the two parallel axes show the unpruned tree sizes (left) and pruned tree sizes (right) for the same individuals before and after pruning. For comparison, the two distributions of individuals are shown as boxplots for unpruned (left) and pruned (right) populations. It is clear from this figure that unpruned individuals with an interquartile range of \([123 \ldots 127]\) are being pruned to a wide range of tree sizes with a corresponding interquartile range of \([88 \ldots 105]\). The median size is reduced from 126 to 97. Although some small unpruned individuals are being reduced by only modest extents, there are also large individuals (\(\sim \,110\)–128 nodes) being pruned down to between 60 and 80 nodes. A few are being pruned to \(\sim \,40\) nodes.
4.2 Distributions of pruned tree sizes
The results in the previous section are for trees to which all possible pruning proposals have been applied, and are therefore reduced to their minimum size. We have, however, also carefully analyzed the individually-accepted pruning proposals. Figure 5 shows the typical distributions of the sizes of pruned subtrees for the French curve functions; again there is comparatively little variation with test function/hard node count limit. The noteworthy features of these distributions are (i) their small interquartile ranges, and (ii) most of the pruned trees tend to be rather small in size although a few subtrees in excess of one hundred nodes can also be removed by pruning. The median value of pruned tree size is three independent of test function and node count limit. It thus seems highly likely that the most commonly pruned tree comprises a binary node and either two terminals or two constants.
We have examined the distributions of pruned tree sizes in detail paying particular attention to accepted pruning proposals of three nodes, and this analysis is shown in Table 3. (Yet again, there is little variation with test function.)
The row “# pruning events” shows the absolute number of successful pruning events over 1000 repetitions of tree evolution—this unsurprisingly increases with increasing node count limit as larger trees offer more opportunities for pruning. Of these pruning events, the percentage involving 3-node trees is indicated by “% 3-node trees”—it is clear that this covers around 40-50% of the individual pruning events. Within these 40-50% of overall 3-node tree prunings, the table also shows the percentages that are a binary operations with two constant children (“% \(\text {constant} \circledast \text {constant}\)”), the percentage of \((x - x)\) operations (“% \((x - x)\)”) together with a summary of the 3-node prunings that are algebraic simplifications (“% 3-node algebraic”). Thus, in this particular case, between 93.94% and 82.39% of the 3-node prunings are algebraic simplifications. A small percentage of 3-node prunings are other binary-rooted subtrees (“% other binary”) and these comprise subtrees implementing ‘\(x \circledast \text {const}\)’ (or ‘\(\text {const} \circledast x\)’); only a very small percentage of these ‘other binary’ operations are ‘\(x-0 \rightarrow x\)’ or \(x \times 1 \rightarrow x\) simplifications. Finally, around 5–10% (across all functions) of pruned 3-node trees are algebraic simplifications of the form \(-(-x)\) or \(-(-\text {constant})\) (‘% 3-node unary’), that is, a subtree comprising two cancelling unary minus operations and a terminal.
From the above results (and others [23]), it thus seems clear that around \(\sim \,80\)–95% of the 3-node prunings represent algebraic simplifications being carried out—by definition—at the peripheries of trees. It is important to re-emphasise, however, that these 3-node simplifications, however, account for only around half of the total number of pruning events. Some of the pruned trees larger than three nodes may well be producing algebraic simplification, but this is difficult to verify due to the increasing number of ways an equivalent expression may be written. Some more insight, however, may be gained by examining what fraction of the permutation tests returned a precisely zero probability of rejecting the null hypothesis. We infer that such a result can only be delivered when the two trees responses—with vs. without pruning—are absolutely identical implying that the pruning being considered represents an algebraic simplification. These percentages are shown in Table 4 for each test function and hard node limit, and for 3-node trees as well as pruned trees larger than three nodes. It is clear that, in general, at least the high nineties of percent of pruning probabilities are zero implying that these represent algebraic simplification.Footnote 2 A slightly smaller percentage of trees larger than three nodes returns zero probability than the corresponding figure for 3-node trees although this is reasonable given that there is greater scope for larger trees to be approximately rather than algebraically equivalent.
4.3 Effect of pruning on the generalization error
If pruning makes no difference to the model selection decision (i.e. validation set error) other than producing a smaller tree, we conjectured that pruning can have no effect on the average generalization error of the tree. We have explored this hypothesis by generating a (third) test set [8, p.222] of 1000 data independent of both the training and validation sets to estimate the generalization errors of 1000 trees generated from independent GP runs. We return here to comparing trees both before pruning, and after all possible pruning proposals have been applied and the tree reduced to its minimum overall size. We removed from this experiment the few % of trees that remained unpruned since we were interested only in the effects of pruning, not its frequency of occurrence. If pruning does not affect generalization performance—which is, by definition, the average error over test sets—then by chance we would expect exactly half the (pruned) trees to exhibit an improved test error after pruning and half to have a higher test error after pruning.
We have explored with a series of statistical tests the hypothesis that pruning (on average) either improves or degrades the generalization error; the results are summarized in Table 5 for a representative selection of test functions. For each of the 1000 pruned trees examined, the generalization error was either unchanged, increased by pruning or decreased by it. Between 58 and 100% of the generalization errors were unchanged by pruning and we followed the usual statistical practice of distributing these zero before-and-after differences equally between the counts for improved and degraded test errors; we explored the one-sided hypothesis for whichever count (improvement/degradation) was larger. Which test has been applied is shown in the table with either a down-arrow (\(\downarrow\)) for a reduction (improvement) in test error , or an up-arrow (\(\uparrow\)) for an increase (degradation).
From Table 5 for trees trained with 20 data (suffix of “-20”), it is clear that most of the null hypotheses need to be accepted (= ‘no change’ in test error) although for a hard node count limit of 256, the generalization error statistically worsens. (Complete data can be found in [23] from which a less clear trend emerges: mostly, test error is unchanged, sometimes it improves, sometimes it degrades.) This picture of unclear effects on test error has also been reported in [30, 31].
Training the GP trees with 100 data but retaining a validation set size (that was used for pruning) of 20 data, however, does produce a consistent pattern. The trees in this series of experiments should thus be better trained before pruning. The results of this second series of experiments are shown in Table 5 (suffix of “-100”) where all hypothesis tests are against improvements in test error. That is, tree prunings always yielded net reductions in test error. This can be understood since improved training means that the GP function better approximates the target function; pruning here is always referenced to the performance of the as-evolved tree and if this is deficiently trained then pruning will find simpler approximations to this deficient approximation. It is also apparent from this table that statistically-significant reductions tend to be greater for larger tree node limits. This is sensible since larger node limits tend to produce larger trees that are more likely to contain redundant subtrees.
5 Discussion and future work
From the results presented in this paper it is apparent that the proposed permutation-based pruning procedure is effective in reducing median tree sizes by about 20% independent of test function and hard node count limit. Whereas the distributions of as-evolved tree sizes clustered near to the hard node count limit, after pruning the variability of the tree sizes increased noticeably. It should also be noted that some (large) trees were pruned down to quite small sizes.
The results from the Salustowicz function stand alone across a number of comparisons. We have noted above the probable challenge of reliably learning a function with such a large number of extrema from just 20 data; Vladislavleva et al. [28] have previously remarked that this function is challenging for GP. Some of the trees attempting to approximate the Salustowicz function have been pruned down to single nodes implying that GP could find no better approximation than a constant, presumably close to the mean value of the function. Clearly, the results from the Salustowicz function underline that the the interplay between pruning and the adequacy of training warrants further research.
As regards the composition of the subtrees being pruned, around half are 3-node, binary-rooted trees having the forms: constant \(\circledast\) constant, \(x - x\) or \(x \times 1\), where ‘\(\circledast\)’ is an arbitrary binary operation. These are clearly being pruned from the peripheries of trees. Within the context of the statistically-founded method presented here, a permutation test p value of identically zero implies (though, of course, does not prove) that a pruned subtree removal represents an algebraic simplification as opposed to an approximate simplification. (That said, it is difficult to think of another plausible explanation for zero probability values.) The inference overall is that the overwhelming majority (\(\gtrsim \,\)95%) of accepted prunings are algebraic simplifications. Clearly a corollary is that only few percent of prunings are approximate simplifications. This was an unexpected finding since it was originally anticipated that a far higher percentage of approximate prunings would be observed.
The implications for the change in generalization error caused by pruning are interesting. A majority (\(\gtrsim \,\)58%) but by no means all prunings produced no change in generalization performance for individual trees. If \(\gtrsim \,\)95% of all prunings are algebraic simplifications—which, by definition, cannot change the approximating function and therefore the generalization—then those changes in generalization that do occur must be caused by a relatively small number of pruning events. Although we have shown that pruning either leaves generalization unchanged or reduces it on average, assuming the tree is sufficiently well trained, instances where test error is reduced are obviously counterbalanced by instances where the test error increases. In this situation, approximate prunings might be viewed as risky due to their potentially adverse effects, and so a more conservative approach would be to only accept prunings with zero p values, that is, prunings that can be inferred to be algebraic simplifications. (Notwithstanding, the original motivation of the work to explore approximate simplifications has allowed us to quantify this effect.)
Although pruning mostly leaves test error unchanged and occasionally degrades it, there are clearly many occasions when pruning actually improves the test error. A similar phenomenon has been observed in the induction of conventional decision trees (DTs) where, typically, a DT is trained to the point of overfitting and then heuristically pruned to improve generalization [22]; this phenomenon can be easily interpreted in terms of advantageously shifting the balance between goodness-of-fit and model complexity [8]. Pruning obviously reducing the latter quantity.
One aspect of this work does require justification, and was indeed raised by one of the anonymous reviewers of this paper: the absence of a direct comparison with previous approaches to approximate simplification, such as [13]. To be of any value, any comparison has to a be a fair comparison. Since, as pointed out in the introduction, a fundamental shortcoming of previous work is its reliance on user-defined thresholds for which there are no principled selection methods, the question arises as to how to select a ‘fair’ threshold for comparison? Selecting such an arbitrary value is open to all sorts of potential abuses with investigator bias—for example, it would be possible to adopt some value that purports to show the spectacular superiority of the present method, but such a comparison would be barely worthy of the name. Making comparison across a range of threshold values is similarly unsatisfactory in that progressively lowering the decision threshold will increase the degree of pruning but will also degrade the test error as increasing numbers of increasingly inappropriate prunings were accepted. How to judge which is the ‘correct’ degree of tree simplification? In the light of these difficulties, we have taken the deliberate decision to omit controversy-laden attempts at comparison with previous work.
Although this paper reports the development of a principled, statistically-founded method based on repeated sampling, incorporation of the necessary multiple comparison procedures has meant we need to explore all potential prunings. The computational complexity for a tree of depth d can be upper-bounded by considering a tree comprised only binary nodes. At each level i in the tree we have \(2^i\) subtrees so the total number of pruning proposals that need to be considered is:
It would, however, be misleading to to infer that this is a computationally intractable algorithm. Tree depth d is typically small (\(\le 8-10\)), and it is well-known that many NP-hard problems are eminently solvable for small problem sizes. Pruning the single, best-trained individual from the evolved population increased the CPU time by around 25% in the present work, a fairly modest increase although this could be reduced by employing the ‘early jump out’ approach in [5]. Extending this approach directly to pruning trees during evolution will clearly result in a significant increase in runtime. It would, nonetheless, be interesting to see how approximate tree simplification affects the evolutionary dynamics as a one-off experiment both for the single-objective GP formulation considered here as well as multi-objective GP that incorporates syntactic bloat control in a different way. It is moot, however, whether the inevitably large increase in computing time would impact workaday GP practice. We return to this theme in the following paragraph.
Overall, the scope for reducing tree size appears to stem almost exclusively from algebraic simplification; scope for approximate simplification appears comparatively rare and carries the risk of degrading the model generalization but also the possible benefit of improving it. This paper has quantified the scope for approximate simplification of GP trees using a principled, statistically-founded method that avoids the need for arbitrary, user-tuned decision thresholds. The rather surprising conclusion is that \(\ge\)95% of the possible tree simplifications are purely algebraic, the practical implications of which are profound. This suggests that almost all the benefits of tree size reduction can be achieved by algebraic simplification while avoiding the risks of degrading the generalization performance that approximate simplifications bring. However, rather than suggesting the use of rule-based simplifications of tree syntax [30, 31] that need to be handcrafted to the function set, and, like all complex rule sets, are challenging to construct, a simpler, semantic-based approach based on the present work suggests itself. Algebraic simplification for a tree of arbitrary complexity can be inferred by comparing the elements of the two cached arrays of tree responses \(D_u\) and \(D_p\) (see Sect. 1). If \(D_u[i] \approxeq D_p[i] \ \; \forall i \in [1 \ldots N]\) where N is the size of the data set and “\(\approxeq\)” denotes equality within floating-point rounding error, we can infer algebraic equivalence and prune the candidate subtree without changing the tree’s semantics. Such as scheme retains the benefits of the permutation test but without the need for repeated sampling leading to a large saving in computing time. Applying this non-sampling approach to tree simplification both during evolution and on members of the final evolved population is an area of future work.
Although ‘bloat’ has long been recognized as an issue in genetic programming, its handling has in the past been rather informal [27]. The present work offers a possible route to a more rigorous definition in that it identifies subtrees that make no significant contribution to the program’s output, serving only to increase the size of the tree. We have presented a method of judging (to within some statistical bound) whether or not a tree fragment is redundant. Although we have been concerned here exclusively with post hoc tree pruning, it is clearly an area of future work to focus explicitly on bloat.
Although we have considered only unary and binary nodes here, extension to ternary (if-then-else) nodes [21] is straightforward. Typically, the first subtree is used to evaluate the conditional predicate; if this predicate evaluates to ‘true’, then the value of the second subtree is returned, otherwise the value of the third subtree is returned to the node’s parent. It is straightforward to extend the above pruning strategies to evaluate the hypotheses that the ternary node could be replaced by either the second (‘true’) subtree or the third (‘false’) subtree implying that the conditional predicate is (effectively) a constant value and that the branching structure is redundant.
Clearly future work needs to examine more complex regression functions, such as those suggested in [17]; these more ‘complex’ mappings should produce more complex trees that may change the nature of pruning. Although the work reported in this paper is restricted to regression problems, extension to classification and indeed time series is straightforward, and will be addressed in forthcoming research.
Finally, and in terms of future work on simplification, consider the expression comprising two binary nodes: \(z = (x+y) - y\), which, of course, algebraically simplifies trivially to \(z = x\). This expression cannot, in general, be simplified by setting any of the variables to a constant. (The reader is invited to draw this expression as a tree and consider the two outcomes—pruned and unpruned—if the subtree rooted at the ‘−’ node is replaced by the average over, say, two data records \((x_1, y_1)\) and \((x_2, y_2)\).) Reductions of subtrees such as this are likely to remain a challenging task, especially if x, y are not terminal quantities but are themselves computed by (possibly large) subtrees and where y is computed by two subtrees of markedly different morphologies. Even constructing simplification rules for this case remains challenging; to account for the ‘canceling’ factor—here y—lying lower and lower in the left hand subtree requires an exponentially increasing number of rules. There thus seems a large amount of work remaining to simplify GP trees to their truly minimal form.
6 Conclusions
In this paper, we have presented a novel approach based on statistical permutation tests for pruning redundant subtrees from genetic programming (GP) trees. This has the advantage of being simple to implement while not requiring the setting of arbitrary, user-defined thresholds.
We have observed that over a range of ten regression problems, median tree sizes are reduced by around 20%, largely independent of regression function and the hard node count limit used to restrict tree bloat. Although some large subtrees (over a hundred nodes) are removed, the median pruned subtree comprises three nodes and overwhelmingly takes the form of an exact algebraic simplification. That is, either a binary operation on two constants, a subtraction operation on two variable nodes, a multiplication of a variable by unity, or two consecutive unary minus operators and a terminal node.
The basis of our statistically-based pruning technique is that a given subtree can be replaced with a constant if this substitution results in no statistical change to the behavior of the parent tree. This has allowed us to examine approximate redundancies where replacing a subtree with a constant produces some change, but that that change is not statistically significant. In the eventuality, we infer that \(\gtrsim \,\)95% of the pruned subtrees are the result of algebraic simplifications since this fraction of hypothesis tests yielded precisely zero p values. These observations suggest the scope for reducing the complexity of GP trees is overwhelmingly limited to algebraic simplification and that instances of removing approximate equivalences are comparatively rare.
The further implication of the rarity of approximate simplification prunings is that most pruning events do not change the generalization error of the parent tree. The small number of approximate prunings that do occur, however, can have effects—both positive and negative—on generalization.
References
Benjamini Y, Hochberg Y (1995) Controlling the false discovery rate: a practical and powerful approach to multiple testing. J R Stat Soc B Methodol 57(1):289–300
Blickle T, Thiele L (1994) Genetic programming and redundancy. In: Workshop on genetic algorithms within the framework of evolutionary computation, Saarbrücken, Germany, pp 33–38
Dick G (2017) Sensitivity-like analysis for feature selection in genetic programming. In: Genetic and evolutionary computation conference (GECCO 2017), Berlin, Germany, pp 401–408. https://doi.org/10.1145/3071178.3071338
Ernst MD (2004) Permutation methods: a basis for exact inference. Stat Sci 19(4):676–685. https://doi.org/10.1214/088342304000000396
Gandy A (2009) Sequential implementation of Monte Carlo tests with uniformly bounded resampling risk. J Am Stat Assoc 104(488):1504–1511. https://doi.org/10.1198/jasa.2009.tm08368
García S, Fernández A, Luengo J, Herrera F (2010) Advanced nonparametric tests for multiple comparisons in the design of experiments in computational intelligence and data mining: experimental analysis of power. Inf Sci 180(10):2044–2064. https://doi.org/10.1016/j.ins.2009.12.010
Good PI (1994) Permutation tests: a practical guide to resampling methods for testing hypotheses. Springer, New York
Hastie T, Tibshirani R, Friedman J (2009) The elements of statistical learning: data mining, inference, and prediction, 2nd edn. Springer, New York
Hochberg Y, Tamhane AC (1987) Multiple comparison procedures. Wiley, New York
Jackson D (2010) The identification and exploitation of dormancy in genetic programming. Genet Program Evolvable Mach 11(1):89–121. https://doi.org/10.1007/s10710-009-9086-1
Johnston M, Liddle T, Zhang M (2010) A relaxed approach to simplification in genetic programming. In: 13th European conference on genetic programming (EuroGP’10), Istanbul, Turkey, pp 110–121. https://doi.org/10.1007/978-3-642-12148-7_10
Kinzett D, Johnston M, Zhang M (2009) Numerical simplification for bloat control and analysis of building blocks in genetic programming. Evol Intell 2(4):151–168. https://doi.org/10.1007/s12065-009-0029-9
Kinzett D, Zhang M, Johnston M (2010) Investigation of simplification threshold and noise level of input data in numerical simplification of genetic programs. In: IEEE congress on evolutionary computation, (CEC2010), Barcelona, Spain, pp 1–8. https://doi.org/10.1109/CEC.2010.5586181
Koza JR (1992) Genetic programming: on the programming of computers by means of natural selection. MIT Press, Cambridge, MA
Langdon WB (2017) Long-term evolution of genetic programming populations. In: Genetic and evolutionary computation conference companion, Berlin, Germany, pp 235–236. https://doi.org/10.1145/3067695.3075965
Manly BFJ (1997) Randomization, bootstrap and Monte Carlo methods in biology, 2nd edn. Chapman & Hall, London
McDermott J, White DR, Luke S, Manzoni L, Castelli M, Vanneschi L, Jaskowski W, Krawiec K, Harper R, De Jong K, O’Reilly UM (2012) Genetic programming needs better benchmarks. In: Genetic and evolutionary computation conference (GECCO 2012). Philadelphia, PA, pp 791–798. https://doi.org/10.1145/2330163.2330273
Naoki M, McKay B, Hoai NX, Essam D, Takeuchi S (2009) A new method for simplifying algebraic expressions in genetic programming called equivalent decision simplification. In: 10th International work-conference on artificial neural networks, (IWANN) workshops on distributed computing, artificial intelligence, bioinformatics, soft computing, and ambient assisted living, Salamanca, Spain, pp 171–178. https://doi.org/10.1007/978-3-642-02481-824
Ni J, Drieberg RH, Rockett PI (2013) The use of an analytic quotient operator in genetic programming. IEEE Trans Evol Comput 17(1):146–152. https://doi.org/10.1109/TEVC.2012.2195319
Nordin P, Francone F, Banzhaf W (1995) Explicitly defined introns and destructive crossover in genetic programming. In: Workshop on genetic programming: from theory to real-world applications, Tahoe City, CA, pp 6–22
Poli R, Langdon WB, McPhee NF (2008) A field guide to genetic programming. Published via http://lulu.com and freely available at http://www.gp-field-guide.org.uk. http://dces.essex.ac.uk/staff/rpoli/gp-field-guide/A_Field_Guide_to_Genetic_Programming.pdf. Accessed 14 Sept 2019
Quinlan JR (1993) C4.5: programs for machine learning. Morgan Kaufmann, San Mateo, CA
Rockett P (2018) Pruning of genetic programming trees using permutation tests. Technical report, University of Sheffield
Salustowicz R, Schmidhuber J (1997) Probabilistic incremental program evolution. Evol Comput 5(2):123–141. https://doi.org/10.1162/evco.1997.5.2.123
Song A, Chen D, Zhang M (2009) Bloat control in genetic programming by evaluating contribution of nodes. In: Genetic and evolutionary computation conference (GECCO 2009), Montreal, Canada, pp 1893–1894. https://doi.org/10.1145/1569901.1570221
Uy NQ, Hoai NX, O’Neill M, McKay R, Galván-López E (2011) Semantically-based crossover in genetic programming: application to real-valued symbolic regression. Genet Program Evolvable Methodol 12(2):91–119. https://doi.org/10.1007/s10710-010-9121-2
Vanneschi L, Castelli M, Silva S (2010) Measuring bloat, overfitting and functional complexity in genetic programming. In: Genetic and evolutionary computation conference (GECCO ’10), Portland, OR, pp 877–884. https://doi.org/10.1145/1830483.1830643
Vladislavleva EJ, Smits GF, den Hertog D (2009) Order of nonlinearity as a complexity measure for models generated by symbolic regression via Pareto genetic programming. IEEE Trans. Evol Comput 13(2):333–349. https://doi.org/10.1109/tevc.2008.926486
Wahba G, Wold S (1975) A completely automatic French curve: fitting spline functions by cross validation. Commun Stat 4(1):1–17. https://doi.org/10.1080/03610927508827223
Wong P, Zhang M (2006) Algebraic simplification of GP programs during evolution. In: Genetic and evolutionary computation conference (GECCO 2006), Seattle, WA, pp 927–934. https://doi.org/10.1145/1143997.1144156
Zhang M, Wong P, Qian D (2006) Online program simplification in genetic programming. In: 6th international conference on simulated evolution and learning (SEAL 2006), Hefei, China, pp 592–600. https://doi.org/10.1007/11903697_75
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Rockett, P. Pruning of genetic programming trees using permutation tests. Evol. Intel. 13, 649–661 (2020). https://doi.org/10.1007/s12065-020-00379-8
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12065-020-00379-8