Introduction

The developed world is going through a major demographic transition. Simultaneously, two processes can be observed. Firstly, we are experiencing slowing population growth. Secondly, in many countries the age structure of the population is changing. In order to describe these changes, the term new demographic regime has entered the discussion on the demographic situation in many countries (see for example Macura et al. 2005; Kotowska and Jóźwiak 2012). As for the European Union (EU) countries and, in fact, most of the OECD countries, this term refers to the simple fact that fertility rates in their populations are permanently lower than 2.1, which is below the simple replacement rate of generations. However, to understand the new demographic regime, one has to look at the whole process. Not only there are less children being born. Societies are also facing a change in relational and reproductive patterns. This change is often referred to as the second demographic transition. Among its most important characteristics, one can mention secularisation, changes in the character of marriage, pluralisation of family forms, and conflict between economic activity and motherhood. This conflict results not only in lower fertility rates, but also in postponing the decision to procreate, which increases the mean age at first birth. Furthermore, readiness to create traditional families is reduced – the mean age at first marriage is increasing, while informal relationships are gaining in popularity. Moreover, divorces rates and prevalence of patchwork families are increasing.

In the long term, these developments lead to strong changes in the age structure of populations as they change relations between the sizes of age groups. For example, in most European countries acceleration of population ageing will soon be concurrent with the decline in the working-age population, which means ageing of the labour force (Kotowska et al. 2013). In addition, the European Commission (2015) confirmed that Europe will soon be a continent with a significant reduction in the working-age population.

On the other hand, many advanced economies are nowadays facing a very low inflation rate. In recent years, the opinion that low levels of inflation may be linked with changing demographic population structures has become more popular in the public debate (see for example Shirakawa 2011a, b, 2012, 2013; Bullard et al. 2012). Therefore, a larger proportion of the elderly in advanced economies may make it more difficult to escape the low inflation trap. If there really is a link between demography and inflation, it may also have significant implications for the conduct of monetary policy. It would mean that this component of inflation is forecastable and probably could be taken into account when conducting monetary policy.

Many advanced economies are already facing or will face demographic change in the near future. Therefore, the question of the influence of a population’s age structure on inflation is gaining importance. The aim of this paper is to check whether inflation might be linked to the age structure of a population. It is analysed whether one can distinguish between the effects on inflation caused by two different dependent groups, namely changes in the proportions of young (aged 0–15) and elderly (aged 65 and over) in a population, especially if the rise in the old-age dependency ratio is correlated with a lower inflation rate.

The remainder of this paper is organised as follows: In the second section the literature that analyses this relationship and measures the impact of demography on inflation is reviewed and discussed. The third section describes the data and the methodology used in the empirical analysis. Finally, the fourth section investigates empirically the link between inflation and demography in selected economies, and concludes with a summary of the findings and recommendations for the future.

Literature Review

According to the author’s best knowledge, in the literature there is still little evidence on the impact of population ageing on inflation. Moreover, the few empirical studies that have been devoted to this topic remain inconclusive on the impact of demographic changes on inflation. Most publications in this field analyse the impact of demographics on such macroeconomic variables as economic growth or public finances, questioning their sustainability in a greyer world. For example, Bloom and Canning (2006) state that a large number of people outside the productive age in relation to the number of people in working age can reduce the pace of economic growth. At the same time, the authors note that in an economy where a greater proportion of the population is of working age, economic growth may accelerate.

Nevertheless, there are some studies that suggest the existence of a link between inflation and the age-structure of a population. This link was repeatedly mentioned by Shirakawa (2011a, b, 2012, 2013). The former Governor of the Bank of Japan stated that an ageing population could lead to an increase in deflationary pressures, primarily owing to expectations of a slowdown in economic growth. In addition, it may cause a reduction in consumer demand and investment. Looking at the publications on inflation and demography, two contradictory streams of research can be distinguished, as follows:

The more popular and traditional view emerges from the life-cycle hypothesis. As the median age of a population increases, more households finance their consumption from accumulated savings and do not directly produce added value. Therefore, the discrepancy between aggregate demand and output in the economy rises and demand-driven inflationary pressure appears. Simultaneously, as the labour supply shrinks, wages are pushed up, which increases inflation through the cost channel.

According to this theory, using data from the United States McMillan and Baesel (1990) predicted the moderation of inflation in the 1990s and confirmed the forecasting power of demographics for low-frequency inflation. They showed the positive inflationary impact coming from the dependents. Lindh and Malmberg (2000) using a panel model described the impact of demographics on the existence of low-frequency inflation. They estimated the relation between inflation and age structure on annual OECD data for the period 1960–1994 for 20 countries. According to their results, an increase in the proportion of net savers in a population dampens inflation, whereas retirees, especially younger ones, fan inflation as they start consuming out of accumulated pension claims. In line with their results, Yoon et al. (2014) conducted a panel data analysis to prove if population ageing has an economically and statistically significant impact on key macroeconomic variables. They found that in the long-run dependent cohorts appear to have positive inflationary pressures. Societies with larger dependent age groups and smaller working age populations face a statistically significant decline in hours worked, real rates of interest, savings and investments, and higher inflation.

More recently, Juselius and Takáts (2015), through a panel data analysis of 22 advanced economies over the 1955–2010 period, also suggest that population ageing could lead to increased inflationary pressures. Their estimates show that demography accounts for a third of the variation in inflation in the analysed period. They found a stable and significant relationship between the age structure of a population and low-frequency inflation. In their subsequent work, Juselius and Takáts (2016) confirmed that the age-structure of population is a systematic driver of inflation. They found a stable and significant correlation between demography and low-frequency inflation. Dependents are more inflationary than the working age population. According to their research, in the US this age-structure effect accounts for about 6.5 percentage points of deflation between 1975 and 2016.

Recently, new views appeared in the literature on the link between low inflation and ageing. In contrary to the works discussed above, this outlook concentrates on demand-side effects of population ageing, showing its deflationary impact. In an ageing population, changing consumption preferences lead to reduced aggregated demand and lower inflation. Analysing lifecycle consumption and saving patterns (see for example Ando and Modigliani 1963) suggests that net consumer cohorts (dependents) drive up the real equilibrium interest rate. Net savers, on the contrary, reduce it. This trend was analysed by Anderson et al. (2014), who by using the IMF GIMF Model find deflationary pressures from ageing, stemming mainly from declining GDP growth and falling land prices. Furthermore, empirical research conducted for Germany by Faik (2012) and for a sample of OECD countries by Gajewski (2015) show that demographic ageing exerts downward pressure on prices.

Bullard et al. (2012) indicate that a greater proportion of older people can cause the society to favour lower inflation because of its redistributive effects. They argue that central banks’ monetary policy decisions are influenced by the inflationary preferences of dominant voter groups. Therefore, when the elderly are the dominant group in a society, their tendency to prefer lower inflation rates may lead to the appearance of deflationary pressures. This may contribute to low rates of inflation or even deflation.

Another point of view considers that it is not ageing per se that causes deflationary or inflationary pressures. According to Katagiri et al. (2014), the effects of ageing may depend on its causes. In their paper, they state that ageing is deflationary when caused by an increase in longevity but it is inflationary when caused by a decline in birth rate. Using an OLG model, they prove that over the past 40 years ageing caused yearly deflation of about 0.6 percentage points in Japan. Furthermore, they showed that the direction in which population ageing affects the inflation rate depends on the roots of this process. They argue that ageing can be more deflationary when caused by increased life expectancy. Population ageing stemming from a decline in the birth rate generates inflation by shrinking the tax base and raising fiscal expenditure. These findings reveal that the effects of population ageing on general prices depend on the cause of the ageing. However, this hypothesis has not yet been further researched.

Data and Methodology

In this study the largest possible available sample of OECD countries is included. The sample covers 32 economies: Australia, Austria, Belgium, Canada, Chile, Czech Republic, Denmark, Estonia, Finland, Germany, Greece, Hungary, Iceland, Ireland, Italy, Japan, Korea, Latvia, Mexico, The Netherlands, New Zealand, Norway, Poland, Portugal, Slovak Republic, Slovenia, Spain, Sweden, Switzerland, Turkey, the United Kingdom, and the United States.

The reasons for excluding some of the countries from the sample were as follows: Luxembourg was excluded because the data concerning GDP are not very representative as a control variable for measuring relations between inflation and demography, as most of the Luxembourg labour force does not live in the country. As for other countries, the available data was insufficient to include them in the panel. In terms of time coverage, the sample is limited to 1971–2015. However, for some countries, especially from Eastern Europe, data before 1989 is not fully covered.

To show the age structure of the population, we use three different variables. First, the dependency ratio (denoted as depi, j, where i = 1,…,N is a country index and j = 1,…,T is a time index) captures the share of the non-active age population, which is economically dependent. It is the size of the young (aged 0–14) and the old (aged 65 and more) population divided by the working age population (aged 15–64). Therefore, \( {dep}_{i,j}=\left({n}_{i,j}^{y oung}+{n}_{i,j}^{old}\right) \) / \( {n}_{i,j}^{working\ age} \). Another variable of interest is the youth dependency ratio, denoted as \( {ydep}_{i,j}={n}_{i,j}^{young}/{n}_{i,j}^{working\ age} \) . It covers the size of the young population (aged 0–14) divided by the working age population (aged 15–64). The third demographic variable is the old-age dependency ratio, \( { old dep}_{i,j}={n}_{i,j}^{old}/{n}_{i,j}^{working\ age} \). It shows the ratio of elderly people to the working age population.

As mentioned in the introduction, the developed world is currently experiencing a shift in the age composition of the population. These demographic changes have already begun in some countries (e.g. Japan). In the analysed period, the average ratio of people aged 65 and more in the society rose from 10% to 16.8% in the sample. Forecasts predict that in the future this share will grow further, reaching as much as 27% in the year 2050. It means that in 2050 every fourth person in the analysed countries will be aged 65 or over.

There is some heterogeneity in the sample. The youngest populations are observed in non-European countries: Mexico and Chile. Interestingly, in those countries the observed inflation rates were among the highest in the analysed period. Another group of countries comprises Korea and Japan. In 1971 Korea was the youngest population in the sample; the ratio of elderly people in the society was only 3%. However, in this country demographic change is occurring very rapidly. In 2015 the analysed ratio in Korea was 13.1%. The predicted value for the year 2050 is 37.4%. This means that Korea’s population ageing is occurring at the fastest pace in the analysed countries. In Japan, population ageing will increase its pace in the near future. In 2050 Japan will be the oldest country in the sample. Besides Japan, the countries with the highest forecasted ratios of elderly people are the European Union members (Spain, Portugal, Italy and Greece).

Looking at the development of the old-age dependency ratio over the analysed period, one can notice that it has been growing steady in most countries in the sample. An interesting outlook is given by the forecasts for the analysed countries (Fig. 1). The forecasted old-age dependency ratios show that not only is the population getting older, but this process will be even stronger in the future. Elderly people will constitute an important and large part of the societies, not only in Japan and Korea, but also in EU economies.

Fig. 1
figure 1

Old-age dependency ratio in selected OECD economies, 1971–2050. Source: OECD database

Full size image

At the same time, we are also experiencing a declining youth dependency ratio, which illustrates the proportion of children in the population (Fig. 2). In the analysed time period, its mean value in the countries in the sample dropped from 45.5% to 25.6%. According to forecasts, it should stabilise at 20–25% by 2050. However, the discrepancy in the sample will shrink. In 1971 the highest youth dependency ratio (97.6%) was in Mexico, while the smallest (29.9%) was observed in Hungary. In 2015 the highest value was only 42.2% and was observed again in Mexico. The lowest youth dependency ratio (19%) was noted in Korea.

Fig. 2
figure 2

Youth dependency ratio in selected OECD economies, 1971–2050. Source: OECD database

Full size image

These developments coexist with another economic trend, which has been recently observed in several ageing countries, namely historically low inflation (Fig. 3). Since 1971 the average inflation rate in the sample dropped from 7.13% to 0.41%. In recent years, inflation rates in some of the analysed countries were even negative. Although for most of the analysed period there is a visible heterogeneity between countries in the sample, in recent years inflation rates have moderated and decreased in all countries. Following Gajewski (2015), the sample has been truncated from above at an inflation rate of 25% in order to exclude periods of sharp macroeconomic instability. Leaving those variables in place could create serious bias in estimation results.

Fig. 3
figure 3

Inflation rates in selected OECD economies, 1971–2014. Source: OECD database

Full size image

Descriptive statistics for the variables used in the model are presented in Table 1.

Table 1 Descriptive statistics for the model variables
Full size table

Empirical Analysis, Results and Conclusions

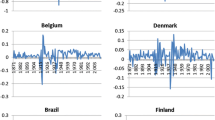
We begin with a simple graphical comparison of two variables – inflation and dependency ratio. A first look at the data (Fig. 4) reveals that there may be some relationship between inflation and demography. In the long-term they seem to correlate. Although only selected economies are presented in Fig. 4, a similar pattern is visible in almost all economies in the sample. However, in the 2010s, one can observe a visible divergence between these variables.

Fig. 4
figure 4

Inflation rate (lhs, %) and dependency ratio (rhs, %) in selected economies. Source: OECD database

Full size image

It has to be noted that inflation may be driven by some common factors across countries, other than demography. Before the late 1980s, inflation was strongly driven by such factors as oil price shocks. Moreover, the dependency ratio was more or less similar across countries. Therefore, this relationship will be checked in the next section.

The general empirical model is given by Eq. (1). It is based on regressing inflation on demographic variables as well as other control variables. In this way, this approach differs from the previous research. There are different non-ageing-related drivers of inflation that we control for.

$$ {\mathit{\inf}}_{i,j}={\alpha}_0+{\alpha}_1\bullet {dep}_{i,j}+{\alpha}_2\bullet {tot}_{i,j}+{\alpha}_3\bullet {m}_{i,j}+{\alpha}_4\bullet {ggdp}_{i,j}+{\alpha}_5\bullet {budbal}_{i,j}+{\varepsilon}_{i,j} $$
(1)

The main variable in the model is the yearly inflation rate, obtained from the OECD database. As low-frequency inflation dynamics are analysed, yearly data are sufficient. The inflation rate is denoted as infi, j, where i = 1,…,N is a country index and j = 1,…,T is a time index. The depi, j variable denotes the dependency ratio (the ratio of non-active age, ie. 0–14 and 65 and more to those of active age, i.e. 15–64 in a population).

To better capture the relations between inflation and demography, control variables are added. The choice of control variables is based mainly on Yoon et al. (2014), who analysed how different demographic variables (such as population growth, shares of specific age groups or life expectancy) influence macroeconomic variables – economic growth, inflation, savings and investment, and fiscal balance. Among the control variables, there are:

tot i,  j :

denotes the yearly change in the terms of trade index (data are taken from the OECD database)

ggdp i,  j :

denotes the annual growth rate of real GDP (Source: OECD database)

m i,  j :

denotes the base money growth rate (Source: IFS)

budbal i,  j :

denotes the annual change of general government deficit (Source: OECD database)

In order to check whether the impact of different dependent age groups on inflation is different, variable depi, j is divided into two categories: youth dependency ratio (ydepi, j) and old-age dependency ratio (olddepi, j). Therefore, Eq. (2) looks as follows:

$$ {\mathit{\inf}}_{i,j}={\alpha}_0+{\alpha}_1\cdot {ydep}_{i,j}+{\alpha}_2\cdot {olddep}_{i,j}+{\alpha}_3\cdot {tot}_{i,j}+{\alpha}_4\cdot {m}_{i,j}+{\alpha}_5\cdot {ggdp}_{i,j}+{\alpha}_6\cdot {budbal}_{i,j}+{\varepsilon}_{i,j} $$
(2)

Before running the regressions, a test to check whether the panel data is stationary was applied. For this type of panel data most suitable is the Im–Pesaran–Shin unit root test, the results of which are presented in Table 2. The results reveal that, besides olddepi, j, all the panel variables are stationary at level. For the variable olddepi, j, we apply a moving average smoother with uniform weights. As a result, a new variable, smmai, j, is created. Testing for stationarity allowing for a constant plus a time trend confirms that the variables are stationary at level.

Table 2 Panel unit root test results (at level)
Full size table

The results of estimations are presented in Table 3. The regression equation parameters are initially estimated using OLS (1). In the first form of the model, with dependency ratio as the only demographic variable, a positive impact on inflation has been observed. The relationship between inflation and demography cannot therefore be rejected. To further check this hypothesis, we perform the regression equation using fixed effects (FE; 2) and random effects (RE; 3). A modified Wald statistics for groupwise heteroscedasticity in the residuals and the Woolridge test for serial correlation show that both problems exist in the panel and should be controlled for (Table 4). As the FE estimator may be inefficient in this panel, we apply a GLS model (4), which analyses panel-data linear models by using feasible generalised least squares. This allows us to estimate in the presence of AR(1) autocorrelation within panels as well as cross-sectional correlation and heteroskedasticity across panels. In this specification, there is indeed a positive relationship between inflation and dependency ratio. The coefficient of variable depi, j is positive (0.089) and significant at the 1% level. These results show the relationship between the overall dependency ratio and inflation. It confirms the results of Yoon et al. (2014) that dependents are inflationary.

Table 3 Estimation results
Full size table
Table 4 Tests for groupwise heteroskedasticity and serial correlation
Full size table

After examining the relationship between the dependency ratio and the inflation rate, the next step is to divide the dependency ratio into its components (youth dependency and old-age dependency ratio) in order to check whether the impact of elderly dependents on inflation differs from the impact of young dependents.

Indeed, different results have been obtained. In each specification the negative and significant effect of increasing old-age dependency ratio on inflation has been confirmed. An increase of the old-age dependency ratio of one percentage point translates into a 0.39 to 0.19 decline in the average inflation rate. This confirms the hypothesis that ageing is deflationary. What is more, this issue gains importance given the current demographic trends and the projected increase in the proportion of elderly people (for the detailed projections see European Commission 2015). Moreover, regardless of the specification, a significant and positive effect of the youth dependency ratio on inflation has been observed. The results are robust to different time periods, control variables and estimation techniques.

To assess the stability of the effect of old-age dependency ratio on inflation with respect to time, we also computed the parameter estimates over a 10-year rolling window (Fig. 5). For most of the analysed period, a small but negative impact of old-age dependency ratio on inflation was confirmed.

Fig. 5
figure 5

Parameter by the variable olddepi, j, 10-year rolling window

Full size image

In order to check the robustness of the results, additional tests were performed. Among them we checked how the analysed parameters varied when different country samples were chosen. Therefore, we divided the sample within the panel into four quartile groups, based on the old-age dependency ratio in 2015. Table 5 presents the results of the estimations made for d = 0, i.e. countries where in 2015 the old-age dependency ratio was the highest.

Table 5 Estimation results for d = 0
Full size table

In this specific sample, the coefficient of the variable depi, j is now negative in all specifications. In model (4), which is most suited for this panel, it is also significant at the 0.01 level. The change of this effect from positive to negative may stem from the fact that in this sample the old-age dependency ratio is relatively high and the youth dependency ratio is relatively small. The group of dependents constitutes mostly elderly people. Splitting the variable depi, j into two seems to confirm this observation, especially in model (8), where the negative impact of old-age dependency ratio on inflation is significant at the 0.01 level. In addition, results for the group of countries with the lowest old-age dependency ratio in 2015 (d = 3) seem to confirm these results (Table 6). In the first form (specifications 1–4), an increase in the number of dependents seems to be inflationary again. However, these are the countries with low olddepi, j and relatively high ydepi, j. Regardless of the specification, the deflationary impact of elderly dependents appears to be confirmed.

Table 6 Estimation results for d = 3
Full size table

The results of this empirical analysis add to the ongoing discussion on the relationship between demography and inflation rate. They suggest that demographic changes may have a deflationary impact in the future, particularly in those economies, where significant population ageing is currently experienced or expected. Similar to Gajewski (2015), we show that there is indeed a relationship between demography and inflation – while old-age dependents are deflationary, young dependents seem to be rather inflationary. What differs from the aforementioned approach are the non-ageing drivers of inflation we control for. The overall impact of dependents on inflation appears to be different for particular age groups.

There are still many research gaps in this field and there is no theoretical nor empirical consensus of the influence of population ageing on demography. If the results presented above are given further empirical support, it would be interesting to test them in more detail, especially using more demographic variables. It is also important to analyse the impact of demographic variables on areas other than inflation rate. Another problem that has not been sufficiently addressed is the impact of ageing on the conduct of monetary policy, as demography as a driver of inflation may be relevant to monetary policymakers in the near future. The macroeconomic policy framework may therefore need to be revisited in the future. Demographic changes are one of the most important long-term challenges for the economy, but they can be relatively well predicted. Thus, the demographic impact of inflation may be taken into account in future monetary policy decisions.