Does economic complexity increase energy intensity?

Abstract

Today, many countries in the world pay special attention to energy efficiency to improve environmental quality and reduce the waste of energy resources. For this purpose, this research has investigated the economic complexity of energy intensity (EI) from 1995 to 2019 using club convergence and panel quantile regression (PQR) models. The club convergence results showed that out of 62 countries, 42 converged in energy intensity during the period. Then, using the PQR model, the determining factors of EI for these 42 countries were evaluated: economic complexity, urbanization, trade openness, industrial production, foreign direct investment, oil price, and economic growth. The result of the PQR model confirmed that economic complexity has an inverted U-shaped relationship with EI. Urbanization and foreign direct investment have a positive and increasing effect on EI. In addition, trade openness positively affects EI, mainly in the 10th and 25th quantiles. On the other hand, economic growth has a decreasing effect on EI. Moreover, industrialization and oil prices can reduce EI, particularly in the 90th quantile. Given the inverted U-shaped effect of the energy complexity on energy intensity, where the lower and higher quantiles are negative, it is advised that policymakers ought to promote the leap from lower levels of economic complexity to higher levels by reducing intermediate levels as much as possible. Policymakers should also be conscious that promoting the diffusion of economic complexity also mitigates noxious gas emissions.

Introduction

Climate change is associated with long-term shifts in weather patterns and temperatures. Despite these variations that may be natural, human activities have been identified as the significant drivers of climate change, mainly because of fossil fuels burning, which yield heat-trapping gases (Adedoyin et al., 2022). Due to the demographic and economic transitions, the pollution mix has switched from greenhouse gas emissions to solid waste and effluents, concluding that the total waste is still high and pollution per capita has not decreased (Sinha et al., 2020). In this regard, environmental degradation, pollution, and loss of biodiversity are discussed as the major improper outcomes of the world’s economic growth (Mealy & Teytelboym, 2020). The International Energy Agency (World Energy Outlook, 2018) reported that economic growth–related efforts and energy intensity concerning carbon-based fuel portfolios have contributed to intensifying climate change in developing and developed countries. On the other hand, due to technological advancements, enforcement of environmental terms and regulations, and environmental sustainability, the level of environmental pollution against economic output has declined in developed countries (Shahzad, 2020).

It is also pointed out that energy consumption structure affects economic growth and is a major cause of environmental degradation (e.g., Mealy & Teytelboym, 2020; and Hanif et al., 2019). Notably, the role of developed energy technologies and innovation in resource diversity, affordable energies, and climate change (Weiss et al., 2021) has strengthened in recent years. This process decreases fossil fuel usage and changes the structure of energy consumption and energy intensity (Wu et al., 2021) and portfolio decisions of primary energy sources (Shirazi & Fuinhas, 2023) throughout the energy systems, which lowers environmental degradation. Energy intensity is mentioned as a proxy to measure energy efficiency and is characterized by various determinants based on the structural features of each economy (e.g., Filipović et al., 2015; and Gonzales et al., 2013). The concept of energy intensity, defined as the ratio of energy consumption to economic output (Guo et al., 2020), covers a range of aspects regarding energy security, energy conservation, and production costs (Ang, 2006), which reflects the energy efficiency level of the energy system. Hence, this research strictly aims to assess the impact of the synergies of technology innovation, structural changes, diversity, and knowledge on energy intensity, which helps countries to adopt comprehensive dynamic energy policies, develop their energy systems, and, therefore, facilitate sustainable economic development.

Earlier articles have not yet explicitly studied all determinants of energy intensity, especially in the context of innovation and structural changes within the energy systems. That is to say, urbanization, economic growth, industrial structure, foreign direct investment, and technological progress are almost investigated throughout the previous related literature to explore the determinants of energy intensity. Notably, economic growth (e.g., Levinson, 2021; Fang et al., 2021; and Antonietti & Fontini, 2019), oil prices, industry value added, urbanization, and the net inflow of foreign direct investment (Antonietti & Fontini, 2019), as well as trade openness and technological advances (e.g., Adom, 2015a; Adom & Kwakwa, 2014; Zheng et al., 2011; and Cole, 2006), have been studied as factors affecting energy intensity. Furthermore, by increasing the suggested determinants, energy intensity’s scale, composition, and technique effects require investigation through knowledge-based and innovation activities (Adedoyin et al., 2022).

However, to lower energy trilemma concerns, the global economy needs to focus on internationally determined contributions to form an image of dynamic behavioral characteristics of the structure of energy consumption and energy intensity (Shirazi, 2022). Specifically, the structural development policies, e.g., technological improvements and environmental sustainability (e.g., Shahzad, 2020; and Golpîra et al., 2018), relative to energy intensity and energy transition, are committed by the economies to reduce emissions (Shahzad et al., 2021). Accordingly, it is no doubt necessary for governments to devise their energy policies to decrease energy intensity and, therefore, increase energy efficiency, primarily through economic complexity as it relates to the medium- and high-tech economies, which researchers do not explicitly focus on as one of the determinants of energy intensity. Specifically, and based on Hidalgo and Hausmann (2009), economic complexity is defined as the combination of knowledge, innovation, productive structure, structural changes, diversity, and capabilities of the economic system that shapes the patterns of the sector and source-based energy consumption of the economies. Laverde-Rojas et al. (2021) mention economic complexity as the quality of the gross domestic product (GDP). Also, economic complexity in the energy system is explained through the theoretical connectedness channel between energy consumption and economic growth, where productivity plays an intermediate role regarding the innovation process and technological improvements (Alvarez et al., 2017).

Nevertheless, to focus on how economic complexity influences energy intensity, it is suggested that economic complexity is affected by an inverted U-shaped pattern due to the scale, composition, and technique effects. Scholars have markedly underscored that economic growth requires much input; hence, more energy sources are applied in the production process. Especially in the first phase and due to the inefficient industrialization process, energy intensity is expected to rise in response to the increase in economic complexity. In this stage, more energy resources are used by underdeveloped and developing technologies, while their environmental consequences are neglected, which leads to scale effects and large energy intensity (Zafar et al., 2019). However, as economic growth increases, the structure of the economies tends to change, called composition effects. Higher knowledge and greater technological and economic progress in this phase lead to cleaner activities and less energy intensity (Dinda, 2004). At high levels of income, underdeveloped and developing technologies are replaced with developed technologies, called technique effects. The technique effects lead to greater productivity, energy efficiency, and energy savings (Bano et al., 2018); hence, lower energy intensity occurs in this stage.

Consequently, the major contribution of this research is to explicitly focus on the impact of economic complexity on low, median, and high quantiles of energy intensity. In detail, this article studies the potential existence of an inverted U-shaped pattern through the relationship between energy intensity and economic complexity via the panel quantile regression from 1995 to 2019. The importance of this novelty is to shed light on the heterogeneous effect of economic complexity on energy efficiency: a small number of works implicitly suggest a positive relationship between energy intensity and economic complexity (e.g., Shahzad et al., 2021; Sarkodie & Strezov, 2018), and of course, the opposite around is found by the other related works (e.g., Fang et al., 2021; and Antonietti & Fontini, 2019).

Also, urbanization, trade openness, industry value added, gross domestic product per capita, net inflow of foreign direct investment, and oil price are other energy intensity determinants considered in this paper. Specifically, it is suggested that energy intensity decreases in response to the rise of GDP per capita (e.g., Levinson, 2021; Fang et al., 2021; and Antonietti & Fontini, 2019). Particularly, economies with higher technological and economic progress face greater energy efficiency. Therefore, lower energy intensity occurs (Antonietti & Fontini, 2019). It is also expected that energy prices negatively affect energy demand and hence, lower energy intensity (Fang et al., 2021). Also, the lower opportunity costs of used oil are why energy intensity shows decreasing changes in reaction to oil price changes.

Moreover, the energy intensity of a country decreases as urbanization increases since greater population density causes higher levels of energy efficiency (Antonietti & Fontini, 2019). Furthermore, the energy efficiency of a country develops when the motivations are increased for the country’s capital inflow. As a result of trade openness, a country’s domestic industries are motivated to participate in the formed competition through technological progress, innovations, and foreign direct investment that leads to energy intensity declines (Adom, 2015b).¹

This paper makes four major steps to follow the aim of our research. First, the nonlinear time-varying factor convergence club model, proposed by Phillips and Sul (2007, 2009), is used to study the convergence between countries. In the second step, after checking the abnormal distribution of the data, we assess the cross-sectional dependence between countries (Belsley et al., 2005). Then, a long-run relationship between energy intensity and the explanatory variables should be satisfied to avoid spurious regression (e.g., Antonietti & Fontini, 2019; Wang et al., 2018; and Al-Mulali & Ozturk, 2016). Finally, the panel quantile regression (e.g., Koenker & Xiao, 2002; and Koenker & Bassett, 1978) is applied to analyze how the explanatory variables affect the energy intensity’s low, median, and high quantiles (e.g., Sevillano & Jareno, 2018; and Jareno et al., 2016).

The remainder of this paper is organized as follows. The literature review is presented in the “Literature review” section. The “Data and method” section provides data and methods. The “Empirical results” section presents the results, while the “Discussion and policy implications” section discusses them and assesses the policy implications. Finally, the conclusions are covered in the “Conclusions” section.

Literature review

The literature does not explore the relationship between energy intensity and economic complexity. A gap in the literature regarding this topic needs to be filled and investigated. Most studies that approach economic complexity are focused on issues related to environmental degradation, ecological footprint, global warming, and energy consumption (e.g., fossil and renewable), leaving aside issues related to energy intensity, as shown in Fig. 1 below that indicates a wordnet of publications related to economic complexity through bibliometric mapping with data from Scopus and Google Scholar.

Fig. 1

Wordnet of publications related to economic complexity. The authors created this bibliometric map using VOSviewer software

This bibliometric mapping was realized through VOSviewer software 1.16.18. In addition, some authors, such as Eck and Waltman (2010) and Koengkan and Fuinhas (2022a, b), used this software to realize bibliometric mapping. From the analysis, one can conclude that (i) ten studies have approached the relationship between economic complexity and energy consumption/energy use/energy utilization, (ii) six studies have approached the relationship between economic complexity and environmental degradation/environmental quality, (iii) four studies have approached the relationship between economic complexity and renewable energy/alternative energy, (iv) three studies have approached the relationship between economic complexity and CO₂ emissions, (v) two studies have approached the relationship between economic complexity and fossil fuels, (vi) one study has approached the relationship between economic complexity and global warming, (vii) one study has approached the relationship between economic complexity and Kuznets curve, and (viii) one study has approached the relationship between economic complexity and energy.

This bibliometric analysis did not identify any literature on economic complexity and energy intensity. For this reason, this empirical research has chosen to use similar studies, i.e., investigations that have approached the relationship between economic complexity and energy consumption (e.g., Can et al., 2022; Can & Ahmed, 2022; Shahzad et al., 2021; Liu et al., 2021; Rafique et al., 2021; Azizi, 2020; Fang et al., 2021; Can et al., 2021; Neagu & Teodoru, 2019; and Bond, 2015). For example, Can et al. (2022) studied the relationship between economic complexity and total energy consumption in 21 developed and 44 developing countries for the period between 1971 and 2014. Indeed, these authors used as method the Durbin-H panel cointegration technique. The empirical results indicated that economic complexity increases energy consumption in developing countries while it decreases energy consumption in developed countries.

Can and Ahmed (2022) explored the effect of economic complexity on the consumption of non-renewable and renewable energy sources for a group of 14 European Union countries in the period between 1990 to 2014. The authors used the stochastic impacts by regression on population, affluence, and technology (STIRPAT) framework to conduct their investigation. Their empirical results indicated that economic complexity increases renewable energy and decreases non-renewable energy use.

Shahzad et al. (2021) investigated the relationship between economic complexity, consumption of fossil fuels, and ecological footprint in the USA. The authors used quantile autoregressive distributed lag (QARDL) and quantile Granger causality tests for the period between 1965Q1 to 2017Q4. The empirical results indicated that economic complexity and fossil fuel energy consumption significantly enhance the ecological footprint in the USA. Furthermore, the quantile causality empirics suggested causal relationships between economic complexity and energy consumption with the ecological footprint. Liu et al. (2021) studied the correlation between energy consumption (e.g., renewable and fossil fuels energy sources) and economic complexity. This investigation used the Lancang-Mekong Cooperation countries between 1990 to 2017. The authors used a panel vector autoregression (PVAR). Their analysis’s empirical result shows a unidirectional relationship between energy consumption and the economic complexity index. Furthermore, they verified that renewable energy usage is a possible alternative to traditional energy and can increase economic complexity.

Rafique et al. (2021) examined the heterogeneous impacts of economic complexity on renewable energy demand within a panel of G7 countries (e.g., Canada, France, Germany, Italy, Japan, the UK, and the USA) and E7 countries (e.g., China, India, Brazil, Turkey, Russia, Mexico, and Indonesia). The authors used the feasible generalized least squares (FGLS), system Gaussian mixture model (GMM), fully modified ordinary least squares (FMOLS), and dynamic ordinary least squares (DOLS). The results indicated that economic complexity affects renewable energy demand from G7 and E7 countries. Therefore, economic complexity is a policy factor for overall energy transformation and greener energy demand. Moreover, the authors recommend that complexity and structural change policies be observed for cleaner and greener growth and overall greener energy promotion. Azizi (2020) used a smooth transition regression model to identify the effect of economic complexity on energy consumption in Iran from 1971 to 2013. The model estimation results confirm a nonlinear relationship between per capita income, real energy price index, and the economy’s complexity with per capita energy consumption. Also, economic complexity leads to a two-regime structure with a threshold of − 1.15. So in the first regime, which is related to the low levels of economic complexity, the effect of this variable on energy consumption was positive, which could be due to the rebound effects of technology on energy consumption. However, in the second regime, which is related to higher levels of complexity, the relationship was negative. Therefore, improving the complexity level in the second regime can help save energy. On the other hand, the elasticity of income and price in both regimes was less than one. As the complexity passes the threshold, the elasticity increases concerning price, which indicates that with the increase of technology and knowledge of the country, the power of consumers’ reaction to the price changes will increase.

Fang et al. (2021) explored the role of economic complexity on energy demand using a panel dataset of 25 of the Organization for Economic Co-operation and Development (OECD) countries from 1978 to 2016. Moreover, the results from using the augmented mean group (AMG) estimations illustrate that real per capita income level positively affects energy demand while real energy price and economic complexity negatively influence it. The authors suggested that increasing technological innovation (i.e., higher economic complexity) will reduce energy demand. Reducing massive energy usage may benefit the natural environment’s health in the OECD countries.

Can et al. (2021) investigate the composition impact of the trade by using export product diversification, extensive margin, and intensive margin on energy use and environment in ten newly industrialized countries (NICs) from 1970 to 2014. The authors used the STIRPAT framework to conduct their empirical investigation. The empirical results showed that the composition of export products, income, urbanization, and economic complexity promotes energy use and CO₂ emissions.

Neagu and Teodoru (2019) examined the long-term relationship between economic complexity, energy consumption structure, and greenhouse gas emission within a panel of European Union countries and two subpanels: (i) European economies with higher economic complexity and (ii) European economies with a lower level of economic complexity. The authors used the FMOLS and DOLS. The empirical findings indicate a long-term equilibrium relationship between economic complexity, energy consumption structure, and greenhouse gas emission within all three panels. Moreover, economic complexity and energy consumption structure statistically impact greenhouse gas emissions within all panels. Still, the influence is bigger within the subpanel of countries with lower economic complexity, suggesting a higher risk of pollution as the economic complexity grows and the energy balance inclines in favor of non-renewable energy consumption. Finally, Bond (2015) investigated the effect of economic complexity on energy consumption in a panel of 40 countries between 1995 and 2011. The author identified the existence of the positive impact of economic complexity on the consumption of energy.

In this section, we realize a brief literature review indicating the main authors that studied economic complexity’s effect on energy consumption. However, this literature review identified the existence of different conclusions by using different methodologies, variables, periods, and countries or regions, leading to a non-consensus about the impact of economic complexity on energy consumption. Indeed, due to this, it is essential the realization of more studies on this topic.

Moreover, in this literature review, we found some gaps which need to be filled. The first and the most significant is the absence of studies investigating the impact of economic complexity on energy intensity. All reviewed studies solely explored this impact on energy consumption, as shown in Fig. 1 above. This scenario shows that the relationship between energy intensity and economic complexity is unexplored and calls for further investigation. Another gap found is the non-use of club convergence and panel quantile models together, which will bring some advantages to the study of this topic. Most studies that investigated the impact of economic complexity on energy consumption used the quantile model regression and ordinary least squares or method of moments (see Fig. 2 below).

Fig. 2

Wordnet of publications related to economic complexity. The authors created this bibliometric map using VOSviewer software

In the next section, we will present/explain the data and method used in this article.

Data and method

In this section, we exposed the data used and the methodology followed in this research. The first subsection, “Data,” contains the database/variables, and the second subsection, “Method approach,” includes the research method.

Data

This study explores the determinants of (i) energy intensity, e.g., economic complexity (Adedoyin et al., 2022); (ii) GDP per capita (e.g., Levinson, 2021; Fang et al., 2021; and Antonietti & Fontini, 2019); (iii) oil prices; (iv) industry value added (Antonietti & Fontini, 2019); (v) urbanization; and (vi) the net inflow of foreign direct investment (Antonietti & Fontini, 2019), as well as (vii) trade openness (e.g., Adom, 2015a; Adom & Kwakwa, 2014; Zheng et al., 2011; and Cole, 2006), that may lead to fewer economic costs of transforming energy sources into production, and therefore, sustainable economic development can be accelerated (Adom & Amuakwa-Mensah, 2016). The period in this study is from 1995 to 2019. The reason for using this period is the availability of data in this period. The variables used in this research are listed below:

• Energy intensity (EI).

• Economic complexity index (ECI).

• Urbanization (URB).

• Trade openness (TO).

• Industry value added (% GDP) (IND).

• Gross domestic product per capita (GDP) based on constant 2010$ (USD).

• Foreign direct investment, net inflow (% GDP) (FDI).

• Oil price constant 2010$ (OILP).

This section defines the variables and databases (see Table 1 below), and more about statistic specifications is provided in the experimental results. In addition, the entire countries list is available in the Appendix. Because first, using the club convergence among 62 countries, convergent countries are selected in energy intensity, and then we continue to analyze those countries using quantile panel regression.

Table 1 Variable acronyms, definitions, and sources

Method approach

In this study, two methods have been used. The first subsection, “Club convergence,” includes the club convergence method, and the second subsection, “Panel quantile regression (PQR),” indicates the panel quantile regression. Indeed, in order to identify the possible effect of economic complexity on energy intensity, the subsequent methodology framework will be followed (see Fig. 3 below).

Fig. 3

Methodology framework. The authors created this figure

Club convergence

The Phillips and Sul (2007, 2009) convergence test is based on a time-varying nonlinear factor model that examines the convergence between countries/regions using stationary or non-stationary data. The relative advantage of this method is that it does not rely on any assumptions about the fix of variables, such as random convergence tests (e.g., Apergis et al., 2012; and Payne & Apergis, 2020). In this model, a common time-varying component is used (see Eq. 1 below):

$${\mathrm{EI}}_{it}={\delta }_{it}{\mu }_{t,}$$

(1)

where EI indicates the energy intensity in country i at time t. ${\mu }_{t}$ is a permanent component, and ${\delta }_{it}$ is an idiosyncratic component and time-varying. The ${\delta }_{it}$ component measures the deviation between EI and the common component ${\mu }_{t}$. Since ${\delta }_{it}$ is not directly estimated from Eq. (1) above due to the over-parameterization, Phillips and Sul (2007, 2009) use the relative transfer parameter, h_it, as follows (see Eq. 2 below):

$${h}_{it}=\frac{{\mathrm{EI}}_{it}}{\frac{1}{N}\sum_{i=1}^{N}{\mathrm{ECI}}_{it}}=\frac{{\delta }_{it}}{\frac{1}{N}\sum_{i=1}^{N}{\delta }_{it}}$$

(2)

${h}_{it}$ considers the relative transition path according to the panel average, where ${\delta }_{it}$ measures the average relative panel. Thus, the transition path for EI in country i is relative to the panel average. When ${\delta }_{it}$ converges to the constant δ, then the relative transition path for country i, ${h}_{it}$ converges to 1 (t → ∞), as follows (see Eq. 3 below):

$${H}_{t}=\frac{1}{N}\sum_{i=1}^{N}{({h}_{it}-1)}^{2}\to 0$$

(3)

Formal econometric tests such as convergence club require the assumption of a semi-parametric form of the time-varying ${\delta }_{it}$ as follows (see Eq. 4 below):

$${\delta }_{it}={\delta }_{i}+\frac{{\sigma }_{i}{\xi }_{it}}{L(t){t}^{\propto }} ,$$

(4)

where ${\delta }_{i}$ is constant; ${\xi }_{it}$~ iid (0,1) is varies in countries i = 1, 2, …, N; ${\sigma }_{i}$ is a specific scale parameter; L(t) is a slowly varying function, and when t → ∞, L(t) is infinitely divergent; ∝ shows convergence speed. Equation 4 above shows that ${\delta }_{it}$ converges to ${\delta }_{i}$ when ∝  ≥ 0. Hence, the null convergence hypothesis is as follows (see Eq. 5 below):

$$\left\{\begin{array}{c}{H}_{0}: {\delta }_{i}=\delta \; and\propto \ge 0\\ { H}_{A}: {\delta }_{i}\ne \delta \; or\propto <0\end{array}\right.$$

(5)

Phillips and Sul (2007, 2009) state that log t regression can be used to test convergence, and the clustering algorithm can be used to identify convergence clubs as follows (see Eq. 6 below):

$$\log\left(\frac{H_1}{H_2}\right)-2\;\log\;L\;\left(t\right)=\widehat a+\widehat b\;\log\;t\;+\;\varepsilon_t$$

(6)

For t = rT, rT + 1, …, T where r > 0 is set in the range (0.2, 0.3). For $\widehat{b}=2a$, the null hypothesis for the one-way test considers $\widehat{b}\ge 0$ versus $\widehat{b}<0$. The t-test statistic follows the standard normal distribution asymptotically and is constructed using a standard error consistent with heteroscedasticity and autocorrelation. Phillips and Sul (2007) call the one-way t-test based on ${t}_{b}$, the “log t-test” in Eq. (6) above.

Phillips and Sul (2007, 2009) club convergence step to identify convergent groups proceeds as follows:

• 1. Arrange the countries in descending order of the value of the last period of the time series

• 2. The next step is to select k to form each club using Eq. 6 (2 < k < N); k is the number of club members. The criterion for choosing the size of the main group ${k}^{*}$ is that ${k}^{*}={\mathrm{argmax}}_{k}\{{t}_{k}\}$ for $\mathrm{min}\left\{{t}_{k}\right\}>-1.65$ for k = 2, 3, …, N.

• 3. Add one country to the core club each time from the remaining countries, recalculate Eq. (6), and test convergence with the log t-test.

• 4. Repeat the above steps for the remaining countries (if any) until other clubs do not converge. Finally, countries whose convergence is not confirmed are considered non-convergent.

Panel quantile regression (PQR)

Quantile regression was introduced by Koenker and Bassett (1978). This model is used when the data distribution is abnormal because the OLS model assumes a normal data distribution at all points and therefore does not provide a reliable estimate. The quantile panel regression provides a reliable model by estimating different quantiles (Koenker, 2004).

Therefore, this study uses the quantile panel regression method to evaluate the effect of economic complexity on energy intensity. The mathematical formula of this model is given in Eq. (7) below.

$$\begin{array}{l}{y}_{i}={x}_{i}{b}_{\theta i}+{\mu }_{\theta i}. \;0<\theta <1\\ {\mathrm{Quant}}_{i\theta }({y}_{i}/{x}_{i})={x}_{i}{\beta }_{\theta },\end{array}$$

(7)

where x and y represent the vector of independent variables and dependent variable, respectively; μ is a random error whose conditional quantile distribution is zero; ${\mathrm{Quant}}_{i\theta }({y}_{i}/{x}_{i})$ is the $\theta \mathrm{th}$ quantile of the explanatory variable; the β_θ estimate shows the quantile regression θth and solves Eq. (8) below:

$$\mathrm{min}\sum \limits_{yi\ge {x}_{i}^{^{\prime}}\beta }\theta |{y}_{t}-{x}_{i}^{^{\prime}}\beta |+\sum_{yi<{x}_{i}^{^{\prime}}\beta }\left(1-\theta \right)|{y}_{t}-{x}_{i}^{^{\prime}}\beta |$$

(8)

As θ is equal to different values, different parameter estimations are obtained. The median regression is a particular case of quantile regression under θ = 0.5 (Xu & Lin, 2018).

According to econometric theories, a logarithmic model of variables has been used to exclude possible heterogeneity phenomena (see Eq. 9 below):

$${\mathrm{LEI}}_{it}=\mathrm{La}+{\beta }_{1}{\mathrm{LECI}}_{it}+{\beta }_{2}{\mathrm{LGDP}}_{it}+{\beta }_{3}{\mathrm{LTO}}_{it}+{\beta }_{4}{\mathrm{LIND}}_{IT}+{\beta }_{5}{\mathrm{LURB}}_{it}+{\beta }_{6}{\mathrm{LFDI}}_{it}+{\beta }_{7}{\mathrm{LOILP}}_{it}+{\delta }_{it.}$$

(9)

where EI represents energy intensity, ECI is the economic complexity index, GDP is gross domestic product per capita (constant = 2010$), TO is trade openness, IND denotes industry value added (% GDP), URB is urbanization, FDI indicates foreign direct investment (net inflow), and OILP is oil price (constant = 2010$).

Given that in this study, we used panel quantile regression to assess the effects of the covariates on energy intensity, Eq. (9) above is converted to the following form:

$$\begin{array}{c}{Q}_{\tau }\left({\mathrm{EI}}_{it}\right)=({\mathrm{La})}_{\tau }+{\beta }_{1\tau }{\mathrm{LECI}}_{i\tau }+{\beta }_{2\tau }{\mathrm{LGDP}}_{i\tau }+{\beta }_{3\tau }{\mathrm{LTO}}_{i\tau }+{\beta }_{4\tau }{\mathrm{LIND}}_{i\tau }+{\beta }_{5}L{\mathrm{URB}}_{it}\\ {\beta }_{6\tau }{\mathrm{LFDI}}_{i\tau }+{\beta }_{7\tau }{\mathrm{LOILP}}_{i\tau }+{\delta }_{i\tau }\end{array}$$

(10)

In this regard, ${Q}_{r}$ means the estimation of the quantile regression $\tau \mathrm{th}$ in the energy intensity (EI) and ${(la)}_{r}$ is the constant component. The coefficients ${\beta }_{1\tau }.{\beta }_{2\tau }.{\beta }_{3\tau }.{\beta }_{4\tau }.{\beta }_{5\tau }.{\beta }_{6\tau }.{\beta }_{7\tau }$ are the quantile regression parameters and show the influencing factors.

Empirical results

This section consists of three sub-sections: the first sub-section, “Club convergence results,” indicates the club convergence results. The second sub-section, “Preliminary tests,” includes preliminary tests, and the third subsection, “Panel quantile results,” shows the quantile panel regression results.

Club convergence results

In this section, we present the convergence model of the convergent countries club. These model groups countries that converge over time. In this study, we used energy intensity to examine club convergence between 62 countries. The results of the club convergence in panel A (see Table 2 below) show that since the T-statistic is ${t}_{\widehat{b}}=-49.2599,$ and it is less than (${t}_{\widehat{b}}<-1.651$), it can be stated that there is no full sample convergence between all countries. However, the lack of overall convergence between all countries does not mean they lack convergence in subgroups. Preliminary results of these subgroups (panel A) show that there are five subgroups, and because their t-statistic is higher than − 1.651, the convergence of all subgroups is confirmed. The club convergence model merges these subgroups in the next step, which is outlined in panel B. The merger results of the subgroups indicate that only clubs 2 + 3 can be merged, and the rest cannot.

Table 2 Results of the energy intensity based on club convergence (62 countries)

In panel C, the results are given after merging the subgroups. The final convergence shows that there are four subgroups. For this purpose, in our research, we used club 1 with 42 countries for analysis. The final club compositions are available in the Appendix.

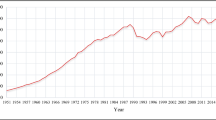
After the club convergence results and selecting club 1, the following is a graph of the energy intensity convergence of these countries during the period (see Fig. 4 below). As can be seen, the energy intensity of these countries converges over time.

Fig. 4

Energy intensity of 42 selected countries. The authors created this figure

Preliminary tests

In this section, after selecting the convergent countries using the club convergence model, the following (see Table 3 below) displays the statistical specifications for the variables. Then, we perform preliminary tests before estimating panel quantile regression (Koengkan & Fuinhas, 2022a). The first important test in this field is the normality test because one of the main assumptions of using panel quantile regression is the abnormal data distribution. Then, multicollinearity tests, cross-sectional dependence, unit root, and cointegration are given, respectively.

Table 3 Descriptive statistics

Table 3 below shows the statistical characteristics of the variables, including the number of observations, mean, standard deviation, minimum, and maximum.

After introducing the statistical specifications of data, we examine its distribution. When data is abnormally distributed, using OLS regression is inefficient because it cannot accurately estimate the data at the beginning, middle, and end points (Koengkan et al., 2022a). For this purpose, quantile panel regression is used (e.g., Koengkan et al., 2022b; and Koenker & Xiao, 2002). This study examines the data for normality using Shapiro–Wilk (Royston, 1992) and Shapiro-France (Royston, 1983) tests. The results of both tests (see Table 4 below) indicate that all variables are significant at a 1% level, which indicates the abnormal distribution of variables. Due to the confirmation of the data abnormality, the quantile panel regression can be used.

Table 4 Normal distribution test

In Table 5 below, we examine the multilinearity of variables and cross-sectional dependencies. This study used the variance inflation factor (VIF) to examine multilinearity (e.g., Kazemzadeh et al., 2022; and Belsley et al., 2005). Given that the VIF values for all variables are less than the standard value of 10 and the average VIF is 1.82, and it is less than the accepted value of 6, it can be said that there is no multilinearity serious problem (Koengkan & Fuinhas, 2022b). The Pesaran CSD test was used to examine the cross-sectional dependence (Pesaran, 2004). The null hypothesis in this test is the absence of cross-sectional dependence. As seen (see Table 5 below), the null hypothesis is rejected for all variables.

Table 5 VIF and CSD test

Since the existence of cross-sectional dependence was confirmed, the panel unit root test (CIPS) by Pesaran (2007) is used (see Table 6 below). Therefore, the null hypothesis in this test is the existence of a unit root. As can be seen, the results of the unit root test (CIPS) show that the EI is stationary at a 5% (with trend) significance level. Furthermore, ECI and FDI are stationary (with and without trend) at a 1% significance level. Therefore, the natural logs of the unit root test show that the variables are stationary (Koengkan et al., 2022c).

Table 6 Panel unit root test (CIPS)

Considering the stationary of all variables in the natural logs, in the following, the existence of a long-term relationship in the variables is investigated using the cointegration test. Westerlund’s (2007) test was used to examine cointegration in this study. The null hypothesis states the absence of cointegration. The results of this test (see Table 7 below) show the rejection of the null hypothesis and the existence of a long-run relationship.

Table 7 Westerlund cointegration tests

Panel quantile results

After conducting preliminary tests, we divided the 42 selected countries into six groups based on the average energy intensity for each country (see Table 8 below). Then, quantiles 10th, 25th, 50th, 75th, and 90th are used to estimate quantile panel regression.

Table 8 Country distribution of energy intensity

Table 9 below shows the results of the panel quantile regression estimations. Furthermore, a fixed-effects panel is also used to evaluate the robustness of the model results. As can be seen, the results of the fixed effects panel show that the LECI, LURB, LIND, and LTO have positive and significant effects on energy intensity. On the other hand, LGDP and LOILP have negative and significant effects on energy intensity. This result confirms the panel quantile regression estimates.

Table 9 Estimation results from panel quantile regression model and panel fixed effects

In this section (see Table 9 above), we evaluate the results of quantile panel regression. As can be seen, economic complexity (LECI) in the quantile 50th has a significant positive effect on energy intensity (LEI), but in the quantiles 10th and 90th, economic complexity reduces energy intensity. According to the quantile coefficients and Fig. 5 below, it is well confirmed that the economic complexity has an inverted-U relationship with energy intensity. Thus, when the LECI level rises, energy intensity increases; after quantile 50th, when the LECI level increases, it gradually reduces the energy intensity rate. Finally, energy intensity decreases in countries with the highest economic complexity levels (above 90th). As can be seen, urbanization (LURB) at all quantile levels has positive and significant effects on energy intensity (LEI). As the coefficients show, this effect is greater at higher quantiles. The results show that increasing urbanization is one of the most important reasons for increasing energy intensity. Furthermore, the results show that trade openness (LTO) in quantiles 10th, 25th, and 90th has increasing positive and significant effects on energy intensity (LEI). Besides, these effects are greater on the energy intensity (LEI) at quantiles 10th and 25th than at other levels.

Fig. 5

Quantile estimates: Shaded areas are 95% confidence bands for the quantile regression estimates. The vertical axis shows the elasticities of the explanatory variables. The red horizontal lines depict the conventional 95% confidence intervals for the OLS coefficients

As seen in Table 9 above, industrialization (LIND) has positive and significant effects on energy intensity (LEI) at all quantiles. Initially, the energy intensity increases from quantiles 10th to 75th with increasing countries’ industrialization levels, and then this effect decreases. It can be said that industrialization has a U-inverse relationship with energy intensity, and in developed industrial countries, energy intensity is less than in other countries. Foreign direct investment (LFDI) has a slight positive and significant effect on energy intensity only in quantiles 75th and 90th. In other quantiles, this effect is not significant. The results show that economic growth (LGDP) in all quantiles except the 50th has significant negative effects on energy intensity (LEI), and these effects are greater at high levels of economic growth. The results show that oil prices (LOILP) in the 25th, 50th, and 90th quantiles significantly negatively affect energy intensity (LEI). These results also confirm that rising oil prices have a greater impact on reducing energy intensity.

Moreover, Fig. 6 below summarizes the effect of independent variables on the dependent ones. This figure was based on results from Table 9 above.

Fig. 6

Summary of the effect of independent variables on the dependent ones. The authors created this figure

Discussion and policy implications

Discussion

Energy intensity varies widely across countries and over time. Countries’ economic structure, access to energy sources, and climate are among the many factors that influence their energy consumption. Thus, to study the determinants of energy intensity, it is crucial to consider a homogeneous group of countries and exclude those with specific idiosyncratic conditions which may contaminate the estimation results. First, we grouped the countries according to their energy intensity using the Phillips and Sul (2007, 2009) club convergence test to achieve this goal. Then, we chose the countries in the first club, which share a decreasing trend in energy intensity, and analyzed the factors that explain its evolution.

Economic complexity indicates a country’s capability to produce diverse goods and services (Hidalgo & Hausmann, 2009). Often, it is seen as a proxy for technological innovation. Thus, complex economies possess environmentally friendly technologies which may decrease energy intensity. However, this improvement in energy efficiency may increase energy services usage (rebound effect) and increase the purchasing power directed to the consumption of other goods and services (Ghosh & Blackhurst, 2014), counteracting the direct effect of better technology on energy intensity. Thus, the impact of economic complexity on energy intensity is, eminently, an empirical matter. However, Table 9 above reveals that the former effect prevails on the lowest and highest quantiles, while the latter dominates on the middle ones. This result is consistent with Azizi (2020), who finds a nonlinear relationship between economic complexity and per capita energy consumption.

Our results reveal that urbanization increases energy intensity. It agrees with prior studies (e.g., Adom & Kwakwa, 2014; Sadorsky, 2013) but contrasts with Antonietti and Fontini (2019), who report that urbanization reduces energy intensity. Furthermore, it is more severely felt in the least energy-efficient countries (highest quantiles).

An increase in the trade may have differing effects on energy intensity, depending on the export structure of each country. Those whose export sector is tilted towards highly polluting and energy-intensive sectors may experience a deterioration of energy efficiency, as trade openness stimulates production in these sectors. In contrast, those that export energy-light products may benefit. Table 9 above also shows that trade openness increases energy intensity, suggesting that these countries export mostly energy-intensive goods. In this study, the former effect prevails, which corroborates the conclusions reached by Zheng et al. (2011), but is at odds with Adom (2015a) and Adom and Kwakwa (2014).

Countries that rely markedly on industrial production to generate income are expected to show a high energy consumption, as this sector considerably depends on this production factor. Our results confirm this conjecture, as do Adom (2015a) and Antonietti and Fontini (2019). The elasticity of energy efficiency to the value-added industry share fluctuates around 0.5 in the lowest quantiles and decreases to 0.19 in the highest one.

Foreign direct investment is often seen as a blessing, as it creates jobs, increases wealth, and promotes technological transfer, leading to higher energy efficiency in the receiving country. However, unfortunately, the foreign investment of rich countries’ firms sometimes aims to escape strict environmental regulations in their home countries and is directed towards highly polluting and energy-intensive sectors (the pollution haven hypothesis). Our results show that the latter hypothesis prevails, and foreign direct investment increases the energy intensity of the recipient countries. This result contrasts with Adom (2015a), Adom and Kwakwa (2014), and Zheng et al. (2011), who report that foreign direct investment enhances energy efficiency.

Oil price increases stimulate the adoption of energy-efficient technologies and energy conservation (Fang et al., 2021). Consequently, countries with higher energy intensity are the most affected by price increases and stand to benefit the most from the technological transition to energy-light processes and energy savings. Thus, the rise in energy prices should positively impact these countries, as our results confirm (see Table 9 above).

Finally, economic growth has a twofold impact on energy intensity. Firstly, wealthy economies have access to advanced energy-efficient technologies, and the share of services in GDP is high. Secondly, as people experience improved material well-being, they begin demanding stricter environmental regulations that promote energy savings and efficiency. Both these channels contribute to the decrease in energy intensity, which finds support in our results, Levinson (2021), Fang et al. (2021), and Antonietti and Fontini (2019).

Policy implications

This study raises several questions that have policy implications. First, reducing energy intensity implies efficiency gains in using energy to produce goods and services. However, policymakers should beware that the rebound effects can hamper improving efficiency. Consequently, other policy measures must be taken to mitigate the undesired effects of efficiency gains on the environment. Second, given the inverted U shape of the energy complexity on energy intensity, where the lower and higher quantiles are negative, it is advised that policymakers ought to promote the leap from lower levels of economic complexity to higher levels by reducing intermediate levels as much as possible. Third, policymakers should be conscious that promoting the diffusion of economic complexity also mitigates noxious gas emissions. Fourth, urbanization increases energy intensity. Thus, policymakers must intervene to reduce transportation congestion and promote less energy-intensive lifestyles. They should also design construction codes that enhance the energy efficiency of buildings. Fifth, foreign direct investment is sometimes used to transfer undesired industries from rich and highly regulated countries to less regulated ones. Given that we have only one Earth, international policymakers must fight these destructive practices and attempt to attract environmentally friendly investments. Sixth, trade openness increases energy intensity, especially in lower quantiles. This result recommends policy measures to reduce energy in the distribution sector. Policymakers should also support energy-light and high-value-added industries to avoid being locked in an export pattern that relies on energy-intensive products. Seventh, the industry is a huge energy consumer. That contributes to increasing the energy intensity, mainly in the higher quantiles. This supports that policymakers should invest in research and development of energy efficiency in industries that are high consumers of energy. They should also subsidize the adoption of energy-efficient technologies. Finally, increases in oil prices stimulate energy efficiency, particularly in the higher quantiles. This finding supports that policymakers can use the price of energy to provoke improvements in energy efficiency.

Conclusions

Understanding the drivers of energy intensity is central to the transition effort to a decarbonized economy. Indeed, energy intensity differs broadly among countries and periods under analysis. Differences can result from several factors, for example, the structure of their economies, the kind of energy used, or even the climate. Economic complexity is significant in how economies can handle energy transition and environmental challenges. Oddly, a link between economic complexity and energy intensity is almost absent in the energy economics literature. Thus, the major contribution of this research is to explicitly focus on the direct impact of the quantiles of economic complexity on energy intensity. Our study also tries to fill another gap found in the literature, the non-use of club convergence and panel quantile models simultaneously. This combination of techniques brings advantages to this topic’s study, namely allowing the selection of more homogenous panels and coping with non-linearities.

Our research focuses on a panel of countries that share convergent features in their energy intensity to reduce the lack of homogeneity. To limit the arbitrariness of the choice of countries, we chose to use the club convergence technique. Since energy intensity is a ratio, its relationship with the explanatory variables is expected to be nonlinear. The panel quantiles technique was used to cope with no linearity of energy intensity. The main factors driving a worldwide panel of energy intensity club convergent of forty-two countries were analyzed from 1995 to 2019, using club convergence tests and panel quantile estimations.

Multiple channels influence energy intensity. Therefore, the energy intensity determinants, economic complexity, urbanization, trade openness, industrial production, foreign direct investment, oil prices, and economic growth were assessed. Panel quantile confirmed that the economic complexity has U-inverse related to the energy intensity. Urbanization and foreign direct investment have a positive and increasing effect on energy intensity. Trade openness positively affects energy intensity, mainly in the 10th and 25th quantiles. On the other hand, economic growth has a decreasing effect on energy intensity. Furthermore, industrialization and oil prices have a noticeable capacity to reduce energy intensity, particularly in the 90th quantile.

Some possible limitations of this study should be stressed. First, the study of the link between economic complexity and energy intensity is in its infancy. It probably requires more time to capture the long-run trends in this link than possible with the short period from 1995 to 2019 we have available. Second, it is far from obvious what econometric techniques should be used and the control variables required to achieve a well-specified model. Third, the annual data frequency is likely too long to catch the dynamics of equilibrium among variables. Finally, we use only proxies of the concrete variables required to assess the relationship between economic complexity and energy intensity.

This research put several questions to the linkage between economic complexity and energy intensity that will require further investigation. For example, the particularities of macroeconomic data operating via means possibly mask divergent behaviors in economic agents. Indeed, means eludes diversity, and improving the analysis with more detail (microeconomic approaches) will allow refined conclusions to use in policymaking. On the other hand, the study process to handle the countries’ heterogeneity given procedures to select more homogeneous countries is necessary to improve the empirical analysis.

The more obvious way to expand this research is to explore other forms of economic complexity and energy intensity to assess the regularity of found results. Another possibility is to look at how countries’ specific characteristics (e.g., climate, demographics) influence the relationship between economic complexity and energy intensity. Finally, this topic must be mixed with pressing problems facing humanity, such as economic development, energy transition, global warming, and population growth.

Appendix

Countries list: Algeria, Argentina, Australia, Austria, Azerbaijan, Bangladesh, Belarus, Belgium, Brazil, Bulgaria, Chile, China, Colombia, Cyprus, Czech Republic, Denmark, Ecuador, Egypt, Finland, France, Germany, Greece, Hungary, India, Indonesia, Iran, Ireland, Italy, Japan, Kazakhstan, Luxembourg, Malaysia, Mexico, Morocco, New Zealand, Norway, Oman, Pakistan, Peru, Poland, Portugal, Romania, Russian Federation, Saudi Arabia, Singapore, Slovakia, South Africa, South Korea, Spain, Sri Lanka, Sweden, Switzerland, Thailand, the Netherlands, the Philippines, the UK, the USA, Turkey, Turkmenistan, Ukraine, Uzbekistan, and Vietnam.

Table 10

Table 10 Final club classifications