Introduction

Energy efficiency, sustainability, and decarbonizing are nowadays common terms regarding the industrial field. There is much literature regarding the consumption of energy worldwide (Berg, 2015). In particular, ceramic industry has been extensively studied as a general subject from an energy perspective. Agrafiotis and Tsoutsos (2001) analyzed all the energy-saving technologies developed during the two last decades of the past century. However, most of the literature is focused on the tile field rather than sanitary-ware manufacturing. The approach of CO2 reduction has been considered by some authors (Ros-Dosdá et al., 2018), who analyzed the tiles industry to meet the European targets regarding decarbonizing. Ciacco et al. (2017) analyzed the energy consumption for the Brazilian tile manufacturing industry.

Research covers different aspects of efficiency and sustainability. In Mezquita et al. (2017), differences of consumptions for both water and energy within the tile manufacturing during slip preparation through selected raw materials were analyzed. Another example dealing with raw materials is that of Wang (2018), where the savings from using wollastonite as a base material were analyzed.

In the pursuit of efficiency and cleanness, sometimes, they may appear restrictions to carry out the possible improvements as studied in da Silva et al. (2017), which considers the efficiency problem for the red ceramic industry. Different factors that restrict the implementation of green technologies have been analyzed. Saving energy measures for the tile industry may be useful for other ceramic sectors. However, they do cover the scope of the sanitary-ware manufacturing. In this regard, this research aims to fulfill this sector by analyzing the specific processes and their variability through the operation cycles.

Sanitary-ware industrial sector is particularly interesting from the thermal point of view. The great thermal power required to manufacture sanitary-ware articles is required in different sub-processes of the factory at different thermal levels. As a matter of fact, the temperature and amount of residual heat from firing is highly suited to supply other heating processes as drying or heating. The recovery of heat waste from firing process is in line with Urbaniec et al. (2016), wherein the waste from one system was used as the resource for another.

The way to apply thermal engineering to save up to one third of the energy can be demonstrated. As suggested in Rehfeldt et al. (2018), thermal requirements are demanded at different levels within the EU region. In 2012, 1035 TWh were demanded over 500 °C, 706 TWh in the range of 100–500 °C, and 228 TWh below 100 °C. From an energy point of view, there has been much research regarding heat recovery but not specifically for the sanitary-ware industry. In Karellas et al. (2018), the potential of waste heat recovery in the EU ETS glass industry according the latest BAT for the ceramic industry is explored.

In this regard, this research furthers the mapping of energy saving provided by Cuviella-Suárez et al. (2018) utilizing it to calculate the actual savings and has contributed to extend the work done there by applying the management tool directly to the modeled factories and quantifying their savings of NG. Delpech et al. (2017) described the general ceramic process and the potential heat recovery from kiln exhausting applicable to the sector. Nevertheless, the procedure is not described but evaluated as a potential ratio which is extended to other fields such as steel or concrete manufacturing. In Jouhara et al. (2018), the state-of-the-art heat recovery potential and its applications in different industrial sectors by different applicable technologies were analyzed. In particular, for the tile industry, Mezquita et al. (2014) found that the residual heat from high temperatures is thermally suitable for direct recovery through thermal processes, such as drying or heating.

Through the different innovative techniques to recover waste heat, some are aiming the ceramic field such as Delpech et al. (2018), where a set of radiative pipes recover thermal energy from cooling air in a kiln for firing tiles, or Delpech et al. (2019) who proposed the recovery through radiative ceiling to heat air for drying process. Also, aiming tile manufacturing, Egilegor et al. (2020) discussed the use of heat pipe heat exchangers. Some research has been devoted to set a procedure of heat recovery such as that of Woolley et al. (2018), stating a guide with four steps to assess the potential of heat recovery.

Modeling has been the technique selected to calculate the variables of this study. It has been carried out for both continuous and shuttle kilns in order to assess the variability of the waste heat available through the duty cycles. In this line of research, there are similar articles. Milani et al. (2017) and Nicolau and Dadam (2009) analyzed a numerical model of a tunnel kiln to fire tiles. The approach of these studies is similar to the one selected for this research. Nevertheless, the behavior of the kilns and the fluid dynamics are quite different since the flows are more complex through the sanitary-ware disposition on the carts than it is along the tiles laying on the rolling plates. The model of fluid dynamics and governing equations are more complex. On the other hand, Romero-Flores et al. (2020) studied the uniformity of temperature in a shuttle kiln by analyzing burners’ interaction. This research focuses on the variability of the thermal demand and waste where the novelty lays on.

The thermal consumers in the sanitary-ware production line need to be analyzed as proposed in Cuviella-Suárez et al. (2018). Again, for this research, the study has been carried out in a dynamic model which shows the variability of the thermal demand. In this regard, it is possible to confront thermal production and demand curves to assess the simultaneity of both and the degree of actual recovery potential. This is a novelty in this research.

Furthering the environmental benefits, there is a potential economic profit as shown in Brückner et al. (2015) where the economy of transforming recovered heat into heating or cooling systems is assessed.

In the state of the art to improve efficiency within the sanitary-ware manufacturing, the authors have concluded that the proposed model to improve efficiency and reduce energy consumption is totally a novelty for the sanitary-ware manufacturing process.

CO2 emissions are reduced since required fuel is cut down. Global requirements regarding climate change and sustainability are therefore accomplished, helping the companies to improve the environmental performance. Additionally, the sustainability is reinforced by means of a more society and people friendly environment, from a health perspective (Monfort et al., 2014).

This research aims to provide a generalized methodology to quantify the savings through a sequence of heat-recovering techniques that progressively improves the thermal energy consumption of the factory (Goldemberg, 1994). Simulation of the factory from the consumption perspective is a novel way to approach the sanitary-ware industry and its sustainability. Some other fields have been approached in similar way (Seferlis et al., 2015) and (L. Wang, 2014).

This methodology, extendible to any industrial facility where thermal consumption at different thermal levels is present, is particularly applied to the sanitary-ware industry. A proper energy management should consider this technique in any field where thermal power is demanded and wasted (Johansson, 2015).

Figure 1 shows the general scheme for thermal consumer equipment usually fed with NG.

Fig. 1
figure 1

Thermal consumer scheme

Full size image

It can be seen that recoverable heat from one consumer could be profited into another consumer. Some industrial processes demand a thermal level which can be provided with recovered heat from a consumer with a higher thermal level (Delpech et al., 2017). The exhausting flow from it is characterized by m and T. This is not a new concept. The real novelty is the methodology to, gradually, apply it to an industrial process where this thermal staggering is driving the production.

The starting point of the research is the energy map of the factory to set the energy consumption pattern (Sathitbun-anan et al., 2014). From this point, this research states the different stages to progressively reduce the thermal requirement by means of a physical and mathematical model; it quantifies the energy reduction in each stage and finally proves that 44% of the energy may be reduced.

The methodology for the progressive application of thermal engineering is as follows:

  • Thermal consumption of conventional factories is quantified with no heat recovery.

  • Then, residual heat from kilns is re-conducted towards heat consumers with lower thermal level as dryers, heating units, or boilers. Pre-heating combustion air of kilns is as well considered, which reduces their NG consumption (Mezquita et al., 2014). On the other hand, less air for combustion is needed which derives a better efficiency (Shiralkar et al., 2014). The BAT guide for the sector of ceramics (BAT CER BREF-EU, 2007) in its Sect. 4.1.2. states the recommendation of recovering heat from kilns for drying processes. Nevertheless, it does not mention the use of this waste heat to pre-heat combustion and secondary inlet air into the kiln as it is suggested in this research as a novelty. However, some providers start to offer pre-heating systems, although this is not yet a standard.

  • The BAT guide for the sector of ceramics (BAT CER BREF-EU, 2007) in its Sect. 4.1.2. states as well that heat recovery from kilns has to be used with simultaneous demand.

Applicability

Recovery of excess heat from kilns, especially from their cooling zones in the form of hot air, can, in principle, be applied in all ceramic sectors to heat dryers. It should be noted, that recovery of excess heat from kilns is only applicable if the excess heat is needed at the same time in another process. The specific example mentioned above (in Germany only very few factories use this technique) cannot be generalized, especially regarding the utilization of the excess heat of the afterburner, because often the flue-gas from an afterburner is too cold to carry out efficient energy recovery.

In this research, the approach tackles the possibility of storing the heat so as the ability to compute simultaneity of recovery-demand to extend the technology to any production facility.

  • Since a conventional factory is run in shifts of 8 h, most of the continuous residual heat from kilns is lost. In order to match heat recovery with thermal requirement and flat the thermal demand curve, the cycles of consumers are extended beyond the standard shift through the whole day long (24 h).

  • Although consumption is improved by flattening the thermal demand curve, it can be further improved by storing heat from periods of heat excess to be used during periods of heat defect.

  • Sustainability is beyond a concept. It is a necessity for the economy to survive the current climate crisis and a critical target for the companies to compete in a more ruled background where efficiency must be strongly improved. In this context, the ceramic sector has to contribute to reducing pressure on natural resources. Companies must develop a culture of saving energy and materials in their operations, by significantly reducing harmful emissions, evolving towards a low-carbon society, and providing efficient use of resources and clean energy (Cuviella-Suárez et al., 2019). A life cycle assessment is a useful tool for a qualitative and quantitative check of consumption. This approach will not only reduce pollution but also make the surviving companies more competitive. Silvestri et al. (2020) analyzed a case study in Italy and Lv et al. (2019) in China.

  • Harder environmental standards affect directly the cost and profitability of the businesses and set the survival of the companies. Resources and technical standards are becoming key factors of performance.

    As the final conclusion after the reviewed literature, it can be stated that this research fills a gap in the state of the art through a modeled procedure to improve efficiency and reduce energy consumption, providing a more sustainable process for sanitary-ware manufacturing.

Experimental

The starting point for this research is the thermal configuration of the two main types of sanitary-ware factories described in Cuviella-Suárez et al. (2018) which is shown in Fig. 2.

Fig. 2
figure 2

Thermal powers of cycle for a sanitary-ware factory

Full size image

The mathematical model of a tunnel kiln was set in Cuviella-Suárez et al. (2018). A similar model has been carried out in this research for the shuttle kiln considering the fluid dynamics throughout the complexity of the sanitary ware which is far different to that of the flat tiles. Here lies the novelty of this model. Simulating the results for both kilns are shown in Fig. 3.

Fig. 3
figure 3

NG requirement for the kilns and potential heat recovery for the kilns. a Tunnel kiln. b Shuttle kiln

Full size image

On the other hand, Fig. 4 shows the thermal requirement of thermal consumers within a sanitary-ware factory, either by plaster or resin molds. These consumers are modeled as per Cuviella-Suárez et al. (2018). They are not influenced by external climate conditions, so they have been considered invariable along the year.

Fig. 4
figure 4

Thermal requirement of different consumers within the factory. a Ware dryer operated in 1 shift. b Ware dryer operated in 2 shifts. c Mold dryer. d Boilers

Full size image

The ware dryer can be operated in one or two cycles. Thus, the required power may be reduced along the daily cycle. On the other hand, mold dryer and boilers can be considered as a constant power, since they are operating under the same basis during the whole cycle.

The heating and ventilation units (HVU’s) are more likely to be influenced by climate conditions: temperature, relative humidity, and solar irradiance. That variability may affect the behavior of the system, so calculations have been made for a whole year in periods of 30 min as per available climate database. These data have been computed and Figs. 5, 6, and 7 show the results. Variability of the daily cycle through the whole year is shown as the gap range between extreme data. Average is also shown.

Fig. 5
figure 5

Variability of ambient temperature

Full size image
Fig. 6
figure 6

Variability of relative humidity of ambient air

Full size image
Fig. 7
figure 7

Variability of the solar irradiance

Full size image

Temperature outside varies from about 0° in winter up to 30° in summer. On an average day, it is between 15° and 20°.

Also, for relative humidity, it ranges from 0.2 in a dry day up to 1 in a wet day, with an average day which ranges within 0.6 to 0.8.

Solar radiation is very poor in a clouded winter day, while it reaches up to 1000 W/m2 at noon in a sunny day.

Climate data have been statistically analyzed for the whole year. Relevant values are those related to involved mentioned variables. The distribution function of temperature along the whole year is shown in Fig. 8.

Fig. 8
figure 8

Distribution function of temperature

Full size image

The shape does not suggest a normal distribution. When aggregated by classes, temperature histogram shows a shape more likely linked to a normal shape as shown in Fig. 9.

Fig. 9
figure 9

Distribution function of temperature aggregated by classes

Full size image

In a similar way, it has produced statistical analysis of relative humidity and solar irradiance, as shown in Figs. 10 and 11.

Fig. 10
figure 10

Distribution function of relative humidity

Full size image
Fig. 11
figure 11

Distribution function of solar irradiance

Full size image

Uncertainty interval for every variable is shown in Table 1.

Table 1 Mean, standard deviation, and confidence interval for climate variables
Full size table

Energy calculations may be carried out with these average values and associated uncertainty. However, they have been achieved for every single period along the year in order to assess the corresponding uncertainty of those results.

As mentioned previously, HVU’s are affected by these uncertainties. Figure 12 shows the daily cycles for both factory heating requirements. The statistical analysis has recorded maximum, minimum, and average thermal power for a cycle of 1 day.

Fig. 12
figure 12

Minimum, maximum, and average thermal power along one daily cycle for HVU’s. a Plaster mold factory. b Resin mold factory

Full size image

By adding thermal powers for every consumer of NG, the demand curve of NG for the two types of factory can be obtained, as shown in Fig. 13. It can be seen that the base curve at night is led by the tunnel kiln. At midday, the shape of dryers and shuttle kiln are clearly identified.

Fig. 13
figure 13

Minimum, maximum, and average thermal power along one daily cycle for conventional factories. a Plaster mold factory. b Resin mold factory

Full size image

It can be seen how climate conditions influence the results. However, the influence is relatively less important than it appears for the HVU’s curves since there are much other power which is not affected by climate.

From Fig. 2, it can be deduced that averaged cycle powers would allow the recoverable heat from kilns to supply the rest of thermal consumers. However, when displayed along the cycles, the variation of the powers does not match. Thus, much power could not be recovered unless heat storage would be added. During some periods, the recoverable heat is greater than the thermal requirement and the difference would be lost. On the opposite, for the rest of the periods, the recoverable heat would not be able to supply the thermal requirement and NG would be needed. Figure 14 shows this fact.

Fig. 14
figure 14

Residual heat from kilns versus thermal demand in other consumers. a Plaster mold factory. b Resin mold factory

Full size image

It can be seen how, theoretically, the residual heat from the exhausting pipes of the kiln may provide thermal power for the rest of equipment.

As already mentioned, kiln inlet airs may be pre-heated in order to reduce the required energy. Less NG is required to operate the kilns. On the other hand, less residual heat is available for the rest of consumers. Pre-heated kilns features are shown in Fig. 15.

Fig. 15
figure 15

Residual heat from kilns versus NG requirement after pre-heating kiln air inlets. a Tunnel kiln. b Shuttle kiln

Full size image

When applying the new capacity of residual heat to the rest of consumers, the availability is not enough to supply them as shown in Fig. 16.

Fig. 16
figure 16

Residual heat from kilns versus thermal demand in other consumers. a Plaster mold factory. b Resin mold factory

Full size image

There is a clear lack of recovered heat to supply the rest of consumers in a PMF. Regarding a RMF, there are two different subperiods identified by either lack or excess of residual heat. In order to flatten the demand curve, the shifts are split in order to reduce peaks of thermal demand. Also, there is a chance of recovering the heat from one period to the other when it is required.

On the other hand, the consumption of the kilns notably reduced. Figure 17 shows the proposed configuration of heat recovery.

Fig. 17
figure 17

Configuration of heat-recovering system

Full size image

Calculation

In the same line that tunnel kiln model was approached in Cuviella-Suárez et al. (2018), the shuttle kiln has been modeled according to the following procedure. To simulate or model the kiln, it has been conceived as a box enclosed by refractory blocks and the cart carrying the ware, as shown in Fig. 18.

Fig. 18
figure 18

Shuttle kiln cross-section

Full size image

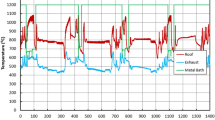
Figure 19 shows the temperature inside the chamber for the complete cycle.

Fig. 19
figure 19

Shuttle kiln temperature curve

Full size image

There are different air flows into the kilns in order to help it to adjust the set curve:

  • Combustion air to produce the oxidization of the NG as per the stoichiometric ratio.

  • Excess of air is set 10% of the combustion air and allows complete combustion.

  • Injection air to be blown to rapidly adjust the excesses of temperature.

  • Diffusion/cooling air to provide uniformity of temperature through the kiln chamber during heating process and cooling the chamber after heating peak.

The mass balance equals the air inlets (combustion, excess, injection, diffusion, and cooling airs), the natural gas mass inlet, and air outlets (exhausted gases and exhausted cooling airs).

$${\sum}_{\mathrm{in}}{\dot{m}}_{\mathrm{in}}={\sum}_{\mathrm{out}}{\dot{m}}_{\mathrm{out}}$$
(1)

On the other hand, the energy balance equals the thermal inlet energies and the sum of outlet energies and losses. Every term of the equation is calculated by multiplying the mass flow by the enthalpy of it at the corresponding temperature, as shown in Eq. (2):

$$\sum_{\mathrm{in}}{\dot{m}}_{\mathrm{in}}{h}_{\mathrm{in}}=\sum_{o}{\dot{m}}_{\mathrm{out}}{h}_{\mathrm{out}}{+W}_{\mathrm{losses}}$$
(2)

Losses are calculated considering thermal transference from inside the kiln to outside including the three components of the heat transference: conduction, convection, and radiation.

Following the stated models, the thermal powers of each cycle are computed over a period of 24 h.

Tunnel kiln is run in permanent regime basis. Thus, recoverable heat from it has been considered as constant. It equals:

$${Q}_{{TK}_{\mathrm{recoverable}}}={Q}_{\mathrm{ex}}+{Q}_{\mathrm{rc}}+{Q}_{\mathrm{sc}}$$
(3)

Rapid cooling air flow is less than combustion air, so the difference to pre-heat the combustion air is supplied by the exhausting flow. Then, pre-heating power for combustion air is obtained by:

$${Q}_{{\mathrm{TK}}_{\mathrm{ca}}}={{\dot{m}}_{\mathrm{ca}}\cdot C}_{{p}_{\mathrm{air}}}\cdot \left({T}_{\mathrm{ca}}-{T}_{0}\right)$$
(4)

where

$${T}_{\mathrm{ca}}=\frac{{\dot{m}}_{\mathrm{rc}}\cdot {T}_{\mathrm{rc}}+\left({\dot{m}}_{\mathrm{ca}}-{\dot{m}}_{\mathrm{rc}}\right)\cdot {T}_{\mathrm{ex}}}{{\dot{m}}_{\mathrm{ca}}}$$
(5)

Shuttle kiln firing cycle from cold to cold is repeated every day, so thermal power varies during the cycle. However, the way to calculate the power for any period of the cycle is similar to the tunnel kiln with the only difference that there is just one exhausting flow and temperature.

$${Q}_{{\mathrm{SK}}_{\mathrm{recoverable}}}={Q}_{\mathrm{ex}}$$
(6)
$${Q}_{{\mathrm{SK}}_{\mathrm{ca}}}={{\dot{m}}_{\mathrm{ca}}\cdot C}_{{p}_{\mathrm{air}}}\cdot \left({T}_{\mathrm{ex}}-{T}_{0}\right)$$
(7)

Then, residual recoverable heat after pre-heating the combustion airs equals:

$${Q}_{\mathrm{recovered}}={Q}_{{\mathrm{TK}}_{\mathrm{recoverable}}}-{Q}_{{\mathrm{TK}}_{\mathrm{ca}}}+{Q}_{{\mathrm{SK}}_{\mathrm{recoverable}}}-{Q}_{{\mathrm{SK}}_{\mathrm{ca}}}$$
(8)

The thermal demand in every period is the sum of HVU’s, ware-dryers, and mold dryers or boilers depending on the type of factory.

$${Q}_{\mathrm{demand}}={Q}_{\mathrm{HVU}\prime \mathrm{s}}+{Q}_{\mathrm{ware}-\mathrm{dryers}}+{Q}_{\mathrm{mold}-\mathrm{dryers}}\kern0.5em \left(\mathrm{for}\ \mathrm{plaster}\ \mathrm{mold}\ \mathrm{factories}\right)$$
(9)
$${Q}_{\mathrm{demand}}={Q}_{\mathrm{HVU}\prime \mathrm{s}}+{Q}_{\mathrm{ware}-\mathrm{dryers}}+{Q}_{\mathrm{boilers}}\kern0.5em \left(\mathrm{for}\ \mathrm{resin}\ \mathrm{mold}\ \mathrm{factories}\right)$$
(10)

To compute the NG power for the thermal demand required in each period,

$${Q}_{{\mathrm{NG}}_{\mathrm{demand}}}={Q}_{\mathrm{demand}}-{Q}_{\mathrm{recovered}}$$
(11)

When \({Q}_{{\mathrm{NG}}_{\mathrm{demand}}}\) results in positive, there is a lack of heat to be supplied with NG. When it results in negative, the excess heat is lost or stored for next periods of lacking heat.

The total power of NG required for the factory is the sum of the demand plus the kilns:

$${Q}_{{\mathrm{NG}}_{\mathrm{factory}}}={Q}_{{\mathrm{NG}}_{\mathrm{demand}}}+{Q}_{{\mathrm{NG}}_{\mathrm{kilns}}}$$
(12)

When this power is averaged for the whole day (48 periods of 30 min), the savings of NG can be computed and compared to each other.

$${\overline{Q}}_{{\mathrm{NG}}_{\mathrm{factory}}}=\frac{\sum_{i=1}^{48}{{Q}_{{\mathrm{NG}}_{\mathrm{factory}}}}_{i}\cdot {t}_{i}}{\sum_{i=1}^{48}{t}_{i}}$$
(13)

This averaged power is computed for every configuration:

  • Conventional factory plaster molds

  • Conventional factory resin molds

  • Optimized factory plaster molds

  • Optimized factory resin molds

Results

After flattening the curve of demand and recovering residual heat, there is a net reduction of energy consumption. Figure 20 shows the results obtained for comparison between conventional and optimized factories, so as for plaster or resin mold ones.

Fig. 20
figure 20

Energy savings after factory optimization. a Plaster mold factory. b Resin mold factory

Full size image

Corresponding thermal powers are detailed in Table 2.

Table 2 Absolute and relative energy savings for a daily cycle from a CF
Full size table

These savings show the highest improvement that can be achieved between the extremal configurations (CF and OF). However, it may happen that a factory operates with already improved kilns that incorporate pre-heating of the inlet airs. In such case, the efficiency increase would not be so great, though there would be some improvement by heat recovery. Such configuration has been set as pre-heated factory (PHF). Figure 21 and Table 3 show the results for this case.

Fig. 21
figure 21

Energy savings by recovering heat in a pre-heated factory. a Plaster mold factory. b Resin mold factory

Full size image
Table 3 Absolute and relative energy savings for a daily cycle from a PH factory
Full size table

For the relevant influence of climate variables in the energy consumption, finding a multivariable correlation by means of an artificial neural network (ANN) has been tried. However, due to other important factors as the discontinuity of the operation set points for the equipment, it could not be adjusted with an acceptable error margin. Figure 22 shows the proposed ANN.

Fig. 22
figure 22

ANN to correlate climate variables with required energy

Full size image

On the other hand, a series of single correlations has been tried as shown in Fig. 23.

Fig. 23
figure 23

Temperature, humidity, and irradiance regressions of the consumed energy of the factory

Full size image

A polynomial of second degree has been computed by least square adjustment, whose parameters can be seen in Fig. 23 as well.

Since regression tries have not been accurate enough to represent the consumed energy, a statistical analysis of the energy itself for each factory configuration also has been achieved, as seen in Fig. 24.

Fig. 24
figure 24

Density function of consumed energy distributions. a CF of plaster molds. b CF of resin molds. c OF of plaster mold. d OF of resin molds

Full size image

The uncertainty analysis states the confident intervals of the expected energy as per Table 4.

Table 4 Mean, standard deviation, and confidence interval for energy requirement of the four configurations
Full size table

As a key factor on the energy consumption, the production has been also analyzed. The result of it is shown in Fig. 25. The required energy is linear with the production, though there is a fixed consumption for any configuration including losses through the walls of the equipment, heat required by carts, supports, refractory, etc.

Fig. 25
figure 25

Sensitivity analysis of the energy consumption in respect to production. a Plaster mold factory. b Resin mold factory

Full size image

Discussion

From Figs. 2 and 17, it can be deduced that recovered heat from kilns might supply the rest of the thermal consumers. However, these are average values. The behavior of the equipment is different through the daily cycle as seen in Figs. 3, 4, and 12, so as the thermal requirement for them. Additionally, there is a seasonal difference of operation for HVU’s as shown in Fig. 12 due to climate influence. Under such circumstances, averaged values may lead to unclear results. The uncertainty of these results is defined by these variables and their ranges of variation. Figures 5, 6, and 7 show the variation of the climate factors along the year. In order to work with the mean of the values, the uncertainty of the climate values which has to be transferred to the expected results regarding energy has been defined, in Table 1. Figures 8, 9, 10, and 11 show the statistical analysis of the climate values and their functions of probability distribution. The shape of the curves and the variation range of temperature, humidity, and solar irradiance is clearly identified in Fig. 12 where the HVU thermal requirement is analyzed. The seasonal and daily difference between cold and warm days can be seen. The maximum and minimum thermal requirements corresponding to cold and warm day respectively can be identified. On the other hand, there is a decrease of thermal requirement in the midday when there is higher temperature and solar irradiance. This effect is greater for the PMF due to higher requirement during night time. In Fig. 13, the effect is less visible because it is diminished by the rest of thermal consumers which do not depend on the external conditions. Besides, the PMF shows a slightly greater range from cold to warm day than the RMF since the relative influence of HVU which is more important in the former.

Potential reduction of NG is clearly identified in Figs. 14 and 16. Figure 14 shows how the recovered heat from conventional kilns may supply the rest of thermal consumers as Fig. 2 suggested. However, when the kiln is optimized by recovering heat backwards, there is a lack of heat for the rest of consumers as shown in Fig. 17 in average terms. Nevertheless, when analyzing the whole cycle, it can be seen how there are periods of excess and lack of heat as shown in Fig. 16. This effect is more pronounced for the PMF where the HVU demands a greater amount of energy to dry molds during night time.

After analyzing the potential of heat recovery through the whole cycle and the uncertainty of the different variables affecting it, Fig. 20 shows the total NG savings when a CF is optimized by recovering heat from kilns. Table 2 defines the corresponding values for a daily cycle stating that 44% of potential saving is achievable. Even in the event of a partially optimized PHF, it is feasible to reach some NG reduction which may result in 22% for a PMF and 16% for a RMF. Though these values have been computed through the whole-year cycles, they have been statistically averaged with an uncertainty which can be seen in Table 4. Figure 24 shows the probability distribution function of the resultant thermal energy required for each configuration. The optimized factory shows a shape closer to a normal distribution. It is due to the effect of the steadier supply from heat recovery. Conventional factory is more subjected to the climate effects. Thus, more dispersion can be appreciated.

Multivariate correlation ANN has failed because of a great discontinuity of energy as a function of temperature, humidity, irradiance, and set point periods. The error by least square adjustment is not acceptable. On the other hand, the single correlations appear quite well adjusted as can be seen in Fig. 23. They have resulted in quite accurate for the RMF because there is no discontinuity from day to night as it happens in the PMF which shows a greater dependence on the humidity and irradiance which are quite more disperse than temperature.

From the production point of view, the dependence is basically linear as it can be seen in Fig. 25. There is a fixed energy base and then a linear increase with the production. This base is greater in the PMF due to the HVU demand.

Conclusions

This research has stated the direct dependence of the required thermal energy on the climate factors. A harsher climate produces a higher thermal demand due to lower temperature average and annual solar irradiance. The dependence on the humidity is less direct. A humid environment produces a higher volume of air to be heated in order to extract the water from ware and molds.

On the other hand, it has been concluded that required energy is directly proportional to production.

The uncertainty of the climate factors is reflected on the required energy levels whose intervals of confidence have been assessed.

Correlations between uncertainty factors and resultant energies have been tried and it has been found that there is an acceptable relation between single dependences of the climate variables and resultant energy. However, multivariable correlation has failed.

With regard to net savings, it has been concluded that heat recovery derives an energy saving for any configuration of either conventional factory or improved factory by pre-heating kiln inlet airs. Forty-four percent of NG saved for the former and 22% or 16% respectively from PMF and RMF when kiln inlet air is pre-heated.

The “Introduction” Section stated the need of an analysis of heat recovery potential within this industrial sector. This paper has contributed to this aim assessing the scope of the potential reduction of resources and the possibility to extend the technology to any ceramic factory regardless of the simultaneity of the production–demand curves. Besides, this research furthers the achievement in Cuviella-Suárez et al. (2018) regarding the energy efficiency of an intensive field of the industry.

The scope of the research does not include electrical or water analysis. Thus, it may be a challenge to make a similar and complementary study for these variables in order to enlarge the resource reduction.

On the other hand, only heating or drying processes have been taken into account in this research. However, other uses of recovered heat may be considered, such as distillation or absorption, in order to improve the global efficiency.