Introduction

A fundamental change in the supply of energy is observable worldwide, as demonstrated by the following examples. The United Nations Framework Convention on Climate Change (UN-FCCC) calls for an 80–95% reduction of greenhouse gases over 1990 across all sectors by 2050 (United Nations Framework Convention in Climate Change 2017). In keeping with the New Zealand Energy Strategy 2011–2–21, New Zealand has set itself the goal of providing 90% of its electricity from sustainable energy sources by 2025 (Ministry of Economic Development New Zealand 2011). In 2013, the United Kingdom (UK) introduced the Carbon Price Floor, which taxes fossil energy sources, thus promoting investments in renewables. Furthermore, the UK announced in 2015 that the generation of energy from coal without carbon capture and storage will be restricted from 2023 onward and phased out by 2025 (Hirst 2018). The German Renewable Energy Sources Act stipulates that 80% of electricity must be supplied by renewable energy sources by 2050 (Erneuerbare-Energien-Gesetz 2017).

Given the high volatility of renewable energy sources, changes in the electricity sector are concomitant with substantial difficulties in terms of demand responsiveness. A drastic reduction of greenhouse gas emissions will require the decarbonization of all energy sources in Germany. This will create additional challenges that will particularly affect the sectors responsible for a large part of greenhouse gas emissions, namely electricity, heat, and transportation (Umweltbundesamt (2020)).

The 755 million tons of carbon dioxide emitted in Germany in 2018 are broken down by sector in Fig. 1 (Umweltbundesamt (2020)).

Fig. 1
figure 1

Carbon dioxide emissions in Germany (2018, percentage breakdown of 755 million tons) (based on (Umweltbundesamt (2020)))

Full size image

The energy supply sector (electricity and heat) currently emits the most carbon dioxide. Since this sector only accounts for 56% (Umweltbundesamt (2020)) of total carbon dioxide emissions, decarbonizing the energy sector alone will not suffice to comply with international climate agreements. Complying with future regulations will require extending decarbonization to the transportation, industrial, and private sectors. Figure 1 shows that the transportation and household sectors account for a significant share of carbon dioxide emissions and therefore must be factored into optimization approaches.

Several power-to-X (P2X) technologies utilize renewable energies to reduce greenhouse gases across all sectors, making them ideal technologies for meeting the aforementioned regulations (e.g., the Paris Agreement and the German 2017 Renewable Energy Sources Act) (Schenuit et al. 2016).

Commercial use of P2X is nevertheless a topic of debate (Urbansky 2017; Dämgen 2018; Grünewald 2019). Efficiency factors presented in the literature lack repeat accuracy at times and differ greatly from each another in some cases (Koj et al. 2019). As a result, evaluations of P2X technologies are not always fully convincing, even when based on life cycle assessments, and may even reveal disadvantages compared with conventional technologies (Ausfelder and Dura 2018; Koj et al. 2019).

The evaluation of energy efficiency is an important element of the achievement of the ambitious political goals and the commercialization of new technologies (Pehnt 2011). The methodical evaluation of energy efficiency specified by regulations and guidelines facilitates the development of transparent and unified indicators. The newly introduced VDI Guideline 4663, which provides a methodology for the evaluation of energy performance indicators based on limit values, ought to be applicable to renewable energies and their concepts too. A key element of this guideline is the physical optimum (PhO), a novel, promising energy indicator that appears well suited for the evaluation of efficiency and the optimization of (P2X) processes.

This study applies the PhO to a power-to-gas (P2G) process to enable a unified comparison of P2X technologies with conventional energy conversion and storage measures, even in terms of political goals. “Power-to-gas applications” presents common P2G applications to elucidate the evaluated processes. “The physical optimum as a universal method for process evaluation” introduces the PhO as a limit value, and “Fundamentals of power-to-methane” presents the fundamentals of power-to-methane for the subsequent evaluation of an essential process component, a heat exchanger, in “Process optimization with VDI 4663.” Finally, “Conclusion and outlook” describes the targeted process optimization based on VDI guideline 4663.

Power-to-gas applications

Power-to-gas introduced the cross-sectoral use of renewable energy to discourse (Sterner 2017a). This approach uses electricity from renewable sources to operate an electrolysis cell. The hydrogen produced can either be stored for use or methanated by adding carbon dioxide. The power-to-methane process chain thus enables connecting the electricity sector to the natural gas grid.

This section summarizes the fundamentals of hydrogen production, methanation technology, and current P2G implementation that are essential to understanding the significance of the evaluation project and the application of the PhO method.

Technical fundamentals of hydrogen production

P2G usually produces hydrogen by water electrolysis, making this the most important step for P2G and P2X applications technologically. Water electrolysis is an established and well understood technology. Developments in fuel cell technology have been instrumental in advances in water electrolysis (Götz et al. 2016). The process of water electrolysis is based on an electrochemical reaction that splits water into its chemical components. The direct current and voltage applied to water or steam splits it into hydrogen (H2) and oxygen (O2).

An electrolysis cell consists of two conductive metal electrodes (anode and cathode) separated by an electrolyte. Electrolysis cells assembled in stacks are often connected in series in electrolyzer plants where auxiliary devices (e.g., electrical control systems and water treatment and hydrogen handling equipment) control the plant (Decourt, 2019).

Three different electrolysis technologies are particularly interesting for P2G chains: alkaline electrolysis, polymer electrode membranes, and solid oxide electrolysis (Götz et al. 2016). A variety of detailed research and review data on the types of electrolysis for P2G applications are available in the literature (e.g., Wulf, Linssen, Zapp, 2018; Gahleitner, 2013; Götz et al., 2016).

Ongoing research and development are exploring additional processes for the production of hydrogen based on renewable energy sources, e.g., coelectrolysis of syngas (a mixture of hydrogen and carbon monoxide) (Leitner et al. 2018) and the production biogenic hydrogen by dark fermentation (Show et al 2019).

Methanation processes

When P2G is treated as an electrochemical energy storage technology, injection criteria limit the extent to which electrolytically produced hydrogen can be injected into the natural gas grid (Eckert, Sterner, Thema, 2017). This makes subsequent methanation of hydrogen to increase P2G storage capacity and expand sector coupling particularly attractive in regions with extensive natural gas infrastructures (Ghaib, 2017).

Different processes can be employed to produce methane in P2G. The methanation of hydrogen can be catalyzed both biologically and chemically. The Fischer–Tropsch process can be used to methanate the syngas produced by coelectrolysis. Moreover, other technical processes employing various intermediate steps or the use of the methane produced during biomass-gasification or fermentation are conceivable.

A variety of detailed research and review data on the methanation processes for P2G applications are available in the literature (e.g., Eckert, Sterner, Thema, 2017; Frick et al., 2014; Gahleitner 2013).

Capabilities and pathways of power-to-gas technologies

Since the European power grid lacks sufficient storage capacity, P2G offers the capability to store electricity expediently in the natural gas grid as chemical energy (Gahleitner 2013). Whereas the total global storage capacity is over 3600 TWh for natural gas (Wallbrecht 2006), it was only 639 TWh for wind and solar electricity in 2012 (Observ’ER 2013).

Numerous P2G plants have been built or are in planning all over the world (Gahleitner 2013; Wulf, Linssen, Zapp 2018). European plants have a maximum capacity of 9.4 to 15,000 kW (Wulf, Linssen, Zapp 2018).

P2G technology is now more expansive, comprising more than just water electrolysis as the first step of the process. Hydrogen remains the main (intermediate) product, though. The various potential uses of hydrogen and methane are spawning opportunities for coupling the electricity, heat, and transportation sectors and even the chemical industry. The P2G process has been steadily expanded into P2X (Wulf, Linssen, Zapp 2018).

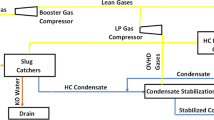
Figure 2 presents examples of P2X applications’ most important pathways but does not describe every single option for P2X process interfacing.

Fig. 2
figure 2

The most important power-to-X pathways (based on (Sterner 2017a; Bünger et al., 2017))

Full size image

Given the wide variety of P2X applications, this paper primarily focuses on the power-to-methane process. The authors intend to evaluate the efficiency of other P2X process chains in the very near future.

The physical optimum as a universal method for process evaluation

Conventional methods for evaluating P2G processes often deliver poor results, frequently resulting in the evaluated processes being designated “too expensive” (Dämgen 2018) or “too inefficient” (Urbansky 2017).

The power-to-methane process evaluated by Viktor, Schabbach, Link, and Fischer (2017), for instance, has an overall efficiency of 56%, while other sources cite overall efficiencies of 46 to 68% for the same process (Viktor, Schabbach, Link Fischer 2017; Müller-Syring 2011; Zukunft ERDGAS GmbH 2017). The power-to-hydrogen process, on the other hand, has a slightly better efficiency of about 54 to 77% (Allelein and Zahoransky 2015; Sterner et al. 2011). The problem with conventional process evaluation, however, is the use of ideal comparative processes as benchmarks, resulting in misleading efficiency indicators. The maximum efficiency achievable of 100% implies that all losses can be eliminated by optimizing a process, something equivalent to a perpetual motion machine of the first kind. Since this does not represent the limit of optimization actually achievable, the capability to optimize a process is not ascertainable with conventional evaluation methods.

This problem is nothing new. Although many evaluation methods and performance indicators for the estimation of optimization capability exist, they are usually for specific industries or even processes and thus frequently dependent on the state of the art and cannot be applied across sectors.

Since P2G processes represent a technology for sector coupling, a cross-sectoral method for the evaluation of partial and complete processes that establishes the limits of optimization, regardless of the state of the art, is required.

This challenge could be met with the PhO, which was defined by Volta and represents an ideal theoretical reference process incorporating all scientific laws. This reference process, which cannot be improved any further, constitutes the maximum optimization capability. Since conventional reference processes and thermodynamic cycles do not factor in a process’s maximum operational capability under physically optimal conditions, they only permit improvement, but never optimization (Volta 2014).

Since the PhO is an ultimate reference point not based on the best technology available and is time-independent as long as the laws of physics are incorporated, energy indicators cannot be revised continuously, as is currently observable in electric motors or household appliances (Fig. 3) (Volta 2014).

Fig. 3
figure 3

Revision of the electric motor efficiency classes introduced in 1998 by the European Committee of Manufacturers of Electrical Machines and Power Electronics (EFF standing for efficiency). The efficiency classes defined by the standard EN 60,034–30:2009 have been applied worldwide since 2009 (IE standing for International Efficiency) (based on Volta (2014))

Full size image

The biggest challenge in determining the ultimate reference process is establishing the amount of work to run the process that is unavoidable even when optimized. Since this part of the energy is unusable, it must be analyzed separately in the evaluation. The unusable part of the energy must be defined as an unavoidable loss in order to be able to use a key indicator to draw conclusions about the optimization capability to evaluate processes. Energy conversion in a wind turbine during which the wind’s kinetic energy is transformed into the rotor’s rotational energy is an example of a process with unavoidable losses. Part of the wind’s energy flowing through a rotor is captured and the wind is slowed to around one-third of its initial speed. Ideally, slowing the wind down to 0 m/s would maximize the energy yield but this would halt the process since the air would cease flowing. The Betz factor (cp,Betz = 0.593) defines the physical limit of a wind turbine’s energy conversion process as well as the unavoidable losses (1 − cp,Betz = 0.407). Factoring the unavoidable losses into the formulation of the PhO factor (FPhO) produces a key indicator between 0 and 1 that denotes the optimization capability.

The PhO factor can be employed to modify common tools such as Pareto charts or energy loss cascades for use in the targeted optimization of technical processes. Volta also developed new tools, such as capability analysis.

Keichel rendered the method applicable for a wide range of users by introducing the consumption and demand perspective. Supply processes are evaluated using the consumption perspective. Steam generators, for instance, use air, combustibles, and water to produce steam at a certain pressure and temperature. The PhO factor of such processes is defined by the energy supplied in real terms (output) and the energy supplied under physically optimal conditions (PhO input) (Keichel 2017). The demand perspective describes processes that require resources to run. Since pumps or fans, for instance, require electricity to produce a pressure difference in a fluid flow, they are evaluated from the demand perspective, which is defined by the energy required by the process in real terms (input) and the energy required under physically optimal conditions (PhO output) (Keichel 2017). The following figure visualizes the definitions of the perspectives (Fig. 4).

Fig. 4
figure 4

The two different perspectives employed in the PhO method (based on Keichel (2017))

Full size image

The consumption perspective and its limit are defined as follows:

$${\mathrm{F}}_{\mathrm{PhO}}^{\mathrm{V}}=\frac{\mathrm{Output}}{\mathrm{Input}\left(\mathrm{PhO}\right)}=\frac{\mathrm{V}}{{\mathrm{V}}_{\mathrm{PhO}}}\le 1$$
(1)

The demand perspective and its limit are defined as follows:

$${F}_{{PhO}}^{B}=\frac{{Input}}{{Output}\left({PhO}\right)}=\frac{B}{{B}_{{PhO}}}\ge 1$$
(2)

A variety of process steps normally contribute to overall efficiency of evaluated industrial processes. In such a case, the PhO factors have to be combined to produce an overall factor that defines the process’s maximum optimization capability. The following equation couples a consumption process with a demand process (Keichel 2017):

$${F}_{{PhO}}^{{ges}}=\frac{{F}_{{PhO}}^{B}}{{F}_{{PhO}}^{V}}\ge 1$$
(3)

VDI 4663 furnishes guidelines for evaluating the efficiency of transport processes, e.g., in heat exchangers. Keichel introduced the capacitive perspective for this purpose. It compares the energy that is transferred in real terms with the energy that could be transferred under physically optimal conditions, factoring in actual conditions, such as the device’s structural design (Keichel 2017).

$${F}_{{PhO}}^{K}=\frac{{Q}_{{real}}}{{Q}_{{PhO}}}\le 1$$
(4)

Volta limited his study to the evaluation of processes’ material efficiency and energy consumption. Keichel extended the methods to include instantaneous values as well. Values describing current operating conditions provide information on processes’ current efficiency, thus enabling the identification of inefficient process states and intervention in real time. Moreover, specific processes can be targeted for optimization. The power-based PhO factor is defined by power in real terms and power under physically optimal conditions. It can also be specified by deriving the energy-based PhO factor over time (Keichel 2017):

$${f}_{{PhO}}^{K}=\frac{{\dot{Q}}_{{real}}}{{\dot{Q}}_{{PhO}}}\le 1$$
(5)

Fundamentals of power-to-methane

Extensive process knowledge is required to apply the VDI guideline and the PhO methodology. As explained in “The physical optimum as a universal method for process evaluation,” the complete process must be subdivided into subprocesses before applying the guideline’s individual approaches.

Since a complete evaluation of any P2X application requires an evaluation of all process steps, this study focuses on applying the method to P2G as presented in Fig. 5. Specifically, electrolysis and methanation are examined. Since analyzing the entire power-to-methane chain would require the analysis and partial division of the processes of power generation, electrolysis, carbon dioxide capture, and methanation into new subprocesses, such an analysis would exceed the scope of this paper.

Fig. 5
figure 5

The stages of the power-to-methane process chain examined in this study

Full size image

Electrolysis

A plant’s PhO, including transport losses, is determined by analyzing the minimum energy input required based on the laws of thermodynamics and the real conditions at the plant. The PhO is compared with real measured values to determine the capability to optimize the existing plant’s operation.

The procedure for determining the specific PhO is demonstrated below with a water electrolysis cell as an example. The electrolysis process must be specified beforehand, e.g., as alkaline electrolysis or polymer electrolyte membrane-electrolysis. This permits a comparison of different electrolysis technologies’ physical optima. Since the basic physics do not differ among the technologies, the model described in this section can represent different electrolysis technologies. Model parameters are adjusted to specify the model. The electrolytic composition of water is based on the reaction in Eq. (6) (Pitschak, Mergel, Müller 2017). Water is split into its elements of hydrogen and oxygen by supplying energy equal to the enthalpy of the reaction. Energy must be provided to the process since it is endothermic. According to Keichel, the electrolysis cell must therefore be evaluated from the demand perspective (Keichel 2017).

$${{H}}_{2}{O}+\Delta {{H}}_{{R}}\to {{H}}_{2}+\frac{1}{2}{{O}}_{2}$$
(6)

The first law of thermodynamics states that, disregarding the change in kinetic and potential energy, this chemical reaction’s power of balance is obtained using Eqs. (7)–(9) (Baehr and Kabelac, 2016). The heat (\(Q\)) and electricity required (\({P}_{el}\)) comprise the electrolysis cell’s total energy requirement (\({B}_{{Elektrolyse}}\)). Since this is an electrochemical reaction, a complete conversion of the water is assumed for the PhO (\({\dot{z}}_{{a}}=1\)).

$${B}_{{EElectrolysis}}=\dot{Q}+{P}_{{el}}$$
(7)
$$\dot{Q}+{P}_{{el}}={\dot{z}}_{{a}}{\Delta }^{R}{H}_{{m}}(T,p)$$
(8)
$$\dot{Q}+{P}_{{el}}={\dot{z}}_{{a}}\left({H}_{{m},{{H}}_{2}}\left(T,p\right)+\frac{1}{2}{H}_{{m},{{O}}_{2}}\left(T.p\right)-{H}_{{m},{{H}}_{2}{O}}\left(T,p\right)\right)$$
(9)

According to the second law of thermodynamics, the standard enthalpy of reaction is defined by the amount of energy that must be provided to the reaction as electricity and the maximum amount of thermal energy (\(\dot{Q}\)) (Pitschak, Mergel, Müller 2017). The entropy difference resulting from the standard molar enthalpies of formation (\({H}_{{m},{j}}\)) in Eq. (10) defines the amount of reaction heat. Inserting this in Eq. (8) and rearranging it yields Eq. (11). The free reaction energy (\({\Delta }^{R}{H}_{{m}}(T,p)\)) can consequently be used to calculate the minimum amount of electrical energy required (Eq. (12)) (Pitschak, Mergel, Müller 2017).

$$\dot{Q}= T{\Delta }^{R}{S}_{{m}}\left(T,p\right)-T{\dot{S}}_{{irr}}$$
(10)
$${\Delta }^{R}{H}_{{m}}={\Delta }^{R}{G}_{{m}}\left(T,p\right)+T{\Delta }^{R}{S}_{{m}}\left(T,p\right)$$
(11)
$${P}_{{el},{rev}}={\Delta }^{R}{G}_{{m}}+T{\dot{S}}_{{irr}}={\Delta }^{R}{H}_{{m}}(T,p)-T{\Delta }^{R}{S}_{{m}}\left(T,p\right)+T{\dot{S}}_{{irr}}$$
(12)

The irreversible reaction causes the entropy production flow. Entropy production in the thermodynamically ideal case of a reversible reaction is \({S}_{{irr}}=0\), the amount of electrical energy that must be supplied to the process of water electrolysis corresponding to the molar work of the reversible reaction (Baehr and Kabelac, 2016).

The minimum amount of electricity required to separate one mole of water (or to generate one mole of hydrogen) under standard conditions is given by Eq. (15), factoring in the standard enthalpies of formation (\({H}_{{m},{j}}^{0}\)) (Eq. (13)) and the standard entropies (\({S}_{{m},{j}}^{0}\)) (Eq. (14)).

$${\Delta }^{R}{H}_{{m}}^{0}={H}_{{m},{{H}}_{2}}^{0}+\frac{1}{2}{H}_{{m},{{O}}_{2}}^{0}-{H}_{{m},{{H}}_{2}{O}}^{0}=286.0\frac{{kJ}}{{mol}}$$
(13)
$${\Delta }^{R}{S}_{{m}}^{0}={S}_{{m},{{H}}_{2}}^{0}+\frac{1}{2}{S}_{{m},{{O}}_{2}}^{0}-{S}_{{m},{{H}}_{2}{O}}^{0}\frac{{J}}{{mol}*{K}}=163.1\frac{{J}}{{mol}*{K}}$$
(14)
$${\Delta }^{R}{G}_{{m}}^{0}={\Delta }^{R}{H}_{{m}}^{0}-T{\Delta }^{R}{S}_{{m}}^{0}=237.2\frac{{kJ}}{{mol}}$$
(15)

The decomposition voltage for water electrolysis under standard conditions can be calculated from the free standard reaction energy with Faraday’s laws of electrolysis using Eq. (16).

$${U}_{{rev}}^{0}=\frac{{P}_{{el},{rev}}}{z*F}=\frac{{\Delta }^{R}{G}_{{m}}^{0}}{z*F}=1.23 V$$
(16)

Since the free reaction energy is a function of the operating temperature and pressure, however, different values may result for the cell voltage, as shown in the simplified Nernst equation (Schalenbach et al. 2016).

$${U}_{{rev}}={U}_{{rev}}^{0}-0.000846\frac{V}{K}\left(T-298.15 K\right)+\frac{RT}{2F}{ln}\left(\frac{{p}_{H2}\sqrt{{p}_{{O}_{2}}}}{{p}_{{H}_{2}O}}\right)$$
(17)

If the electrolysis cell operates above ambient temperature, additional thermal energy is required to control the cell temperature. This is disregarded here. The electrolysis cell is assumed to operate under standard conditions.

Resistances, which result from the transient losses and are unavoidable even with optimization, must be factored in in addition to the reversible cell voltage (\({U}_{{rev}}\)). The cell voltage required to dissociate water in the PhO is the sum of electrical resistances in the cell. It is yielded by the decomposition voltage under the given conditions \({U}_{{rev}}\), the kinetically induced overvoltage \({U}_{{Kin}}\), and the ohmic resistances \({U}_{\Omega }\) (cf. Equation (18)) (Schalenbach et al. 2016). The respective summands are defined by Eqs. (17), (19), and (20). The electrolysis cell’s ohmic resistances are calculated factoring in the electrical resistances of the cell’s electrodes \({R}_{{e}}\) and separator \({R}_{{sep}}\). The equation that determines the electrolysis cell’s kinetic overvoltage is an approximation derived from the Butler-Volmer equation and incorporates the Tafel scope \(a\), the current density \(j\), and the exchange current density \({j}_{0}\) (Schalenbach et al., 2016).

$${U}_{{Zell}}={U}_{{rev}}+{U}_{\Omega }+{U}_{{Kin}}$$
(18)
$${U}_{\Omega }=\left({R}_{{e}}+{R}_{{sep}}\right)j$$
(19)
$${U}_{{Kin}}\approx a{ln}\left(\frac{j}{{j}_{0}}\right)$$
(20)

The model parameters required to solve the equations can be determined by taking direct measurements at the plant or by using manufacturers’ data (Schalenbach et al., 2016).

The PhO factor in Eq. (2) is the quotient of the real energy expended and the amount of energy applied under optimal physical conditions. The PhO factor for the energy supplied by electricity in Eq. (21) can be determined from the power and the cell voltage.

$${F}_{{PhO}}^{B}=\frac{{P}_{{real}}}{{P}_{{PhO}}}=\frac{{U}_{{real}}zF}{{U}_{{Pho}}zF}=\frac{{U}_{{real}}}{{U}_{{PhO}}}$$
(21)
$${F}_{{PhO}}^{B}=\frac{{U}_{{real}}}{{U}_{{rev}}+{U}_{\Omega }+{U}_{{Kin}}}$$
(22)
$${F}_{{PhO}}^{B}=\frac{{U}_{{real}}}{{U}_{{rev}}^{0}-0.000846\frac{V}{K}\left(T-298.15 K\right)+\frac{RT}{2F}{ln}\left(\frac{{{p}}_{{H}2}\sqrt{{{p}}_{{{O}}_{2}}}}{{{p}}_{{{H}}_{2}{O}}}\right)}+\frac{{U}_{{real}}}{\left({R}_{{e}}+{R}_{{sep}}\right)j}+\frac{{U}_{{real}}}{a {ln}(\frac{j}{{j}_{0}})}$$
(23)

Conclusions about the extent to which the efficiency of an existing water electrolysis cell could be increased by actions such as cleaning can be drawn based on this PhO factor.

Methanation

Methanation converts hydrogen produced by electrolysis into methane by adding carbon dioxide (Ghaib 2017). The chemical process described by the Sabatier Reaction can be divided into the following partial reactions (Sterner 2017b):

$${{H}}_{2}+{{CO}}_{2}\rightleftharpoons {CO}+{{H}}_{2}{O}$$
(24)
$$\Delta {H}_{{R}}^{0}=41 {kJ mo}{{l}}^{-1}$$
$$3 {{H}}_{2}+{CO}\rightleftharpoons {{CH}}_{4}+{{H}}_{2}{O}$$
(25)
$$\Delta {H}_{{R}}^{0}=-206 {kJ mo}{{l}}^{-1}$$

Since the overall methanation reaction is highly exothermic and has a negative molar balance, it benefits from lower temperatures and high pressures, in keeping with Le Chatelier’s principle (Sterner 2017b).

In addition to methane, the reaction can also produce such by-products as carbon monoxide, carbon, and hydrocarbons (Ghaib 2017).

The choice of operating conditions directly affects the side reactions and the chemical equilibrium. Methanation at maximum pressures and minimum temperatures is most expedient thermodynamically (Ghaib 2017).

The kinetic barrier to the reduction of fully oxidized carbon to methane is very high since it is an eight-electron reaction. Activation energy is required, despite the use of catalysts. The reaction is therefore usually run at about 300 °C (Ghaib 2017).

The greatest challenge of the methanation reaction is releasing the reaction heat efficiently since it is needed to maintain the exothermic reaction’s chemical equilibrium. Heat release must therefore be factored into the evaluation of methanation’s energy efficiency. The evaluation of the efficiency of a heat exchanger’s reaction heat removal is therefore examined separately in Sect. 3.3.

The activation energy applied and the hydrogen and carbon dioxide added must be treated as inputs to evaluate the efficiency of the methanation reaction. Only the pure methane is treated as an output. The quantity of heat recovered by the heat exchanger described in Sect. 3.3 could be incorporated as positive process interfacing to expand use of the PhO method. Since the upstream water electrolysis was analyzed under standard conditions here, the excess reaction heat was disregarded. Co-products and by-products of the methanation reaction must be included in the calculation of the PhO as unavoidable losses.

The activation energy of the methanation reaction can be estimated with the Arrhenius equation. Essentially, for a function of the operating temperature and the catalyst used, it determines the frequency factor \(A\) and the rate constant \({k}_{{i}}\) (Czeslik et al. 2009).

$${k}_{1}=A*{e}^{-\frac{{E}_{A}}{R*T}}$$
(26)
$${E}_{{A}}=-{ln}\left(\frac{{k}_{1}}{A}\right)*R*T$$
(27)

Since this study treats the process in general terms and does not specify an exact catalyst, by-products are disregarded. Although water is included in this balance as a by-product, it is not relevant to an evaluation from the demand perspective in this case. Excess water could be recycled and treated for use in electrolysis to optimize the process further.

The physically optimal work of the methanation reaction is thus ascertained from the energy content of the hydrogen and carbon dioxide supplied and the activation energy supplied. Equations (24) and (25) require four moles of hydrogen to produce one mole of methane. The total energy requirement of methanation can therefore be estimated with Eq. (28), incorporating the energy required to produce four moles of hydrogen (\({E}_{{{H}}_{2}}\)) and one mole of carbon dioxide. Since the origin of the carbon dioxide is not specified, the standard enthalpy of formation is employed.

$${B}_{{Methanation}}={4 E}_{{{H}}_{2}}+{H}_{{m},{{CO}}_{2}}+{E}_{{A}}$$
(28)

Evaluating the Efficiency of Heat Transfer Processes

As “Methanation” explains, heat removal is essential to more than just increasing the efficiency of the overall process. Since efficient release of the process heat enables the highly exothermic subprocess of methanation (see Sect. 3.2), heat release should be treated as a fundamental subprocess of methanation and evaluated with the PhO. The procedure is described below for any type of heat exchanger.

An evaluation based on VDI 4663 defines a minimum surface area required for heat transfer. This physically optimal surface \({A}_{{PhO}}\) is needed to transfer the heat flow required under optimal conditions. Since heat exchangers must be designed to achieve the requisite transfer performance to counteract power-reducing fouling, the heat transfer surface is sized larger (surface \({A}_{{VS}}\)). The inaccuracy of the calculation model must be factored in along with surface enlargement related to contamination. This additionally enlarges the heat transfer surface (surface \({A}_{{S}}\)), yielding the total real heat transfer surface \({A}_{{real}}\) (Eq. (29)), factoring in contamination and uncertainties. Since it is always larger than the surface required theoretically, the real transfer surface is oversized (Verein Deutscher Ingenieure e. V., 2019) (Fig. 6).

Fig. 6
figure 6

Division of a heat exchanger’s transfer surface into the physically optimal surface required, the surface required in the event of fouling, and the surface added because of potential model deviations (based on Keichel (2017))

Full size image
$${A}_{{real}}={A}_{{PhO}}+{A}_{{vs}}+{A}_{{s}}$$
(29)

Heat exchangers can be evaluated based on VDI 4663 with Eq. (5). The heat flux in real terms \({\dot{Q}}_{{real}}\) and the heat flux under optimal physical conditions \({\dot{Q}}_{{PhO}}\) must be determined. The heat flux \({\dot{Q}}_{{real}}\) is defined by the fluid mass flow \(\dot{m}\), the average specific heat capacity \({c}_{{p},{m}}\), and the real temperature difference \({\Delta \vartheta }_{{real}}\) (Glück 2017).

$${\dot{Q}}_{{real}}=\dot{m}* {c}_{{p},{m}}* {\Delta \vartheta }_{{real}}$$
(30)

The heat flux under optimal physical conditions \({\dot{Q}}_{{PhO}}\) is defined, factoring in the operating conditions (Verein Deutscher Ingenieure e. V., 2019).

$${\dot{Q}}_{{PhO}}=\dot{m}* {c}_{{p},{m},{PhO}}* {\Delta \vartheta }_{{PhO}}$$
(31)

Assuming a constant inlet temperature, the physically optimal outlet temperatures are the highest or lowest temperatures possible, depending on the fluid analyzed. This yields maximum temperature differences specific to the process equipment, operation, and thus maximum heat flows.

The outlet temperatures are defined by the performance, the heat transfer surface \({A}_{{ges}}\), and the heat transfer coefficient under optimal physical conditions \({k}_{{PhO}}\). To this end, the heat exchanger is assumed to run under perfect operating conditions.

In counter-flow operation, the temperatures are defined by Eqs. (32) and (33) (Glück 2017).

$${\vartheta }_{1,{PhO}}^{{^{\prime}}{^{\prime}}}={\vartheta }_{1}^{{^{\prime}}}-\frac{1-{e}^{-\left(1-\frac{{\dot{C}}_{1}}{{\dot{C}}_{2}}\right)*\frac{{k}_{{PhO}}*{A}_{{ges}}}{{\dot{C}}_{1}}}}{1-\frac{{\dot{C}}_{1}}{{\dot{C}}_{2}}*{e}^{-\left(1-\frac{{\dot{C}}_{1}}{{\dot{C}}_{2}}\right)*\frac{{k}_{{Pho}}*{A}_{{ges}}}{{\dot{C}}_{1}}}}*\left({\vartheta }_{1}^{{^{\prime}}}-{\vartheta }_{2}^{{^{\prime}}}\right)$$
(32)
$${\vartheta }_{2,{PhO}}^{{^{\prime}}{^{\prime}}}={\vartheta }_{2}^{{^{\prime}}}-\frac{1-{e}^{-\left(1-\frac{{\dot{C}}_{2}}{{\dot{C}}_{1}}\right)*\frac{{k}_{{PhO}}*{A}_{{ges}}}{{\dot{C}}_{2}}}}{1-\frac{{\dot{C}}_{2}}{{\dot{C}}_{1}}*{e}^{-\left(1-\frac{{\dot{C}}_{2}}{{\dot{C}}_{1}}\right)*\frac{{k}_{{PhO}}*{A}_{{ges}}}{{\dot{C}}_{2}}}}*\left({\vartheta }_{1}^{{^{\prime}}}-{\vartheta }_{2}^{{^{\prime}}}\right)$$
(33)

The heat exchanger’s operating mode defines the thermal transmittance coefficient, which is a function of the heat transfer coefficients \({\alpha }_{{i}}\) and thermal conductivity \(\lambda\). The heat transfer coefficients characterize the intensity of heat transfer at the interfaces and are described by the Nusselt number.

Since it does not occur under optimal physical conditions, fouling is disregarded in the definition of \({k}_{{PhO}}\) (Böckh and Wetzel 2017).

$$\frac{1}{{k}_{{PhO}}}=\frac{1}{{\alpha }_{1}}+\frac{s}{\lambda }+\frac{1}{{\alpha }_{2}}$$
(34)

The physically optimal temperature difference \({\Delta \vartheta }_{{PhO}}\) can be calculated by using the input and the physically optimal output temperature or the equation for the energy balance (Eq. (31)). Equation (31) simultaneously describes the physically optimal heat flow. This makes it possible to define the PhO factor \({f}_{{PhO}}^{K}\).

The PhO factor is calculated based on \({\dot{Q}}_{{real}}\) and \({\dot{Q}}_{{PhO}}\).

$${f}_{{PhO}}^{K}=\frac{{c}_{{p},{m}}* {\Delta \vartheta }_{{real}}}{{c}_{{p},{m},{PhO}}* {\Delta \vartheta }_{{PhO}}}\le 1$$
(35)

Since losses must be allowed for, the physically optimal heat flux cannot be obtained under real terms. This makes the factor suitable for targeted optimization. Targeted process optimization is possible based on this PhO factor.

Process optimization with VDI 4663

The importance of key indicators that can be used to optimize processes is growing steadily in manufacturing. It is essential that functional and, above all, meaningful key indicators are generated (Keichel and Sankol 2016). Since it defines an ultimate reference point with the PhO, VDI 4663 is a tool well suited for targeted process optimization. The evaluation of complex overall processes necessitates analyzing several subprocesses. Methods for identifying subprocesses that ought to be optimized are examined below.

The optimization of a complex process requires knowledge of all subprocesses’ PhO. The maximum optimization capability can be determined for each subprocess by comparing the energy required under real terms with the physically optimal energy consumption. This principle can be applied to both the consumption (Eq. (36)) and the demand perspective (Eq. (37)).

$${\Delta \dot{V}}_{{max},{i}}={\dot{V}}_{{PhO}.{ i}}-{\dot{V}}_{ {i}}$$
(36)
$${\Delta \dot{B}}_{{max},{i}}={\dot{B}}_{{ i}}-{\dot{B}}_{{PhO},{ i}}$$
(37)

These values can also be determined by using PhO factors. Equation (38) is applicable to the consumption perspective, while Eq. (39) is applicable to the demand perspective.

$${\Delta \dot{V}}_{{max},{i}}=(1-{f}_{{PhO},{i}}^{V}){\dot{V}}_{{PhO},{i}}$$
(38)
$${\Delta \dot{B}}_{{max},{i}}=({f}_{{PhO},{i}}^{B}-1){\dot{B}}_{{PhO},{i}}$$
(39)

When analyzing a process’s energy consumption, the subprocess with the highest value of \({\Delta \dot{V}}_{{max}}\) and \({\Delta \dot{B}}_{{max}}\) ought to be optimized. The primary energy forms may have to be factored in in order to obtain generally valid results (Volta 2014).

Identifying the subprocess that has the greatest potential to reduce CO2 based on \({\Delta \dot{V}}_{{max}}\) and \({\Delta \dot{B}}_{{max}}\) is also conceivable. To this end, the subprocesses’ CO2 emission per watt is determined by including an according factor.

$${\Delta {m}_{{CO}}}_{2,{max},{i}}={\Delta \dot{B}}_{{max},{i}}*\frac{{kg}_{{{CO}}_{2}}}{W}$$
(40)

Other evaluation criteria can be analyzed. This method could be used, for instance, to identify the subprocess with the greatest potential for monetary savings in order to optimize it subsequently.

The indirect PhO factor based on indirect efficiency facilitates targeted optimization of subprocesses. A process’s output and losses are used to determine its input (Grote et al. 2014).

$${Input}={Output}+{Losses}$$
(41)

The indirect PhO factor is defined by inserting Eq. (41) in Eq. (2).

$${f}_{{PhO},{ind}.}^{B}=1+\sum_{{i}=1}^{n}\frac{{{Loss}}_{{i}}}{{{Output}}_{{ges}}}\ge 1$$
(42)

The specific energy loss to be optimized is the maximum ratio of dissipated power to the overall output. Again, costs or emissions can be optimized along the lines of Eq. (40).

Conclusion and outlook

This study opens by explaining the relevance of P2G technologies for the inevitable decarbonization of various industrial sectors. It then goes on to examine various P2G applications as well as the deficits of current evaluation methods. The PhO is introduced as an energy indicator that not only specifies the current state of a technology but also its maximum optimization capability. This key indicator is used to evaluate the energy efficiency of power-to-methane subprocesses, e.g., electrolysis, methanation, and heat release. The results obtained furnish the basis for evaluating the efficiency of the process steps with the aid of real measured values. Not only can existing plants be evaluated for their resulting overall efficiency but planned processes can also be compared.

Since the definition of the PhO represents an idealized reference point dictated by the laws of physics and is thus independent of the state of the art, the method can be used to evaluate processes continuously. The impossibility of surpassing the PhO technically eliminates any need to recalculate the idealized reference process ever, even if the state of the art or research changes.

Since the PhO is bound by the limits of physics and assuming that physics includes the laws of chemistry and biology, the models presented in this study are transferrable to other processes. When thermodynamics is factored in, other P2G or even P2X process steps can be evaluated along the lines of the analysis described in this paper. The electrolysis model, for instance, is transferrable to any water splitting process and facilitates study of other electrochemical processes. The thermodynamic analysis of methanation is transferrable to other chemical reactions, such as the production of methanol from hydrogen and carbon dioxide, factoring in the respective thermodynamics and stoichiometry. The division of the existing process into reasonable subprocesses is crucial to the model’s transferability to other processes. This makes it possible during the evaluation to disregard systems that control process conditions. An example of such a control system is the heat exchanger analyzed in this study.

The aggregation of the individual processes’ key indicators in one overall key indicator that defines the maximum capability to optimize an overall process will have to be studied and defined in the future. Additional effects also require study. Optimizing a subprocess might improve its efficiency while diminishing the main process’s efficiency, for instance. Findings from the current WIPANO research project greoKEMS and the research project HyPerFerment are being and will be used to verify and refine the method of the physical optimum.

Symbols used

A

[-]

Frequency factor

A

[m2]

Surface

B

[e.g., W]

Demand

C

[WK−1]

Heat capacity flow

c p

[Jkg−1 K−1]

Specific heat capacity

∆RGm

[J mol−1]

Molar reaction energy

∆RHm

[J mol−1]

Molar enthalpy of reaction

∆RSm

[J mol−1 K−1]

Molar entropy of reaction

E A

[J mol−1]

Activation energy

E j

[J mol−1]

Energy required to produce one mole of component j

F

[As mol−1]

Faraday constant

F

[-]

PhO factor

f

H

[J mol−1]

Molar standard enthalpy of formation

k

[Wm−2 K−1]

Thermal transmittance coefficient

k i

[s−1]

Rate constant of a first order reaction i

m

[kg]

Mass

p

[bar]

Operating pressure

P el

[J mol−1]

Power of the reaction per mole hydrogen or water

Q

[W]

Heat

R

[Ω cm2]

Electric resistance

R

[J mol−1 K−1]

Gas constant (R = 8314 J mol−1 K−1)

s

[m]

Length

S irr

[J mol−1 K−1]

Irreversible entropy production flow

T

[K]

Operating temperature

U

[V]

Voltage

V

[e.g., W]

Consumption

z

[-]

Valence

z a

[-]

Conversion rate of reaction

Greek symbols

α

[Wm−2 K−1]

Heat transfer coefficient

λ

[Wm−1 K−1]

Thermal conductivity

ϑ

[K]

Temperature

Subscripts and superscripts

0

Based on standard condition

Electrolysis

Value related to water electrolysis

e

Electrode

sep

Separator

ges

Total

i

Value related to subprocess i

j

Value related to component j

K

Capacity

kin

kinetic

m

Average/molar

Methanation

Value related to methanation

PhO

Physical optimum

rev

Reversible process

S

Safety

VS

Fouling

zell

Cell

Abbreviations

EFF

Efficiency

IE

International efficiency

PhO

Physical optimum

P2G

Power-to-gas

P2X

Power-to-X

UK

United Kingdom of Great Britain and Northern Ireland

UN-FCCC

United Nations Framework Convention on Climate Change