Abstract
Energy efficiency in buildings has garnered significant attention in Saudi Arabia. This paper outlines the potential effects of higher residential efficiency on electricity load profiles in the Kingdom. It further presents the associated benefits that could have been realized by the local utilities in 2011. To perform the analysis, we designed an integrated methodology in which an engineering-based residential electricity demand model is used within an economic equilibrium framework. The modeling approach allows us to capture the physical interactions arising from higher efficiency and the structural changes that could occur in the economy beyond the end-consumers. Raising the average air-conditioner energy efficiency ratio (EER) to 11 British thermal unit (BTU)/(Wh) from its 2011 average would have saved 225,000 barrels/day of crude oil in electricity generation. Alternatively, increasing the share of insulated homes from 27 to 64 % would have allowed the power sector to lower its use of the fuel by 158,000 barrels/day. Combining both measures in a single simulation yields incremental yet not additive reductions. All alternative scenarios reduce costs to the utilities and improve the average thermal efficiency for the electricity generated. The studied efficiency options shift the load curve downward during the peak load segment when the least efficient turbines would be used. We additionally show how efficiency improvements in end-uses can affect the decisions of other sectors in the economy.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
In light of rapidly increasing domestic demand for fossil fuels, Saudi Arabia has been exploring various options to lower its energy consumption. Matar et al. (2015) have previously shown potential energy savings by altering the local fuel prices offered to industrial firms and incentivizing the utilities to adopt more efficient technologies. Their study did not consider any deviations in energy use by the end-consumers. Further gains could be realized by targeting the residential sector as it is responsible for half of local electricity demand.
The government has placed emphasis on efficiency as an alternative to price reform for households, as has been shown with the efforts of the Saudi Energy Efficiency Center and the Ministry of Water and Electricity. Public awareness campaigns have complemented the recent introduction of more stringent standards for air conditioners and the requirement for new residences to have thermal insulation. This study investigates the system effects of the widespread adoption of these efficiency measures.
The Kingdom’s pursuit of higher residential efficiency is largely motivated by the rapid growth in electricity use and the associated reliance on oil for power generation. With crude oil sold to utilities at US$4.24/barrel, the substantial use of the fuel domestically generates a large opportunity cost to the government. Of course, other benefits like lower pollutant emissions could be also achieved.
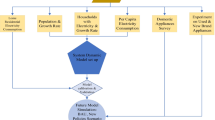
The objectives of this analysis are twofold: one is to calculate the potential shifts in the hourly system-level power demand resulting from more efficient households. The other is to quantify the impact of the new load curves on the operations of the electricity sector. To accomplish this, we simulate the effects that efficiency measures have on residential electricity demand using an engineering-based approach. The simulations are then linked with the recently developed KAPSARC Energy Model (KEM) for Saudi Arabia. KEM is a partial economic equilibrium model that represents six of the country’s energy intensive sectors. Matar et al. (2014, 2015) describe KEM and its calibration to the year 2011.
Any changes the electricity sector makes to its operating decisions may have a cascading impact on other sectors in the economy. For instance, reduced use of refined oil products for power generation would cause an operational change in the refining sector, which would also have an effect on the grade and quantity of crude oil supplied to the domestic refineries. Any quantities of crude oil saved, whether in the power plants or refineries, could be exported immediately or stored for future generations.
We could not find many studies on the impact of more efficient electricity use by households on the rest of the economy. Recently, Lecca et al. (2014) investigated the greater effects of a general household efficiency improvement using a methodology based on the input-output approach. This methodology represents the flows of goods and services between production sectors using technical coefficients. We show in this paper that other sectors in an economy can also experience structural changes as a result of more efficient households. Economic models founded on the input-output technique use constant annual technical coefficients and hence may not capture these factors. Although we represent the intraday variations in electricity demand and generation, it is important to note that Lecca et al. (2014) take a general equilibrium approach whereas our work takes a partial equilibrium view.
While there have been several studies on modeling end-use energy consumption in Saudi Arabia, they have used top-down approaches and none have focused on the residential sector per se. For example, Ibrahim (2011) and Gately et al. (2012) applied econometric methods to study the relationship between energy consumption and socio-economic factors, like price and income. In this respect, we demonstrate in this paper the insights gained by simulating hourly electricity use using engineering relationships. Furthermore, this paper fills the void in the literature pertaining to Saudi Arabia.
To our knowledge, an end-use model of the type presented here has never been integrated with an economic model. Kannan and Strachan (2009) applied the UK MARKAL model to study the system-wide effects of decarbonization and the associated role of the residential sector in the UK. Their model contained a disaggregated representation of end-uses by the residential sector, but it did not capture the energy use detail of building stock simulation models. There have, however, been several household electricity demand studies conducted for other regions using the engineering approach applied in this work (e.g., MacGregor et al. 1993; Wan and Yik 2004; Shimoda et al. 2004).
The paper is structured as follows: The next two sections provide an overview of electricity demand, the make-up of residences in Saudi Arabia, and the role of local energy prices. The modeling approach and the integration with KEM are then detailed, followed by a discussion of the data used for calibrating the residential model. The paper is concluded with the presentation and discussion of the results.
A background of Saudi electricity demand and the residential sector
Electricity demand in Saudi Arabia is characterized by the average hourly loads shown in Fig. 1. The four regions correspond to the operating areas of the Saudi Electricity Company (SEC), which is the largest local electricity producer and the sole grid operator. The loads reflect the seasonal effects on electricity demand, driven by the use of air conditioning in the warmer months. The great amount of electricity flowing to residential air-conditioning units has been repeatedly brought up in the past. Faruqui et al. (2011) have stated that cooling demand is responsible for 70 % of the sector’s electricity consumption.
2011 average regional load curves for weekdays (source: Electricity and Cogeneration Regulatory Authority 2011)
According to the latest figures from Enerdata (2015), the average household in Saudi Arabia consumed 23 MWh of electricity in 2013, which was the third highest globally after Kuwait and Qatar. For comparison, households in the USA and China consumed 12.2 and 1.5 MWh that year, respectively. With this in mind, the residential sector has historically represented around half of domestic electricity consumption. Figure 2 illustrates the geographical representation in our model and the regional shares of household electricity consumption for the year of our analysis. Lesser to some extent in the eastern region due to the large presence of industry, the residential sector is a key driver for national electricity demand.
Shares of electricity consumption by sector and region in 2011 (source: Saudi Arabian Monetary Agency (2014))
Furthermore, the Saudi Central Department of Statistics and Information (CDSI) decomposes the regional housing stock into traditional houses, villas, apartments, floors in villas or traditional houses, and other residences. Other residences include huts and tents, which are not typically connected to the power grid. Figure 3 shows the composition of the stock in past census years. The share of traditional houses and “other” residences in the stock has gradually decreased over the 18-year period. The share of apartments has conversely experienced consistent growth, comprising more than 40 % of the housing stock in 2010.
The role of energy prices for utilities and households in Saudi Arabia
The local power sector is dominated by SEC, owned mostly by the government and some independent power producers. Power plants face regulated prices for the fuels they purchase and their electricity output. For example, crude oil and natural gas are sold to the utilities at US$4.24/barrel and US$0.75/MMBTU, respectively. These prices have had adverse effects on the firms’ investment decisions. Lower-capital cost and inefficient plants have been favored to more expensive and efficient technologies. As described in the following section, although the power sector is part of an integrated model of the energy economy, it makes decisions based on the costs it faces, which include these administered fuel prices.
Moreover, residential customers pay 1.3 US cents/kWh for the first 2 MWh consumed/month, and the tariff progressively increases for incremental levels of consumption. The fixed tariff structure, which is applied nationally, means any changes in demand resulting from higher household efficiency may affect the average and marginal costs of delivering electricity, but that will not translate to a change in price for households.
The low electricity price does not generally encourage higher energy efficiency. Local government agencies have so far taken the route of driving efficiency through enforcement of higher standards rather than inducing adoption by increasing the electricity price. The Saudi Standards, Metrology and Quality Organization (2013) recently raised the minimum EER (rated at 35 °C) of new air conditioners to 9.5 British thermal unit (BTU)/(Wh) from 7.5 BTU/(Wh); this standard is expected to further rise to 11.5 BTU/(Wh) in the near term. The already-established Saudi Building Code also addresses standards for material properties of residential units, but due to lack of compliance, the government mandated in 2013 that all new residences must have thermally insulating materials to be connected to the grid.
Methodology and interfacing the model with KEM
An engineering-based model was adopted to capture the physical and technological factors that impact electricity use in residences. This approach is capable of addressing policy and technology issues beyond the scope of econometric and activity-based methods. The operational decisions of the power sector change throughout the day depending on the level of expected demand. The daily demand profile can be highly influenced by how much cooling and heating households require in order to maintain comfort. Furthermore, the level of electricity used to maintain comfortable indoor conditions is contingent upon structural attributes of homes, occupancy and equipment characteristics, and outdoor weather variation. These temporal interactions between physical properties, demand, and electricity generation affect the fuel use and equipment ramping decisions made by electricity producers. The model’s hourly resolution also allows the simulation of the intraday effects of any load-altering efficiency measure.
Due to the significance of heating, ventilating, and air conditioning (HVAC) on the demand for electricity in Saudi Arabia, the residential model constructs power load curves using the electricity consumption of HVAC systems as the foundation upon which other end-uses are added. The model simulates the conductive, convective, and radiative heat gains that take place in residential enclosures by taking into account outdoor conditions and residence characteristics. The required operating level of the HVAC system to achieve some desired indoor air conditions is also calculated.
An in-depth description of the modeling methodology and validation is given in Appendix 1. The simulations are performed for archetypes that represent the housing stock for three seasonal periods and all regions. The results are scaled up in accordance with the number of each residence type in the regional housing stock.
KEM is designed to handle the regulated prices that permeate the Saudi energy economy. Rather than restricting the model to a system optimization approach, to find an equilibrium, each sector in KEM optimizes its own cost or profit based on the costs and prices it sees. The power sector is represented as a cost minimizer that is now structured to use chronological load curves for each region to make equipment and fuel use decisions; the load curves are discretized into eight daily load segments. Considered power generation technologies include conventional thermal plants, nuclear, photovoltaic, concentrating solar power, and wind. The model structure uses variables for existing capacities, building additional plants, and the operation of the installed capacity in each load segment. A transmission network is also modeled to allow for inter-regional electricity flows. In addition to capacity balance, operation, and cost-accounting equations, reserve margin requirements may also be enforced.
The residential model was designed from the outset to be linked with KEM. As such, the seasonal and regional disaggregation is consistent between the two models. Almost 200 hourly load curves are generated for the combination of archetypes, types of day, seasons, and regions. Thus to reduce computation time, the model sequentially solves through all seasons and regions while running a separate yet concurrent process for each archetype; the power loads for the weekdays and weekends/holidays are computed simultaneously. The results are output to a spreadsheet, which is then read by KEM for further pre-processing to convert from hours to the discretized load segments. KEM stores the baseline residential load data, and the updated loads are picked up as alternative residential demand scenarios are run. The two data sets are needed to calculate the resulting deviation from the 2011 system load curves.
Parameterization of the residential model for Saudi Arabia
The model is calibrated such that regional electricity consumption matches the 2011 data published by the Electricity and Cogeneration Regulatory Authority (2011). The calibration relies on the data gathered through the meter reading and billing process carried out by SEC. The calibrated electricity use of consumer electronics, home appliances, lighting, and water heaters is also matched with the figures provided by Faruqui et al. (2011). Appendix 2 details the assumptions and parameters used for calibration.
Description of scenarios
The residential model is jointly run with KEM in a counterfactual framework looking back on the year 2011. While the household demand varies by scenario, the power sector is only allowed to use its existing capacity for that year to meet total demand. In addition to a baseline case replicating the consumption in 2011 called the Reference scenario, three alternative scenarios have been designed to observe the effects of more efficient residences on the system load and the operating decisions of the electricity sector. These hypothetical scenarios are inspired by the recent regulations to enforce more efficient air-conditioning performance and increase the prevalence of thermal insulation. The two measures have garnered the greatest interest domestically and target electricity demand during peak hours. The analysis considers that households maintain the same level of service from their equipment; for example, the thermostat set-point does not change across scenarios.
The scenario higher prevalence of thermal insulation explores what would have been the impact on the power system had there been more insulated residences in 2011. The scenario stipulates that 90 % of villas, apartments, and single-floor residences in villas have polystyrene insulation material; this would raise the percentage of insulated residences in the entire housing stock to nearly 64 % compared with the baseline value of 27 %. The model converts the non-insulated archetypes to adopt the material characteristics of those with polystyrene insulation as described in Table 6 in Appendix 2.
Moreover, the implementation of more stringent EER standards for new air-conditioning units could substantially reduce the electricity use in the baseline case. The scenario increased EER studies the system effects of improved air-conditioning performance in the Saudi residential sector. Inspired by the gradual implementation of higher standards, we carried out the simulation of the scenario for a range of EER values. The simulations are performed over values ranging from the 2011 local average of 7 to 11 BTU/(Wh), which according to AMAD for Technical Consultation and Laboratories (2011) would bring it closer to the market averages in the USA, China, and South Korea.
The third alternative scenario investigates the effects of combining the features of the first two cases by increasing the national EER to 11 BTU/(Wh) and imposing the 64 % share for insulated residences. This scenario is called combined EER and insulation.
Results and discussion
Table 1 compares the regional model results in the reference scenario to the actual residential electricity consumption in 2011. Current grid infrastructure does not track power flows to their end-use destination for determining sectoral load curves. It is still useful, however, to compare the simulated residential curves with the measured loads in the whole system. Figures 4, 5, and 6 show the residential profiles in the reference case and the measured system-level loads for each seasonal period. The system loads include the consumption by the industrial, commercial, and government sectors. The measured loads on weekends/holidays exhibit a similar profile to those on weekdays, although they are slightly lower. The similarity of the profiles’ shapes is a feature of cooling demand that may not highly depend on type of day. The curves for residences are constructed using the sum of the model’s regional outputs. The slight differences in the residential loads between weekdays and weekends/holidays are due to differing occupancy patterns.
The simulated and measured load profiles exhibit visible correlation during the early evening period when lights would typically be turned on and throughout the day as cooling demand gradually increases before declining in the evening. While there is overall correlation, slight deviations in some seasons in the morning period may result from the approximated solar relationships for Saudi Arabia and the relatively coarse hourly discretization.
The load-shifting potential of the efficiency measures
Figures 7, 8, and 9 illustrate how the seasonal load curves for the entire power system would change in the alternative scenarios. As to be expected, the least impact on load is observed in the winter, and the greatest reductions take place in the warmer months. There is a time lag when heat conducts through the walls and roof of residential enclosures. The reduction of heat gain, and ultimately the cooling load, does not happen instantaneously, as shown by the load curves for higher prevalence of thermal insulation. The load reductions for the increased EER scenario can be realized immediately as this case involves a direct use of electricity as opposed to an indirect effect. Some regions may not require air conditioning depending on time of day or seasonal period. The regional components of these load demands are what KEM reads for finding the equilibrium.
The implications of more efficient households on the power system
For each scenario, Table 2 shows the electricity consumption by residences, the average thermal efficiency for total electricity generated, and the reductions in total cost and crude oil consumption for the power sector.
An increase of the average EER to 11 BTU/(Wh) and the higher prevalence of thermal insulation scenario would have resulted in a 22.8 and 16.1 % decrease in residential electricity consumption, respectively. Combining both efficiency options in a single simulation would have resulted in incremental yet not additive reductions in electricity use. The two measures have interacting features. Reducing the heat gain would lower the extent to which air conditioning is utilized, thus lessening the impact of a higher EER. The non-additive property of combining efficiency measures is less obvious for the seasonal reduction in oil use. This is because the power sector can substitute the use of some fuels between seasons as a result of altered regional load curves.
The reductions in cost take into account fuels purchased at the locally administered prices, non-fuel variable operations and maintenance (O&M) costs, and fixed O&M costs. Total and average cost reductions in the alternative scenarios arise from the lowered operation level to meet demand and the more efficient utilization of the installed power capacity.
The average thermal efficiency for the total electricity generated increases from 34 % in the reference scenario to 35 and 35.5 % in the higher prevalence of thermal insulation and increased EER scenarios, respectively. Combining the features of those two scenarios yields an average thermal efficiency of 36.3 %. The residential measures analyzed target the peak load hours, when the least-efficient and highest-marginal-cost equipment would be operated. While this equipment is not retired in the model, the utility does not operate them. Figure 10 illustrates this behavior, showing the model results for national dispatch by technology during a summer weekday; there are very small photovoltaic capacities that always produce power during the day. Combined-cycle and steam turbine plants are used to satisfy the base load.
Figure 11 shows the corresponding fuel consumption in the model’s load segments on a summer weekday. Any reduction in local electricity demand causes a decline in the amount of crude oil used by the power sector. Natural gas is highly demanded domestically because of its administered fuel price relative to the price of crude oil and the thermal efficiencies of existing plants that use gas. Gas supply, however, is constrained below the level of fuel demand and crude oil is hence used as the marginal fuel for generation. The use of oil in power plants rises sharply in the summer months and exhibits a periodic consumption pattern throughout the year. Since the greatest reductions in electricity demand and associated oil consumption are observed in the summer months, these measures help the power sector mitigate the annual peaks in consumption that cut into Saudi Arabia’s ability to export oil.
Furthermore, Fig. 12 presents the residential electricity use and the change in oil consumption by the power sector as the EER is gradually raised to 11 BTU/(Wh).
Primary and secondary effects contributing to lower fuel use for power generation
The results highlight the presence of two effects that influence the amount of fuels burned by the power sector. Firstly, there is a direct reduction in fuel use caused by lower electricity production. Secondly, the more efficient utilization of the generation capacity leads to less fuel consumed per unit of electricity produced. Table 3 shows the national reductions of oil use in power plants attributed to both of these effects.
The fuel savings due to lower production are calculated as the change in electricity output using oil multiplied by the average heat rate of oil-generated electricity in the reference scenario. Similarly, the savings due to higher efficiency are computed as the change in the average heat rate of oil-generated electricity multiplied by the quantity of electricity produced using oil in the alternative scenarios. In the combined EER and insulation scenario, for example, the average fuel use rate of oil-burning plants decreases from about 1900 to 1723 barrels/GWh. This is directly due to lower dispatch using open-cycle gas turbines.
It can be seen that neglecting the secondary factor may result in underestimating the magnitude of the economic domino effect caused by more efficient households. In the context of this analysis, higher energy efficiency for end-uses can cause other sectors in the economy to also become more efficient. For instance, the shift in electricity demand during the peak load segments as a result of combining higher EER and insulation would yield a lower and flatter load profile. This means the power sector would not have to operate low-capital-cost yet high-operation-cost turbines typically reserved for only a small number of hours in the year. Models using the input-output approach would not be able to capture these secondary sectoral interactions. In those models, the coefficients relating the fuel-supplying sectors and the power sector remain constant.
Conclusion
This analysis demonstrated the potential domino effect of improving energy efficiency in the Saudi residential sector. It particularly highlighted the benefits that could have been realized by the local power sector in 2011 as it reacts to changes in the hourly electricity demand. An engineering-based residential electricity model was used to assess the load-shifting potential of increased thermal insulation adoption and higher air-conditioning efficiency. The load curves are linked to a bottom-up economic equilibrium model to simulate the interactions with the utilities. Our approach captures the physical relationships that dictate the magnitude and time of load-shifting as a result of higher efficiency.
All alternative scenarios resulted in significant reductions in oil consumption for power generation and lower costs to the power sector. While two cases tested the individual effects of higher EER and increased levels of insulation on electricity use, a third showed there would be additional yet not necessarily additive benefits of applying them together. The reason for this is that both measures have interacting physical features. The model could also be used to test other measures or vary the parameters of the presented scenarios. For example, the use of different materials for thermal insulation or the application of low-solar-absorptivity paints for external walls may be investigated.
Furthermore, the results show more efficient use of the existing power generation capacity due to the widespread adoption of the two efficiency measures. The least efficient gas turbines, which are put off to only be used during the highest load periods, are forgone as the measures lower power demand during peak hours. The fuel-saving benefits for the power sector when peaking equipment would be ramped up are greater than those realized if the electricity reduction takes place in the base load segment. Also, consumption of crude oil for power generation exhibits large swings throughout the year. The efficiency options analyzed lower the electricity use for space cooling, and would therefore mitigate the large seasonal swings in demand.
We also demonstrate the capabilities of applying engineering end-use models within a bottom-up economic framework. Such linkage could allow the study of policy issues not achievable through other methods. The approach we take captures the physical factors that govern hourly demand for electricity, which influences the decisions made by the utilities. Applications of our model cover efficiency and also extend to other topics like the deployment of distributed generation in homes, the associated impact on simulated loads, and the greater system effects. We are also working on price response features to study how households may change equipment settings or shift appliance use under various electricity pricing schemes. Such issues require factoring in physical effects shaping the load profile. Data development will also be a focus of research, as more up-to-date data is required for future work.
Notes
This is the value used by commercial software package DesignBuilder.
For most appliances, typical power ratings are taken from Gottwalt et al. (2011).
References
Al-Harigi, F., Al-Shiha, A., and Slaghor, J., 2004. Estimation of the number, size, and type of residences in the Kingdom of Saudi Arabia for the next twenty years. King Abdulaziz City for Science and Technology, pp. 119. (Arabic release)
Al-Sanea, S., Zedan, M. F., & Al-Ajlan, S. (2005). Effect of electricity tariff on the optimum insulation-thickness in building walls as determined by a dynamic heat-transfer model. Applied Energy, 82, pp. 313–pp. 330.
Al-Shaikh, S., 2003. Consumer durables industry doing well in Kingdom. Arab News. Accessed September 16th, 2014. Available at: http://www.arabnews.com/node/234969.
AMAD for Technical Consultation and Laboratories, 2011. High EER at 46 °C Kingdom of Saudi Arabia Air Conditioner Project. Presentation slides.
Bejan, A. (1993). Heat transfer (p. pp. 536,624). New York, New York: John Wiley & Sons, Inc..
Dubai Press Club, 2012. Arab Media Outlook: 2011–2015. 4th edition, pp. 155–161.
Electricity & Cogeneration Regulatory Authority (2011). Annual statistics booklet for electricity and seawater desalination industries.
Enerdata, 2015. Average electricity consumption per electrified household. Last accessed June 7th, 2015. Available at: http://www.wec-indicators.enerdata.eu/household-electricity-use.html.
Faruqui, A., Hledik, R., Wikler, G., Ghosh, D., Prijyanonda, J., and Dayal, N., 2011. Bringing demand-side management to the Kingdom of Saudi Arabia: final report. The Brattle Group, pp. 40.
Gately, D., Al-Yousef, N., & Al-Sheikh, H. (2012). The rapid growth of domestic oil consumption in Saudi Arabia and the opportunity cost of oil exports forgone. Energy Policy, 47, 57–68.
Gottwalt, S., Ketter, W., Block, C., Collins, J., & Weinhardt, C. (2011). Demand side management – a simulation of household behavior under variable prices. Energy Policy, 39, 8163–8174.
Henninger, R., & Witte, M. (2013). EnergyPlus testing with building thermal envelope and fabric load tests from ANSI/ASHRAE standard 140-2011 (pp. 3–13). United States: Department of Energy.
Ibrahim, M. (2011). Energy consumption, income and price interactions in Saudi Arabian economy: a vector autoregression analysis. Advances in Management and Applied Economics, 1(2), pp. 1–pp.21.
Jayamaha, S., Wijeysundera, N., & Chou, S. (1996). Measurement of the heat transfer coefficient for walls. Building and Environment, 31(5), pp. 399–pp. 407.
Jefferis, A., and Jefferis, J., 2013. Residential design, drafting, and detailing. Second edition. Delmar Cengage Learning, pp. 360.
Kannan, R., & Strachan, N. (2009). Modelling the UK residential energy sector under long-term decarbonisation scenarios: comparison between energy systems and sectoral modelling approaches. Applied Energy, 86, pp. 416–pp. 428.
Lecca, P., McGregor, P. G., Swales, J. K., & Turner, K. (2014). The added value from a general equilibrium analysis of increased efficiency in household energy use. Ecological Economics, 100, pp. 51–pp. 62.
MacGregor, W. A., Hamdullahpur, F., & Ugursal, V. I. (1993). Space heating using small-scale fluidized beds: a technoeconomic evaluation. International Journal of Energy Research, 17(6), pp. 445–pp. 466.
Matar, W., Murphy, F., Pierru A., & Rioux, B., (2014). Modeling the Saudi Energy Economy and Its Administered Components: the KAPSARC Energy Model. USAEE Working Paper No. 13--150. Available at SSRN: http://ssrn.com/abstract=2343342.
Matar, W., Murphy, F., Pierru A., & Rioux, B., (2015). Lowering Saudi Arabia’s fuel consumption and energy system costs without increasing end consumer prices. Energy Economics 49, pp. 558--569.
McClellan, T., & Pedersen, C. (1997). Investigation of outside heat balance models for use in a heat balance cooling load calculation procedure. ASHRAE Transactions, 103(2), pp. 469–pp. 484.
McQuiston, F., Parker, J., & Spitler, J. (2005)). Heating, ventilating, and air conditioning: analysis and design. . Sixth edition (pp. pp. 183–pp. 200). John Wiley & Sons, Inc..
Moran, M., & Shapiro, H. (2004). Fundamentals of Engineering Thermodynamics. 5th edition (p. pp. 760). John Wiley & Sons, Inc..
Neymark, J., and Judkoff, R. (2004). International energy agency building energy simulation test diagnostic method for heating, ventilating, and air-conditioning equipment models (HVAC BESTEST): volume 2: cases E300-E545. NREL/TP-550-36754.
NREL & KACST. (2014). Renewable Resource Data Center. NASA remote sensing validation data: Saudi Arabia. Accessed January 11th, 2014. <http://rredc.nrel.gov/solar/new_data/Saudi_Arabia/>.
Rehman, S., Halawani, T. O., & Husain, T. (1994). Weibull parameters for wind speed distribution in Saudi Arabia. Solar Energy, 53(6), pp. 473–pp. 479.
Saudi Arabian Monetary Agency, 2014. SAMA: annual statistics. Available at: http://www.sama.gov.sa/en-US/EconomicReports/Pages/YearStatistics.aspx.
Saudi Aramco, 2011. Kingdom energy efficiency. Saudi Aramco, pp. 6–8.
Saudi Standards, Metrology and Quality Organization, 2013. Saudi Energy Efficiency Program: Working session on the implementation of the modified Saudi standard SASO 2663/2012. Accessed August 24th, 2015. <http://www.saso.gov.sa/ar/about/partners/Documents/AC%20workshop%20v14%20-%20English.pptx>.
Shimoda, Y., Fujii, T., Morikawa, T., & Mizuno, M. (2004). Residential end-use energy simulation at city scale. Building and Environment, 39, pp. 959–pp. 967.
Wan, K. S. Y., & Yik, F. H. W. (2004). Representative building design and internal load patterns for modelling energy use in residential buildings in Hong Kong. Applied Energy, 77, pp. 69–pp. 85.
Acknowledgments
The author thanks Anwar Gasim for the estimation of lighting technology breakdown in residences. Helpful comments were provided on previous versions of the paper by Carlos A. Bollino, Frederic Murphy, Patrick Bean, David Hobbs, and four anonymous referees.
Conflict of interest
The author declares that he has no conflict of interest.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
ESM 1
(PDF 80.7 kb)
Appendices
Appendix 1: Model description
Modeling approach
We begin by establishing a simplified thermal envelope of a residence to ultimately construct a power load curve with the HVAC power use as the foundation. The outdoor conditions of interest are the hourly dry-bulb temperature (T out), the hourly total solar irradiation (I tot), and the hourly relative humidity (RHout). As detailed in the following sections, a system of equations is set up to represent the flows of mass and energy through the opaque walls and roof, windows, between the surfaces inside the conditioned zone, and the air-conditioning system. For floors that are in direct contact with a thick material layer, their contribution to the heat gain is neglected. The resulting non-linear system of equations is solved using PATHNLP as the solver and GAMS as the user interface.
The conduction of heat through composite walls and roof
The conduction heat transfer through the multi-material walls and roof of the envelope is calculated using a one-dimensional diffusion equation, fully described by Fig. 13 and Eqs. (1) to (6). Each material m corresponds to its own domain, represented by x m .L 1 to L M are the material thicknesses. T m (x m ,t) is the temperature profile along material m for time t
Where 0 ≤ x m ≤ L m in meters, 0 ≤ t ≤ 24 in hours, and α therm m is the thermal diffusivity of material m in square meters per unit of time.
Boundary conditions:
The boundary conditions on the external and internal surfaces of a wall or roof are specified as follows:
k m is the thermal conductivity of material m. To balance energy flows on the external surface, Eq. (2) shows heat conduction must equal the sum of the convective and radiative modes of heat transfer for the control volume. Moreover, the radiation component is broken up into the contribution of solar irradiation and the surface radiation induced by the temperature difference with the surroundings. Similarly on the interior surfaces, (Eq. 3) ensures the conducted heat is balanced with the convection taking place between the wall and the zone air, the radiative components of the internal heat gains (q" IHG), and the radiation absorbed by the walls from the solar energy transmitted through windows q SHG, windows.
The outdoor convective heat transfer coefficient (h conv, out) is determined using the correlation estimated by Jayamaha et al. (1996) for a low-rise surface. Values for the indoor convective heat transfer coefficient (h conv, in, surface) are reported by McQuiston et al. (2005) for the ceiling and walls. є 1 is the emissivity of material 1, σ is the Stefan-Boltzmann constant, and β is the surface tilt angle measured from the normal of the horizontal plane. F s-sky and Fs-g are the view factors from the surface to the sky and the surface to the ground, respectively. \( \left[{T}_{\mathrm{outdoor}}(t)-6 \cos \left(\frac{\beta }{2}\right)\right] \) is the effective sky temperature for a surface of any orientation as reported by McClellan and Pedersen (1997). As a common simplification, the radiative heat inside the zone is evenly absorbed by all interior surfaces.
At the interfaces between the material layers, the heat flux and the temperature are set equal across the boundaries. It is currently estimated that the materials are ideally interfaced.
Initial condition:
The periodic nature of the problem is satisfied by calibrating the data and the solution such that the 24th hour of a given day is equal to the initial condition of the following day. Due to the difficulty of obtaining an analytical solution for Eqs. (1) through (6), they are solved numerically using an implicit backwards-in-time central-in-space finite difference scheme.
Solar irradiation
Solar irradiation affects the temperature of the external surface and therefore the amount of heat transferred through the walls and roof. It is also transmitted through windows into the conditioned space. Starting with data for direct normal irradiation (I DNI ) and local time, we solve a set of trigonometric relationships that are applicable to surfaces of any orientation and geographic location (see McQuiston et al. (2005) for details). The total solar irradiation on a surface of any tilt angle is given by Eq. (7), where θ is the angle of incidence, C is an empirical ratio of diffuse irradiation to I DNI, and ρ g is the gro’und reflectance.
Infiltration heat gains
The air-change method is applied to calculate the amount of heat exchange taking place due to infiltration. For known dimensions of a conditioned space, the mass flow rate of infiltrating air (m inf) is the product of the number of air changes per hour, the zone volume, and the outdoor air density. The sensible (Qinf, s) and latent (Qinf, l) components of infiltration heat gains are entirely convective, and are defined by Eqs. (8) and (9).
ω indoor and ω outdoor are the humidity ratios for the indoor and outdoor air, respectively. m inf is the mass flow rate of the infiltrating air, Cp, air is the specific heat for air, and h fg is the latent heat of vaporization at indoor conditions.
Internal heat gains and the direct use of electricity to operate equipment
All internal heat gains are separated into radiative and convective components. Equation (10) shows the contribution of the radiative portion to the energy balance of the interior surface j. q n is the heat gain for the n-th internal heat gain element at any given hour, F rad, n is the fraction of heat gain that is radiative for element n, and Aj is the area of j. The interior surface area of a wall or the ceiling is smaller than that of the associated external surface.
We consider the effects of both sensible and latent heat by occupants. The hourly occupancy level is exogenously fixed in the model and could be the result of household surveys. Also, multiple light bulb technologies may be considered in this model structure, each with its own power rating values and exogenously specified utilization schedule. The schedules of occupancy and equipment use may be imposed differently for weekdays and weekends/holidays.
Heat transfer through windows
The two modes of heat transfer considered for windows are solar radiation transmission and conduction. Solar radiation is mostly transmitted to the internal zone, and is decomposed into direct and diffuse solar heat gains, q TSHG, direct and q TSHG, diffuse. The transmission level of radiation varies by window type, which would be manually defined in the model structure. The transmittance of direct radiation also varies throughout the day as the sun moves across the sky. As shown by Eq. (11), direct solar heat gains are partially reflected by the floor, and the total solar heat gain, defined by qSHG, windows, is estimated to distribute evenly on the internal surfaces. (1–a floor, sol) denotes the fraction of heat reflected. A shading factor is also included to allow variation in the level of internal shading.
The conduction heat gain through windows is estimated by Eq. (12), where the convective component (Qwindows, conv) is calculated. F concv is the convective fraction of the heat gain and U windows is the windows’ overall heat transfer coefficient.
System load
Taking the previous heat gains into account, the system load is represented in two ways:
By convention, the system load is negative when cooling and positive when heating. h return is the enthalpy of the return air and h supply air is the enthalpy of the air supplied to the zone by the air handling unit (AHU). m return air and m supply air are the mass flow rates of the return and supplied air, respectively.
The air handling unit and total electric power consumption
Illustrated by the flows in Fig. 14, we solve a set of mass and energy balance relationships for the air flowing through the AHU. Assuming steady state and steady flow, the model allows air to be recirculated, released to the atmosphere, and/or drawn in from outside. The electricity requirements for the fans are calculated by applying energy balances using the return and supply fans, the cooling and heating coils, and the mixing box as the control volumes. A specific fan power (SFP) parameter, which may be defined as the pressure rise across a fan divided by its efficiency, is also specified for the fans.
The individual power consumption components are summed as shown by Eq. (15) to obtain the total electricity power load, W total. W supply fan, and W return fan are the power input by the supply and return fans, respectively. The direct uses of electricity by appliances and lighting are denoted by W equipment and W lighting, respectively. COP is the coefficient of performance of the refrigeration cycle transferring heat through the coil.
Testing the model
In this section, we focus on testing the physical representations of the heat transfer and air flows in the AHU.
The representation of the AHU
As a first step of verification, the code representing the energy and mass balances within the AHU is benchmarked against the results of TRNSYS-TUD, DOE-2.2, and HOT3000 for the scenario named case E300 by Neymark and Judkoff (2004). This scenario uses New Orleans, Louisiana, as the geographical reference. The details of the scenario, including envelope characteristics, information on outdoor air properties, fan performance, refrigeration cycle performance, and internal heat gain schedule are described by Neymark and Judkoff (2004). This test case is implemented to test the portion of the code dealing with the AHU. Fig. 15 shows the coil load profiles calculated by each model. The mean absolute percentage error relative to the average result of the other three models is found to be 3.29 %.
The conduction and system load equations
As an additional step of verification, we also run the scenario called case 195 as presented by ANSI/ASHRAE Standard 140-2011 and Henninger and Witte (2013). This case is especially suitable for our model as it enforces a constant zone temperature throughout the day. Using Golden, Colorado, as the studied location, case 195 tests the section of the code dealing with conduction through opaque surfaces and the system load. Table 4 presents the physical characteristics of the building envelope. The envelope’s dimensions are 8 × 6 × 2.7 m.
Moreover, Table 5 shows other specified parameters for the scenario run. The convective heat transfer coefficient for the ceiling differs for cooling and heating conditions. In the hot summer months, the temperature of the indoor air is lower than that of the internal surface, and thus the direction of heat flow is downward. In contrast, the direction of the heat flow is upward during a cold day. There is no infiltration component, internal heat gains, or windows. The hourly weather data were provided with ANSI/ASHRAE Standard 140-2011 in a typical meteorological year (TMY) file
ASHRAE Standard 140 shows that the maximum cooling and heating loads for case 195 took place on July 26th and January 4th, respectively. Running our model yields a maximum cooling load of 0.751 kW, compared with 0.729 kW using EnergyPlus and 0.651 kW for ANSI/ASHRAE Standard 140-2011. The value is in line with the EnergyPlus result; however, it exceeds the standard established by a significant percentage. Furthermore, the peak heating load in the winter is determined by the model to be 1.956 kW, compared with 2.090 kW found with EnergyPlus and the 2.004 kW established by the ASHRAE standard
Appendix 2: Parameterization of the residential model
Residence types and their characteristics
The regional composition of the housing stock is obtained from the results of the 2010 census carried out by the CDSI. Eight archetypes are incorporated to represent the housing stock in Saudi Arabia as described by Fig. 16, Table 6, and the following calibration sections. The materials in Table 1 are listed from the exterior surface to the interior surface. Based on the results of the latest census, traditional houses are assumed to be constructed using mud bricks, while villas and apartments are constructed using concrete.
Saudi Aramco (2011) additionally indicated that 27 % of residential units in Saudi Arabia have insulation materials. We estimate that traditional residences do not have such material installed due to their vintage. Polystyrene is here used as the insulation material, since it is commonly used with concrete structures (Al-Sanea et al. 2005).
Thermophysical properties of enclosure materials
The thermal conductivity (k), thermal diffusivity (a them), solar absorptivity (a sol), and solar emissivity (є) are documented by Bejan (1993) and McQuiston et al. (2005) for the materials used in the archetypes; the input values are shown in Table 7. Values for solar absorptivity and emissivity are only given for external surfaces.
Occupancy
Household size, shown by Table 8, is determined from the 2010 census for each region and residence type. The hourly occupancy levels are assumed as illustrated in Fig. 17 in fraction of household size. The amounts of heat gain contributed by people and other internal heat gain elements are published by McQuiston et al. (2005).
Archetype dimensions
The dimensions of the thermal envelopes are calculated based on household size and the values of residential surface area per inhabitant reported by Al-Harigi et al. (2004). Since the household size varies by region and residence type per the Saudi census, this means the dimensions will also vary by region and residence type. Once the total surface area of the dwelling is calculated, estimates of average number of floors per thermal envelope are incorporated to compute the values shown in Table 9.
Outdoor weather conditions
Outdoor air properties and solar irradiation data are obtained from measurements conducted by the National Renewable Energy Laboratory (NREL) and the King Abdulaziz City for Science and Technology (KACST) (NREL and KACST 2014). The regional data are processed to obtain average hourly seasonal values for dry-bulb temperature, relative humidity, and solar direct normal irradiation (DNI). From the DNI data, the hourly total irradiation for the walls and roof is computed as the sum of direct, diffuse, and reflected irradiation. Furthermore, Weibull distributions of wind speeds by season and region were developed by Rehman et al. (1994). The Weibull mean values are used throughout the day for the sake of simplicity.
Indoor air properties and infiltration
The model computes the amount of energy required to meet some desirable indoor air conditions. ASHRAE Standard 55-2010, which was formed to determine indoor air properties that would achieve thermal comfort, is here used to specify the indoor dry-bulb air temperature based on the seasonal average outdoor air temperature. The indoor relative humidity is set between 45 to 55 %. The properties of the moist air flowing through the system are either calculated or taken from the literature (e.g., Moran and Shapiro 2004). It is assumed that residences have moderate infiltration rates, ranging from 0.65 to 0.90 air changes per hour (ACH) for traditional residences and between 0.55 to 0.90 ACH for villas and apartments.
Air-conditioner stock and performance
The residential stock of air conditioners in Saudi Arabia has almost exclusively been of the unitary type. Split-type and window air conditioners have a 97 % market share according to Saudi Aramco (2011). Based on the results of a survey conducted by AMAD for Technical Consultation and Laboratories (2011), the stock’s average EER for cooling is pegged around 7 BTU/(Wh). Also, these packaged units typically have a single indoor fan or blower as opposed to more than one fan in a centralized system with a duct network. We estimate that the specific fan power (SFP) is between 0.4 and 0.7 kW/(m3/s); a typical valueFootnote 1 of the SFP for unitary systems is around 0.5 kW/(m3/s). We make the assumption that space heating equipment has low usage nationwide.
Lighting
Estimated market shares of lighting technologies used in homes were derived from imports data published by the CDSI. Shown by Table 10, the dominant technologies used in residences are incandescent and linear fluorescent lamps. The estimated model inputs for average power ratings and efficacy for each technology are also shown.
Moreover, typical lighting requirements for casual activity range from 108 to 215 lm/m2 (Jefferis and Jefferis 2013). These values, in conjunction with envelope geometry, are used to estimate the number of light bulbs installed in residences. It is unlikely that all light bulbs would be turned on simultaneously, and it is therefore assumed that 40 % of the bulbs are contributing to the load during times of use.
The usage times of indoor lighting are specified such that lights are turned on from sunset to 10 PM. Outdoor lighting, which alternatively does not contribute to the internal heat gain and is represented by two incandescent lamps per archetype, is specified to be on from sunset until sunrise. The model determines sunset and sunrise times using the trigonometric relationships applied for calculating solar irradiation. The amount of electricity directly consumed by lighting is calibrated against the value of 6.13 TWh reported by Faruqui et al. (2011).
Appliances
The relevant data inputs for household appliances are their level of stock, performance characteristics, and times of use. The saturation level, here defined as the number of units per household, is the measure used to quantify stock. The saturation of consumer electronics, which are comprised of computers, televisions, gaming consoles, smart phones, and set-top disk players, is reported by the Dubai Press Club (2012). Applying an assumption that the lifetime of household appliances is around 8 years, the saturation levels for other appliances are estimated using the imports data from 2003 to 2011 published by the CDSI. Al-Shaikh (2003) indicated that 65 % of the domestic demand for durable consumer goods is met by imports.
There are no time-use and appliance power ratings data for Saudi households. For the sake of being straightforward, the fraction of households using discretionary appliances is distributed evenly across all hours of the day when household members are typically awake. Non-discretionary uses like those of the refrigerator and freezer run continuously throughout the year. The power ratings of the appliances are estimatedFootnote 2 such that their total annual electricity consumption matches the amount detailed by Faruqui et al. (2011). Table 11 shows the calculated model inputs for appliance saturation and power ratings.
Windows
We estimate that all walls of the envelope have windows that take up 15 % of their surface area. In the calibration, all windows are single-glazed with moderate internal shading and no external shading. The associated solar transmittance properties are obtained from McQuiston et al. (2005). The overall heat transfer coefficient used is 1 W/(m K) and the diffuse solar transmittance is 0.75. The direct solar transmittance is a function of the solar angle of incidence on a surface of a particular orientation. The applied convective fraction of the conduction heat gain through the windows is 0.37.
AHU supply air
The air is supplied at different temperatures depending on whether cooling or heating is required. It is assumed that air is supplied at 10 to 12 °C below the desired indoor air temperature for cooling, and at 17 °C above the desired indoor air temperature when heating. The humidity ratio of the supply air is specified between 5 and 7.5 g of moisture/kg of air for cooling and 10.5 g of moisture/kg for heating. These are reasonable values for HVAC design. The analysis does not allow for any ventilation air to be drawn in from outside in all situations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made.
The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
To view a copy of this licence, visit https://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Matar, W. Beyond the end-consumer: how would improvements in residential energy efficiency affect the power sector in Saudi Arabia?. Energy Efficiency 9, 771–790 (2016). https://doi.org/10.1007/s12053-015-9392-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12053-015-9392-9