Measuring persistent and transient energy efficiency in the US

Abstract

The promotion of US energy efficiency policy is seen as a very important activity. Generally, the level of energy efficiency of a country or state is approximated by energy intensity, commonly calculated as the ratio of energy use to GDP. However, energy intensity is not an accurate proxy for energy efficiency given that changes in energy intensity are a function of changes in several factors including the structure of the economy, climate, efficiency in the use of resources, behaviour and technical change. The aim of this paper is to measure persistent and transient energy efficiency for the whole economy of 49 states in the US using a stochastic frontier energy demand approach. A total US energy demand frontier function is estimated using panel data for 49 states over the period 1995 to 2009 using two panel data models: the Mundlak version of the random effects model (which estimates the persistent part of the energy efficiency) and the true random effects model (which estimates the transient part of the energy efficiency). The analysis confirms that energy intensity is not a good indicator of energy efficiency, whereas, by controlling for a range of economic and other factors, the measures of energy efficiency obtained via the approach adopted here are. Moreover, the estimates show that although for some states energy intensity might give a reasonable indication of a state’s relative energy efficiency, this is not the case for all states.

Introduction

The promotion of energy efficiency policies is seen as a major strand of energy policy in the US and across the globe given the need to reduce greenhouse gas emissions and maintain security of energy supply. It is therefore vital that in the US the true relative energy efficiency across the different states is clearly measured. However, generally a state’s energy efficiency is approximated by energy intensity—commonly calculated as the ratio of energy use to GDP (or approximated by energy productivity—the inverse of the energy intensity). Nonetheless, these two indicators, energy intensity and energy productivity, are not good proxies for energy efficiency because changes in both indicators are a function of changes in several factors including the structure of the economy, the level of production, climate, the level of efficiency in the use of resources and technical change. For example, EC (2000, p. 3) recognises that ‘Changes in energy intensity for final energy consumption are a first and rough estimate indicator for changes in energy efficiency’, and the US Energy Information Agency came to a similar conclusion.¹ Therefore, a decrease in energy intensity or an increase in energy productivity of a state does not necessarily imply that the efficiency in the use of energy in the state has increased.

Given the problems with the proxy measures, different approaches have been proposed in the academic literature that attempt to identify the change in the true level of efficiency in the use of energy at the aggregate economy level.² One approach proposed by Bossanyi (1979) and Myers and Nakamura (1978) is based upon Index Decomposition Analysis (IDA). This makes use of several types of index numbers and is achieved by decomposing the changes in energy intensity into the change in fuel mix, the change in the structure of the economy and what they regard as the actual change in energy efficiency.³ Moreover, some studies using IDA propose an additional step of the empirical analysis to identify, using an econometric approach, the determinants of the variation over time and across regions of energy intensity. For instance, Metcalf (2008) decomposed US state aggregate energy intensity for the period 1970–2001 and attempted econometrically to identify the determinants of the changes in intensity, efficiency and activity indexes.⁴

Another approach is based on the concept of productive efficiency and input specific technical efficiency introduced by Farrell (1957) and Kopp (1981) and can be used for estimating production, cost, distance or input demand frontier functions. From the economics point of view, it is important to produce energy services in an efficient way; that is, by minimising the amount of inputs used in the production of a given energy service, by choosing the combination of inputs that minimise the production cost and by adopting the least cost technology. A reduction in energy consumption for the production of energy services can come about by an improvement of the level of the efficiency in the use of inputs (productive efficiency), by an adoption of a new energy saving technology or by both processes. A theoretical explanation of this approach was originally introduced by Huntington (1994) and developed in Filippini and Hunt (2015). Zhou and Ang (2008), Filippini and Hunt (2011) and Lin and Du (2013) are examples of empirical applications that have attempted to use frontier analysis methods that have been developed in applied production theory. These recognise (albeit implicitly in some cases) that, in order to analyse the level of (energy) efficiency, it is important to base the analysis on a theoretical framework that regards energy as an input into a production function for producing an energy service (such as heating and lighting). It is therefore believed that this latter approach, which is advocated in this paper, is more suitable for performing an economic analysis of energy efficiency (hereafter EE) given its theoretical foundation in the microeconomics of production.⁵

Frontier analysis can be undertaken by estimating either a non-parametric or a parametric best practice frontier for the use of energy, where the level of EE is computed as the difference between the actual energy use and the predicted energy use at the frontier. Zhou and Ang (2008) is an example of the non-parametric approach, where the EE performance of 21 OECD countries over 5 years (1997–2001) is measured using a Data Envelopment Analysis (DEA) model. However, Filippini and Hunt (2015) discuss in some detail three parametric approaches that can be used to estimate the level of efficiency in the use of energy: (1) the energy requirement function, (2) the Shephard energy distance function and (3) the energy demand frontier function. One example of applying the energy demand frontier function approach is Filippini and Hunt (2011)⁶ where they estimate a frontier whole economy aggregate energy demand function for 29 OECD countries over the period 1978 to 2006 using Stochastic Frontier Analysis (SFA).⁷ An example of applying the Shephard energy distance function is Lin and Du (2013) who analysis of the efficient use of energy across China’s 30 administrative regions over the period 1997 to 2010.⁸

This paper favours the use of the parametric energy demand frontier function approach as suggested in Filippini and Hunt (2015). It therefore builds on Filippini and Hunt (2011, 2012) by attempting to measure the efficiency of energy use for the whole economy of 49 states in the US.⁹ This produces a specific measure of EE by explicitly controlling for income and price effects, population, climate, household size, the structure of the economy and the underlying energy demand trend (UEDT).¹⁰ This is seen as important, given the need to isolate the true EE across the different states. This paper attempts therefore to unpick exactly what is meant by the term EE and re-couch it in terms of productive economic efficiency and inefficiency, the focus being on where consumers of energy and energy services are away from their economically optimal position on the isoquant (i.e. they are inefficient), and from this develop a measure of EE based on economic principles. Furthermore, using different frontier models for panel data enables the estimation of the persistent, as well as the transient, EE for the US states. The use of parametric frontier analysis for the estimation of the level of EE of an economic system seems to be a promising approach to solve, at least partially, some limitations of the simple measure such as energy intensity (hereafter EI). Of course, as discussed further in the paper, this approach also has some limitations that should be considered when interpreting the results.

The paper is organised as follows. The next section presents and discusses the rationale and specification of the energy demand frontier function followed by a section that discusses the data and econometric specification. The results of the estimation are presented in the penultimate section, with a summary and conclusion in the final section.

An aggregate frontier energy demand model

Energy is a derived demand, emanating from the demand for an energy service. A state’s total aggregate energy demand is therefore a demand derived from the demand for several energy services used in an economy, all of which are produced by combining capital, energy and labour. Consequently, in this context, aggregate total energy demand can be interpreted as a state’s input demand function. Therefore, following Filippini and Hunt (2011), it is assumed that there exists an aggregate energy demand relationship for a panel of states of the US, as follows¹¹:

$$ {E}_{it} = E\left({P}_{it,},\ {Y}_{it},PO{P}_{it},\ HD{D}_{it},\ CD{D}_{it},H{S}_{it},\ SH{I}_{it},\ SH{S}_t,{A}_i,\ UED{T}_{t,}E{E}_{it}\right) $$

(1)

where E _it is aggregate energy consumption, Y _it is GDP, P _it is the real price of energy, POP _it is population, HDD _it are the heating degree days, CDD _it are the cooling degree days, HS _it is the household size, SHI _it is the share of value added of the industrial sector and SHS _it is the share of value added for the service sector¹²; all for state i in year t. A _i is the geographical area size of each state, UEDT _t reflects a common UEDT across states capturing both exogenous technical progress and other exogenous factors. EE _it is the unobserved level of EE for state i in year t. Hence, a low level of EE implies an inefficient use of energy (i.e. waste energy), so that in this situation, awareness of energy efficiency could be increased in order to reach the optimal energy demand. Of course, an inefficient use of energy implies productive inefficiency, i.e. a non-optimal use of all inputs, not necessarily only of the energy input. Nevertheless, from an empirical perspective, the aggregate level of EE is not observed directly, but instead this indicator has to be estimated. Consequently, in order to estimate a state’s level of EE and identify the best practice state in terms of energy utilisation, the stochastic frontier function approach introduced by Aigner et al. (1977) is used. The level of precision when measuring the EE of each state using a stochastic frontier approach depends upon the type and number of variables included in the estimated specification like Eq. (1). Here, it is believed that the variables considered in Eq. (1)—those usually utilised in econometric studies of aggregate energy demand—represent, relatively well, the most important energy demand drivers.¹³

An aggregate input demand frontier function gives the minimum level of input used by an economy for any given level of output; hence, the difference between the observed input and the cost-minimising input demand represents both technically as well as allocative inefficiency.¹⁴ In the case of an aggregate total energy demand function, used here, the frontier gives the minimum level of energy consumption necessary for a state to produce any given level of energy services. This frontier approach allows the possibility to identify if a state is, or is not, on the frontier. Moreover, if a state is not on the frontier, the distance from the frontier measures the level of energy consumption above the baseline demand, e.g. the level of energy inefficiency.

The approach used in this study is therefore based on the assumption that the level of energy inefficiency of a state’s whole economy can be approximated by a one-sided non-negative term, so that a panel log-log functional form of Eq. (1) adopting the stochastic frontier function approach proposed by Aigner et al. (1977) can be specified as follows:

$$ {e}_{it}=\alpha +{\alpha}^p{p}_{it}+{\alpha}^y{y}_{it}+{\alpha}^{pop}po{p}_{it}+{\alpha}^{hs}h{s}_{it}+{\alpha}^{hdd}hd{d}_{it}+{\alpha}^{cdd} cd{d}_{it}+{\alpha}^{SHI}SH{I}_{it}+{\alpha}^{SHS}SH{S}_{it}+{\alpha}^a{a}_i+{\alpha}^tt+{v}_{it}+{u}_{it} $$

(2)

where e _it is the natural logarithm of aggregate energy consumption (E _it ), p _it is the natural logarithm of the real price of energy (P _it ), y _it is the natural logarithm of GDP (Y _it ), pop _it is the natural logarithm of population (POP _it ), hdd _it is the natural logarithm of the heating degree days (HDD _it ), cdd _it is the natural logarithm of the cooling degree days (CDD _it ), hs _it is the natural logarithm of the household size (HS _it ), a _i is the natural logarithm of the area size (A _i ) and t is a time trend that proxies the UEDT.¹⁵ SHI _it and SHS _it are as defined above. Furthermore, the error term in Eq. (2) is composed of two independent parts. The first part, v _it , is a symmetric disturbance capturing the effect of noise and as usual is assumed to be normally distributed. The second part, u _it , which reflects the level of EE _it in Eq. (1), is interpreted as an indicator of the inefficient use of energy, e.g. the waste energy. It is a one-sided non-negative random disturbance term that can vary over time, assumed to follow a half-normal distribution.¹⁶ A more efficient use of energy will increase a state’s EE. The impact of technological and organisational innovation in the production and consumption of energy services on energy demand is therefore captured in a number of ways, including through the price term and the time trend. For instance, a rise in energy prices with a negative price elasticity and a negative coefficient of the time trend both suggest that energy saving technologies would be adopted over time, thus allowing states to decrease, ceteris paribus, their energy consumption. The model specification therefore allows on one side for states to modify their energy demand by adopting new energy saving technologies and on the other side by improving the level of efficiency in the use of energy (and the other inputs).

In summary, Eq. (2) is estimated in order to estimate EE for each state in the sample. The data and the econometric specification of the estimated equations are discussed in the next section.

Data and econometric specification

The study is based on a balanced US panel data set for a sample of 49 states (i = 1, …, 49) over the period 1995 to 2009. For the purposes of this paper, attention is restricted to the contiguous states (i.e. Alaska and Hawaii are excluded), whereas the District of Columbia is included and considered as a separate ‘state’. The data set is based on information from the US Energy Information Administration (EIA) database called States Energy Data System, from the US Department of Commerce, the US Census Bureau and the National Climatic Data Center at NOAA.

E _it is each state’s aggregate total energy consumption for each year in trillion BTUs, Y _it is each state’s real GDP for each year in thousand US 2010$ and P _it is each state’s real energy price for each year in per million BTUs 2010$. Total energy consumption figures and prices are from the EIA. Population (POP _it ) and GDP are from the Bureau of Economic Analysis of the US Census Bureau. The heating and cooling degree days (HDD _it and CDD _it ) are obtained from the National Climatic Data Center at NOAA. ¹⁷ The data on area size (A _i ) and household size, the number of people per household (HS _it ) are collected from the U.S. Census Bureau. Descriptive statistics of the key variables are presented in Table 1.

Table 1 Descriptive statistics

There are a number of different SFA model specifications using panel data that could be considered suitable for the task at hand.¹⁸ These include the basic models for panel data: the pooled model (PM), the random effects model (REM), the true fixed effects model (TFEM) and the true random effects model (TREM). Furthermore, as shown by Farsi et al. (2005) and by Filippini and Hunt (2012), it is possible to estimate some of these models using an adjustment introduced by Mundlak (1978) in order to account for the econometric problem of unobserved heterogeneity bias, such as the Mundlak adjusted pooled model (MPM) and the Mundlak adjusted random effects model (MREM). This adjustment attempts to separate the unobserved variables from inefficiency. Moreover, within this suite of models, some (such as the REM and the MREM) attempt to provide information on the persistent (time-invariant) part of inefficiency, whereas others (such as the TFEM and the TREM) attempt to provide information on the transient (time-varying) part of inefficiency.¹⁹ However, the distinction between transient and persistent efficiency has only recently been introduced in the literature; hence, for this reason, previous studies that have attempted to estimate EE, such as Filippini and Hunt (2011, 2012) and Lin and Du (2013), do not make this distinction.

All these models have their relative advantages and disadvantages, and the choice of model is not straightforward: it depends upon the goal of the exercise and the type of data and variables that are available. The PM is the SFA model in its original form proposed by Aigner et al. (1977) and adapted for panel data by Pitt and Lee (1981). This model does not exploit the possibility given by panel data to control for unobserved heterogeneity variables that are constant over time. Therefore, the unobserved heterogeneity bias can be a serious problem in this model. On the contrary, the REM introduced by Pitt and Lee (1981) interprets the typical panel data individual random effects as inefficiency rather than unobserved heterogeneity as in the traditional literature on panel data econometric methods.²⁰ The level of efficiency estimated with the REM does not vary over time. Therefore, this model arguably provides information on the persistent part of efficiency in the use of energy. One problem with the REM is that any unobserved, time-invariant, group-specific heterogeneity is considered as inefficiency and the level of efficiency does not vary over time. However, as shown in Farsi et al. (2005), the application of Mundlak’s adjustment to the REM frontier framework decreases the bias in inefficiency estimates by separating inefficiency from unobserved heterogeneity. This separation of inefficiency from unobserved heterogeneity is based on the assumption that the effects of unobserved time-invariant state characteristics are captured by the coefficients of the group mean of the explanatory variables of the Mundlak adjustment equation.

Greene (2005a, b) proposed the TFEM and the TREM whereby the PM is extended by adding fixed and random individual effects, respectively. The TFEM and the TREM are able to distinguish time-invariant unobserved heterogeneity from the time-varying level of efficiency component (the transient part). However, in these models, any time-invariant or persistent component of inefficiency is completely absorbed in the state-specific constant terms. Therefore, in contexts characterised by persistent inefficient use of energy determined for instance by the presence in a country of old houses or of an urban planning system that does not minimise the travel time, this provides relatively high levels of estimated transient EE.

Given this discussion, the MREM is seen as the appropriate approach to estimate the persistent part of the level of EE, and the TREM the appropriate approach to estimate the transient part of the level of EE.²¹ Consequently, in order to obtain estimates of both the persistent and transient parts of the inefficiency for the 49 states in the US, these two separate models, the MREM and the TREM, are estimated here and the two estimated values of inefficiency are interpreted accordingly.²² Of course, because the two models are measuring a different component of the level of EE, it is not expected to obtain similar rankings from these models. Table 2 summarises the two models.

Table 2 Econometric specifications of the stochastic cost frontier

After Eq. (2) is estimated, it is possible to estimate a state’s efficiency using the conditional mean of the efficiency term E[u _it |u _it  + v _it ] proposed by Jondrow et al. (1982), and the level of EE can be expressed by:

$$ E{E}_{it}=\frac{E_{it}^F}{E_{it}}= \exp \left(-{\widehat{u}}_{it}\right) $$

(3)

where E _it is the observed energy consumption and E ^F _it is the frontier or minimum demand of the ith state in time t. An EE score of one indicates a state on the frontier (100 % efficient), while non-frontier states, e.g. states characterised by a level of EE lower than 100 %, receive scores below one. This therefore gives the measures of EE estimated below.²³ In summary, Eq. (2) is estimated using the MREM and TREM, and for each of these, Eq. (3) is used to estimate the respective persistent and transient EE for each state for each year. Moreover, as previously discussed, it is expected that, compared to the estimated persistent EE, the level of the transient EE would be relatively high but with a lower variation. The results from the estimation are given in the next section.

Estimation results

The estimation results of the frontier energy demand models using the two models discussed above are given in Table 3.²⁴ Most of the estimated coefficients²⁵ and lambda ²⁶ have the expected signs and are statistically significant at the 10 % level and, generally, the results obtained in the two models are relatively similar. The results suggest that the variables included in the model are pertinent and explain most of the variation in aggregate energy demand across both state and time.²⁷

Table 3 Estimated coefficients (t ratios in parentheses)

The results suggest that US total energy demand is price inelastic, with the estimated elasticity being statistically significant from zero but relatively low at about −0.07. The results also suggest that US total energy demand is income inelastic, with an estimated elasticity of about 0.5. For the weather variables, the estimated heating degree-day elasticity has the expected sign and is significant, whereas the coefficient of the CDD variable is not significantly different from zero; similarly, the AREA coefficient is not significant in the MREM. The estimated household size elasticities are significant however and, as expected, are negative (both being close to −1) suggesting that an increase of 10 % in the household size decreases energy consumption by approximately 10 %. This decrease is probably due to economies of scale in the production of some residential energy services; for instance, the size of a fridge is unlikely to vary proportionally with the number of household members.

The estimated coefficients of the share of the industrial sector and of the service sector suggest a negative impact of these two variables on US total energy demand (noting that the reference sector is agricultural and mining). The coefficient of the time trend variable is negative and significant in both models, suggesting that energy-saving technical progress dominates other exogenous factors with an inward shift of the energy demand function over time. Finally, in the MREM, half of the included Mundlak terms are significant (note that in order to avoid multicollinearity between these mean variables and the original variables, a subset only of the variables are introduced for the Mundlak adjustment).²⁸

Table 4 provides descriptive statistics for the overall US EE estimates for the 49 states obtained from the econometric estimation. As discussed previously, the MREM provides information on the persistent level of inefficiency, whereas the TREM provides information on the transient part of efficiency. Nevertheless, it should be noted that although the persistent EE estimated by the MREM is time invariant, it does not mean that the model constrains states from using less energy by adopting new technologies over time given the inclusion of the UEDT in the form of a time trend with an estimated negative coefficient.

Table 4 Summary of EE estimates across all states, 1995–2009

Table 4 shows that, as expected, the estimated transient part of EE is higher than the persistent part, but the variation in the estimated transient EE is somewhat lower than the variation in the estimated persistent EE. In fact, the level of estimated transient efficiency is very similar for all states, all being very close to the average of 96 %; consequently, the ranking obtained from these estimates is not that informative. However, as stated above, there is far greater variation across states in the level of estimated persistent efficiency—hence, for the remainder of this paper, the focus is on the estimated persistent EE from the MREM.

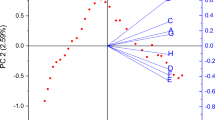
As discussed in Filippini and Hunt (2011, 2012), it is expected that estimated EE would be negatively correlated with EI; thus, for most states, it is expected that the level of EI decreases with an increase of the estimated level of EE. However, as Filippini and Hunt (2011) argue, if this technique were to be a useful tool for teasing out the true EE, then a perfect, or even near perfect, negative correlation would not be expected since all the useful information would be contained in standard EI measures. This proves to be the case with the estimates here, as illustrated in Fig. 1 with the correlation coefficient between average EI and average estimated persistent EE from the MREM being only −0.46. Furthermore, there is not a strong correlation between the rankings, with the Spearman rank correlation coefficient between average EI and average estimated persistent EE from the MREM being only 0.18.²⁹

Fig. 1

Scatter diagram of average EI and estimated persistent EE (1995–2009). AL Alabama, AZ Arizona, AR Arkansas, CA California, CO Colorado, CT Connecticut, DE Delaware, DC District of Columbia, FL Florida, GA Georgia, ID Idaho, IL Illinois, IN Indiana, IA Iowa, KS Kansas, KY Kentucky, LA Louisiana, ME Maine, MD Maryland, MA Massachusetts, MI Michigan, MN Minnesota, MS Mississippi, MO Missouri, MT Montana, NE Nebraska, NV Nevada, NH New Hampshire, NJ New Jersey, NM New Mexico, NY New York, NC North Carolina, ND North Dakota, OH Ohio, OK Oklahoma, OR Oregon, PA Pennsylvania, RI Rhode Island, SC South Carolina, SD South Dakota, TN Tennessee, TX Texas, UT Utah, VT Vermont, VA Virginia, WA Washington, WV West Virginia, WI Wisconsin, WY Wyoming

This is further highlighted in Fig. 2 that ranks the states in terms of the estimated persistent EE and EI and classifies the states into three groups: relatively efficient states, relatively inefficient states and relatively moderately efficient states. Although the states are ranked in Fig. 2, arguably the best way to consider the results from such a SFA estimation is in the groups as shown in Fig. 2 given that some of the states’ estimated persistent EE differ by very little.³⁰ Nonetheless, based on the groupings, Fig. 2 shows that EI would appear to be a good predictor of a state’s relative EE for some states but a very poor indicator for others. For example, Kansas, Louisiana, Maine, Mississippi, Montana, New Mexico, North Dakota, Ohio, Oklahoma, South Dakota, Texas and Wyoming are classified as being relatively inefficient states according to the estimated EE and are states with relatively high levels of EI. At the other end of the spectrum, the District of Columbia and Florida are classified as being relatively efficient states according to the estimated EE and are states with relatively low levels of EI. However, California, Connecticut, Delaware, Massachusetts, Maryland, New Hampshire, New York and Nevada are classified as being relatively inefficient states according to the estimated EE but are states with relatively low levels of EI. In addition, Idaho, Indiana, Michigan, Utah and Wisconsin are classified as being relatively efficient states according to the estimated EE but are states with relatively low levels of EI.

Fig. 2

Average EI and estimated persistent EE (1995–2009). a EI (1000 BTU per 2010US$). b Estimated persistent EE (from the MREM)

Within these results, it is worth highlighting California, which is found to be relatively inefficient according to the estimated persistent EE estimates. This would appear to be at odds with the conventional wisdom of policymakers and professionals who generally regard California as being a highly energy efficient state as well as a number of research papers such as Howrowitz (2007) and Sudarsham (2013). This view is normally based on EI or electricity intensity, so a direct comparison with the analysis here is difficult if not impossible given the whole premise of the EE measure estimated here that analysis based on EI is potentially biased and misleading for policymakers. Thus, the research presented here does not necessarily disagree with some of the previous research such as Howrowitz (2007, p. 93) who argues that ‘California’s energy efficiency programs … have dramatically reduced state electricity intensity’. It is just that if the analysis here is to be believed, there is still more to be done in order for California to increase its EE and move closer to the energy demand efficient frontier. ³¹ Furthermore, the work here supports the conclusion by Sudarshan (2013, p. 207) who contends that ‘while indices such as energy intensities … can provide a great deal of insight, they also hide as much as they reveal’. However, it should be noted that the proposed EE measure estimated here could be sensitive to the assumptions adopted regarding the econometric approach and model specification, so further validation and exploration is needed. Furthermore, the estimated measure of EE obtained using a stochastic frontier approach should be seen as providing a broad approximation of the direction of the true level of EE rather than an exact number and rank.

Summary and conclusion

Building on Filippini and Hunt (2011, 2012), this research attempts to define and estimate EE for 49 US states by combining energy demand modelling and frontier analysis. The energy demand specification controls for income, price, population, household size heating degree days, cooling degree days, the area, the share of the industrial sector, the share of the service sector and a UEDT and is estimated using the MREM and the TREM. These two models are seen as interesting techniques for attempting to uncover the general relative levels of the true EE of the 49 states and are regarded, given the current state of knowledge, as being superior to the range of other techniques available. Moreover, they avoid the problem of unobserved heterogeneity. Of course, future research on the level of EE of the US states could attempt to apply the recently developed econometric estimator that should be available soon whereby estimates of both persistent as well as transient efficiency can be obtained from one model (see Filippini and Greene 2015) at both the aggregate and sectoral level.

The estimates show that for some states, the simple measure of EI might give a reasonable indication of a state’s relative EE, but this is not so for other states, California being a good example. Therefore, unless the analysis advocated here is undertaken, US policy makers are likely to have a misleading picture of the true relative EE across the states and thus might make misguided decisions when allocating funds to various states in order to implement EE measures. Hence, it is argued that this analysis should also be undertaken in order to give US policy makers an additional indicator other than the rather naïve measure of EI in order to try to avoid potentially misleading policy conclusions. That said, it is recognised that the application of stochastic frontier analysis for estimating the level of EE is still a relatively new approach that requires further work and validation and is likely to be improved in future research. Thus, it is not being advocated that the measure of EE obtained using a stochastic frontier approach should be used in a mechanical way to produce rankings. However, at this stage at least, it is suggested that policy makers could use this as an additional alternative to just using the proxy measure, EI, and thus provide a general guide to the relative levels of EE, rather than an exact number and rank. In other words, the results from such analysis could be used as an additional instrument for regulatory decisions.