Rough interval approach to predict uncertain demand in a large scale disaster scenario: an analytical study on Assam flood

Abstract

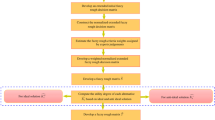
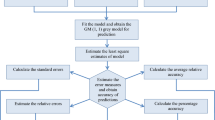
Disaster response operation is required to execute in unforeseen calamitous event. This research has designed a mathematical model for solid transportation problem in disaster response to allocate relief materials in the affected areas. Minimization of total cost for disaster operation and maximization of coverage of number of affected people to serve are two main objective functions of the model. The model is considered in two environments: certain and uncertain. To handle the uncertainty, this model is solved through three different techniques namely decomposition of interval-coefficient, expected value operator and rough chance constraint programming considering the parameters are in rough interval form. To measure the efficiency of proposed model, a real-life problem is performed considering the flood of Assam and a plan is envisaged for large-scale flood. Weighted metric method is used to convert multi-objective problem to single objective problem. The said model in certain environment gives optimal result in crisp form. In uncertain measure, solutions of the model are in the form of rough interval, crisp and interval which help concern authority to make better decision for allocating relief materials in disaster. Eventually, a comparative study is performed.

Appendices

Appendix I. Primary ideas about rough interval

Since the mathematical model proposed in the manuscript is a multi-objective solid transportation problem (MOSTP) with uncertainty and RI deals the uncertainty of the matheatical model, therefore it is required to explain some basic concept of the rough interval and rough set theory. This section brings the basic ideas and concepts of the theory related to the rough set along with interval co-efficient.

• 1. Rough set: Pawlak [7] defines rough set as approximation of a crisp set in terms of two sets: lower and upper approximation set.

• 2. Rough interval: Rebolledo [64] introduced RI which is a particular case of rough set including the lower approximation (LA) and upper approximation (UA). The qualitative value A is a rough interval when two close intervals $A_{*}$ and $A^{*}$ are assigned to it on R where $A_{*}$ $\subseteq$ $A^{*}$ [65]. Moreover, (i) If x $\in$ $A_{*}$ then A surely takes x. (ii) If x $\in$ $A^{*}$ then A possibly takes x. (iii) If x $\notin$ $A^{*}$ then A surely does not takes x.    $A_{*}$ and $A^{*}$ are known as LAI and UAI of A, respectively and A is denoted by A = ($A_*$,$A^*$). Note that the intervals $A_*$ and $A^*$ are not complement to each other.

• 3. Expected value of RI [66]:    Let X be an event expressed by {x: $\xi$(x)$\in$ B} where $\xi$ is a function from universe U to real line R, B $\subseteq$ R; and X is approximated by ($\underline{X}$; $\overline{X}$) according to the similarity relation R. Then the lower expected value of X is defined as $\underline{E}$[$\xi$]=$\int \nolimits _0^{+\infty }$ $\underline{Appr}${$\xi$ $\ge$ r}dr-$\int \nolimits _{-\infty }^0$ $\underline{Appr}${$\xi$ $\le$ r}dr, where $\underline{Appr}$(X)= $\frac{\left| X\cap \underline{X}\right| }{\underline{X}}$ and the upper expected value of X is defined as $\overline{E}$[$\xi$]=$\int \nolimits _0^{+\infty }$ $\overline{Appr}${$\xi$ $\ge$ r}dr-$\int \nolimits _{-\infty }^0$ $\overline{Appr}${$\xi$ $\le$ r}dr, where $\overline{Appr}$(X)=$\frac{\left| X\right| }{\overline{X}}$. Hence the expected value of X is defined as E[$\xi$]=$\int \nolimits _0^\infty$Appr{$\xi$ $\ge$ r}dr-$\int \nolimits _\infty ^0$Appr{$\xi$ $\le$ r}dr. Relation between lower expected, upper expected and expected value of an event X is defined with the help of following proposition.

Proposition

[66] Let X be an event expressed by {x: $\xi$ $\in$ B} where $\xi$ is a function from universe U to real line R, B $\subseteq$ R; and X is approximated by ($\underline{X}$; $\overline{X}$) according to the similarity relation R and and $\eta$ is a given parameter predetermined by the DM preference. Then E(X)=$\eta$ $\underline{E}$(X)+(1-$\eta$)$\overline{E}$(X)

Proof

Refer to [66] $\square$

Theorem

Let A=([a,b],[c,d]) where($c \le a \le b \le d$) be a RI. Then the expected value of A is $\frac{1}{2}$[$\eta$(a+b)+(1-$\eta$)(c+d)].

Proof

Refer to [66]

Remark

If $\eta$= 0.5 then the expected value of E[([a,b];[c,d])]= $\frac{1}{4}$(a+b+c+d).

• 4. Trust measure of RI: [67]: Let A=($A_*, A^*$) be a rough value on the approximation space. Then the lower trust measure of the rough event A $\le$ r is defined by $Tr_* \{A \le r\}= \frac{Card (y\in A_*|y\le r)}{Card (A_*)}$. Where Card() denotes the cardinal number of a given set. Similarly the upper trust measure is defined by $Tr^* \{A \le r\}= \frac{Card (y\in A^*|y\le r)}{Card (A^*)}$. The trust measure of the rough event is given by $Tr_* \{A \le r\} = \frac{1}{2} (Tr_*\{A \le r\}+ Tr^*\{A \le r\})$. The trust may be defined as any convex combination of the lower and upper trusts [67]. Let $\xi = ([\underline{a}^l, \underline{a}^u],[\overline{a}^l, \overline{a}^u])$ be a RI, then trust measure of a rough event $\xi \le r$ and trust is defined as:

  $$Trust\{\xi \le r\}= \left\{ \begin{array}{ll} 0 &{} {\text{if}} \,\, r \le {\overline{a}}^{l},\\ \frac{1}{2}(\frac{{\overline{a}}^{l-r}}{{\overline{a}}^{l}-{\overline{a}}^{u}}) &{} {\text{if}} \,\, {\overline{a}}^{l} \le r \le {\underline{a}}^{l},\\ \frac{1}{2}(\frac{{\overline{a}}^{l-r}}{{\overline{a}}^{l}-{\overline{a}}^{u}}+(\frac{{\underline{a}}^{l-r}}{{\underline{a}}^{l}-{\underline{a}}^{u}} )&{} {\text{if}} \,\, {\underline{a}}^{l} \le r \le {\underline{a}}^{u},\\ \frac{1}{2}(\frac{{\overline{a}}^{l-r}}{{\overline{a}}^{l}-{\overline{a}}^{u}}+1) &{} {\text{if}} \,\, {\underline{a}}^{u} \le r \le {\overline{a}}^{u},\\ 1 &{} {\text{if}} \,\, r \ge {\overline{a}}^{u}.\\ \end{array} Trust\{\xi \ge r\}= \left\{ \begin{array}{ll} 0 &{} {\text{if}} \,\, r \ge {\overline{a}}^{u},\\ \frac{1}{2}(\frac{{\overline{a}}^{u-r}}{{\overline{a}}^{u}-{\overline{a}}^{l}}) &{} {\text{if}} \,\, {\underline{a}}^{u} \le r \le {\overline{a}}^{u},\\ \frac{1}{2}(\frac{{\overline{a}}^{u-r}}{{\overline{a}}^{u}-{\overline{a}}^{l}}+(\frac{{\underline{a}}^{u-r}}{{\underline{a}}^{u}-{\underline{a}}^{l}} )&{} {\text{if}} \,\, {\underline{a}}^{l} \le r \le {\underline{a}}^{u},\\ \frac{1}{2}(\frac{{\overline{a}}^{u-r}}{{\overline{a}}^{u}-{\overline{a}}^{l}}+1) &{} {\text{if}} \,\, {\underline{a}}^{l} \le r \le {\overline{a}}^{l},\\ 1 &{} {\text{if}} \,\, r \le {\overline{a}}^{u}.\\ \end{array} \right. \right. $$

  α-optimistic value is given by,

  $$\xi _{sup}(\alpha )= \left\{ \begin{array}{ll} (1-2\alpha )\overline{a}^u+2\alpha \overline{a}^l, &{} {\text{if}} \,\,\, \alpha \le \frac{\overline{a}^u-\underline{a}^u}{2(\overline{a}^u-\overline{a}^l)}\\ 2(1-\alpha )\overline{a}^u+(2\alpha -1)\overline{a}^l, &{} {\text{if}} \,\,\, \alpha \ge \frac{2\overline{a}^u-\underline{a}^l-\overline{a}^l}{2(\overline{a}^u-\overline{a}^l)}\\ \frac{\overline{a}^u(\underline{a}^u-\underline{a}^l)+\underline{a}^l(\overline{a}^u-\overline{a}^l)-2\alpha (\underline{a}^u-\underline{a}^l)(\overline{a}^u-\overline{a}^l)}{(\underline{a}^u-\underline{a}^l)+(\overline{a}^u-\overline{a}^l)}, &{} {\text{otherwise}} \end{array} \right. $$

  α- pessimistic value is given by,

  $$\xi _{inf}(\alpha )= \left\{ \begin{array}{ll} (1-2\alpha )\overline{a}^l+2\alpha \overline{a}^u, &{} {\text{if}} \,\,\, \alpha \le \frac{\underline{a}^l-\overline{a}^l}{2(\overline{a}^u-\overline{a}^l)}\\ 2(1-\alpha )\overline{a}^l+(2\alpha -1)\overline{a}^u, &{} {\text{if}} \,\,\, \alpha \ge \frac{\underline{a}^u+\overline{a}^u-2\overline{a}^l}{2(\overline{a}^u-\overline{a}^l)}\\ \frac{\overline{a}^u(\underline{a}^u-\underline{a}^l)+\underline{a}^l(\overline{a}^u-\overline{a}^l)+2\alpha (\underline{a}^u-\underline{a}^l)(\overline{a}^u-\overline{a}^l)}{(\underline{a}^u-\underline{a}^l)+(\overline{a}^u-\overline{a}^l)}, &{} {\text{otherwise}} \end{array} \right. $$

Appendix II. Remarks

Some sequential order of the interval co-efficients of RI are given below:

$[\underline{t}_{ijpk}^{l},\underline{t}_{ijpk}^{u}] \subseteq [\overline{t}_{ijpk}^{l},\overline{t}_{ijpk}^{u}] \Rightarrow \overline{t}_{ijpk}^{l} \le \underline{t}_{ijpk}^{l} \le \underline{t}_{ijpk}^{u} \le \overline{t}_{ijpk}^{u}$

$[\underline{c}_p^{l},\underline{c}_p^{u}] \subseteq [\overline{c}_p^{l},\overline{c}_p^{u}] \Rightarrow \overline{c}_p^{ l} \le \underline{c}_p^{l} \le \underline{c}_p^{u} \le \overline{c}_p^{u}$

[$\underline{a}$ $_{ip}^{ l}$,$\underline{a}$ $_{ip}^{ u}$]$\subseteq$[$\overline{a}$ $_{ip}^{ l}$,$\overline{a}$ $_{ip}^{ u}$]$\Rightarrow$ $\overline{a}$ $_{ip}^{ l}$ $\le$ $\underline{a}$ $_{ip}^{ l}$ $\le$ $\underline{a}$ $_{ip}^{ u}$ $\le$ $\overline{a}$ $_{ip}^{ u}$

[$\underline{b}$ $_{jp}^{ l}$,$\underline{b}$ $_{jp}^{ u}$]$\subseteq$[$\overline{b}$ $_{jp}^{ l}$,$\overline{b}$ $_{jp}^{ u}$]$\Rightarrow$ $\overline{b}$ $_{jp}^{ l}$ $\le$ $\underline{b}$ $_{jp}^{ l}$ $\le$ $\underline{b}$ $_{jp}^{ u}$ $\le$ $\overline{b}$ $_{jp}^{u}$

[$\underline{W}$ $_k^{l}$,$\underline{W}$ $_k^{u}$]$\subseteq$[$\overline{W}$ $_k^{l}$,$\overline{W}$ $_j^{u}$]$\Rightarrow$ $\overline{W}$ $_k^{l}$ $\le$ $\underline{W}$ $_k^{l}$ $\le$ $\underline{W}$ $_k^{u}$ $\le$ $\overline{W}$ $_k^{u}$

[$\underline{V}$ $_k^{l}$,$\underline{V}$ $_k^{u}$]$\subseteq$[$\overline{V}$ $_k^{l}$,$\overline{V}$ $_j^{u}$]$\Rightarrow$ $\overline{V}$ $_k^{l}$ $\le$ $\underline{V}$ $_k^{l}$ $\le$ $\underline{V}$ $_k^{u}$ $\le$ $\overline{V}$ $_k^{u}$

[$\underline{s}$ $_{j}^{ l}$,$\underline{s}$ $_{j}^{u}$]$\subseteq$[$\overline{s}$ $_{j}^{ l}$,$\overline{s}$ $_{j}^{u}$]$\Rightarrow$ $\overline{s}$ $_{j}^{l}$ $\le$ $\underline{s}$ $_{j}^{l}$ $\le$ $\underline{s}$ $_{j}^{u}$ $\le$ $\overline{s}$ $_{j}^{u}$

[$\underline{B}$ $^{l}$,$\underline{B}$ $^{u}$]$\subseteq$[$\overline{B}$ $^{l}$,$\overline{B}$ $^{u}$]$\Rightarrow$ $\overline{B}$ $^{l}$ $\le$ $\underline{B}$ $^{l}$ $\le$ $\underline{B}$ $_j^{u}$ $\le$ $\overline{B}$ $^{u},$      $\forall$ i=1, 2, ...I, j=1, 2, ...J , k=1, 2, ...K, p=1, 2..P.