Abstract
A computerized mathematical procedure based on nonlinear programming is presented for the purpose of a sandy soil parameter prediction problem by inverse analysis. The task of inverse analysis is to evaluate the values of input parameters for a specified output or response of the system. This inverse problem to determine the values of system input parameters is mathematically formulated as a constrained optimization problem in this study. The input parameters are considered as design variables. The constraint set is developed through the implementation of lower and upper bound on design variables. The objective function is determined by evaluating the error or mismatch between the specified output (reference value) and the model predicted value for a given design vector. The resulting nonlinear programming problem is solved using the Interior Penalty Function method coupled with the Davidon-Fletcher-Powell method and quadratic interpolation scheme. To demonstrate the proposed methodology, two illustrative examples related to axially loaded piles installed in sandy soil medium are considered. The numerical results indicate that the back analyzed values are in good agreement with their respective reference values.





Similar content being viewed by others
Data Availability
Some or all data, models, or codes that support the findings of this study are available from the corresponding author upon reasonable request.
Abbreviations
- \(\vec{X}\) :
-
Vector of design variables
- \(f(\vec{X})\) :
-
Objective function
- \(g_{j} (\vec{X}) \le 0\) :
-
System constraint
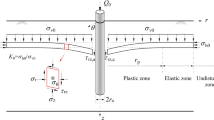
- \(Q_{ult}\) :
-
Ultimate load
- \(q_{sL}\) :
-
Limit unit shaft resistance
- \(q_{bL}\) :
-
Limit unit base resistance
- \(q_{b,10\% }\) :
-
Ultimate unit base resistance
- \(\sigma_{v}^{^{\prime}}\) :
-
Vertical effective stress
- \(K_{0}\) :
-
Coefficient of earth pressure at rest
- \(\phi_{c}\) :
-
Critical state friction angle
- \(D_{R}\) :
-
Relative density
- \(p_{A}\) :
-
Reference stress
- \(\sigma_{h}^{^{\prime}}\) :
-
Horizontal effective stress
- \(r_{k}\) :
-
Penalty parameter
- \(C\) :
-
Reduction factor
- \(S_{i}\) :
-
Search direction
- \(\lambda^{*}\) :
-
Optimum step length along the search direction
- \(\varepsilon\) :
-
Tolerance value
- \(\alpha\) :
-
Scale factor
- \(\gamma_{sat}\) :
-
Bulk unit weight of sandy soil
- \(\gamma_{w}\) :
-
Unit weight of water
References
Asaoka A and Matsuo M 1979 Bayesian approach to inverse problem in consolidation and its application to settlement prediction. In: Proceedings of Third International Conference on Numerical Methods in Geomechanics, Aachen, pp. 115–123
Fenelli G B and Galateri C 1981 Soil modulus for laterally loaded bored piles in pozzolana. In: Proceedings of Tenth International Conference on S.M. and F.E., Stockholm, 2, pp. 703–708
Arai K, Ohta H and Yasui T 1983 Simple optimization techniques for evaluating deformation moduli from field observations. Soils Found. 24(4): 95–108
Gioda G and Sakurai S 1987 Back analysis procedures for the interpretation of field measurements in geomechanics. Int. J. Numer. Methods Geomech. 11: 555–583
Desai C S, Pradhan S K and Cohen D 2005 Cyclic testing and constitutive modeling of saturated sand-concrete interfaces using the disturbed state concept. Int. J. Geomech. 5(4): 286–294
Yamagami T and Ueta Y 1987 Optimization techniques for back analysis of failed slopes. In: Proceedings of Eight Asian Regional Conference, Kyoto, 1, pp. 513–516
Suzuki H and Matsuo M 1988 Procedure of slope failure prediction during rainfall based on the back analysis of actual case records. Soils Found. 23(3): 51–63
Honjo Y, Limanhadi B and Wen-Tsung L 1993 Prediction of single pile settlement based on inverse analysis. Soils Found. 33(2): 126–144
Yi W-J and Xia L-Q 2015 Inverse analysis method for pseudo-dynamic test with pile-soil interaction. J. Hunan Univ. Nat. Sci. 42(5): 1–7
Adachi T and Kojima K 1989 Estimation of design parameters for earth tunnels. In: Proceedings of Twelve International Conference on S.M. and F.E., Riode Janeiro, 2, pp. 771–774
Xiao Y, Yin F, Liu H, Chu J and Zhang W 2017 Model tests on soil movement during the installation of piles in transparent granular soil. Int. J. Geomech. 17(4)
Gajetas G 1989 Shear modulus of rockfill from lateral pile load test. In: Proceedings of Twelve International Conference on S.M. and F.E., Riode Janeiro. 2, pp. 833–836
Ledesma A, Gens A and Ealonso E 1989 Probabilistic back analysis using a maximum likelihood approach. In: Proceedings of Twelve International Conference on S.M. and F.E., Riode Janeiro, 2, pp. 849–852
Shoji M, Ohta H, Matsumoto T and Morikawa S 1989 Safety control of embankment foundations based on elastic-plastic back analysis. Soils Found. 29(2): 112–126
Bhattacharya G 1990 Sequential unconstrained minimization technique in slope stability analysis. Ph.D. Thesis, Indian Institute of Technology, Kanpur, India
Bergado D T, Enriques A S, Sampaco C L, Alfaro M C and Balasubramaniam A S 1992 Inverse analysis of geotechnical parameters on improved soft Bangkok clay. J. Geotech. Eng. ASCE. 118(7): 1012–1030
Boonsinsuk P 1994 Back analysis of cut slope instability in soft Bangkok clay. In: Proceedings of International Conference on S.M. and F.E., Balkema, pp. 237–248
Venclik P 1994 Development of an inverse back analysis code and its verification. In: Numerical Methods in Geotechnical Engineering, ed. Smith, Balkema, Rotterdam. pp. 423–430
Gioda G 1990 Indirect identification of the average elastic characteristics of rock masses. In: International Conference on Structural Foundation on Rock, Sydney, pp. 65–73
Gioda G 1985 Some remarks on back analysis and characterization problems. In: 5th International Conference on Numerical Methods in Geomechanics, Nagoya, pp. 47–61
Warrington D C 2016 Improved methods for forward and inverse solution of the wave equation for piles. Ph.D. Thesis, The University of Tennessee, Chattanooga, United States
Honjo Y, Iwamoto S, Sugimoto M, Onimaru S and Yoshzawa M 1998 Inverse analysis of dynamic soil properties based on seismometer array records using the extended Bayesian method. Soils Found. 38(1): 131–143
Raju P 1999 Parameters estimation from in-situ pile load test results using non-linear programming and neural networks: an inverse analysis. Ph.D. Thesis, Indian Institute of Technology, Kanpur, India
Dey A and Basudhar P K 2012 Estimation of Burger model parameters using inverse formulation. Int. J. Geotech. Eng. 6: 261–274
Misra A 2010 A multicriteria based quantitative framework for assessing sustainability of pile foundations. M.S. Thesis, University of Connecticut, United States
Salgado R 2006 The Engineering of Foundation. McGraw-Hill, USA
Salgado R and Prezzi M 2007 Computation of cavity expansion pressure and penetration resistance in sands. Int. J. Geomech. 7(4): 251–265
Rao S S 2009 Engineering optimization: theory and practice. John Wiley & Sons, USA
Author information
Authors and Affiliations
Corresponding author
Appendix A
Appendix A
Mathematical method to solve a nonlinear programming (NLP) problem
A standard NLP problem may be defined as:
Determine a vector of design variables \(\vec{X}\) that minimizes the objective function \(f(\vec{X})\) satisfying the set of constraint
To solve the NLP problem, IPF based method coupled with the DFP method and QIM is used in this study. These three methods are used for the following purposes.
IPF: constrained optimization problem is converted into an equivalent unconstrained optimization problem.
DFP: minimizes the unconstrained problem.
QIM: calculation of optimum step length along the direction of search from a given point.
1.1 IPF method
Generate a new function \(\phi (\vec{X},r_{k} )\) as
where, rk is the positive constant (also called as penalty parameter). In the general initial value of rk is taken as such two terms in the right-hand side of equation (A2) are the same at the initial feasible design point \(\vec{X}_{0}\).
Starting value of penalty parameter
1.2 DFP method
For r = r1, \(\phi\) function is minimized beginning from the design point \(\vec{X}_{0}\) according to the DFP method. This involves the following steps:
-
(1)
At a point \(\vec{X}_{0}\), generate a direction of movement \(\vec{S}_{0}\) as
$$ S_{0} = - \left[ {H_{0} } \right]\nabla \phi_{0} $$(A4)
[H0] is an initial symmetric positive definite matrix. Initially, it may be assumed as an identity matrix. \(\nabla \phi_{0}\) is gradient vector of \(\phi\) function calculated at \(\vec{X}_{0}\). \(S_{0}\) is known as the direction of search vector evaluated at \(\vec{X}_{0}\).
-
(2)
Determine a new vector \(\vec{X}_{i + 1}\) as
$$ \vec{X}_{i + 1} = \vec{X}_{i} + \lambda_{i}^{*} \vec{S}_{i} $$(A5)
here, \(\lambda_{i}^{*}\) minimizes \(\phi (X_{i} + \lambda_{i}^{*} S_{i} )\), it is known as one-dimensional minimization. \(\lambda_{i}^{*}\) is known as optimum step length along the direction of search \(\vec{S}_{i}\) and the quadratic interpolation method [28] is used to evaluate the optimum step length.
-
(3)
Evaluate \(\nabla \phi_{i + 1}\), that indicates the gradient of \(\phi\) at \(\vec{X}_{i + 1}\).
At \(\vec{X}_{i + 1}\), the new direction of movement is obtained as
where
with
and
-
(4)
Once the new direction of movement \(\vec{S}_{i + 1}\) is evaluated, continue steps (2) through (4) until the function \(\phi\) is minimized at \(X = X_{i + 1}^{*}\).
-
(5)
Set a new value of r that is equal to 1/10 of its present value and generate a new function \(\phi\) with the new value of r. Taking the end point of step (4) as a new starting point and repeating the above steps \(\phi (\vec{X},r_{k} )\) is minimized. This is continued until the specified convergence condition is satisfied.
1.3 QIM
The optimum step length (\(\lambda_{i}^{*}\)) along the search direction \(\vec{S}_{i}\) from the present point \(\vec{X}_{i}\) is evaluated by the quadratic interpolation method. In this method, three values of step length (\(\lambda\)) are chosen in a specific manner. A quadratic equation h(\(\lambda\)) is fit between these three points as an approximation of the actual curve \(\phi (\lambda )\). The value of optimum step length along the search direction is obtained by differentiating h(\(\lambda\)) with respect to \(\lambda\) and its closed-form expression can be obtained in terms of the \(\phi\) function value at three chosen points. Major steps are given below.
The function \(\phi (\lambda )\) is approximated by a quadratic function h(\(\lambda\)) which has an easily determinable minimum point. h(\(\lambda\)) is expressed as:
the minimum of which occurs when
The constants a, b and c of the approximating quadratic can be determined by sampling the function at three different \(\lambda\) values, \(\lambda_{1}\), \(\lambda_{2}\) and \(\lambda_{3}\) and solving the equations:
where, \(\phi_{1}\) denotes \(\phi_{1} (\lambda_{1} )\) and so on.
The constants a, b and c can be determined as follows.
Further details of this method have been elaborated in standard textbooks on optimization techniques [28].
Rights and permissions
About this article
Cite this article
Hati, S., Panda, S.K. & Nainegali, L. Inverse analysis for parameter estimation of sandy soil with axially loaded pile using nonlinear programming. Sādhanā 47, 9 (2022). https://doi.org/10.1007/s12046-021-01773-3
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s12046-021-01773-3