1 Introduction

COVID-19 pandemic caused by SARS-CoV-2 (referred to as coronavirus hereafter), which had hit the world at the end of the year 2019, has generated an unprecedented health and economic crisis throughout the world. As the disease menaces the world, one of the important scientific questions is how the coronavirus spreads and transmits among humans. It is well-documented that the virus is transmitted from one human being to another via respiratory droplets [1,2,3,4]. To mitigate the virus transmission, it is important to understand the different routes of transmission and mechanisms pertaining to those routes [5]. The spread of infection may stem from aerosols formed by the respiratory droplets which are generated by a diseased person during coughing, sneezing, and moist speaking; wherein the persistence of the aerosols play a significant role in determining the risk of disease spread [6,7,8,9,10,11,12]. The guidelines for limiting the airborne disease transmission via airborne route have been demonstrated [13]. However, a conclusive evidence to support potential airborne disease transmission remains inconclusive [14]. Apart from the airborne route, the contaminated respiratory droplet may also get deposited on a surface to form fomite, which serves as a potential source of infection spread upon touch [15, 16]. Therefore, apart from the usage of face masks, face shields, social distancing [17,18,19,20,21,22,23,24,25], sanitization of frequently-touched surfaces was also recommended by the World Health Organization (WHO) [26]. It is noteworthy that, although the airborne route is thought to be the predominant route of transmission, the fomite route of transmission cannot be totally ruled out while assesing the total risk of infection spread, especially in a typical indoor environment [27]. In fact, previous study has shown that a higher percentage of exposed virion is realised on substrate precipitates of dried mucosalivary droplets than their airborne counterparts [28]. This fact marks the importance to understand the survival of coronavirus on different surfaces.

It was demonstrated earlier that the aqueous phase of the respiratory droplet serves as a medium for survival of an enveloped virus such as coronavirus. Since evaporation determines the ultimate fate of the droplet, it plays a paramount role in dictating the survival of the virus [29,30,31]. It has been demonstrated that the time decay of virion concentration is correlated to the volume loss of the respiratory droplet due to evaporation [32]. For this reason, the survival of virus and the associated risk of infection spread is significantly correlated to the environmental conditions such as ambient temperature and relative humidity [33, 34].

Based upon the above mentioned facts, it is imperative to study and understand evaporation and thereby survival of coronavirus under different environmental conditions. Furthermore, since the fomite route of transmission has the potential to boost the disease outbreak especially in public places, mitigating the infection spread demands a concrete understanding of virus survival on different surfaces. To this end, Bhardwaj and Agrawal [35, 36] investigated the evaporation of a respiratory droplet and a residual thin-liquid film after drying of the bulk droplet on different surfaces. Their formulation demonstrated that by considering a surrogate droplet of pure water, i.e., ignoring the presence of virus and the associated shear stress, and the effect of biological solutes contained in mucosalivary droplets; the drying time-scale of the droplet and the residual thin-film correlates with the survival timescale of coronavirus. Based upon the model predictions, they suggested a way of reducing the chance of COVID-19 infection by tailoring the surface wettability [37]. In particular, the evaporation of the bulk droplet is governed by the diffusion of the liquid-vapor outside the droplet; while the residual thin-film evaporation is governed by the disjoining pressure within the thin-film. This makes the evaporation of the thin-film much slower than that of the bulk droplet. While the bulk droplet vanishes within a few seconds after its deposition onto a surface, the thin-film lifetime is of the order of hours or days, which explains the survival of coronavirus for days on surfaces [36]. It was shown that the temporal decay of the thin-film thickness scales with the decay of virus titer reported earlier [38, 39]. Therefore, the thin-film lifetime contributes to the maximum portion of the virus survival time and attention should be devoted to look at the drying time scale of the residual thin-film.

In connection to the above, Chatterjee et al [40] recently studied how different is the drying mechanism of liquid thin-film on porous surfaces, e.g., cloth, paper; as compared to impermeable surfaces, e.g., glass, stainless steel and polypropylene. The process of thin-liquid film evaporation is much faster on porous surfaces than impermeable surfaces, which was attributed to an augmented excess energy (disjoining pressure) within the thin-film for the case of porous materials due to the presence of horizontally oriented fibers and void spaces on the surface. The study thereby explains the lesser survival of coronavirus on porous surfaces found earlier in titer measurements [38, 39].

The brief literature survey shows that the understating of thin-liquid film evaporation on a surface is important in deciding the coronavirus survival time on different surfaces. Therefore, the present review focuses on the scientific investigations on thin-liquid film drying mechanisms on different surfaces. The prior-art contributions by Bhardwaj and Agrawal [35, 36] and Chatterjee et al [40] have been taken in this review as the basis. Thus, the present review is useful to demonstrate the safety aspect of different materials under use and to possibly mitigate the disease spread via the fomite route.

The review is organized as follows. First, the hypothesis for understanding the coronavirus survival on different surfaces is reviewed in section 2. In section 3, the findings of analytical models depicting the coronavirus survival on impermeable and porous surfaces and comparison with previous virus titer measurements are reviewed. Subsequently, recent scientific investigations on designing antiviral surfaces by surface engineering are reviewed in section 4. Finally, conclusions and specific recommendations to suppress the disease spread are highlighted in section 5.

2 Hypothesis

A few hypotheses have been proposed in order to answer the question “Why does SARS-CoV-2 survive longer on plastic than on paper?” The hypothesis of Corpet [41] was based upon prior-art studies (cf. references 7-11 within reference [41]) on Influenza A virus. The brief literature review in [41] revealed that experiments on sedimentation of influenza virus with deuterated water showed that these viruses contain 60 \(\%\) water, and that water corresponds to 150-230 \(\%\) of the dry weight of these virus. Like influenza, coronavirus is also enveloped within a lipid membrane which is collected from the host-cell and thereby, it takes some amount of crytoplasm which causes it to contain approximately two third of water. Secondly, it was argued that the inactivation of enveloped viruses due to dehydration would occur by structural changes of the bilayer membrane, that would need water on both its sides to remain stable (cf. reference 8,9 within reference [41]). Drying would also lead to the oxidation of lipids and the occurrence of Maillard reaction of proteins. Furthermore, Kumar et al (cf. reference 11 within reference [41]) experimentally visualized that respiratory droplets from human breath are condensed on a solid surface, which subsequently dries and leaves behind more stable residues of “a few micrometers”. Corpet [41] postulated that the size of coronavirus virion is 10-100 time lesser than the aforesaid residue, and hence the residues could be large enough for viable virus survival. Based upon these observations, it was conjectured that the coronavirus would survive for longer duration on less wettable impermeable surface (e.g. plastic) than porous surfaces (e.g., paper). However, the discussion presented in [41] was purely hypothetical, derived from the knowledge gained from the studies on influenza viruses. The hypotheses did not have a direct link to the survival of SARS-CoV-2 on different surfaces. In addition, a detailed scientific investigation along with a mechanistic model depicting the coronavirus survival time-scales on different high-touch surfaces and a validation against the recently reported titer measurements [38, 39] were lacking. Hence, no conclusive investigations existed as to what are the key factors and governing mechanisms determining SARS-CoV-2 survival on different surfaces. Also how these factors and mechanisms are modulated for the case of porous surfaces as opposed to impermeable surfaces that make porous surfaces less favorable for virus survival remained unanswered.

From the discussion above, it is apparent that there was an urgent need to systematically analyse the drying of respiratory droplets and the residual thin-film on impermeable and porous surfaces to elucidate the corrlation between the aqueous-phase lifetime of a respiraotory droplet and the coronavirus survival time on different frequently-touched surfaces. Bhardwaj and Agrawal [35] made a valuable contribution in this direction by first analysing the drying of a respiratory droplet on different surfaces on the basis of the diffusion-limited evaporation model, wherein they reported a weak correlation between the drying-times under different atmospheric conditions and the infection growth rate under the same conditions. Based upon the knowledge gained, they suggested ways to mitigate the disease spread via the fomite route by tailoring the wettability of personal protection equipment [37].

However, the bulk of the respiratory droplet undergoes diffusion-limited evaporation [35] and takes a few seconds to dry out; while the coronavirus survives for hours/days on surfaces, as reported in published measurements [38, 39]. Hence, the question arose: How coronavirus survives for hours to days on surfaces? Bhardwaj and Agrawal [36] first answered this question by having attributed the long virus-survival time to a slower evaporation rate of a residual thin-film which is left on the underlying surface after the bulk respiratory droplet vanishes. They established a correlation between the time-variation of the aqueous-phase mass of the aforesaid residual thin-film and the temporal decay of SARS-CoV-2 titer reported in published measurements [38, 39]. Hence, the lifetime of the residual thin-film contributes to the maximum portion of coronavirus survival time on different surfaces. Thereafter, another question arose: How the evaporation mechanism of the residual thin-film is modified for the case of porous materials that makes them less favorable for coronavirus survival? Chatterjee et al [40] first answered this question by exploring how the solid-liquid interfacial energy is modified due to the typical geometric features of the porous surfaces leading to a faster evaporation of the residual thin-film on them as compared to that on impermeable surfaces. Their analysis corroborated well with the measured SARS-CoV-2 survival time-scale on porous surfaces such as cloth, paper [39]. The work by Chatterjee et al [40] was subsequently referenced in the “Science Brief” report of the US Centers for Disease Control and Prevention (CDC) on April 05, 2021 [27] to demonstrate the shorter survival of coronavirus on porous surfaces as compared to impermeable surfaces. Inspired by their findings [40], Chatterjee et al [42] further analysed the drying of residual thin-film on physically textured surfaces with varied wettability. They demonstrated how the intrinsic wettability and texture can be optimized to obtain a minimal virus survival time on impermeable surfaces; thereby disclosing a design of antiviral surfaces to suppress the spread of COVID-19. The interesting findings of references [36, 40, 42] are the subject of the present review and will be presented in the following sections.

3 Thin-liquid film evaporation in connection to coronavirus survival on different surfaces [36, 40]

Figure 1
figure 1

Reprinted from references [36, 40] with permission from the American Institute of Physics, copyright: 2021.

Schematic of the problem (a) deposition of respiratory droplet on a smooth surface and subsequent thin-film formation and (b) deposition of respiratory droplet on a porous surface and subsequent thin-film formation.

Full size image

In this section, we review the prior-art contributions by Bhardwaj and Agrawal [36] and Chatterjee et al [40], wherein they analysed the drying of thin-liquid film which remains after the evaporation of the bulk respiratory droplet. A schematic of the problem considered by the authors [36, 40] is shown in figure 1. It was demonstrated that when a respiratory droplet is deposited on a smooth solid surface, it first undergoes diffusion-limited evaporation, by virtue of which, the bulk droplet mass vanishes. Thereafter, a thin-residual liquid-film is left on the solid surface, which has a pancake-like shape. The final fate of the surviving virus depends on the lifetime of this residual thin-film. Figure 1(b) depicts the scenario for a porous surface [40]. For the bulk droplet, in addition to the diffusion-limited evaporation, capillary imbibition through the pores also contributes to its mass loss. The capillary imbibition is a much faster process than the diffusion-limited evaporation. After the bulk droplet is vanished, a thin-residual film is left on the exposed parts of the porous surface. The formation of the thin-film and its lifetime is quite different on impermeable and porous surfaces, which was deciphered earlier [40] and is the subject of review in the present section.

3.1 Thin-film evaporation and coronavirus survival on smooth, impermeable surfaces

Figure 2
figure 2

Reprinted from reference [36] with permission from the American Institute of Physics, copyright: 2021.

Temporal variation of thin-film thickness with time for (a) glass (b) polypropylene, and (c) stainless steel and comparison with previous titer measurements. On the left axes, the time varying film thickness, h(t) are plotted. On the left axes the data for previous virus titer measurements [39] is reproduced for comparison. The detection limit for the titer measurements has also been indicated in the figures.

Full size image

Bhardwaj and Agrawal [36] analysed the drying of the residual thin-film on smooth, impermeable surfaces, namely glass, polypropylene, and stainless steel, and examined the variation of film-thickness, h(t), with time t. They examined that the temporal decay of thin-film mass, or h(t), correlates with the temporal decay of coronavirus titer with time recorded in earlier experiments [39]. It was demonstrated that when the bulk droplet is vanished, the diffusion-limited evaporation ceases to drive the mass-loss of the liquid content, and the evaporation of the residual thin-film is governed by the disjoining pressure or the excess energy within the thin-film [43, 44]. Thereby, the evaporation rate of the thin-film is much lesser, which is the cause of long survival of coronavirus on different surfaces. Based upon the above-mentioned, physical considerations, they derived a simplified governing equation for the thin-film mass loss (cf. eq. (11) in reference [36]). While Bhardwaj and Agrawal [36] adapted an iterative approach to obtain variation of h(t) with t, Chatterjee et al [40] obtained an exact solution for the same (cf. eq (8) in reference [40]). Further a method for obtaining the Hamaker constant associated with the disjoining-pressure was formulated very recently [42].

In this section, while we review the results reported by Bhardwaj and Agrawal [36], the h(t) vs. t curves for the substrates under consideration (glass, polypropylene and stainless steel), shown in figure 2, have been obtained by using the exact solution given by Chatterjee et al [40, 42]. Figure 2 shows the results for glass, polypropylene (plastic) and stainless steel respectively. The titer values measured in an earlier study [39] are reproduced in the same plots for comparison. It can be seen that the temporal variation of thin-film thickness agrees qualitatively well with the time-variation of virus titer. The slope between two matches with reasonable fidelity. Now the focus is on the comparison between the virus survival time and the thin-film lifetime. On glass, the virus survival time was found to be \(\sim \)4 days, i.e., 96 hours. The present analysis returns a thin-film lifetime of \(\sim \) 104 hours. Similarly, the virus survival time was found to be \(\sim \)7 days (168 hours) on both polypropylene and stainless steel. The present model returns a thin-film lifetimes of \(\sim \) 96 hours and \(\sim \) 24 hours respectively. Therefore, the model could capture the reason behind the long-survival of coronavirus on different surfaces.

Chatterjee et al [40] noted that since the disjoining-pressure essentially stems from the intermolecular interaction between the liquid-vapor and the solid-liquid interfaces of the thin-film, it is the representative of the wettability of the underlying surface. Hence, the evaporation rate of the liquid thin film would be slower on less-wettable surfaces as they have lower surface free energy (higher contact angle). Reference [40] reports that the contact angles of water on glass, plastic and stainless steel are \(\sim \) 39\(^{\circ }\), 86\(^{\circ }\), and 90\(^{\circ }\) respectively. From these observations, it was concluded that the surface energy decreases progressively from glass to stainless steel. Consistent with the above argument, the film evaporation rate [36] (cf. figure 2) as well as the survival-time of the coronavirus observed in the titer measurements [39] increases progressively from glass to stainless steel. The role surface wettability in dictating its susceptibility to virus survival was thus deciphered.

3.2 Thin-film evaporation and coronavirus survival on porous surfaces

Chatterjee et al [40] deciphered that the much shorter survival of coronavirus on porous surfaces [39] can be attributed to an enhanced thin film evaporation rate. The essential physics demonstrated by the authors is reviewed in this subsection.

Figure 3
figure 3

Reprinted from reference [40] with permission from the American Institute of Physics, copyright: 2021.

Droplet interaction with porous media recorded by high-speed visualization. (a) Paper, side view (b) Paper, top view (c) Cloth, top view. The side views show the temporal variation of the droplet geometry and the top views record the droplet spreading; formation and persistence of the wetted patch at different times (indicated by the red dotted circles) (d(i)) Temporal variation of contact angle on paper and cloth derived from the side views (cf. (a)). The contact angle exhibits an exponential decay due to droplet spreading and imbibition through the pores. (d(ii)) From the top views (cf. (b), (c)): temporal variation of wetted diameter on paper and cloth as the droplet spreads on the surface.

Full size image
Figure 4
figure 4

Reprinted from reference [40] with permission from the American Institute of Physics, copyright: 2021.

(a) Time-variation of normalised droplet volume on glass and paper, and (b) Normalised drained droplet volume plotted as a function of square root of time for paper, and linear fitting showing the applicability of Washburn’s equation.

Full size image

Chatterjee et al [40] reported that when a droplet is deposited on a porous surface, it undergoes spreading due to the adhesive interaction between the liquid at the contact-line and the horizontally oriented fibers present on the porous surface and also experiences capillary imbibition through the pores. The combined effect of spreading and imbibition causes a rapid decay in the contact angle. The typical phenomena in shown in figure 3. The contact angle exhibits an exponential decay with time and the wetted radius increases continuously to an asymptotic value. The govering equation for the spreading and the associated fitting parameters are reported in reference [40]. It was also understood that the bulk droplet mass loss on porous surfaces is, in principle, governed by the Washburn’s equation [45], which states that the drained volume of the liquid, \(V_{d}\) varies as the square root of time t. This is opposed to the case of impermeable surface, wherein the diffusion-limited evaporation governs the mass-loss process [46,47,48]. To further strengthen this point of view, the temporal decay of normalised droplet-volume is reproduced herein from Chatterjee et al [40] as figure 4(a). It is seen that while the volume loss of the bulk-droplet exhibits a linear trend for the case of glass (an impermeable material), that for the case of paper (a porous material) exhibits a non-linear trend. It can also be observed that the bulk-droplet volume loss is much faster on porous surface, than that on impermeable surface. Similarly, figure 4(b) shows that the drained volume, \(V_{d}\), varies as \(\sqrt{t}\), and thereby, satisfying the Washburn’s equation [45]. We note that in reference [40], due to an inadvertent error, the x-axis scales of figure 4 were incorrect. The correct plots are given in figure 4 of the present article. The qualitative trends and the associated discussion however do not change in any way by the present corrections.

Based upon the above observation, Chatterjee et al [40] adapted an argument similar to that of Wenzel [49,50,51] to demonstrate that due to droplet spreading and the effective solid-liquid interfacial area modification by the presence of the void spaces, the disjoining-pressure within the thin-film is augmented for the case of porous surfaces, which leads to a faster evaporation of the thin-film. The modified governing equation of thin-liquid film evaporation on porous surfaces is depicted in eq. (15) of reference [40]. This way, the virus survival time-scale on porous surfaces is much lesser as compared to that on impermeable surfaces. Typical results found by Chatterjee et al [40] are reproduced in figure 5, for paper and cloth.

Figure 5
figure 5

Reprinted from reference [40] with permission from the American Institute of Physics, copyright: 2021.

Model predictions for temporal variation of thin-film thickness on (a) cloth and (b) glass.

Full size image

From figure 5, it is seen that the thin-film lifetime on cloth is \(\sim \)60 hours, which is in reasonable agreement with the virus survival timescale found from titer measurements [39] (\(\sim \)2 days or 48 hours). For paper, the model predicted a thin-film lifetime of \(\sim \)5 hours, while the titer measurements [39] revealed a coronavirus survival time-scale of \(\sim \)3 hours on paper. Chatterjee et al [40] observed that while the thin-film lifetime found from their model matches with the virus survival timescale on cloth with reasonable accuracy, on paper the agreement between the two data set is reasonable to the extent of order of magnitude. They attributed this quantitative discrepancy for the case of paper to the specific geometry (cf. figure 1(b)) they considered in their calculations. The typical geometry considered was closer to that of woven cloths while the geometry for the paper is more irregular than that of cloth. Therefore, they argued that the thin-film lifetime found from their model is closest to the virus survival time for cloth, while for paper, it agrees to the extent of order of magnitude. Yet, the combined information gained from figures 5(a and b) demonstrated the essential physics behind the lesser survival of coronavirus on porous surfaces: it is the fiber-liquid adhesion induced droplet spreading and the solid area modification by the voids that leads to an augmented disjoining-pressure and thereby a faster thin-film evaporation rate which makes them safer, from a COVID-19 point of view.

4 Survival of coronavirus on engineered surfaces: towards designing antiviral surfaces

From the discussion presented in the preceding section, we have learnt that a geometric feature induced augmentation in the disjoining-pressure causes the residual thin-film to evaporate faster on porous surfaces than on impermeable surfaces, making the porous surfaces lesser susceptible to virus survival. However, in most of the daily uses, especially in hospitals and pathological laboratory equipment, one cannot avoid the use of impermeable surfaces. This fact marks the importance of fabricating antiviral surfaces. Such surfaces are said to exhibit virucidal properties, i.e., surface properties due to which they become less conducive to the survival of virus and the viral load deposited on such surfaces diminishes rapidly [52, 53]. For example, polymer surfaces rich with polycations were found to cause rapid viral disintegration [54, 55]. Further, Nanoparticle (NP)-based antiviral agents have attracted significant atention of the scientific community for their prominent virucidal effects. For example, TiO\(_2\) nanoparticles are well-known for their photocatalytic properties. TiO\(_2\)-NP induced photocatalytic reaction leads to the formation of reactive oxygen species which causes a disturbance to the phospholipid bi-layer and thereby oxidative damage of genetic information happens, resulting in viral disintegration [56]. In addition, it was demonstrated that Silver nanoparticles (AgNPs) can be incorporated into polysulfone membranes which exhibit strong antibacterial and antiviral effects [57]. The reason behind their antiviral effects was not properly understood, however, it was envisioned that the observed antiviral effects were probably due to a change in the membrane permeability, depth of filtration, electrostatic adsorption, or inactivation by Ag\(^+\) ions [52]. On the other hand, solid and mesoporous silica particles fucntionalized with glycosaminoglycan were implemented to attract viral glycoproteins and eliminate virus entry to host cells in solution. The observed effects were attributed to the electrostatic and hydrophobic interaction between the glycosaminoglycan coated nanoparticles and the virus (HSV-1 and 2) [58]. However, such coating technologies suffer from lack of durability and have limited mechanical stability, and thereby, design and fabrication of more robust antiviral surfaces are required [52, 53, 59].

Figure 6
figure 6

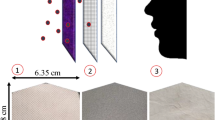
Reprinted from reference [60] with permission from the American Chemical Society, copyright: 2021.

SEM images of nanostructured aluminum surfaces after wet-etching. Further permissions related to the material excerpted should be directed to the American Chemical Society.

Full size image
Figure 7
figure 7

Reprinted from reference [60] with permission from the American Chemical Society, copyright: 2021.

Virus titer measurements (TCID\(_{50}\)/mL in a log\(_{10}\) scale) on pristine and engineered aluminum surfaces. Further permissions related to the material excerpted should be directed to the American Chemical Society.

Full size image

To the best of our knowledge, Hasan et al [60] made a valuable contribution in this direction by fabricating antiviral surfaces. In their study, they fabricated nanostructured aluminum surfaces by wet-etching technique. The wet-etching technique created a surface on which randomly oriented nanostructures grouped in ridges were formed (cf. figure 6). The process also led to the formation of Aluminum hydroxide. A reduction in the contact angle from 96.3\(^\circ \) to 17.7\(^\circ \) and roughness of area percent \(\sim \)23.8 were recorded for prolonged etching. The engineered surfaces by wet-etching process exhibited prominent virucidal properties. The results from reference [60] have been reproduced herein in figure 7. Strikingly, while the SARS-CoV-2 virus remained viable on pristine aluminum surfaces for more than 24 hours, on the engineered aluminum surfaces, it was effectively inactivated within 6 hours. Thereby, the contribution by Hasan et al [60] is a valuable one to obtain antiviral surfaces, from a safety point of view.

Inspired by the work by Hasan et al [60] and the knowledge gained from reference [40] (cf. section 3.2), Chatterjee et al [42] recently reported design of antiviral surfaces with varied wettability and texture, by analysing drying of a residual thin-film left behind an evaporated respiratory droplet on engineered surfaces. They demonstrated that there exists an optimum range of wettability and texture, in which the most prominent antiviral effects can be achieved. In brief, Chatterjee et al [42] showed that a surface engineering process should include a chemical treatment to convert an intrinsically hydrophobic surface to a hydrophilic one, and thereafter physical texturing is required to achieve an optimum virucidal effect. They considered two kinds of engineered surfaces (cf. figure 8): (i) surfaces with rectangular parallel grooves (cf. figure 8(a)) and surfaces with rectangular pillars (cf. figure 8(b)); as it was previously demonstrated that surfaces with arbitrary geometry can be well-approximated with a square-wave pattern in two-dimensions [61]. A combined effect of intrinsic wettability, i.e., surface energy and roughness on the antiviral effects was demonstrated [42]. Figures 8(c and d) depict the thin-film lifetime in the context of coronavirus survival time on both the engineered surfaces considered by Chatterjee et al [42]. The surface energy was represented in terms of an intrinsic contact angle, \(\theta _i\); and the roughness was represented in terms of the roughness factor, r, which is defined as the ratio between the actual area of a rough surface and its projected area. Based upon the developed model, which was subsequently validated with the measurements of Hasan et al [60], Chatterjee et al [42] deciphered that surfaces with lower surface energies are more susceptible to the coronavirus survival. Hence, an antiviral surface engineering process should include a chemical treatment by which the surface in question should be first made hydrophilic (\(\theta _i<90^{\circ }\)), and thereafter, physical texture be induced to further impart antiviral properties. The residual thin-film lifetimes in the context of coronavirus survival times on the engineered surfaces were evaluated based upon the well-known Weznel and Wet-Cassie arguments [49]. As shown in figures 8(c and d), irrespective of the nature of the surface geometry, there exists an optimum in the residual thin-lifetime \(t_f\) with respect to \(\theta _i\) and r: the thin-films in the regions of \(r\sim 5-11\), and \(\theta _i\sim 20^{\circ }-70^{\circ }\) dry at the earliest (\(t_f\sim 5-8\) hours). Based upon the findings, Chatterjee et al [42] presented a case-study of the virucidal properties of the designed antiviral surfaces across a varied wettability and texture (cf. figure 9). For a given surface, if \(\theta _{0}>90^{\circ }\), the surface engineering process should include a chemical modification by which \(\theta _{i} < 90^{\circ }\) is obtained in order to enhance the thin-film evaporation rate and thereby the virucidal effects by introducing additional roughness. Furthermore, surfaces with taller and closely packed surface heights (say, for example \(a/h\sim 0.1\) and \(a/g\sim 0.9\)) fall within the the aforementioned range required for optimization with respect to roughness (\(r\sim 10\)), and therefore returns the least thin-film lifetime (\(t_f\sim 6\) hours) if \(\theta _{i}<90^{\circ }\) falls within the aforementioned range required for optimization with respect to intrinsic wettability (say, for example, \(\theta _i=60^{\circ }\)). At lower roughness (\(r\sim 1-3\)), the thin-film lifetime of the engineered surfaces can be minimized by lowering \(\theta _{i}\) (say, for example \(20^{\circ }\)). The thin-film lifetime in this limit approaches to that of smooth surfaces having higher wettability (\(\theta _{0}\sim 20^{\circ }\)). This way, this study is useful to fabricate antiviral surfaces and thereby is helpful to mitigate the disease spread via fomite route from hospitals, pathological laboratories.

Figure 8
figure 8

Reprinted from reference [42] with permission from the American Institute of Physics, copyright: 2021.

(a) Schematic of an engineered surface with rectangular parallel grooves (b) Schematic of an engineered surface with rectangular pillars. In (a) and (b), h: surface height with respect to the base, a: lateral dimension of the heights, g: gap between the heights and \(q=a+g\): pitch. (c) Residual thin-film lifetime in the context of coronavirus survival time with varying intrinsic wetttability (contact angle, \(\theta _i\)) and roughness factor (r) on surfaces decorated with rectangular parallel grooves, (d) Residual thin-film lifetime in the context of coronavirus survival time with varying intrinsic wetttability (contact angle, \(\theta _i\)) and roughness factor (r) on surfaces decorated with rectangular pillars.

Full size image
Figure 9
figure 9

Reprinted from reference [42] with permission from the American Institute of Physics, copyright: 2021.

A case-study depicting the antiviral properties of engineered surfaces across varied wettability and physical texture.

Full size image

Next, we discuss the applicability of the findings reviewed herein. The knowledge gained from this review can be expanded to assess the risk of transmission of other respiratory disease such as Influenza A, including the other sub-classes of the coronavirus family. This is realized by identifying the role of evaporation/aqueous phase mass loss in the survival of enveloped viruses, as discussed in the introduction section and in section 2. Buckland and Tyrrell [29] experimentally investigated the loss of infectivity of 19 different types of viruses upon drying. Similar concept was disclosed later [30] wherein, it was particularly demonstrated that porosity is learnt to be a major governing factor in determining the inactivation rates of influenza type viruses. Furthermore, Doremalen et al [38] experimentally investigated the virus titer of two sub-classes of coronavirus family: SARS-CoV-1 and SARS-CoV-2 in aerosols and different surfaces. They reported that both the sub-classes follow similar stability kinetics in aerosols and on impermeable and porous surfaces. Therefore, a quick literature review reveals that for all such viruses (influenza, SARS-CoV-1, SARS-CoV-2) porous materials are particularly unfavorable for virus survival. Hence, although the studies reviewed herein [36, 40, 42] analysed the drying of respiratory droplets and a residual thin-film to compare the survival time-scales of SARS-CoV-2, the knowledge can readily be extended to decipher the survival of respiratory disease causing viruses such as Influenza, and the other sub-classes of the coronavirus family.

Further, we comment on the relative importance of the fomite route of transmission as compared to the airborne route in the context of SARS-CoV-2, which is a contemporary topic of debate. Some researchers opine that the airborne route is the main vector in the disease transmission, and ignore the role played by the fomite route [62]. The argument is based upon the fact that detection of viral RNA on high-touch surface does not necessarily reflect the infectivity of the virus. Furthermore, experiments that measured infectious virus titer on frequently used surfaces [38, 39], were performed in a controlled environment and thereby, may not reflect real-world situations. For example, the initial viral load that was in the viral inoculum for experimentation [39] may not be consistent with that present in a real respiratory droplet. Further, laboratory experiments optimize the recovery of virus from the inoculated surfaces by use of viral transport media which does not necessarily reflect the potential to pick up the virus from casual contact [39, 62]. Despite these facts, it should be noted that the previous virus titer measurements [38, 39] indeed had proven the potential of virus to infect cells (e.g., Vero E6 cells in [39]) after having recovered from different inoculated surfaces at the desired time points. A number of COVID-19 transmission cases, including the outbreak in April 2021 at Guangzhou, China; provided evidence to support that the fomite route is one of the possible modes of disease transmission [63, 64]. Indeed, the epidemiological data depicting the modes of COVID-19 transmission is “messy”, and hence the possibility of disease transmission through contaminated surfaces cannot be ruled out completely to asses the total risk of disease spread [62]. The potential of virus transmission by fomite route is also evident from the classical Wells evaporation-settling curve [65] owing to which nearly all respiratory disease (e.g., Influenza, norovirus) have the potential to spread infection through contaminated surfaces [29, 30]. Because of these reasons, the World Health Organization (WHO) and the US Centers for Disease Control and Prevention (CDC) still recommend frequent hand hygiene and avoid touching mouth, nose, and eyes with unwashed hands to mitigate the disease spread [27, 66]. The possibility of catching infection through fomite route is particularly prominent in typical settings such as hospitals, public gathering/waiting halls with poor ventilations [62]. Therefore, an understanding the virus survival time of different high-touch surfaces is important. Especially, the lesser virus survival time on porous surfaces and the design of antiviral surfaces, is an useful information to mitigate the disease spread via the fomite route. This marks the importance of the present review.

5 Conclusions and recommendations

In this paper, we have reviewed the recent scientific investigations on survival of coronavirus on impermeable and porous surfaces. Based upon the review the following knowledge is gained.

  1. (i)

    When a respiratory droplet from an infected subject is deposited on a surface, the surface becomes contaminated and thereby is vulnerable to disease spread. The respiratory droplet serves as a medium for the virus survival and therefore, evaporation dictates the overall survival time-scale.

  2. (ii)

    While the bulk of the respiratory droplet takes a few seconds to vanish by diffusion-limited evaporation, a much more stable thin-liquid film is left behind the respiratory droplet. The virus can still survive inside the thin-film, and the drying of the thin-film is much slower as it is governed by the disjoining-pressure within the film.

  3. (iii)

    The thin-film evaporation rate depends on the wettability of the underlying surface: the drying rate is lesser for lesser wettable surfaces making them significantly viable for virus survival.

  4. (iv)

    For porous surfaces, the thin-film evaporation is much faster which is triggered by an augmented disjoining-pressure due to fiber-droplet adhesive interaction induced droplet spreading and modification of effective solid-liquid interfacial area due to the presence of the void spaces. Thus, the porous materials are lesser conducive to virus survival.

  5. (v)

    One may tune the surface wettability and physical texture to impart optimized virucidal properties on impermeable surfaces.

For a better contrast and clarity of the above-mentioned concluding points, a summary of SARS-CoV-2 survival times on different surfaces of daily use and the correlation with residual thin-film lifetimes are depicted in table 1.

Table 1 SARS-CoV-2 survival time-scales on different surfaces of daily use and the correlation with residual thin-film lifetimes.
Full size table

Based upon the above conclusions, we make a few recommendations, which we have also highlighted in our earlier study [40]. Since cardboard boxes (a porous material) are commonly used by the e-commerce companies, they are deemed safer than boxes made of impermeable materials, say, plastic. Similarly, although the virus survival time is much less on paper, the time-scale of \(\sim \) 5 hours has to be kept in mind during exchange of notebooks and currency notes in a retail bank. This is a particularly relevant information to the policymakers regarding the reopening of schools. Similarly, the probability of disease spread from a cloth outlet is deemed to be lesser, as previously thought. We again emphasize that the present review focuses on the fomite route of transmission and the possibility of disease spread via airborne route has to be taken into account to asses the total risk of infection spread in the above-mentioned examples.