Skip to main content
SpringerLink
Log in

Aiding buoyancy driven flow and heat transfer features of converging and diverging trapezoidal cylinders

  • Published:
Sādhanā Aims and scope Submit manuscript

Abstract

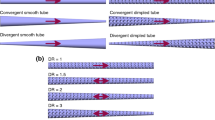
Numerical computations have been carried out to explore the influence of mixed convection heat transfer from heated trapezoidal geometries of two different configurations namely converging and diverging cylinders in a vertical domain. The recirculation length of the diverging cylinder is found to be more than that of the converging cylinder for all values of Re (5 to 40) considered in this study and this length decreases after introducing buoyancy effect. Drag coefficients decrease with increase in Re for a fixed Ri. However, drag increases for the increasing values of Ri (values considered up to 1). The drag coefficient is found to be the smaller for diverging cylinder than that of converging one. Local Nusselt number shows significant increase as Re and Ri values increase, which results in enhanced heat transfer. Keeping Ri fixed and increasing the value of Re results in the augmentation of heat transfer and is around 15% at Re = 5 and 23% at Re = 40 for Ri = 0 for a square cylinder with respect to diverging cylinder. Under the influence of aiding buoyancy, the values of average Nusselt number (\( \overline{Nu} \)) for the diverging cylinder are higher compared to that of converging cylinder. A correlation expressing functional relationship of \( \overline{Nu} \) with Re and Ri has also been generated.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Figure 1
Figure 2
Figure 3
Figure 4
Figure 5
Figure 6
Figure 7
Figure 8
Figure 9
Figure 10
Figure 11

Similar content being viewed by others

Abbreviations

B :

Front width of trapezium, m

C p :

Specific heat of fluid, J kg−1 K−1

CV:

Control volume

C D :

Overall drag coefficient \( \left( { = \frac{{2F_{D} }}{{\rho v_{\infty }^{2} B}} = C_{Dp} + C_{Dv} } \right) \)

C Dp :

Pressure drag coefficient \( \left( { = \frac{{2F_{Dp} }}{{\rho v_{\infty }^{2} B}}} \right) \)

C Dv :

Viscous drag coefficient \( \left( { = \frac{{2F_{Dv} }}{{\rho v_{\infty }^{2} B}}} \right) \)

F Dp :

Pressure drag force on the object, N m−1

F Dv :

Viscous drag force on the object, N m−1

F D :

Drag force on the object, N m−1

g :

Acceleration because of gravity, m s−2

Gr :

Grashof number \( \left( { = \frac{{g\beta \left( {T_{w} - T_{\infty } } \right)B^{3} }}{{v^{2} }}} \right) \)

h :

Local heat transfer coefficient, W m−2 K−1

\( \overline{h} \) :

average heat transfer coefficient, W m−2 K−1

H u :

Upstream distance, m

H d :

Downstream distance, m

H T :

Total height, m

k :

Coefficient of thermal conductivity, W m−1 K−1

Lr :

Wake length, m

L 1 :

Domain length, m

Nu L :

Nusselt number (local) \( ( = hB/k) \)

\( \overline{Nu} \) :

Average Nusselt number \( ( = \overline{h} B/k) \)

p :

Pressure, N m−2

P :

Pressure \( \left( { = \frac{p}{{\rho v_{\infty }^{2} }}} \right) \)

Pr :

Prandtl number \( \left( { = \frac{{\mu C_{p} }}{k}} \right) \)

Re:

Reynolds number \( \left( { = \frac{{\rho v_{\infty } B}}{\mu }} \right) \)

Ri :

Richardson number \( \left( { = \frac{Gr}{{\text{Re}^{2} }}} \right) \)

t :

Time, s

T :

Temperature, K

T w :

Constant wall temperature of solid surface, K

T ∞ :

Stream temperature, K

u :

Cross stream velocity, m s−1

U :

Cross-stream velocity (= u/v∞) (non-dimensional)

v :

Stream-wise velocity, m s−1

v ∞ :

Inlet free-stream velocity, m s−1

V :

Stream-wise velocity (= v/v∞) (non-dimensional)

x :

Cross stream coordinate, m

X :

Cross stream coordinate (= x/B) (non-dimensional)

y :

Stream-wise coordinate, m

Y :

Stream-wise coordinate (= y/B) (non-dimensional)

β :

Coefficient of volumetric thermal expansion, K−1

δ :

Size of the CV clustered around the object

θ :

Dimensionless temperature \( \left( { = \frac{{T - T_{\infty } }}{{T_{w} - T_{\infty } }}} \right) \)

μ :

Dynamic viscosity of the fluid, kg m−1 s−1

ρ :

Density of the fluid, kg m−3

τ :

Time (= t/(B/ v∞)) (non-dimensional)

References

  1. Badr H M 1984 Laminar combined convection from a horizontal cylinder - parallel and counter flow regimes. Int. J. Heat Mass Transf. 27: 15–27

    Article  MATH  Google Scholar 

  2. Ho C J, Wu M S and Jou J B 1990 Analysis of buoyancy-aided convection heat transfer from a horizontal cylinder in a vertical duct at low Reynolds number. Wärme und Stoffübertragung 25: 337–343

    Article  Google Scholar 

  3. Badr H M 1983 A theoretical study of laminar mixed convection from a horizontal cylinder in a cross stream. Int. J. Heat Mass Transf. 26: 639–653

    Article  MATH  Google Scholar 

  4. Sharma A and Eswaran V 2004 Effect of aiding and opposing buoyancy on the heat and fluid flow across a square cylinder at Re = 100. Numer. Heat Transf. A 45: 601–624

    Article  Google Scholar 

  5. Singh S, Biswas G and Mukhopadhyay A 1998 Effect of thermal buoyancy on the flow through a vertical channel with a built-in circular cylinder. Numer. Heat Transf. A 34: 769–789

    Article  Google Scholar 

  6. Singh S K, Panigrahi P K and Muralidhar K 2007 Effect of buoyancy on the wakes of circular and square cylinders: a Schlieren-interferrometric study. Exp. Fluids 43: 101–123

    Article  Google Scholar 

  7. Maudou L, Choueiri G H and Tavoularis S 2013 An experimental study of mixed convection in vertical, open-ended, concentric and eccentric annular channels. J. Heat Transf. 135: 072502–072509

    Article  Google Scholar 

  8. Venugopal A, Agrawal A and Prabhu S V 2010 Influence of blockage and upstream disturbances on the performance of a vortex flow meter with a trapezoidal bluff body. Measurement 43: 603–616

    Article  Google Scholar 

  9. Sharma N, Dhiman A K and Kumar S 2012 Mixed convection flow and heat transfer across a square cylinder under the influence of aiding buoyancy at low Reynolds numbers. Int. J. Heat Mass Transf. 55: 2601–2614

    Article  Google Scholar 

  10. Srinivas A T, Bharti R P and Chhabra R P 2009 Mixed convection heat transfer from a cylinder in power-law fluids: effect of aiding buoyancy. Ind. Eng. Chem. Res. 48: 9735–9754

    Article  Google Scholar 

  11. Lee T S 1998 Early stages of an impulsively started unsteady laminar flow past tapered trapezoidal cylinders. Int. J. Numer. Meth. Fluids 26: 1181–1203

    Article  MATH  Google Scholar 

  12. Sun Z 2011 Design and performance of the converging-diverging vortex flow meter. Metrol. Measur. Syst. 18: 129–136

    Google Scholar 

  13. Chung Y J and Kang S H 2000 Laminar vortex shedding from a trapezoidal cylinder with different height ratios. Phys. Fluids 12: 1251–1254

    Article  MATH  Google Scholar 

  14. Verma V K and Dhiman A 2017 A comparative study on cross-buoyancy mixed convection around expanded and tapered trapezoidal bluff bodies. Proc. Inst. Mech. Engineers, Part E: J. Process Mech. Eng. 231: 513–532

    Article  Google Scholar 

  15. Parveez M, Dhiman A K and Rasool T 2015 Transition to periodic unsteady and effects of Prandtl and Richardson numbers on the flow across a confined heated trapezoidal prism. J. Braz. Soc. Mech. Sci. Eng. 37: 1291–1307

    Article  Google Scholar 

  16. Kahawita R and Wang P 2002 Numerical simulation of the wake flow behind trapezoidal bluff bodies. Comp. Fluids 31: 99–112

    Article  MATH  Google Scholar 

  17. Dhiman A K and Hasan M 2013 Flow and heat transfer over a trapezoidal cylinder: steady and unsteady regimes. Asia Pacific J. Chem. Eng. 8: 433–446

    Article  Google Scholar 

  18. Dhiman A K and Ghosh R 2013 Computer simulation of momentum and heat transfer across an expanded trapezoidal bluff body. Int. J. Heat Mass Transf. 59: 338–352

    Article  Google Scholar 

  19. ANSYS User Manual, Ansys, Inc., Canonsburg, PA, 2009

    Google Scholar 

  20. Dhiman A K, Anjaiah N, Chhabra R P and Eswaran V 2007 Mixed convection from a heated square cylinder to Newtonian and power-law fluids. J. Fluids Eng. 129: 506–513

    Article  Google Scholar 

  21. Anjaiah N, Dhiman A K and Chhabra R P 2006 Mixed convection heat transfer from a square cylinder to power-law fluids in cross flow. In: ASME 2nd Joint U.S.-European Fluids Eng. Summer Meeting, Miami, FL

  22. Dhiman A K, Sharma N and Kumar S 2012 Wall effects on the cross-buoyancy around a square cylinder in the steady regime. Braz. J. Chem. Eng. 29: 253–264

    Article  Google Scholar 

Download references

Acknowledgement

The authors would like to thank the editors and the reviewers for their valuable and helpful suggestions that have enriched the quality of the article.

Author information

Authors and Affiliations

  1. Department of Chemical Engineering, National Institute of Technology Srinagar, Hazratbal, 190 006, India

    Malik Parveez

  2. Department of Chemical Engineering, Indian Institute of Technology Roorkee, Roorkee, 247 667, India

    Amit Dhiman

  3. Department of Mechanical Engineering, National Institute of Technology Srinagar, Hazratbal, 190 006, India

    G A Harmain

Authors
  1. Malik Parveez
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Amit Dhiman
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. G A Harmain
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Amit Dhiman.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Parveez, M., Dhiman, A. & Harmain, G.A. Aiding buoyancy driven flow and heat transfer features of converging and diverging trapezoidal cylinders. Sādhanā 43, 118 (2018). https://doi.org/10.1007/s12046-018-0862-6

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s12046-018-0862-6

Keywords

Search

Navigation