Introduction

The thermal performance of heat exchangers depends on their design efficiency and operating conditions. Entropy generation analysis and heat transfer augmentation techniques assist in optimizing the setting of geometrical and fluid flow parameters of heat exchangers, thus achieving the target operational energy efficiency. The research on heat transfer enhancement and entropy generation minimization for tube heat exchangers is continuously developed, and several advancements are achieved against the reference case of standard smooth pipes [1,2,3]. The use of dimpled or corrugated tubes, wavy surfaces, convergent tubes, flow turbulator inserts, swirl generators, and/or the use of nanofluids with high thermal conductivity are the most utilized heat transfer enhancement methods. These types of heat exchangers could cover many applications, including shell-and-tube, tubular, solar thermal receiver designs, etc. [4,5,6].

On an experimental basis, Chen et al. [7] investigated the thermal performance improvement of coaxial tubes with dimples at Re values in the range of 7500–52,000 for the flow of water. Their study investigated six dimple configurations, which all resulted in enhanced heat transfer rates with respect to the smooth pipe. Heat transfer ranges improved by 25–137% at fixed pumping power, and Re improved by 15–84% with a limited effect of friction. Kock and Herwig [8] calculated entropy production as a parameter for evaluating heat transfer efficiency in turbulent shear-dominant streams using CFD analysis. Four distinct entropy production mechanisms were mathematically formulated: heat flow caused by average and oscillating temperature domains and dissipation in average and oscillating velocity domains. They illustrated their experimental results by introducing an example of the local rate of entropy generation calculations for a pipe flow under heating conditions with a warped tape insert. Pressure drops and increased heat transfer rates were observed with the increased angle of the warped tape. The entropy generation analysis indicated that there is a unique optimal value for a particular angle of the warped tape. A combination of two heat transfer improvement methods for tube heat exchangers was introduced by Thianpong et al. [9]. In their experimental study, a twisted-tape swirl generator was applied to airflow inside a tube with dimples. Inside the enhanced tube, fully developed flow streams with Re ranging from 12,000 to 44,000 were tested, and the effects of twist ratio and pitch on the mean coefficient of heat transfer and the pressure drop were determined. The results showed higher values of the frictional losses and the coefficient of heat transfer inside the enhanced tube in reference to the same values for smooth and dimpled tubes separately. Wang et al. [10] studied experimentally the thermo-hydraulic performance of a tube with an ellipsoidal dimple geometry and with air as a working fluid. The heat and friction performance parameters for the elliptical tube with dimples were studied in reference to those for tubes with spherical dimples as well as those for smooth tubes. The results showed an increase in Nusselt number (Nu) for elliptically dimpled and spherically dimpled tubes by 38.6–175.1% and 34.1–158%, respectively, as compared to smooth tubes. However, the friction coefficient (f) was increased by 26.9 to 75% and 32.9 to 92% for tubes with elliptical and spherical dimples, respectively. Acceleration toward critical Re transition by around 1000 was achieved by the application of elliptical dimple roughness. The effect of artificial roughness geometry on increasing the heat transfer rate was explored by García et al. [11]. Three enhancement techniques were investigated: ribbed tubes, tubes with dimples, and helical wires on the basis of artificial roughness. The experimental findings revealed that the roughness configuration has a larger impact on the pressure drop attributes than on the thermal enhancement. For Re < 200, plain tubes were suggested; for 200 < Re < 2000, tubes with wire coils were advantageous, while for Re > 2000, corrugated and dimpled tubes were preferred for the lower pressure drop associated. Mwesigye et al. [12] numerically investigated minimum total entropy generation in a thermal absorber of a solar concentrator under inhomogeneous heat flux environments. Ray tracing and CFD techniques were used in their analysis. Flow with Re in the range of 1.0 × 104 to 1.36 × 106 and a range of 350—650 K for the working fluid was simulated inside the receiver tube. Their results revealed an optimum point with a minimum total entropy generation at any given combination of geometrical and flow parameters. Huang et al. [13] tried to increase the heat transfer of fully developed turbulent flows in a thermal absorber tube of a solar concentrating collector, on a numerical basis, by comparing three different geometrical configurations: dimples, helical fins, and protrusions. The results revealed that dimpled thermal receiver tubes have better thermal performance as compared to those with protuberances or spiral fins. Their research also investigated the effects of dimple size and orientation on thermal behavior. An optimization of the geometrical configuration of dimpled tubes for enhancing their thermo-hydraulic performance was introduced by Li et al. [14]. The steady single-phase flow of water inside enhanced dimpled tubes was numerically simulated, and it was observed that inline dimple orientation had improved heat transfer performance compared to staggered orientation. In addition, all dimple geometrical parameters except for dimple diameter were found to have a remarkable influence on heat transfer characteristics. Hong et al. [15] experimentally studied the hydrothermal attributes of turbulent airflow inside a plain tube equipped with twisted-tape inserts under uniform heat flux conditions for the heat transfer tests and isothermal situations for the pressure drop tests. The effects of different tape numbers and twisted ratios for a Re range of 580–19,200 were investigated. The results revealed an increase in Nu and f as the tape number increases and as the twisted ratio decreases. Additionally, it was shown that the intensity of viscous entropy creation increased as thermal entropy formation decreased. In the work of Sayed Ahmed et al. [16], tubes with internally repeated rips of different geometries were adopted. The study focused on heat transfer enhancement, entropy, and exergy analysis. Air flows with a Re range of 3.6 × 103–1.65 × 104 were utilized. The best thermo-hydraulic efficiency of the studied cases was focused on the performance evaluation criteria (PEC) of the flow. The best thermo-hydraulic efficiency, among others, was achieved with reduced entropy and increased exergy efficiency for ring-ribbed tubes. An experimental study of the condensation thermo-hydraulic performance of R-134a flow in tubes with dimples of varied depths was provided by Aroonrat et al. [17]. For all test runs on three dimpled tubes of various dimple penetrations and one plain tube, mass and heat flux ranges of 300–500 kg m−2 s−1 and 10–20 kW m−2, respectively, were adopted for all test runs on three dimpled tubes. Dimpled tubes revealed a considerable improvement in heat transfer but also showed larger pressure drops. Up to 83% of heat transfer intensification was accomplished in the tube with the largest dimple depth, in terms of efficiency index, in reference to the plain one. However, up to an 892% rise in pressure drop was also recorded for tubes with the largest dimple depth. The thermo-hydraulic and entropy generation performances of an enhanced thermal receiver tube of a parabolic trough solar collector were presented by Liu et al. [18]. Conical strips were inserted inside the thermal receiver to promote heat transfer. The impacts of the inner angle of the inserts, hollow diameter, and pitch ratio were investigated with varying Re from 5000 to 791,000, and fluid inlet temperature from 400 to 650 K. An increase of 45–203% in Nu and a reduction of 82.1% in heat loss were attained as a result of the proposed modification. However, the friction factor was increased by 6.17 to 17.44 times as compared to its value for the smooth thermal receiver. A range of 0.70–1.33 was obtained for the performance evaluation criteria (PEC), and an enhancement of 0.02–5.04% was achieved in the thermal efficiency of the receiver. The extreme decline in entropy production was found to be around 74%, and the highest increase in exergetic efficiency was around 6%. Ibrahim et al. [19] conducted a numerical study to investigate thermal performance improvement and entropy production analysis for tubes with conical-ring turbulators of different diameters and pitch ratios. The working fluid was air with Re in the range of 6000–25,000. Inserts of conical-ring shapes were utilized within three geometrical configurations: convergent, convergent–divergent, and divergent. Nu and f were intensified with the reduction in the diameter of the conical ring and pitch ratios. The Nu values obtained by using convergent, convergent–divergent, and divergent conical-ring configurations were found to be 330, 419, and 765 percent higher than those obtained by using the smooth pipe, respectively. Entropy production increased with increasing Re for all conical-ring configurations. In addition, the entropy production was found to be increased as the diameter ratio decreased. Dagdevir et al. [20] performed a numerical analysis of the thermo-fluid flow characteristics of water in an enhanced tube with trapezoidal dimples under fixed heat flux terms on the exterior of the tube. The analyses were performed with a Re range from 3000 to 8000 for various dimple diameters, trapezoid angles, and dimple pitch lengths. The results showed a maximum value of Nu that is larger by a factor of 2.1 than the plain tube for dimple diameter of 7 mm, trapezoid angles of 60°, and dimples pitch length of 10 at Re = 8000. In addition, the lowest f was obtained as 1.39 times larger than the plain tube for a diameter of dimple = 5 mm, trapezoid angles = 30°, and pitch length of dimples = 50 at the same Re. Lei et al. [21] introduced a parametric analysis for optimizing dimpled tube performance based on the response surface methodology (RSM) method. The dimple diameter, the penetration-to-diameter ratio, the distance along the centerline between two neighboring dimples-to-diameter ratios, and the number of dimples spanning a cross section were chosen as design criteria. Because one component influences the effect of an additional aspect on Nu and f, the results revealed that the interactions of the four geometric factors are large and intricate. Sun et al. [22] numerically explored the thermo-hydraulic attributes of turbulent flow within the tubes of a heat exchanger with various winglet vortex sources of rectangular geometries. The influences of geometric characteristics such as the number of winglets, height, and pitch ratios were experimentally investigated. Because of the greater mixing behavior induced by multi-directional vortices of higher turbulence, both f and Nu showed higher values with the increased number of winglets as well as the height ratio. Cheraghi et al. [23] presented a numerical investigation on tubes with deep dimples with the aim of heat transfer enhancement as compared to smooth tubes. The fluid flow pattern and the thermal performance indicators were studied for various dimple configurations (pitches, diameters, and depths) and Re = 500, 1000, and 2000. Dimpled tubes with higher depth and diameter as well as lower pitch showed higher rates of heat transfer (up to 600%) and also a considerable rise in the friction coefficient. In addition, by increasing the dimple diameter, pitch, and Re and decreasing dimple depth, the performance evaluation criteria (PEC) increased. Pandey et al. [24] presented a CFD study that used a Y-shaped insert to enhance the hydrothermal performance of a circular tube heat exchanger. The Re-Normalization Group k-\(\epsilon\) model was used for turbulence simulation in their study with variable perforation index as the geometrical parameter with Re ranging from 3000 to 21,000 and air as the heat transfer fluid. Higher perforation indexes resulted in higher f values due to turbulence induced in the core region, whereas lower perforation indexes resulted in lower f values and higher heat transmission. At Re = 3000, the maximum heat transfer rates were 5.05 times and 2.88 times for non-perforated insert cases over smooth tube. The thermo-hydraulic and entropy generation performance of laminar nanofluid flow inside a tube equipped with inserts of the helical screw type was investigated experimentally and numerically by Chaurasia and Sarviya [25]. The impact of single and double strips, as well as a variety of twist ratios, was studied. When compared to the plain tube, a tube with 1.5 twist ratio helical screw insert at Re = 300 resulted in a 421 percent increase in Nu values. At low twist ratios, the entropy production number was found to be reduced using double-strip inserts as compared to values obtained by using single-strip ones in the flow of nanofluid other than water. The best design of double-strip inserts for nanofluid flow was discovered. The mixed convection heat transport of a water–Al2O3 nanofluid between two cylinders was explored statistically by Shirazi et al. [26]. It was discovered that an increase in the volume percentage of the nanofluid causes an increase in the inner cylinder wall’s average Nusselt number. In a square chamber with a spinning blade at its center, Sepyani et al. [27] explored the mixed convection heat transport of a water–alumina nanofluid quantitatively. The findings revealed that while heat transmission increases most often with rising Rayleigh number, volumetric percentage of nanofluid, and blade length, it decreases with increasing Richardson number. The effect of utilizing tubes with dimples on the thermo-hydraulic performance of a concentrator type solar water heater was explored by Manoram et al. [28]. Within the collection tubes, simulations were conducted by altering the flow rate, number of dimples, and pitch-to-dimple diameter ratio. A maximum increase in Nu by a factor of 2.5 was reached at a flow rate of 2.5 kg min−3, as compared to the plain tube, by using six dimples per two pitches and a pitch-to-dimple diameter ratio of three. By comparing the value of the friction factor to that of a plain tube, a rise of 11.1 percent was recorded due to the presence of dimples. Hassan et al. [5] analyzed the thermo-hydraulic performance of turbulent flow inside a tube with conical rings using a numerical model. The results showed that solid diverging rings can attain greater Nu (up to 360.2 at Re of 26,000) while simultaneously having the largest f (5.04 at Re of 6000). Furthermore, while using solid diverging rings at Re of 6000, a factor of 1.1 (maximum) for the enhancement in thermal performance was obtained. Fadodun et al. [2] investigated the rate at which entropy is produced by turbulent flows inside tubes with various corrugation characteristics. The heat transfer fluid in their study was ferrosoferric oxide/water nanofluid. On viscous and thermal entropy production rates, the impacts of Re (in the range of 5.0 × 103 to 3.0 × 104) and nanoparticle intensity of 0.0–3.0% were investigated. The results showed that trapezoidal corrugated tubes are better in terms of thermal performance but with maximum friction factors, with a 2.92-fold increase in pressure drop and a 1.66-fold increase in average Nu for a 2.0 percent nanoparticle concentration at Re of 3.0 × 104. The production rates of normalized thermal and viscous entropy in circular, triangular, and trapezoidal corrugated pipes were estimated and compared. Khalil and Kaood numerically studied the influence of various configurations of double conical pipe heat exchanger on the thermal–hydraulic characteristics [29]. Flow mixing due to geometry as a technique for enhancing heat transfer characteristics was covered by Usefian et al. [30]. In their work, experimental and numerical analyses of a novel micromixer’s mixing performance were carried out. Recently, the thermo-hydraulic characteristics of dimpled conical tubes with various diameter ratios were investigated by Kaood et al. [31], aiming at highlighting the thermal design effectiveness of this new type of tube heat exchangers. The obtained results revealed that dimpled convergent tubes with 1.5 diameter ratios have the highest PEC values with about 30% improvement over the entire Re range, as compared to straight smooth tubes. Lastly, Kaood et al. [32] investigated the turbulent entropy production rate in straight/conical tubes with and without twisted-tape inserts. The results reveals that the presence of the twisted-tape inserts reduces the thermal entropy production rate nut increases the viscous entropy production rate.

Based on the extensive literature survey above, it can be inferred that geometrical modifications to the smooth heat transfer surfaces are promising in providing augmented heat transfer rates with acceptable pressure drop levels. Some proposals include tube surface corrugations or inserts of various geometries within tubes. The use of nanofluids with enhanced thermophysical properties is also being investigated in recent studies to contribute to more energy-efficient and compact designs of tube heat exchangers. In addition, tube heat exchangers with dimpled surfaces are good candidates for performance enhancement purposes since they offer an effective design-for-manufacturing criteria.

The present study introduces a comprehensive entropy generation analysis based on the thermo-hydraulic performance for new tube configurations with a dual effect of heat transfer enhancement (conical + dimpled), which adds value to the research development in this area by highlighting the designs with minimum entropy generation of this tube configurations. In addition, there is a need to shed light on research efforts that include flow inside conical tubes since the related literature is not rich with these kinds of studies [31, 33,34,35]. To the best of the authors’ knowledge, the proposed novel design and accompanying entropy generation analysis were not included yet in the specialized literature. The present study aims to numerically investigate flow patterns within dimpled conical tube configurations and to highlight the designs with minimum entropy generation. In addition, a comparative performance analysis is to be conducted in reference to smooth tubes of the same geometrical configurations and flow conditions, using different key performance indices. The study investigates variations of tube diameter ratio (1, 1.5, 2, 3, and 5) and Re (from 3000 to 40,000) to achieve the following objectives:

  • Understand the fluid flow and entropy generation patterns within the newly introduced tube geometries by studying the contours of thermal and viscous entropy generation quantities as well as dimensionless key performance parameters of entropy for various cases.

  • Analyze the performance of various entropy generation parameters: thermal entropy production rate (TEPR), viscous entropy production rate (VEPR), total entropy production rate, Be, Ns,en, and \({\phi }_{\rm s}\) under these conditions.

  • Provide a recommendation on the optimum tube design based on the best entropy generation performance.

Tube geometrical configurations

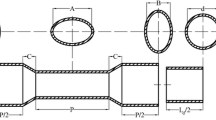
The geometrical configurations of the tube heat exchangers under consideration in this work are shown in Fig. 1. Various conical tubes with/without dimples with five different diameter ratios DR = 1, 1.5, 2, 3, and 5 are studied. The straight tube has an inner diameter (D) of 0.030 m and a length (L) of 0.5 m.

Fig. 1
figure 1

a Various geometrical configurations, straight and conical tubes with and without dimples. b Tubes with various DR with the flow direction

Full size image

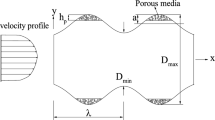
Figure 2a illustrates key geometrical parameters of the conical dimpled tube. Denoting D1 as the inner diameter at the tube entrance and D2 as the outer diameter at the tube outlet, the definition of the diameter ratio is \(\mathrm{DR}={D}_{1}/{D}_{2}\) for the convergent tube, while \(\mathrm{DR}={D}_{2}/{D}_{1}\) for the divergent tube. All considered diameter ratios are summarized in Table 1. Dimples were generated with a constant pitch P of 0.01665 m, a ratio of dimple-to-tube diameters (d/D) of 0.30, and a depth ratio (e/d) of 0.42. The number of circumferential dimples is eight along the tube length. These dimensions were selected based on their frequent utilization in related researches [8, 14, 15, 23].

Fig. 2
figure 2

a Detailed illustration of the conical dimpled tube geometrical parameters. b Boundary conditions of the mathematical model

Full size image
Table 1 Considered diameter and diameter ratios
Full size table

Governing equations and performance indicators

Thermo-hydraulic and entropy generation analysis

The flow field under investigation is 3D and incompressible, covering the whole turbulent range (Re = 3000–40,000) under steady-state conditions. The three main governing equations for solving the flow problem are the continuity, momentum, and energy equations, as follows [29, 30]:

The conservation of mass equation (continuity):

$$\frac{\partial ({v}_{\mathrm{i}})}{\partial {x}_{\mathrm{i}}}=0$$
(1)

where vi is the ith-direction of the local flow velocity.

The conservation of momentum equation:

$$\frac{\partial \left(\rho {v}_{\mathrm{i}}{v}_{\rm j}\right)}{\partial {x}_{\rm j}}=-\frac{\partial P}{\partial {x}_{\rm i}}+\mu \frac{\partial }{\partial {x}_{\rm j}}\left[\frac{\partial {v}_{\rm i}}{\partial {x}_{\rm j}}+\frac{\partial {v}_{\rm j}}{\partial {x}_{\rm i}}-\frac{2}{3}{\delta }_{\rm ij}\frac{\partial {v}_{\rm i}}{\partial {x}_{\rm j}}\right]+\frac{\partial }{\partial {x}_{\rm j}}\left(-\rho \overline{{{v}_{\rm i}}{{v}_{\rm j}}} \right)$$
(2)

Here, \({v}_{\rm j}\) is the jth-direction of the fluid velocity, and P is the local fluid pressure. The term \({v}^{\prime}_{\rm j}\) represents the fluctuated velocity, and the term \({\delta }_{\rm ij}\) represents the Kronecker delta, having a value of 1.0 if i = j or 0.0 if i ≠ j. The Reynolds stresses (\(-\rho \overline{{{v}_{\rm i}}{{v}_{\rm j}}}\)) are functions of the mean velocity. The Realizable k-\(\varepsilon\) (RKE) model is selected in this study due to its acceptable performance for these kinds of flow patterns [36, 37]. The model can be presented by using two relations for turbulence kinetic energy (TKE), k, based on the indicated assumptions, provided by:

$$\frac{\partial \left(\rho k{v}_{\rm i}\right)}{\partial {x}_{\rm i}}=\frac{\partial }{\partial {x}_{\rm i}}\left[\left(\mu +\frac{{\mu }_{\rm t}}{{\sigma }_{\rm k}}\right) \frac{\partial k}{\partial {x}_{\rm i}}\right]+\Gamma-\rho \varepsilon$$
(3)

and the dissipation rate of turbulent kinetic energy (ε), given by:

$$\frac{\partial \left(\rho \varepsilon {v}_{\rm i}\right)}{\partial {x}_{\rm i}}=\frac{\partial }{\partial {x}_{\rm i}}\left[\left(\mu +\frac{{\mu }_{\rm t}}{{\sigma }_{\varepsilon }}\right) \frac{\partial \varepsilon }{\partial {x}_{\rm i}}\right]+{C}_{1}\Gamma\varepsilon -{C}_{2}\frac{{\varepsilon }^{2}}{k+\sqrt{\nu \varepsilon }}$$
(4)

In these equations, \(\nu =\mu /\rho\) is the kinematic viscosity, and \(\Gamma\) is the turbulent kinetic energy production rate, given by:

$$\Gamma=-\overline{{v}_{\rm i}{v}_{\rm j}}\frac{\partial {v}_{\rm i}}{\partial {x}_{\rm j}}=\frac{{\mu }_{\rm t}}{\rho }\left(\frac{\partial {v}_{\rm i}}{\partial {x}_{\rm j}}+\frac{\partial {v}_{\rm j}}{\partial {x}_{\rm i}}\right)\frac{\partial {v}_{\rm i}}{\partial {x}_{\rm j}}$$
(5)

where the eddy viscosity (\({\mu }_{\rm t}\)) is formulated as:

$${\mu }_{\rm t}=\rho {C}_{\mu }\frac{{k}^{2}}{\varepsilon }$$
(6)

The constants of the RKE model (\({\sigma }_{\rm k}\), \({\sigma }_{\varepsilon }\), \({C}_{1}\), and \({C}_{2}\)) are given as:

$${\sigma }_{\rm k}=1.0$$
(7)
$${\sigma }_{\varepsilon }=1.2$$
$${C}_{1}=\mathrm{max}\left[0.43,\frac{{\mu }_{\rm t}}{{\mu }_{\rm{t}+5}}\right]$$
$${C}_{2}=1.0$$

Based on the above relations, the energy conservation equation reduces to:

$$\frac{\partial }{\partial {x}_{\rm i}}\left[{v}_{\rm i}\left(\rho E+P\right)\right]=\frac{\partial }{\partial {x}_{\rm j}}\left[\left(\lambda +\frac{{c}_{\rm p}{ \mu }_{\rm t}}{{Pr}_{\rm t}}\right)\frac{\partial T}{\partial {x}_{\rm j}}+{v}_{\rm i}{{\tau }_{\rm ij}|}_{\rm{eff}}\right]$$
(8)

where \({Pr}_{\rm t}\) is the Prandtl number of the turbulent flow, \({\tau }_{\rm ij}\) is the jth-direction shear stress, acting on a surface that is perpendicular to the ith-direction, and \({{\tau }_{\rm ij}|}_{\rm{eff}}\) is the deviatoric stress tensor, given by:

$${\left({\tau }_{\rm ij}\right)}_{\rm{eff}}=[{\mu }_{\rm{eff}}(\frac{\partial {v}_{\rm j}}{\partial {x}_{\rm i}}+\frac{\partial {v}_{\rm i}}{\partial {x}_{\rm j}})-\frac{2}{3}{\mu }_{\rm{eff}}\frac{\partial {v}_{\rm i}}{\partial {x}_{\rm j}}{\delta }_{\rm ij}]$$
(9)

where \(E\) is the total energy of the fluid, defined as:

$$E={c}_{\rm p}T-\left(\frac{P}{\rho }\right)+\left(\frac{{v}^{2}}{2}\right)$$
(10)

Here, \({\mu }_{\rm{eff}}\) is the molecular viscosity under turbulent conditions (\({\mu }_{\mathrm{eff}}=\mu +{\mu }_{\rm t}\)).

The entropy generation analysis is built based on the flow field’s thermo-hydraulic performance. The two causes of entropy generation in thermo-fluid systems are heat transfer and friction associated with fluid flow. This is presented as the thermal and viscous entropy production rates due to finite temperature gradients and finite velocity gradients, respectively. This incorporates the total entropy production rate equation, which indicates the amount of irreversibility within the system. The total volumetric entropy production rate (\({\dot{S}}_{\rm g}^{{{\prime}}{{\prime}}{{\prime}}}\)) is calculated from [12] as

$${\dot{S}}_{\rm g}^{\mathrm{^{\prime}}\mathrm{^{\prime}}\mathrm{^{\prime}}}={\dot{S}}_{\rm h}^{\mathrm{^{\prime}}\mathrm{^{\prime}}\mathrm{^{\prime}}}+{\dot{S}}_{\rm v}^{\mathrm{^{\prime}}\mathrm{^{\prime}}\mathrm{^{\prime}}}$$
(11)

where \({\dot{S}}_{\rm h}^{{{\prime}}{{\prime}}{{\prime}}}\) denotes the volumetric thermal entropy production rate (TEPR) and \({\dot{S}}_{\rm v}^{{{\prime}}{{\prime}}{{\prime}}}\) denotes the volumetric viscous entropy production rate (VEPR).

In the present study, the heat transfer from the tube to the surroundings is neglected, so that the entropy generation of the system is only due to the thermo-hydraulic interactions of the flowing fluid inside the tubes. To calculate the volumetric TEPR and VEPR, Eq. (12) and Eq. (13) are used [2, 31].

$${\dot{S}}_{\rm h}^{{{\prime}}{{\prime}}{{\prime}}}={\dot{S}}_{\rm{h},\overline{\rm T} }^{{{\prime}}{{\prime}}{{\prime}}}+{\dot{S}}_{\rm{h},{\rm T}^{^{\prime}}}^{{{\prime}}{{\prime}}{{\prime}}}=\frac{\lambda }{{\overline{T} }^{2}}\left[{\left(\frac{\partial \overline{T}}{\partial x }\right)}^{2}+{\left(\frac{\partial \overline{T}}{\partial y }\right)}^{2}+{\left(\frac{\partial \overline{T}}{\partial z }\right)}^{2}\right]+\frac{\lambda }{{\overline{T} }^{2}}\left[{\left(\frac{\overline{\partial {T }^{^{\prime}}}}{\partial x}\right)}^{2}+{\left(\frac{\overline{\partial {T }^{^{\prime}}}}{\partial y}\right)}^{2}+{\left(\frac{\overline{\partial {T }^{^{\prime}}}}{\partial z}\right)}^{2}\right]$$
(12)

Each of these parameters can be separated into mean and turbulent components in turbulent flow regimes. The RHS terms of Eq. (12) represent volumetric thermal entropy production rates due to mean temperature (\(\overline{T }\)) and turbulent temperature (\({T}^{^{\prime}}\)), respectively.

$${{\dot{S}}_{\rm v}}^{{{\prime}}{{\prime}}{{\prime}}}=\frac{\mu }{\overline{T} }\left.\left\{\begin{array}{c}{2[\left(\frac{\partial \overline{{v }_{\rm x}}}{\partial x}\right)}^{2}+{\left(\frac{\partial \overline{{v }_{\rm y}}}{\partial y}\right)}^{2}+{\left(\frac{\partial \overline{{v }_{\rm z}}}{\partial z}\right)}^{2}]\\ +{\left(\frac{\partial \overline{{v }_{\rm x}}}{\partial y}+\frac{\partial \overline{{v }_{y}}}{\partial x}\right)}^{2}+{\left(\frac{\partial \overline{{v }_{\rm x}}}{\partial z}+\frac{\partial \overline{{v }_{\rm z}}}{\partial x}\right)}^{2}+{\left(\frac{\partial \overline{{v }_{\rm y}}}{\partial z}+\frac{\partial \overline{{v }_{\rm z}}}{\partial y}\right)}^{2}\end{array}\right.\right\}+\frac{\rho \varepsilon }{\overline{T} }$$
(13)

The RHS terms of Eq. (13) represent volumetric viscous entropy production rates due to mean velocity (\(\overline{v }\)) and turbulent velocity (\({v}^{^{\prime}}\)), respectively. The thermal, viscous, and total entropy production rates are evaluated by integrating the volumetric entropy generation rates over the whole flow domain. This is provided by Eqs. (14) through (16), respectively.

$${\dot{S}}_{\rm h}=\iiint {\dot{S}}_{\rm h}^{{{\prime}}{{\prime}}{{\prime}}}\mathrm{d}\forall$$
(14)
$${\dot{S}}_{\rm v}=\iiint {\dot{S}}_{\rm v}^{{{\prime}}{{\prime}}{{\prime}}}\mathrm{d}\forall$$
(15)
$${\dot{S}}_{\rm g}=\iiint {\dot{S}}_{\rm g}^{{{\prime}}{{\prime}}{{\prime}}}\mathrm{d}\forall$$
(16)

where \(\forall\) is the volume of the mesh element.

Data reduction and performance indices

The present work investigated 198 different case studies based on tube geometrical configurations (straight, conical, smooth, or dimpled with different diameter ratios) and operating conditions (eleven values of Re within 3000 and 40,000). The Reynolds number Re formula is given by:

$$Re= \frac{\rho \overline{v} {D }_{\rm h}}{\mu }$$
(17)

where \({D}_{\rm h}\) is the hydraulic diameter and \(\overline{v }\) is the fluid mean velocity.

The contribution of the TEPR to the total entropy production rate is determined by the Bejan number Be, which is introduced as a dimensionless quantity, including the ratio of the TEPR to \({\dot{S}}_{\rm g}\) [32, 33]:

$$Be=\frac{\dot{{S}_{\rm h}}}{\dot{{S}_{\rm g}}}$$
(18)

The enhanced entropy generation ratio, Ns,en is defined as [34, 35, 38]

$${N}_{\rm{s,en}}=\frac{{\dot{S}}_{\rm g}}{{\dot{S}}_{\rm{g,smt}}}$$
(19)

where the subscript smt denotes smooth tubes with DR = 1.

The irreversibility distribution ratio \({\phi }_{\rm s}\) is defined as [10, 39]

$${\phi }_{\rm s}=\frac{\dot{{S}_{\rm v}}}{\dot{{S}_{\rm h}}}$$
(20)

CFD model development

The CFD model of various tube configurations is created in ANSYS-Fluent 2021 R1 [40], which uses the finite volume method to address the flow problem (FVM). For connecting the velocity and pressure flow fields, the SIMPLE method was used. The second-order upwind finite difference system was utilized for the discretization of convective terms, whereas the central difference finite difference scheme was used to handle diffusive terms. Iterations were stopped when the energy equation’s relative error was less than 10–8 and all other solved equations’ relative errors were less than 10–7.

Fluid properties, operating, and boundary conditions

Water has been utilized as a working fluid with a constant inlet temperature of 300 K. The thermophysical characteristics of water (density, dynamic viscosity, specific heat capacity, and thermal conductivity), depending on the local fluid temperature T [41], are given by:

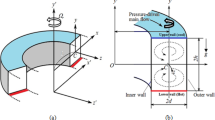
$$\begin{aligned} \rho & = 386.0722 + 5.4014 T - 0.0147 T^{2} + 1.1722 \times 10^{ - 5} T^{3} \,\,\left( {{\text{kg m}}^{{ - {3}}} } \right) \\ \mu & = 0.0695 - 5.7412 \times 10^{ - 4} T + 1.6025 \times 10^{ - 6} T^{2} - 1.5028 \times 10^{ - 9} T^{3} \,\,\left( {\text{Pa s}} \right) \\ c_{{\text{P}}} & = 6889.4 - 22.4418 T + 0.0602 T^{2} - 5.1784 \times 10^{ - 5} T^{3} \,\,\left( {{\text{J kg}}^{{ - {1}}} {\text{K}}^{{ - {1}}} } \right) \\ \lambda & = - 1.5298 + 0.015 T - 3.3883 \times 10^{ - 5} T^{2} + 2.5651 \times 10^{ - 8} T^{3} \,\,\left( {{\text{W m}}^{{ - {1}}} {\text{K}}^{{ - {1}}} } \right) \\ \end{aligned}$$
(21)

Figure 2b shows a description of the mathematical model of the tube heat exchanger, including various boundary conditions. All tube geometries under investigation are subjected to a uniform heat flux value of q" = 40 kW m−2 at their outer wall surfaces. No slip, as well as no penetration conditions, is applied to the inner walls of all tube configurations. As well as, the heat loss to the surrounding was neglected. Table 2 provides a summary of all boundary conditions, which were applied to the mathematical model.

Table 2 Summary of the applied boundary conditions
Full size table

Mesh generation

Tetrahedral finite volume elements were selected for generating the mesh of various tube configurations used in this study due to their suitability with complex geometries. Figure 3 illustrates details of the meshing domain for a dimpled conical tube with DR = 3. The mesh was refined near wall regions to accurately predict viscous and thermal boundary layer characteristics.

Fig. 3
figure 3

The meshing domain of dimpled conical tubes (a sample tube with DR = 1.5)

Full size image

To enhance the stability of the numerical solution of the flow domain and get independent grid generation with minimum computational time, a grid independence test is conducted by exploring the effect of mesh size reduction (number of elements increase) on different parameters of the computational domain. The grid independence test (GIT) has been studied for a dimpled convergent tube with DR = 1.5 at Re = 10,000, as shown in Fig. 4a. Eight different grid generations with numbers of 0.235314, 0.353613, 0.850759, 1.511956, 2.298282, 3.903664, 7.212474, and 9.173215 × 106 grids have been adopted during the test. The variations of two thermal performance parameters are shown in terms of the number of mesh elements, Nu and f. The two parameters, in the case of the grid number (3.903664 × 106), tend to stabilize with little deviation at about 3.903664 × 106 meshing elements with a percentage change of 0.12% and 0.75% for Nu and f, respectively, compared to the finest grid (9.173215 × 106). Consequently, it has been selected for the rest of the study.

Fig. 4
figure 4

a Grid independence test (GIT). b Validation of modeling straight smooth tube. c Validation of modeling straight tube with dimples. d Validation of straight smooth tube in terms of Bejan number against Bejan [42]

Full size image

Model validation

The established numerical model is validated against numerical and experimental studies, including dimpled and smooth tube configurations, available in the literature. Appendix A includes all the empirical correlations for the straight smooth tube to validate the present model. Figure 4b shows a comparison with correlations in terms of Nu for straight smooth tubes obtained by Dittus-Boelter [43], Sieder and Tate [44], and Gnielinski [45], with average errors of 6.63%, 3.35%, and 11.64%, respectively. Also, in terms of f, correlations by Petukhov [46], Filonenko, and Blasius [47] were used for the validation with average percentage deviations of 1.60%, 1.09%, and 1.92%, respectively. For straight dimpled tubes, the present model is validated against the results of Li et al. [14], as shown in Fig. 4c. The validation results in terms of Nu and f were estimated with average percentage deviations of 2.01% for Nu and 3.91% for f. Another validation of smooth straight tube was performed with the analytical solution of Bejan [42] in terms of Bejan number. A good agreement was observed, as presented in Fig. 4d, with an average deviation of about 6.912%. According to the various validation analysis, a good agreement of the model was obtained over the whole range of Re; hence, it can be used for the rest configurations proposed in the study.

Results and discussion

Fluid flow pattern analysis

The flow patterns of entropy generation parameters within different smooth and dimpled tube configurations are presented by the local thermal entropy and viscous entropy contours (Figs. 5 and 6). Figure 5 shows the TEPR contours for different convergent and divergent tube configurations with a DR of 1.5 at Re of 6,000. High TEPR intensities can be observed near the walls of all tube configurations, mainly due to the mean TEPR components. The centerline region possesses minimum thermal entropy production as bulk flows exist near isothermal conditions (internally reversible). By comparing TEPR values of smooth and dimpled tube geometries, all dimpled tubes show lower thermal entropy generation than the corresponding smooth tube geometries. This is due to the higher influence of thermal boundary layers on smooth tube geometries. In addition, higher uniform temperature distributions are associated with the presence of dimples.

Fig. 5
figure 5

Thermal entropy contours for various tube geometries at (\(\mathrm{Re}\) = 6000 and \(\mathrm{DR}\) = 1.5) with/without dimples

Full size image
Fig. 6
figure 6

Viscous entropy contours for various tube geometries at (\(\mathrm{Re}\) = 6000 and \(\mathrm{DR}\) = 1.5) with/without dimples

Full size image

Figure 6 shows the VEPR contours for different convergent and divergent tube configurations with DR of 1.5 at Re of 6000. As expected, the viscous entropy generation levels of all smooth tube configurations are lower than those for dimpled configurations due to the wakes and eddies in flow regions associated with the presence of dimples. Viscous boundary layers exist near the wall for all tube configurations where maximum shear stress and entropy values takes place. For smooth straight tubes, uniform distributions of VEPR exist along the entire flow direction. For convergent and divergent smooth tubes, maximum VEPR values exist near the walls of exit and inlet sections, respectively, due to higher flow velocities within these sections. For the straight tube with dimples, maximum entropy values are concentrated around dimpled regions all over the tube due to the extended no-slip condition. In addition, viscous entropy increases along the flow direction toward the tube outlet. Higher VEPR levels are associated with convergent dimpled tubes as flow acceleration takes place with maximum values at the convergent exit. Divergent dimpled geometries show maximum VEPR for about 50% of the tube, around dimpled surface areas, starting from the flow entrance. As the flow continues toward the diffuser outlet, much lower VEPR values are observed for the bulk of the flow.

Entropy generation performance analysis

Figure 7 shows variants of volumetric thermal, viscous, and total entropy generation rates over the whole Re range for smooth tubes with various DR. As Re increases, higher flow velocities and heat transfer rates are achieved with decreased TEPR levels for all tube configurations. For convergent smooth tubes with DR of 1.5 to 5, the average TEPR spans from 0.77 to 0.12 W K−1 for Re = 3000 to 40,000, respectively. Maximum TEPR values are associated with the straight smooth tube, ranging from 0.83 to 0.14 W K−1 for Re = 3000 to 40,000, respectively, due to higher concentrations within the tube boundary layer. Smooth divergent tubes keep the same trend of decreasing TEPR with increased Re, but with higher entropy generation rates. For instance, smooth divergent tubes with DR = 1.5 show a TEPR variation of 0.87 to 0.17 W K−1 for Re = 3000 to 40,000, respectively, while smooth divergent tubes with DR = 5 show a TEPR variation of 1.15 to 0.36 W K−1 for Re = 3000 to 40,000, respectively. For the variation of the VEPR with increased Re, the trend is increasing for all smooth tube geometries. Furthermore, for convergent smooth tubes, VEPR increases as DR increases. At Re = 40,000, the minimum VEPR value is 0.0016 W K−1 for the smooth convergent tube with DR = 1.5, while the maximum VEPR value is 0.0415 W K−1 for smooth convergent tubes with DR = 5. For smooth divergent tubes, VEPR levels are lower as compared to the corresponding convergent configurations, with an average value of 0.00015 W K−1 over the whole range of Re. As discussed earlier, the total EPR is mostly due to the contribution of the TEPR as VEPR values are much lower in magnitude. A maximum total EPR value of 0.78 W K−1 is achieved with smooth convergent tubes of DR = 5 at Re = 3000, while smooth divergent tubes with the same DR and Re showed a maximum total EPR value of 1.20 W K−1.

Fig. 7
figure 7

Variations of entropy generation components; a Thermal, b viscous, and c total entropy generation for smooth tubes with different diameter ratios DR

Full size image

Figure 8 shows different dimensionless performance indices of the entropy generation analysis for smooth tube configurations as functions of the Re. This includes Be, Ns,en, and \({\phi }_{\rm s}\). The variation trend for Be is decreasing with increased Re, for all tube configurations. This is due to the increase of \({\dot{S}}_{v}\) contribution on the account of \({\dot{S}}_{h}\) with increased flow velocities. For straight smooth tubes, the variation in Be is negligible over the whole Re range (within 0.6%). For convergent smooth tubes, with increased DR, Be decreases for the same Re. For convergent smooth tubes with DR of 5, the change in Be is from 1.0 to 0.73, respectively, at Re = 3,000 to 40,000, with a maximum change of 27% among all DR values. For smooth divergent tubes, the change in Be is almost independent of DR and Re, with an average value of 0.9994. The enhanced entropy generation ratio, Ns,en, for smooth convergent tubes with all DR is less than unity over the whole operating range of Re, especially for tubes with DR = 1.5–3. The average values of Ns,en for convergent smooth tubes with DR of 1.5–3 are 0.93 and 0.83 at Re = 3,000 and 40,000, respectively. This performance can be interpreted in terms of the total entropy generation for smooth convergent tubes (Fig. 7), which decreases as Re increases, especially for Re > 20,000. The maximum value of Ns,en for smooth convergent tubes is 1.08, achieved with DR = 5. For smooth divergent tubes, all values of Ns,en are above unity for all DR values over the whole range of Re. This is due to the elevated total EPR values for divergent smooth geometries, as compared to the convergent smooth ones. Ns,en values for smooth divergent tubes increase with increasing both Re and DR. For smooth divergent tubes with DR = 1.5, values of Ns,en are 1.05 and 1.21 at Re = 3,000 and 40,000, respectively. Maximum Ns,en values are attained with smooth divergent tubes with DR = 5: 1.44 and 2.53 at Re = 3,000 and 40,000, respectively. The variation of the irreversibility distribution ratio, \({\phi }_{\rm s}\), for smooth convergent tubes, is increasing with the increase of Re and DR, as expected due to the increase of VEPR with these two parameters. For the smooth straight tube as well as smooth convergent tubes with DR = 1.5 and 2, there is no significant increase in \({\phi }_{\rm s}\) over the whole range of Re with an average value of \({\phi }_{\rm s}\) = 2.75 × 10–3. The maximum values of \({\phi }_{\rm s}\) for smooth convergent tubes with DR = 3 and DR = 5 are found to be 0.086 and 0.370, respectively, at Re = 40,000. For smooth divergent tubes, as expected, there is no significant increase in \({\phi }_{\rm s}\) with the variations of DR and Re with an average value of 7.16 × 10–4, due to reduced flow velocities.

Fig. 8
figure 8

Variations of different dimensionless performance indices of entropy generation analysis; a Be, b Ns,en, and c \({\phi }_{\mathrm{s}}\) for smooth tubes with various DR

Full size image

Figure 9 shows variations of thermal, viscous, and total entropy generation rates throughout the entire range of Re for tubes with dimples having various DR values. As for the case of all smooth tube geometries, the TEPR decreases with the increase in Re. The straight dimpled tube records a variation in TEPR of 0.42 to 0.10 W K−1 over the whole range of Re, from 3000 to 40,000, with a reduction of 48.9% to 25.1%, respectively, as compared to the TEPR of smooth straight tubes. Convergent dimpled tubes show a further reduction in the TEPR with increasing DR, as compared to smooth convergent ones. For convergent dimpled tubes with DR = 5, a reduction in the TEPR from 0.39 to 0.07 W K−1 at Re = 3000 to 40,000, respectively. This represents the maximum reduction in TEPR for dimpled tube geometries with a percentage of − 50.4 to 25.3, respectively, as compared to the TEPR of smooth convergent tubes with the same DR. Divergent dimpled tubes show relatively higher TEPR values as compared to convergent dimpled tubes, but lower TEPR values are achieved when compared to the corresponding smooth geometries. Maximum TEPR values for divergent dimpled tubes range from 1.13 to 0.29 W K−1 at Re = 3000 to 40,000 with DR = 5 with a reduction of 1.7% to 19.4%, respectively. VEPR values for dimpled tube geometries are higher as compared to smooth tube geometries, also in an increasing fashion with increased Re and DR values. Convergent dimpled tubes with DR of 5 have the maximum VEPR value of 0.19 at Re = 40,000 with an increase of 400% as compared to smooth convergent ones. Overall, the total EPR values for dimpled tube geometries are lower than those for the corresponding smooth ones, especially for convergent dimpled tubes. Convergent dimpled tubes with DR = 1.5–3 show the lowest total EPR values over the whole Re range with an average value of 0.20, as compared to an average value of 0.34 W K−1 for the corresponding smooth configurations. The maximum value of the total EPR attained with dimpled convergent tubes of DR = 1.5 is 0.39 W K−1 at Re = 3000. This value is 53.6% less than the total EPR value for smooth convergent tubes with the same DR and at the same Re. Divergent dimpled tubes with DR = 5 showed the maximum total EPR value of 1.13 W K−1 at Re = 3000, which is 5.8% less than that of smooth divergent tubes (Fig. 10).

Fig. 9
figure 9

Variations of entropy generation components; a thermal, b viscous, and c total entropy generation for dimpled tubes with different diameter ratios DR

Full size image
Fig. 10
figure 10

Variations of different dimensionless performance indices of entropy generation analysis; a Be, b Ns,en, and c \({\phi }_{\mathrm{s}}\) for dimpled tubes with various DR

Full size image

Figure 8 shows different dimensionless performance indices of the entropy generation analysis for dimpled tube configurations as functions of the Re. As compared to smooth tubes, the changes in Be for the corresponding dimpled tubes are higher across the whole range of Re. For straight dimpled tubes, the change in Be is − 7.2%, as compared to − 0.59% for the straight smooth tube, over the entire range of Re. For convergent dimpled tubes with DR = 5, the change in Be is − 71.2%, as compared to − 27% for the convergent smooth tube, over the entire range of Re. For dimpled divergent tubes, the change in Be is almost independent of DR and Re, with an average value of 0.9952. For the dimpled straight tube and dimpled convergent tubes with DR = 1.5–3, Ns,en values are less than unity over the whole operating range of Re. This is also valid for dimpled convergent tubes with DR = 5 for Re values up to 30,000. Unlike the case of smooth convergent tubes with DR = 1.5–3, the values of Ns,en always increase with increased Re. The average values of Ns,en for dimpled convergent tubes with DR = 1.5–3 are 0.46 and 0.80 at Re = 3000 and 40,000, respectively. This means reductions of 50.54% and 3.61% at both Re values, respectively. The dimpled convergent tube with DR = 2 achieved the lowest average value of Ns,en = 0.55 compared to a value of 0.86 for the smooth tube, over the whole Re range, with a reduction of 36.05%. The maximum value of Ns,en for dimpled convergent tubes is 1.83, attained with those with DR = 5, compared to 1.08 for smooth convergent tubes with the same DR. Dimpled straight tubes and dimpled divergent tubes with DR = 1.5–2 have Ns,en values lower than unity for almost all of the Re range. Ns,en values for dimpled divergent tubes increase with increasing both Re and DR. Minimum Ns,en values are attained with straight dimpled tubes: 0.50 and 0.78 at Re = 3000 and 40,000, respectively. Maximum Ns,en values are attained with dimpled divergent tubes with DR = 5: 1.36 and 2.07 at Re = 3000 and 40,000, respectively. As for smooth convergent tubes, the variation of \({\phi }_{\rm s}\) for dimpled convergent tubes is increasing with the increase of Re and DR. For the dimpled straight tube as well as dimpled convergent tubes with DR = 1.5 and 2, there is no significant increase in \({\phi }_{\rm s}\) over the whole range of Re with an average value of \({\phi }_{\rm s}\) = 3.40 × 10–2. The maximum values of \({\phi }_{\rm s}\) for dimpled convergent tubes with DR = 3 and DR = 5 are found to be 0.723 and 2.480, respectively, at Re = 40,000. For dimpled divergent tubes, there is no significant increase in \({\phi }_{\rm s}\) with the variations of DR and Re with an average value of 3.58 × 10–3, a little bit higher than the value for smooth divergent tubes due to the presence of dimples.

Conclusions

A comprehensive entropy generation analysis based on the thermo-hydraulic performance of turbulent flows inside dimpled conical tubes of different diameter ratios was performed in the present study. The performance of different dimpled tube configurations and flow modes was numerically investigated and compared against straight/conical smooth tubes to optimize their thermal design and control their entropy generation behavior. The following are the main conclusions of the present numerical study:

  • A maximum total EPR value of 0.78 W K−1 is achieved with smooth convergent tubes of DR = 5 at Re = 3000, while smooth divergent tubes with the same DR and Re showed a maximum total EPR value of 1.20 W K−1.

  • For convergent smooth tubes, with growing the DR, Be decreases for the same Re. For smooth convergent tubes with DR = 5, the change in Be is from 1.0 to 0.73, respectively, at Re = 3000 to 40,000, with a maximum change of 27% among all DR values. For smooth divergent tubes, the change in Be is almost independent of DR and Re, with an average value of 0.9994.

  • The enhanced entropy generation ratio, Ns,en, for smooth convergent tubes with all DR is less than unity over the whole operating range of Re, especially for tubes with DR = 1.5–3. The average values of Ns,en for smooth convergent tubes with DR = 1.5–3 are 0.93 and 0.83 at Re = 3000 and 40,000, respectively.

  • The variation of the irreversibility distribution ratio, \({\phi }_{\rm s}\), for smooth convergent tubes, is increasing with the increase of Re and DR, as expected due to the increase of VEPR with these two parameters.

  • Total entropy production rate values for dimpled tube geometries are lower than those for the corresponding smooth ones, especially for convergent dimpled tubes.

  • Dimpled convergent tubes with DR = 1.5–3 show the lowest total EPR values over the whole Re range with an average value of 0.20, as compared to an average value of 0.34 W K−1 for the corresponding smooth configurations.

  • The maximum value of the total EPR attained with dimpled convergent tubes of DR = 1.5 is 0.39 W K−1 at Re = 3000. This value is 53.6% less than the total EPR value for smooth convergent tubes with the same DR and at the same Re.

  • Dimpled divergent tubes with DR = 5 showed the maximum total EPR value of 1.13 W K−1 at Re = 3000, which is 5.8% less than that of smooth divergent tubes.

  • The changes in Be for dimpled tubes are higher across the entire Re range, in reference to the corresponding smooth ones.

  • For the dimpled straight tube and dimpled convergent tubes with DR = 1.5–3, Ns,en values are less than unity over the whole operating range of Re. The average values of Ns,en for dimpled convergent tubes with DR = 1.5–3 are 0.46 and 0.80 at Re = 3000 and 40,000, respectively. This means reductions of 50.54% and 3.61% at both Re values, respectively.

  • For the dimpled straight tube as well as dimpled convergent tubes with DR = 1.5 and 2, there is no significant increase in \({\phi }_{\rm s}\) over the whole range of Re with an average value of \({\phi }_{\rm s}\) = 3.40 × 10–2. The maximum values of \({\phi }_{\rm s}\) for dimpled convergent tubes with DR = 3 and DR = 5 are found to be 0.723 and 2.480, respectively, at Re = 40,000.

For all studied flow cases of all tube configurations and based on the extensive entropy generation evaluation, convergent dimpled tubes provided maximum heat transfer rates with an acceptable level of friction and minimum entropy generation rates. Convergent dimpled tubes with DR = 1.5–3 recorded the best performance all over the whole operating range of Re. Therefore, it can be concluded that utilizing such types of geometrical enhancement will lead to better energy and CO2 savings as well as a more compact design of heat exchangers. As a promising combination of the conical tubes, especially the convergent ones with/without dimples in terms of thermo-hydraulic characteristics, many extended studies can be carried out in the future like using other shapes of turbulators, using nanofluids instead of water as a working fluid, and others.