MHD unsteady GO–water-squeezing nanofluid flow—heat and mass transfer between two infinite parallel moving plates: analytical investigation

Abstract

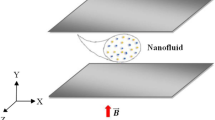
Investigation for unsteady squeezing viscous flow is one of the most important research topics due to its wide range of engineering applications such as polymer processing and lubrication systems. The aim of the present paper is to study the unsteady squeezing viscous graphene oxide–water nanofluid flow with heat transfer between two infinite parallel plates. The governing equations, continuity, momentum and energy for this problem are reduced to coupled nonlinear ordinary differential equations using a similarity transformation. The transmuted model is shown to be controlled by a number of thermo-physical parameters, viz., moving parameter, graphene oxide nanoparticles solid volume fraction, Eckert and Prandtl numbers. Nusselt number and skin friction parameter are obtained for various values of GO solid volume fraction and Eckert number. Comparison between analytical results and numerical ones achieved by fourth order Runge–Kutta method revealed that our analytical method can be a simple, powerful and efficient technique for finding analytical solutions in science and engineering nonlinear differential equations.

Appendix: Application of VIM

Using the proposed procedure for variational iteration method (VIM) to solve Eq. (8) with the associated boundary conditions (11), we have the following iterative schemes:

$$ f_{n + 1} = f_{n} - \int\limits_{0}^{\eta } {\frac{{\left( {s - \eta } \right)^{3} }}{3!}\left[ \begin{aligned} f_{n}^{{\left( {IV} \right)}} \left( s \right) - S\left( \begin{aligned} &sf_{n}^{{{\prime \prime \prime }}} \left( s \right) + 3f^{\prime\prime}_{n} \left( s \right) \hfill \\ & + f_{n}^{{\prime }} \left( s \right)f_{n}^{{\prime \prime }} \left( s \right) - f_{n}^{{{\prime \prime \prime }}} \left( s \right)f_{n} \left( s \right) \hfill \\ \end{aligned} \right) \hfill \\ - Ha^{2} f^{{\prime \prime }} \left( s \right)_{n} \hfill \\ \end{aligned} \right]} ds $$

(20)

The first two approximants of the solutions are given by

$$ \begin{aligned} f_{0} \left( \eta \right) & = A + \frac{1}{2}A_{1} \eta^{2} + \frac{1}{6}A_{2} \eta^{3} , \\ f_{1} \left( \eta \right) & = A + \frac{1}{2}A_{1} \eta^{2} + \frac{1}{6}A_{2} \eta + \left( { - \frac{1}{12}SAA_{2} + \frac{1}{8}SA_{1} + \frac{1}{24}M^{2} A_{1} } \right)\eta^{4} \\ & \quad + \left( {\frac{1}{30}SA_{2} + \frac{1}{120}M^{2} A_{2} } \right)\eta^{5} - \frac{1}{360}SA_{1} A_{2} \eta^{6} - \frac{1}{2520}SA_{2}^{2} \eta^{7} . \\ \end{aligned} $$

(21)

According to boundary conditions we know, $f\left( 0 \right) = 0$. Therefor $A = 0$. We can find further approximants of the solutions in a similar fashion. It is important to note that the same trend can be used for non-dimensional energy and concentration equations.