Modified enthalpy method for the simulation of melting and solidification

Abstract

Enthalpy method is commonly used in the simulation of melting and solidification owing to its ease of implementation. It however has a few shortcomings. When it is used to simulate melting/solidification on a coarse grid, the temperature time history of a point close to the interface shows waviness. While simulating melting with natural convection, in order to impose no-slip and impermeability boundary conditions, momentum sink terms are used with some arbitrary constants called mushy zone constants. The values of these are very large and have no physical basis. Further, the chosen values affect the predictions and hence have to be tuned for satisfactory comparison with experimental data. To overcome these deficiencies, a new cell splitting method under the framework of the enthalpy method has been proposed. This method does not produce waviness nor requires mushy zone constants for simulating melting with natural convection. The method is then demonstrated for a simple one-dimensional melting problem and the results are compared with analytical solutions. The method is then demonstrated to work in two-dimensions and comparisons are shown with analytical solutions for problems with planar and curvilinear interfaces. To further benchmark the present method, simulations are performed for melting in a rectangular cavity with natural convection in the liquid melt. The solid–liquid interface obtained is compared satisfactorily with the experimental results available in literature.

Appendices

Appendix A

In this section, we prove that the interface constructed is second order accurate. Let Γ(x, y) = 0 denote the equation of the actual interface. Consider the situation shown in figure 14. We assume that in the neighbourhood of x = 0 the curve Γ(x, y) can be written as, y = f(x). Let y = g(x) = mx + c denote the straight line approximation to this curve.

Figure 14

The error analysis for interface construction method.

The error e will be defined as the distance between the points A and B in figure 14. The error is thus

$$\label{a1} e=\left| {g(0)-f(0)} \right|=\left| {c-f(0)} \right|. $$

(57)

The approximate interface g(x) will be chosen by the present interface construction method such that ratio in which it divides the control volumes ‘P’ and ‘E’ are same as that by f(x).

The above mentioned conditions will hold true only if f(x) and g(x) intersect each other at least once in ‘P’ and ‘E’.

Let x _a and x _b denote these points of intersection such that 0 < x _b < h and − h < x _a < 0, where h denotes the dimension of the control volume in the x direction. By Taylor series

$$\label{a2} f(x)=f(0)+\frac{f^\prime (0)}{1!}x+\frac{f^{\prime\prime} (0)}{2!}x^2+...... $$

(58)

At the points x _a and x _b

$$\label{a3} {\begin{array}{*{20}c} {f(x_a )=g(x_a )} \\ {f(x_b )=g(x_b ).} \\ \end{array} } $$

(59)

Thus,

$$\label{a4} mx_a +c=f(0)+\frac{f^\prime (0)}{1!}x_a +\frac{f^{\prime\prime} (0)}{2!}x_a^2 +...... $$

(60)

$$\label{a5} mx_b +c=f(0)+\frac{f^{\prime} (0)}{1!}x_b +\frac{f^{\prime\prime} (0)}{2!}x_b^2 +...... $$

(61)

Multiplying equation (60) by x _b and equation (61) by x _a and subtracting,

$$\label{a6} \left( {x_b -x_a } \right)\left( {c-f(0)} \right)=\frac{f^{\prime \prime} (0)}{2!}x_a x_b \left( {x_b -x_a } \right)+......+\frac{f^n(0)}{n!}x_a x_b \left( {x_b^n -x_a^n } \right). $$

(62)

The above equation can be simplified into,

$$\label{a7} c-f(0)=\frac{f^{\prime \prime} (0)}{2!}x_a x_b +......+\frac{f^n(0)}{n!}x_a x_b \left( {\sum\limits_0^{n-2} {x_a^r x_b^{n-2-r} } } \right). $$

(63)

Taking the modulus of the function

$$\label{a8} \left| {c-f(0)} \right|\le \left| {\frac{f^{\prime \prime} (0)}{2!}x_a x_b } \right|+......+\left| {\frac{f^n(0)}{n!}x_a x_b \left( {\sum\limits_0^{n-2} {x_a^r x_b^{n-2-r} } } \right)} \right|+...... $$

(64)

Since

$$\label{a9} \left| {x_a } \right|\le h\quad \mbox{and}\quad \left| {x_b } \right|\le h, $$

(65)

$$\label{a10} \left| {c-f(0)} \right|\le \left| {\frac{f^{\prime\prime} (0)}{2!}} \right|h^2+......+\left| {\frac{f^n(0)}{\left( {n-1} \right)!}} \right|h^n+......\ . $$

(66)

Thus from equations (57) and (66)

$$\label{a11} e=O(h^2). $$

(67)

Appendix B

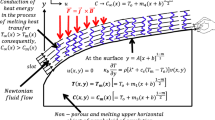
In this section, the form taken by the present cell splitting method for one-dimension situation is presented. The significant differences between the present scheme and the explicit enthalpy scheme of Tacke (1985) which eliminate waviness are also highlighted. Consider a stencil of control volume as show in figure 15. The solid–liquid interface is assumed to be present in the control volume ‘P’ while control volume ‘E’ is liquid and ‘W’ is solid. The centroids of the liquid and the solid control volumes are denoted by X ^L and X ^S, respectively. The liquid fractions at the east and the west face of the control volume are denoted by f _e and f _w , respectively. For the sake of clarity, the temperatures in the solid and the liquid domain are distinguished by the superscripts ‘S’ and ‘L’, respectively.

Figure 15

The stencil for the control volume discretisation.

The differential form of the energy equation for the liquid domain obtained by suitably substituting for ϕ in equation (11) is

$$\label{b1} .\frac{d}{dt}\int\limits_V {\rho C_P \left( {T^L-T_M } \right)} dV=\int\limits_A {k\nabla T^L.\hat{{n}}dA} +\int\limits_{A_I } {k\nabla T^L.\hat{{n}}dA} . $$

(68)

Equation (68) can be discretised for the control volume shown in figure 15 as

$$\label{b2} a_P^L T_P^L =a_E^L T_{E }^L +a_W^L T_{W }^L +a_I^L T_M +b, $$

(69)

where

$$\label{b3} a_E^L =f_e \frac{k}{x_E^L -x_P^L }, \quad a_W^L =f_w \frac{k}{x_P^L -x_W^L }, $$

(70)

$$\label{b4} a_I =\left\{ {{\begin{array}{*{20}c} {\frac{k}{x_I -x_P^L }} &\quad {0 < f_p < 1} \\[6pt] 0 &\quad {f_P =0, f_P =1} \\ \end{array} }} \right. $$

(71)

$$\label{b5} a_P^L =a_E^L +a_W^L +a_I^L +\frac{\rho C_P f_P \Delta x_P }{\Delta t} $$

(72)

$$\label{b6} b=\frac{\rho C_P f_P \Delta x_P }{\Delta t}T_M +\frac{\rho C_P f^O_P \Delta x_P }{\Delta t}\left( {T^{O^{L}}-T_M}\right). $$

(73)

In the above equations the superscript ‘O’ denotes the values in the previous time steps and Δx _P denotes the width of the control volume ‘P’ in figure 15. In the situation shown in figure 15 where the liquid is not present on the east face $a_E^L =0$. A similar equation can be derived to obtain the temperature in the solid domain.

The enthalpy form of the energy equation (12) is

$$\label{b7} \frac{d}{dt}\mathop{\int}\limits_{V} {\rho h} dV + \mathop{\int}\limits_{A_{\rm C}} {\rho h{\rm {\bf V}}}.\hat{n} dA=\mathop{\int}\limits_{A_{\rm C}} {k\nabla T.\hat{n}} dA. $$

(74)

which can be written in a discrete form of as

$$\label{b8} \rho \frac{h_P -h_P^O }{\Delta t}=a_{E }^L \left( {T_E^L -T_P^L } \right)+a_{E }^S \left( {T_E^S -T_P^S } \right)+a_W^L \left( {T_W^L -T_P^L } \right)+a_W^S \left( {T_W^S -T_P^S } \right), $$

(75)

where $a_E^S$ and $a_W^S$ the coefficients obtained by solving the energy equation in the solid domain. From the enthalpy equation the liquid fraction can be recovered from,

$$\label{b9} h_P =C_P f_P \left( {T_P^L -T_M } \right)+C_P \left( {1-f_P } \right)\left( {T_P^S -T_P } \right)+f_P \Delta H_M , $$

(76)

which asserts that the enthalpy of a control volume is composed of its sensible and latent heat parts.

Tacke (1985) had proposed an explicit enthalpy scheme which eliminates waviness in the enthalpy method. The significant difference between the schemes of the present cell splitting method with that of Tacke (1985) are

• (a) In the method by Tacke (1985) the diffusive flux on the west face of the control volume for e.g., was discretised as

  $$\label{b10} Q_W = -k\frac{T_M - T_W}{X_I - X_W}, $$

  (77)

  while in the present method the diffusive flux is discretised as

  $$\label{b11} Q_W = -k\frac{T_P^L - T_W}{X_P^L - X_W}. $$

  (78)

• (b) In the method by Tacke (1985) the temperature of the solid and liquid domains which are necessary to calculate the sensible heat in the equation (76) are obtained by linear interpolation of the temperatures T _M , T _E and T _M , T _W . While in the present method these temperature are obtained by solving the energy equation (69).

Nomenclature

• A   Area of a face of a control volume, m²

• A _I    Area of the interface part of a control volume, m²

• A _C   Area of the Cartesian part of a control volume, m²

• a   Coefficients appearing in a transport equation

• b   Source term in discretised equation

• C _P    Specific heat, J/kg-K

• C   y intercept of the constructed interface, m

• D   Net diffusion into a control volume

• d   Coefficients appearing in a diffusion equation

• e   Error between the actual and the predicted location of the interface

• f   Liquid fraction

• f (x)   Equation of the interface

• F _PX F _PY    Force due to pressure in x and y direction, N

• g   Acceleration due to gravity, m/s²

• g(x)   Equation of the constructed interface

• H   Enthalpy, J/kg

• h   Width of the control volume in appendix A, m

• k   Thermal conductivity, W/m-K

• L _S    A characteristic length scale, m

• m   Slope of the constructed interface

• N   Direction normal to the solid–liquid interface, m

• $\hat{n}$   Unit vector normal to a face

• P   Pressure, N/m²

• P′   Pressure correction, N/m²

• Q   Strength of a line heat source, W/m

• q _D    Net diffusion into a control volume

• r   Radial coordinate, m

• r ^∗   Non-dimensional radial coordinate

• R   Radial location of the solid–liquid interface, m

• R ^∗   Radial location of the solid–liquid interface in non-dimensional form

• S   Volumetric source terms in a transport equation

• S(τ)   Non-dimensional position of the solid–liquid interface along the x direction

• S _S    Source term due to secondary gradient in transport equation

• S _SP    Source term due to secondary gradient in pressure, m/s

• s(t)   Position of the solid–liquid interface along the x direction, m

• T   Temperature, K

• T _ref    A reference temperature, K

• T _M    Melting point temperature, K

• T _W    Temperature at the wall, K

• t Time, s

• (u,v )   Velocity coordinates, m/s

• $\tilde{u},\tilde{v}$   Tilde velocity used in momentum interpolation, m/s

• V   Volume of a control volume, m³

• V   Velocity vector, m/s

• V $_{\textbf{g}}$   Velocity of the grid, m/s

• X   Non-dimensional coordinate along x axis

• (x,y)   Coordinate axis, m

• (x _a ,x _b )   x location of the points at which the constructed interface intersects the actual interface

• ΔH _M    Latent heat of melting, J/kg

• ΔV   Volume of a control volume, m³

Non-dimensional numbers

• Pr   Prandtl number

• Ra   Rayleigh number

• St   Stefan number

Greek Symbols

• α   Thermal diffusivity, m²/s

• β   Volumetric expansion coefficient, 1/K

• Γ(x, y)   Equation of the interface

• θ   Non-dimensional temperature

• θ _a , θ _b    Non-dimensional temperatures at the start and end of a wavy cycle respectively

• λ   A constant appearing in equation (55)

• μ   Dynamic viscosity, Pa-s

• ν   Kinematic viscosity, m²/s

• ξ   A coordinate along the line joining the centroids of the control volumes, m

• ρ   Density, kg/m³

• τ   Non-dimensional time

• τ _a , τ _b    Non-dimensional times at the start and end of a wavy cycle respectively

• τ*   Non-dimensional time at which the interface is at the centroid of the control volume

• τ**   Non-dimensional time when the one dimension melting system reaches pseudo steady state as predicted by classical enthalpy method

• Φ   A generic transport variable

• Ω   The domain

Subscripts

• E,W,N,S   Tags used to address the neighbours of chosen control volume

• e,w,n,s   Tags used to address the faces of chosen control volume

• f   Face

• I   Interface

• nb   Neighbours

• P   A tag used to address a chosen control volume

• n   Normal

• x,y, ξ   Partial derivatives along the corresponding directions

• S   Solid

• L   Liquid

Subscripts

• S   Solid

• L   Liquid

Abbreviations

• CV   Control Volume

• SL   Solid–liquid