Periodic solutions of the modified short pulse equation

Abstract

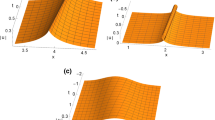
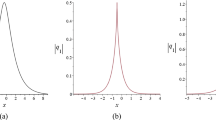
With the aid of the reciprocal transformation between the modified short pulse (mSP) equation and the sine-Gordon (sG) equation, certain periodic solutions of the mSP equation are constructed. Both one-phase and two-phase periodic solutions are presented. Taking the proper limits of those periodic solutions, various solitary wave solutions such as one-cuspon, two-cuspon and one-breather solutions are recovered. In addition, three novel standing wave solutions for the mSP equation are obtained.

Appendix A. The definitions and properties of elliptic functions

Here, we list some relevant definitions and properties of elliptic functions. For more details, one may consult the book of Lawden [22].

DEFINITION A.1

The elliptic integral of the first kind is defined as follows:

$$\begin{aligned}{} & {} \textrm{sn}^{-1}(x,k)=u=\int _{0}^{x}{\{(1-t^2)(1-k^2t^2)\}}^{-\frac{1}{2}}\textrm{d}t \nonumber \\{} & {} \quad (0\le x \le 1). \end{aligned}$$

(A.1)

DEFINITION A.2

Jacobi’s elliptic integral E(u, k) is defined as

$$\begin{aligned}{} & {} E(u,k)=\int _{0}^{u}{\textrm{dn}^2{v}}\,\textrm{d}v=\int _{0}^{\tau }{\sqrt{\frac{1-k^2t^2}{1-t^2}}}\textrm{d}t\nonumber \\{} & {} \quad (t=\textrm{sin}\,{v},\tau =\textrm{sn}\,{u}). \end{aligned}$$

(A.2)

The periodicity relation is

$$\begin{aligned} E(u+2K,k)=E(u,k)+2E(k). \end{aligned}$$

(A.3)

More generally, if m is an integer, then we have

$$\begin{aligned} E(u+2mK,k)=E( u,k)+2m E(k). \end{aligned}$$

(A.4)

DEFINITION A.3

The first complete elliptic integral is defined as

$$\begin{aligned} K \equiv K(K,k)\equiv K(k)=\int _{0}^{\frac{\pi }{2}}{\frac{1}{\sqrt{1-k^2 \,\textrm{sin}^2{\theta }}}}\textrm{d}\theta . \nonumber \\ \end{aligned}$$

(A.5)

DEFINITION A.4

The second complete elliptic integral is defined as

$$\begin{aligned} E \equiv E(K,k)\equiv E(k)=\int _{0}^{\frac{\pi }{2}}{\sqrt{1-k^2 \,\textrm{sin}^2\,{\theta }}}\,\textrm{d}\theta . \nonumber \\ \end{aligned}$$

(A.6)

As demonstrated in [22], the following formulas hold:

$$\begin{aligned}{} & {} \begin{aligned}&\int {\textrm{cn}^2(u,k)}\textrm{d}u=\frac{1}{k^2}(E(u,k)-k'^2 u),\\&\int {\frac{1}{\textrm{cn}^2(u,k)}}\textrm{d}u=\frac{1}{k'^2}\\&\quad \times \bigg (\frac{\textrm{sn}(u,k)\textrm{dn}(u,k)}{\textrm{cn}(u,k)}-{E(u,k)+k'^2 u}\bigg ), \end{aligned} \end{aligned}$$

(A.7)

$$\begin{aligned}{} & {} \begin{aligned}&\int {\frac{\textrm{sn}^2(u,k)}{\textrm{cn}^2(u,k)}}\textrm{d}u=\frac{1}{k'^2}\\&\quad \times \bigg (\frac{\textrm{dn}(u,k)\textrm{sn}(u,k)}{\textrm{cn}(u,k)}-\int {\textrm{dn}^2(u,k)}\textrm{d}u\bigg ),\\&\int {\frac{1}{\textrm{dn}^2(u,k)}}\textrm{d}u=\frac{1}{k'^2}\\&\quad \times \bigg (-k^2\frac{\textrm{sn}(u,k)\textrm{cn}(u,k)}{\textrm{dn}(u,k)}+\int {\textrm{dn}^2(u,k)}\textrm{d}u\bigg ), \end{aligned} \end{aligned}$$

(A.8)

where $k'=\sqrt{1-k^2}$.

In the extreme cases $k = 0, 1$, we have

$$\begin{aligned}&\textrm{sn}(u,0)=\sin u, \end{aligned}$$

(A.9)

$$\begin{aligned}&\textrm{cn}(u,0)=\cos u, \end{aligned}$$

(A.10)

$$\begin{aligned}&\textrm{dn}(u,0)=1, \end{aligned}$$

(A.11)

$$\begin{aligned}&\textrm{sn}(u,1)=\textrm{tanh}\, u, \end{aligned}$$

(A.12)

$$\begin{aligned}&\textrm{cn}(u,1)=\textrm{sech}\, u, \end{aligned}$$

(A.13)

$$\begin{aligned}&\textrm{dn}(u,1)=\textrm{sech}\, u, \end{aligned}$$

(A.14)

$$\begin{aligned}&E(u,1)=\textrm{tanh}(u). \end{aligned}$$

(A.15)