Skip to main content

A parametric model to study the mass–radius relationship of stars

Pramana volume 92, Article number: 43 (2019) Cite this article

Abstract

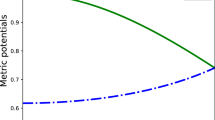
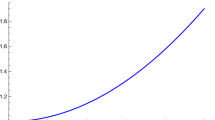
In static space–time, we solve the Einstein–Maxwell equations. The effective gravitational potential and the electric field for charged anisotropic fluid are defined in terms of two free parameters. For such configurations, the mass of the star as a function of stellar radius is found in terms of two aforementioned parameters subjected to certain stability criteria. For various values of these two parameters, one finds that such a mass–radius relationship can model stellar objects located at various regions of the Hertzsprung–Russel diagram.

This is a preview of subscription content, access via your institution.

Access options

Buy single article

Instant access to the full article PDF.

USD 39.95

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23
Fig. 24
Fig. 25
Fig. 26
Fig. 27

References

  1. Ksh Newton Singh et al, Eur. Phys. J. C 77, 100 (2017)

    Article  ADS  Google Scholar 

  2. P Mafa Takisa et al, Eur. Phys. J. C 77, 713 (2017)

    Article  ADS  Google Scholar 

  3. D Kileba Matondo, S D Maharaj and S Ray, Eur. Phys. J. C 78, 437 (2018)

    Article  ADS  Google Scholar 

  4. K N Singh, N Pradhan and N Pant, Pramana – J. Phys. 89: 23 (2017)

    Article  ADS  Google Scholar 

  5. P Mafa Takisa and S D Maharaj, Astrophys. Space Sci. 361, 262 (2016)

    Article  ADS  Google Scholar 

  6. D Kileba Matondo et al, Astrophys. Space Sci. 362, 186 (2017)

    Article  ADS  Google Scholar 

  7. R L Bowers and E P T Liang, Astrophys. J. 188, 657 (1917)

    Article  ADS  Google Scholar 

  8. S K Maurya and M Govender Eur. Phys. J. C 77, 347 (2017)

    Article  ADS  Google Scholar 

  9. R I Adam and A Sulaksono, AIP Conf. Proc. 1729, 020010 (2016)

    Article  Google Scholar 

  10. S Ray et al, Phys. Rev. D 68, 084004 (2003)

    Article  ADS  Google Scholar 

  11. C L Rosen, Astrophys. Space Sci. 1, 372 (1968)

    Article  ADS  Google Scholar 

  12. M Gleiser and K Dev, Int. J. Mod. Phys. D 13, 7 (2004)

    Google Scholar 

  13. C W Misner and H S Zapolsky, Phys. Rev. Lett. 12, 22 (1964)

    Article  Google Scholar 

  14. R Garattini and G Mandanici, Eur. Phys. J. C 77, 57 (2017)

    Article  ADS  Google Scholar 

  15. D Shee et al, arXiv:1612.05109 (2017)

  16. F Rahaman et al, Eur. Phys. J. C 75, 564 (2015)

    Article  ADS  Google Scholar 

  17. R Tikekar et al, Grav. Cosmol. 4, 294 (1998)

    ADS  MathSciNet  Google Scholar 

  18. K Komathiraj and S D Maharaj, arXiv:gr-qc/0702102v1 (2007)

  19. S Islam et al, Astrophys. Space Sci. 355, 2205 (2014)

    Google Scholar 

  20. S Thirukkanesh and F C Ragel, Astrophys. Space Sci. 352, 743 (2014)

    Article  ADS  Google Scholar 

  21. R C Tolman, Phys. Rev. 55, 364 (1939)

    Article  ADS  Google Scholar 

  22. M Malaver, Int. J. Mod. Phys. Appl. 2, 1 (2015)

    Google Scholar 

  23. A Einstein, Sitz. Deut. Akad. Wiss. Math. Phys. Berlin 8, 142 (1917)

    Google Scholar 

  24. W de Sitter, Proc. R. Acad. Amst. 19, 1217 (1917)

    Google Scholar 

  25. P Bhar et al, Pramana – J. Phys. 90: 5 (2018)

    Article  ADS  Google Scholar 

  26. M Govender and S Thirukkanesh, Astrophys. Space Sci. 358, 39 (2015)

    Article  ADS  Google Scholar 

  27. S Thirukkanesh, M Govender and D B Lortan, Int. J. Mod. Phys. D 24, 1550002 (2015)

    Article  ADS  Google Scholar 

  28. H Herrera, Phys. Lett. A 165 206, (1992)

    Article  ADS  Google Scholar 

  29. M K Mak et al, Europhys. Lett. 55, 310 (2001)

    Article  ADS  Google Scholar 

  30. W J Kaufmann, Universe (W H Freeman and Company, USA, 1994)

    Google Scholar 

  31. J B Holberg et al, Astron. J. 135, 1225 (2008)

    Article  ADS  Google Scholar 

  32. L James et al, Astrophys. J. 630, L69 (2005)

    Article  Google Scholar 

  33. J L Provencal, Astrophys. J. 494, 759 (1998)

    Article  ADS  Google Scholar 

  34. P Kervella et al, Astron. Astrophys. 488, 2 (2008)

    Article  Google Scholar 

  35. S H Pravdo et al, Astrophys. J. 700, 623 (2009)

    Article  ADS  Google Scholar 

  36. ‘The one hundred nearest star systems’, RECONS. Georgia State University, archived from the original on 2012-05-13, retrieved 2010-06-30

  37. J L Linsky et al, Astrophys. J. 455, 670 (1995)

    Article  ADS  Google Scholar 

  38. J Tomkin and Daniel M Popper, Astron. J. 91, 6 (1986)

    Article  Google Scholar 

  39. M Güde et al, Astron. Astrophys. 403, 155 (2003)

    Article  ADS  Google Scholar 

  40. F Crifo et al, Astron. Astrophys. 320, L29 (1997)

    ADS  Google Scholar 

  41. P Kervella et al, arXiv:astro-ph/0309784 (2003)

  42. L Casagrande et al, Astron. Astrophys. 530, A138 (2011)

    Article  Google Scholar 

  43. J Fernandes et al, Astron. Astrophys. 338, 455 (1998)

    ADS  Google Scholar 

  44. M Stix, The Sun: An introduction (Springer, Berlin, 1991), corrected second print

  45. H Bruntt et al, Mon. Not. R. Astron. Soc. 000, 1 (2010)

    Google Scholar 

  46. J Liebert et al, Astrophys. J. 630, L69 (2005)

    Article  ADS  Google Scholar 

  47. E J Shaya and P Olling Rob, Astrophys. J. 192, 2 (2011)

    Article  ADS  Google Scholar 

  48. A P Hatzes et al, Astron. Astrophys. 457, 335 (2006)

    Article  ADS  Google Scholar 

  49. M Aurière et al, Astron. Astrophys. 504, 231 (2009)

    Article  ADS  Google Scholar 

  50. T Shenar et al, Astrophys. J. 809, 135 (2015)

    Article  ADS  Google Scholar 

  51. P Cruzalébes, Mon. Not. R. Astron. Soc. 434, 437 (2013)

  52. I Ramírez and A C Prieto, Astrophys. J. 743, 135 (2011)

    Article  ADS  Google Scholar 

  53. K Ohnaka Astron. Astrophys. 533, A3 (2013)

    Article  Google Scholar 

  54. J Zorec et al, Astron. Astrophys. 441, 235 (2005)

    Article  ADS  Google Scholar 

  55. Th Kallinger et al, Proc. Int. Astron. Union 848, (2004)

  56. H R Neilson et al, ASP Conf. Ser. 451, 117 (2011)

    ADS  Google Scholar 

  57. M Dolan Michelle et al, Astrophys. J. 819, 7 (2016)

  58. B Arroyo-Torres et al, Astron. Astrophys. 554, A76 (2013)

    Article  Google Scholar 

  59. M Wittkowski et al, Astron. Astrophys. 540, L12 (2012)

    Article  ADS  Google Scholar 

  60. D E Beck et al, Astron. Astrophys. 523, A18 (2010)

    Article  Google Scholar 

  61. S M White et al, Astrophys. J. Suppl. 71, 895 (1989)

    Article  ADS  Google Scholar 

  62. M Zechmeister et al, Astron. Astrophys. 491, 531 (2009)

    Article  ADS  Google Scholar 

Download references

Acknowledgements

SI is thankful to P Tarafdar of S.N. Bose National Centre for Basic Sciences for providing some useful insights in the paper. SD is thankful to his sister Nibedita Datta for useful discussions about the cubic polynomial appearing in the paper and he is also thankful to his colleague Md. A Shaikh for helping him with the plots. TKD acknowledges the support from the Physics and Applied Mathematics Unit, Indian Statistical Institute, Kolkata, India, in the form of a long-term visiting scientist (one-year sabbatical visitor).

Author information

Authors and Affiliations

  1. Department of Physics, Harish-Chandra Research Institute, HBNI, Chhatnag Road, Jhunsi, Allahabad, 211 019, India

    Safiqul Islam, Satadal Datta & Tapas K Das

  2. Physics and Applied Mathematics Unit, Indian Statistical Institute, Kolkata, 700 108, India

    Tapas K Das

Authors
  1. Safiqul Islam
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Satadal Datta
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Tapas K Das
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Safiqul Islam.

Rights and permissions

Reprints and Permissions

About this article

Verify currency and authenticity via CrossMark

Cite this article

Islam, S., Datta, S. & Das, T.K. A parametric model to study the mass–radius relationship of stars. Pramana - J Phys 92, 43 (2019). https://doi.org/10.1007/s12043-018-1704-0

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s12043-018-1704-0

Keywords

  • General relativity
  • relativistic star
  • electric field
  • gravitational potential
  • a–b parameter space
  • stars Hertzprung–Russel diagram

PACS Nos

  • 95.30.Sf
  • 98.80.Jk
  • 98.52.-b