Introduction

The epidemiology of infection has changed over time, reflecting improvements in clinical intervention and the emergence of threats such as antimicrobial resistance. Coronavirus is a specific type of virus that causes respiratory diseases in humans. Corona means “crown” The virus is named after the protein outside the virus. which looks like a crown. The coronavirus, which can cause respiratory illnesses that lead to pneumonia with a mild cold, causes most people to become infected with the coronavirus at any point in their lives. Research is underway to see how COVID19 pneumonia differs from other types of pneumonia. Pneumonia is a lung infection, which inflames the small air sacs in the lungs. They can be difficult to breathe because they are filled with too much liquid and cough. Shortness of breath, fever, cough, chills, malaise and chest pain are among the additional severe symptoms. A person with pneumonia may develop acute respiratory distress syndrome (ARDS), an illness that causes a sudden start of breathing problems. A novel coronavirus causes severe pulmonary inflammation. It harms the cells and tissues that support the air sacs in the lungs. These sacs are where oxygen is processed and sent to the blood. Damage caused by tissue damage is a blockage of the lungs.

A new coronavirus confirmed in Severe Acute Respiratory Syndrome2 (SARSCoV2) occurred in December 2019, causing a new coronavirus disease (COVID19). The Ireroy virus, in which the virus appeared, spread rapidly and was declared a worldwide epidemic. There were over 100 million cases globally as of the end of January 2021, with more than 2 million deaths recorded. To stop the disease from spreading, large-scale testing is needed, however due to a shortage of test kits and a restricted supply, other testing methods are being considered. Chest x-ray (CXR) images have recently been identified to provide vital information concerning COVID19, according to researchers. Intelligent technologies can assist radiologists in detecting COVID 19 from CXR pictures, which is useful in many poor nations with remote sites.

Medical imaging is an essential component of numerous applications in today’s healthcare scenario. Such applications can be found throughout the clinical course of events, not just in the clinical analytic context, but also in the areas of monitoring and radiotherapy procedure, planning and development. The job of clinical imaging has extended past the basic representation and examination of anatomic structures. Recently, fractal dimension technique has been used widely in medical images to detect the fractalness of the object of the study which is a very much common feature extraction methodology to quantify rough texture in medical images. In the proposed proposal the objects of study are very much irregular and hence a fractalness feature of the edge is a good characteristic to extract it [1,2,3].

In general, fast diagnosis of viral infection is required to prevent a pandemic from spreading through a community. Although there are many appropriate standard techniques for virus characterization, they are time-consuming, laborious, and require a skilled expertise to handle. The diagnosis of viral infection, in particular, encompasses the isolation and detection of nucleic acids by collecting specimens (sample was taken) from appropriate sites. For comparison purposes, oral or nasal swab samples, nasopharyngeal or tracheal crude methanol extract, lung tissue, blood, sputum, and faecal are collected to conduct an investigation the pandemic, COVID-19, for effective and fast diagnostic testing, and subsequently for treatment.

and other modulation [4,5,6]. Fractal Dimension (FD) is a popular technique to detect the undefined geometrical structure found in nature. These perplexing items are neglected to examine by old style Euclidean calculation. The idea of FD has broadly applied in numerous regions of use in image preparation. The idea of the FD will work dependently on the hypothesis of self-similitude since it holds structures that are settled with each other [7]. Throughout the most recent years, fractal math was applied broadly in clinical image investigation so as to recognize disease cells in human body in light of the fact that our vascular framework, sensory system, bones, and bosom tissue are so unpredictable and sporadic in design, and furthermore effectively applied in ECG signal, cerebrum imaging for tumor identification, trabeculation examination, and so forth. So as to dissect these unpredictable structures, the greater part of the analysts is receiving the idea of fractal calculation by methods for box tallying strategy [8]. This part presents a review of box tallying and its improved calculations and how they work and their application in the field of clinical picture handling [9].

The rest of the paper is organized as follows. The background study is demonstrated in Section 2. A short literature survey on fractal geometry and box counting method are discussed in Section 3. Section 13 discusses about the experimental datasets used. Section 4 deals with proposed methodologies. Section 5 explains the comparative result analysis of the proposed algorithm. Section 7 concludes the paper by mentioning some possible future research. directions.

Background Study

Theoretical Background of Box Counting Method

Box counting is a data collection approach for studying complicated patterns that involves breaking down a dataset, object, image, or other thing into smaller parts, usually “box”-shaped, then examining the pieces at each lower scale. The theoretical background of the box counting method is discussed here,

Equivalent Definitions of Box Counting Dimension

Definition 1

Let F is assumed as non-empty bounded subset of \(R^{n}\) and let \(N_{\delta }(F)\) represent the smallest no. of sets of diameter at most \(\delta\) which can cover F. F’s upper and lower box counting dimensions are determined as follows:

$$\begin{aligned} \underline{\dim }_{B}F=\underline{\lim }_{\delta \rightarrow 0}\frac{N_{\delta }(F)}{-log \delta } \end{aligned}$$
$$\begin{aligned} \overline{\dim }_{B}F=\overline{\lim }_{\delta \rightarrow 0}\frac{N_{\delta }(F)}{-log \delta } \end{aligned}$$

If these are equal, the common value is referred to as the box dimension of F.

$$\begin{aligned} \dim _{B}F=\lim _{\delta \rightarrow 0}\frac{N_{\delta }(F)}{-log \delta } \end{aligned}$$
Note::

Throughout we shall assume that \(\delta >0\) is significantly small to ensure that \(-\log \delta >0\). We also assume the sets considered are non-empty and bounded to avoid \(\log 0,\log \infty\).

Proposition 1

The lower and upper box dimensions of a subset of \(R^{n}\) are given by

$$\begin{aligned} \underline{\dim }_{B}F=\underline{\lim }_{\delta \rightarrow 0}\frac{N_{\delta }(F)}{-log \delta } \end{aligned}$$
$$\begin{aligned} \overline{\dim }_{B}F=\overline{\lim }_{\delta \rightarrow 0}\frac{N_{\delta }(F)}{-log \delta } \end{aligned}$$

where \(N_{\delta }(F)\) can be thought as any of the following:

  1. i.

    the smallest number of closed balls of radius \(\delta\) that cover F.

  2. ii.

    the smallest number of cubes of side \(\delta\) that cover F

  3. iii.

    the number of \(\delta -\)mesh cubes that intersect F

  4. iv.

    the smallest number of sets of diameter at most \(\delta\) that cover F

  5. v.

    the maximum number of disjoint balls with centres in F of radius delta

Proof

We show the following cases.

  1. (iii),(iv).

    Let us assume the collection of cubes in the \(\delta -\)coordinate mesh of \(R^{n}\), i.e. cubes of the form

    $$\begin{aligned}{}[m_{1}\delta ,(m_{1}+1)\delta ]\times ...\times [m_{n}\delta ,(m_{n}+1)\delta ] \end{aligned}$$

    where \(m_{1},...,m_{n}\) are integers. Let \(N^{\prime }_{\delta }(F)\) be the number of \(\delta -\)mesh cubes that intersect F. They clearly provide a collection of \(N^{\prime }_{\delta }(F)\) sets of diameter \(\delta \sqrt{n}\) that cover F. So,

    $$\begin{aligned} N_{\delta \sqrt{n}}(F)\le N^{\prime }_{\delta }(F) \end{aligned}$$

    On the other hand let \(F_{1},F_{2},...,F_{N_{\delta }(F)}\) be the \(\delta -cover\) (diameter at most \(\delta\))of F. Each \(F_{i}\) (having diameter at most \(\delta\)) is contained in \(3^{n}\) mesh cubes of side \(\delta\)(by selecting a cube containing a point from the set and its neighbouring cubes). Thus \(3^{n} N_{\delta }(F)\) mesh cubes of side \(\delta\), covers all \(F_{i}\) and hence cover F. Tus

    $$\begin{aligned} N^{\prime }_{\delta }(F)(\text {no of mesh cubes of side }\delta \text {that intersects F}) \end{aligned}$$
    $$\begin{aligned} \le \end{aligned}$$
    $$\begin{aligned} 3^{n}N_{\delta }(F)(\text {no of mesh cubes of side }\delta \text { that intersects }\cup _{i=1}^{N_{\delta }(F)} F_{i}\supset F) \end{aligned}$$
  2. (iii),(iv).

    Let \(N^{\prime }_{\delta }(F)\) be the smallest number of arbitrary cubes of side \(\delta\) required to cover F. Then \(N^{\prime }_{\delta }(F)\) number of cubes are sets having \(\delta \sqrt{n}\) that covers F. So,

    $$\begin{aligned} N_{\delta \sqrt{n}}(F)\le N^{\prime }_{\delta }(F) \end{aligned}$$

    Any set of diameters \(\delta\), on the other hand, is contained in a cube of side \(\delta\). \(\delta\). Let \(F_{1},F_{2},...,F_{N_{\delta }(F)}\) be the sets of diameter at most \(\delta\) that covers F. Then we consider cubes of side \(\delta\) say, \(B_{i}\) which covers each \(F_{i}\). So, total number of cubes required, \(N_{\delta }(F)\) to cover F, but \(N^{\prime }_{\delta }(F)\) is the smallest value. Therefore,

    $$\begin{aligned} N^{\prime }_{\delta }(F)\le N_{\delta }(F) \end{aligned}$$
  3. (v),(iv).

    Let \(N^{\prime }_{\delta }(F)\) be the largest number of disjoint balls of radius \(\delta\) with centres in F, and let the balls be \(B_{1},B_{2},...B_{N^{\prime }_{\delta }(F)}\) whose radius is \(\delta\) and centres in F. If \(x\in F\), then x must be within distance \(\delta\) of one of the \(B_{i}\) otherwise the ball of centre x and radius \(\delta\) will not intersect with any one of \(B_{i}\)’s and hence the ball of centre x and radius \(\delta\) can be added to form a larger collection of disjoint balls. Thus any point of F is within \(\delta\) distance from any one of \(B_{i}\)’s and hence any point of F is within \(2\delta\) distance from any one centre of \(B_{i}\)’s. Thus the \(N^{\prime }_{\delta }(F)\) balls concentric with the \(B_{i}\)’ but of radius \(2\delta\)(diameter \(4\delta\)) covers F. Thus we got \(N^{\prime }_{\delta }(F)\) number of sets having diameter \(4\delta\) that covers F, but \(N_{4\delta }(F)\) is the smallest number of sets having diameter at most \(4\delta\) that covers F,so,

    $$\begin{aligned} N_{4\delta }(F)\le N^{\prime }_{\delta }(F) \end{aligned}$$

    Again let \(B_{1},B_{2},...,B_{N^{\prime }_{\delta }(F)}\) be the disjoint balls of radius \(\delta\) with centres in F. Let \(U_{1},U_{2},...,U_{N_{\delta }(F)}\) be the collection of sets of diameter at most \(\delta\) that cover F. Therefore the collection of \(U_{j}\) must cover the centres of \(B_{i}\). Any \(U_{j}\) that covers a centre of one \(B_{i}\) cannot exceed the set \(B_{i}\) as \(B_{i}\) has radius \(\delta\) and diameter of \(U_{j}\) is also \(\delta\). So,each \(B_{i}\) contains at least one \(U_{j}\) inside it. Since all \(B_{i}\) are disjoint, there are at least as many \(U_{j}\) as \(B_{i}\). Hence

    $$\begin{aligned} N^{\prime }_{\delta }(F)\le N_{\delta }(F) \end{aligned}$$
  4. (i),(iv).

    Let \(N^{\prime }_{\delta }(F)\) be the smallest number of closed balls of radius \(\delta\) that cover F, then \(N^{\prime }_{\delta }(F)\) are the sets of diameter \(2\delta\) that cover F. Therefore,

    $$\begin{aligned} N_{2\delta }(F)\le N^{\prime }_{\delta }(F) \end{aligned}$$

    On the other hand any set of diameter at most \(\delta\) is contained in a closed ball of diameter \(\delta\). Let \(F_{1},F_{2},...,F_{N_{\delta }(F)}\) be the sets of diameter at most \(\delta\) that covers F. Then we consider closed balls of radius \(\delta\) say, \(B_{i}\) which covers each \(F_{i}\). So, total number of closed balls required, \(N_{\delta }(F)\) to cover F, but \(N^{\prime }_{\delta }(F)\) is the smallest value. Theref

    $$\begin{aligned} N^{\prime }_{\delta }(F)\le N_{\delta }(F) \end{aligned}$$

  

The most widely used method in the best fitting procedure is undoubtedly BCM [10]. The box counting technique divides the structure space with a d-dimensional fixed-matrix of square boxes of similar size given a fractal structure implanted in a d-dimensional volume.

Fig. 1
figure 1

Displays the box counting technique for the Koch Curve

Full size image

The no. N(r) of no- empty boxes of size r required to cover the fractal structure depends on r (shown in Eq. 1):

$$\begin{aligned} N(r) \equiv r - D \end{aligned}$$
(1)

The box counting method consequently calculates the number N(r)for various estimations of rand plot the log of the number N(r)versus the log of the genuine box sizer. The estimation of the case tallying measurement Dis evaluated from the Richardson’s plot best fitting bend slant (Fig. 1). The BCM applied to the Koch Curve with box size r = 0.4 (a); r = 1 (b); r = 1.4 (c); r= 2 (d)

A few algorithms [7, 8, 11, 12], dependent on the crate tallying strategy, have been created and broadly utilized for FD estimation, as it very well may be applied to sets with or without self-similitude. Be that as it may, in figuring FD with this technique, one either checks or doesn’t tally a container as indicated by whether there are no focuses or a few focuses in the crate. No arrangement is made for weighting the container as per the quantity of focuses having a place with the fractal and inside the present box.

Related Works

Fractal Geometry in Image Analysis

A fractal is represented as a geometrical item described by two major properties: Actually or roughly like a piece of itself, a self-similar object can be persistently divided into pieces, each of which is a reduced scale duplicate of the whole [13]. In addition,a fractal depicts sporadic shapes that cannot be essentially defined by the Euclidian dimension, but the FD must be familiar with extending the dimension definition to these objects. Nonetheless, the FD can take non-integer characteristics, unlike topological dimensions, meaning that the way a fractal set occupies its space is not subjectively and quantitatively the same as how a traditional geometrical set does [14]. Maragos et al. [15] proposed a method for estimation of fractal dimension which considers the adjustment of the cutoff points and different scales that do not show a single FD, but a variety of FD. The sweeping fractal measurement technique can help to partition images with unpredictable items, and has been utilized in various fields [16]. Morphology is a significant technique which help flawless deficient edges or shapes of objects to a limited degree. An important feature of the software is that it is intuitive, i.e. for the fractal dimension estimation, the user may adjust the cutoff points. This makes it really interesting because there are a few instances on different scales that do not show a single FD, but a variety of FD [17].

S. A. Jayasuriya et al. introduced a novel technique of detecting the brain symmetry plane based on fractal analysis [17,18,19]. Valentin et al. tested MR images of healthy livers and livers with colorectal cancer metastases using the concept of the fractal dimension and the Hurst exponent for diagnostic attributes in tomographic imaging. [20]. Assessments of fractal dimensions are considered using the form of box counting. H. Gao et al. proposed a technology in an improved quick fractal image compression coding method [21,22,23,24]. In addition, a new and faster floating box approach is proposed for the lacunarity evaluation, which uses added area tables and Levenberg-Marquardt technique [25,26,27,28]. Although there are several effective standard techniques for virus recognition, they are time-consuming, laborious, and involve a skilled staff to manage. New methods to determine the textural properties of an image and for clinical imaging have recently been supported by the latest development of both texture analysis and advanced computer technology. The potential of texture analysis algorithms to extract analytically important data from clinical images obtained with various imaging modalities, such as magnetic resonance imaging and PET has generated promising findings (MRI) [29, 30].

In this paper [28], it is discussed that the range of various angioarchitectural formations can be measured by Euclidean and fractal-based boundaries in a multi parametric analysis and it is planned to offer substitute biomarkers of malignancy. In this paper [31], a significant perspective for an improved cardiovascular investigation is the precise segmentation of the left ventricle. An efficient approach for completely automated analysis of the LV epicardium and endocardium shapes is introduced in this work.

Authors [32] studied the impact of the difference and morphological filtering in the estimation of the local and associated fractal dimension of retinal pictures. In this paper  [33], the authors discussed that fractal dimension is an arising research area to describe the irregular items found in nature. These articles are difficult to examine by traditional Euclidian geometry. The idea of FD has been broadly applied in numerous directions in picture processing [34]. In this work [35], For the target representation of tumor microvascular finger printing, the authors concentrated on the importance of computational-based morphometrics. In addition, by presenting the “angio-space” definition, which was the tumor space filled by the microvessels, they introduced the fractal dimension as the most accurate computational system ready to give target limits for the microvascular network representation. The fractal measurement D might be determined from numerous points of view on the grounds that Hausdorff-Besicovitch’s definition  [36]. Basirat et al. [37] The fundamental target of this work is to propose a programmed strategy to decide the stone mass FD in Matlab utilizing advanced picture preparing procedures. This strategy quickens examination and lessens human blunder, yet additionally dispenses with the entrance constraint to a stone face. The proposed technique corrects the brightness of an image by using the histogram balance measure and smoothing filters, then uncovering the edges with the Canny edge detection measurement. The computer then computes FD using the box counting method, which is applied at random to the fractured pixels [38]. It is important to determine the fractal measurement of an unpredictably molded applicant portion in order to apply this optimization technique to a fractal textural model [39]. Furthermore, the predicted usefulness of a discrete Gerchberg-Papoulis bandlimited extrapolation calculation for evaluating the fractal measurement of an unpredictably molded competitor fragment is studied [28].

Fig. 2
figure 2

Pictorial view of Sierpinski triangle

Full size image

Figure 2 shows the Sierpinski triangle: starting with a simple introductory setup of units or with a geometric item, the basic seed design is iteratively applied to itself in such a way that the seed configuration is presented as a unit and these units are arranged as symmetrical as the first units in the seed configuration in the new structure.

The objects that are shown in Fig. 2 are self-similar since a piece of the object is like the entire and the fractal dimension can be determined by Eq. 2:

$$\begin{aligned} dim_{box} (S) := \lim _{\epsilon \rightarrow 0} \frac{\log N (\epsilon )}{\log (1/N)} \end{aligned}$$
(2)

where N represents the number of the auto-similar parts where an object can be divided into parts and Sis represents the scaling, that is, the factor required to measure Nauto-similar parts. In Eq. 2, it is shown that the following values are generated for the Koch fractal (shown in Eq. 3) and the Sierpinski triangle(shown in Eq. 4).

$$\begin{aligned} DKoch=log4/log3 \approx 1.26 \end{aligned}$$
(3)
$$\begin{aligned} Sierpinski=log3/log3 \approx 1 \end{aligned}$$
(4)

Mathematically no all inclusive meaning of FD exists and the few meanings of FD may prompt various outcomes for same object. Among the wide assortment of FD definitions that have been presented, the Hausdorff measurement is doubtlessly the most significant and the most broadly used. Such definition can be hypothetically applied to each fractal set however has the problem that it can’t generally be determined by computational strategies.

Infection Analysis of Chest X-ray Image

Researchers compared immune cells from the lungs of COVID-19 pneumonia patients to cells from patients with pneumonia caused by other viruses or bacteria for the study.

COVID-19 begins in numerous small areas of the lungs, whereas other types of pneumonia infect large areas of the lungs quickly. It then employs the lungs’ own immune cells to spread throughout the lungs over a period of days or even weeks. According to the study’s authors, this is similar to how multiple wildfires spread through a forest.

The primary chest radiological characteristics (CXR) of COVID-19 were described and correlated with clinical outcome in a recent study. Patients with a clinical-epidemiological suspicion of COVID-19 infection were included in this retrospective investigation. CXR shows mottled or diffuse reticular nodular opacity and induration, predominately basal peripheral and bilateral for COVID-19. In our experience, the sensitivity of the baseline CXR was 68.1 %. The RALE score can be used as a quantitative measure of the degree of SARSCoV2 pneumonia in the emergency setting and is associated with an increased risk of ICU admission. [40]

Proposed Methodologies

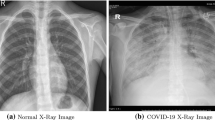
To detect regular dimensions such as circle, rectangle, square several methods are available. To detect any infected area from the images, generated from pathological test detection of undefined geometrical shapes are necessary. For example, from a chest X-ray image if infected areas are to be detected to authenticate any suspected disease, detection of deformed area with good accuracy is one of the challenging work (Figs. 3 and 4).

Fig. 3
figure 3

Example 1 of covid chest X-ray

Full size image
Fig. 4
figure 4

Example 2 of covid chest X-ray

Full size image

This research proposes a technique for producing the FD [41] via BCM in real time. Covid 19 chest X-ray images of healthy livers and livers with colorectal cancer metastases. Since covid 19 chest images and cancerous liver have unknown geometrical shape, fractal analysis is the best approach to calculate the unknown and undefined dimension. The image has been spread with an equivalent number of lattice, and afterward tally what number of boxes of the matrix are covering some portion of the picture. At that point, similar activities that utilize a better network with finer boxes have been carried out. At the end structure of the example has been precisely identified. In this paper, the proposed approach treats the measurement of FD as an estimation problem. Algorithm 0 shows the steps of the proposed method. Figure 5 shows the pictorial representation of the proposed method.

Fig. 5
figure 5

Block diagram of the proposed methodology

Full size image

Results and Discussion

Calculation of Fractal Dimension and Image Analysis

One of the most important concepts in fractal geometry is dimension. Packing, dimension, dimension of box counting, Hausdorff dimension, and dimension of box counting modified are all different definitions of this quantity presently. Because the box counting dimension is simple to create and calculate in mathematics, it has become one of the most extensively used general dimensions. Furthermore, by stating that the measurement findings were equivalent. All of the images in this work were processed with the same crop size and threshold value. Using this strategy, we hypothetically estimated the fractal dimension given in Eq. 5 by using the formula:

$$\begin{aligned} D= \lim _{x\rightarrow 0} \frac{\log {N_{r}}}{\log }{\frac{1}{r}} \end{aligned}$$
(5)

where \(N_{r}\) is the number of squares that include a portion of the considered fractal dimensions and D is the fractal dimension. We created a logarithmic diagram using the generated numbers, with the vertical and horizontal axes were \(\log {N_{r}}\) and\(\log {\frac{1}{r}}\), respectively. The definition of self-similarity, the fractal dimension of mass, the fractal dimension of the spare sphere, the Euclid dimension, the grid style, the empirical approach to fractal decrease, and the fractal dimension box counting are some of the ways for measuring the fractal concept.

The fractal dimension was determined using the self-similar approach from the chest X-ray image which used the box counting approach for the fractal dimension.

For the box counting fractal dimension we suppose that is a non-empty and bounded subset of \(R^{n}\) and we suppose that \(N_{r}(F)\) is the fewest number of collections with a maximum dimension of that can cover. The box counting dimensions (shown in Eq. 6) under and above: if they are equal we say they are equal to the box counting dimension or the box dimension; then, we define

$$\begin{aligned} Dim F = \lim _{x\rightarrow 0} \frac{\log {N_{r}}}{-}\log {\frac{1}{r}} \end{aligned}$$
(6)

Calculation of Hurst Index (H) of the Image

This fractal analysis calculation methodology is illustrated as follows. The fractal dimension explicitly relates to the Hurst exponent, which provides a measure of a surface’s roughness. For example, the fractal dimension has been used to calculate the roughness of coastlines. The relationship between the fractal dimension, D, and the Hurst exponent (shown in Eq. ??), H, is

$$\begin{aligned} D = 2 - H \end{aligned}$$
(7)

There is also a form of self-similarity called statistical self-similarity. For completely uncorrelated noise (white noise), H = 0.5, whereas persistence in the random time series yields H > 0.5 and anti-persistence yields H < 0.5. A persistent time series appears to be smoother. With a larger observational window, there is a greater chance that the window will contain extreme values, and the range R will widen. In the time domain, rescaled range analysis estimates the scaling factor. The whole length T of the time series is divided into \(n = T/t\) observational windows with length t. The rescaled range (lowest to maximum normalized by the standard deviation in that window) is calculated and averaged for each window. A new, longer t is chosen iteratively, and the average rescaled range is computed once more. The scaling exponent H is calculated via nonlinear regression from a number of ranges Ri(T) acquired at various window lengths T. The preceding equation is based on the scaling behaviour of the Brownian time series amplitude and may not apply to every time series.

Figures 6 and 7 show the binary conversion outcome of the original images. Fractional dimensions are assessed by the proposed algorithm. The total number of boxes that touch the black pixel and the scaling variables that produce the dimension are shown in Table 2. In our reliability measure, the value of D in the graph is plotted; the differences between the original line and the line generated by the proposed method are more than 0.9. This means that the dimension of the pneumatic image in this study is reliable.

Fig. 6
figure 6

Example 1 of binary image of covid 19 chest X-ray

Full size image
Fig. 7
figure 7

Example 2 of binary image of covid 19 chest X-ray

Full size image

The result analysis comes with the following findings:

  1. 1.

    Table 1 displays the Scaling factor, number of boxes and corresponding dimension for each scaling factor of Fig. 3.

  2. 2.

    Table 2 depicts the number of boxes and corresponding dimension for each scaling factor of Fig. 4.

  3. 3.

    Figure 8 shows the graphical representation of the dimension of Fig. 3 for each scaling factor in Log/ log graph.

  4. 4.

    Figure 9 shows the graphical representation of the dimension of Fig. 4 for each scaling factor in Log/ log graph.

Table 1 Scaling factor, number of boxes and corresponding dimension for each scaling factor of Fig. 3
Full size table
Table 2 Scaling factor, number of boxes and corresponding dimension for each scaling factor of Fig. 4
Full size table

After observing the pattern of graph it can be determined that it generates a straight line parallel to X axis which validates the theoretical definition of box counting method. By the definition of box counting we know that

$$\begin{aligned} Dimension, D = \frac{log(number of boxes)}{log(scaling factor)} \end{aligned}$$
(8)

Now, if number of boxes considered = x and scaling factor = y. Then Eq. 2 can be represented in y= mx form, which is a straight line parallel to x axis.

In our work, if the dimension values are plotted for each scaling factor in a log/log graph for both image 1 and image 2 it follows the pattern of y=mx (straight line parallel to x axis) which is shown in graph 1 and graph 2 respectively. Hence it can be concluded that the experimental result validates the theoretical definition of box counting.

The accuracy of the experimental result can be calculated by the amount deviation from a pure straight line from that particular point. According to the theoretical definition the more accurate result we get by placing more finer grid in the image. For image 1 with size 222 X 222 when 222 grids are placed, the dimension is 1.47 and for image 2 with size 204x204 when place 204 grids are placed the dimension is 1.69.

Fig. 8
figure 8

Graphical representation of the dimension

Full size image
Fig. 9
figure 9

Graphical representation of the dimension

Full size image

Apart from chest X-Ray in this work, we have also considered sample dataset used in [22] of HLT and LTCMCC for comparative analysis of the proposed method with the state of the method. Table 3 display the comparative analysis of the said method. Considering different window sizes and different sections of the image, the experiments have been performed.

Table 3 Comparative analysis of the proposed method and other methods
Full size table

To identify the appropriate size of the researched area, images of liver tissue were analysed in three parts using frames of varied sizes. In Table 3 we explain the result of the comparison analysis of the BCM and Hurst exponent for all the six different sizes of the image. In Sections 1 and 2 our proposed approach gives us better Hurst exponent value than state-of-the-art approach. In Section 3 for 110x130 the Hurst exponent value is better in state-of-the-art approach whereas we got the Hurst exponent value 0.6 which is greater than 0.5.

The proposed method gives better result compared to the other method because of mainly two reasons:

  1. 1.

    Due to binarization of the image the ROI is clearly visible.

  2. 2.

    Since the numbers of boxes are more than the other method. We assume 264 number of boxes whereas other method considers 12 boxes. The more we increase the number of boxes more accurate result we get.

Performance Analysis

The performance is an important factor of any dimension detection algorithm. An algorithm provides high accuracy but also has high execution time and has no practical use. In ideal case, an algorithm should provide high accuracy for finding the dimension, low time complexity and also should be light weighted so that it can be executed in low precision devices. Our proposed algorithm is computed in the machine with following software and hardware specifications: Windows 10 (64 bit) operating system is chosen with Matlab R2022a. Intel(R) Core(TM) i3-6006U CPU @ 2.00GHz 1.99 GHz with RAM of 8 GB Memory. We have computed the execution time which is illustrated in Table 4 for various sizes of input images. The time complexity is also plotted in a line graph for better visualization and captured in Fig. 10. It can be seen that the average speed of the images having dimension 56\(\times\)56 is approximately 0.5 min. For the images having sizes 112\(\times\)112, 256\(\times\)256, 512\(\times\)512 and 1024\(\times\)1024 are approximately 0.6 and 2.3 min respectively.

Table 4 Execution time analysis for different sizes of the input image
Full size table
Fig. 10
figure 10

Performance analysis of the images w.r.t size

Full size image

Conclusions

In this paper, a novel methodology of dimension detection of medical images has been proposed based on the concept of box counting approach to evaluate the fractal dimension in unpredictable ROI-s. The findings appear to be significant for diagnostic purposes, according to the findings. The proposed approach works efficiently on grey scale or binary images only. The proposed approach cannot perform well on RGB images. Additionally, in future, this dimension detection technique can be implemented for larger dataset to make the approach more scalable. Also, the detection of dimension of an object with various pixel intensity can be focused along with dimension detection problems for overlapping objects in an image.