1 Introduction

Ti6Al4V alloy is the workhorse of several industries, such as biomedical, aerospace, chemical, and marine, due to its high strength-to-weight ratio and corrosion resistance [1]. However, joining this material poses numerous challenges as it is easily oxidized at high temperatures and requires an inert environment [2]. Fusion welding techniques such as tungsten inert gas (TIG) welding and laser welding (LW) have been the most common welding technologies as they are economically feasible and offer high joint integrity [3]. However, achieving optimum parameters that will give desired physical and mechanical properties is not easily achieved without several trial welds.

Some challenges in welding thin sheet metals include maintaining a stable keyhole during welding, as deep penetration is required, and good dilution of the melt pool is important to achieve a sound weld. Also, a high laser beam intensity causes rapid evaporation of the melt pool. In addressing this challenge, the ratio of laser beam diameter to welding speed, known as the welding characteristic time, was proposed by Guo et al. [4]. The higher the ratio, the higher the penetration depth; this was further confirmed by Song et al. [5], as their study also indicated that the laser beam shape affects the weld width and penetration depth. They further confirmed that a spot wobble laser beam achieves higher mechanical strength over the donut-shaped laser beam during high-power laser welding. Furthermore, warping and distortion are also major challenges when it comes to thin sheet welding and achieving a good curvature, as they affect production precision. Welding speed has been reported to have a significant effect on the deformation of a material after welding; other parameters include current and welding voltage [6].

Several reports on the effects of welding parameters have been reported to affect welded metal’s bead geometry and mechanical properties. The effect of welding parameters on weld geometry was observed by Akman et al. [7], who reported that the weld penetration and weld bead can be controlled through power input [8]. An increase in power input increases the temperature within the material, thereby increasing the evaporative tendency of the molten pool, resulting in undercut or crater formation within the material’s surface [9,10,11]. Furthermore, low heat input is reported to result in V-shaped bead geometry, while H-shaped results from high heat input [12].

Welding speed plays an important role in the geometry of weld beads. With increased welding speed and heat input, the weld pool becomes more elongated, changing from an elliptical form to a teardrop shape [13]. In a study by Wang et al. [14], keyhole size is reported to be affected mainly by the welding speed and laser power. A decreased welding speed can result in a less symmetrical keyhole profile [15]. Furthermore, by reducing welding speed, there is a wider bead as more power density is used in the material [16, 17]. Another critical parameter is the defocusing distance, which is the distance between the focal plane of the laser beam and the workpiece being welded. It greatly affects the bead geometry, depth penetration, and heat distribution during welding [18]. In a study by Caizzo et al. [19], the bead crown and root increased with defocusing distance. Positive defocusing distance results in less porosity, whereas the negative defocusing distance has a good penetration depth but has been associated with porosities [20].

Heat input has also been identified to affect the microstructure and mechanical properties of Ti6Al4V alloy; high heat input has resulted in the formation of martensitic microstructure, which increases hardness [21, 22]. To have an acceptable weld that meets industrial standards, the weld bead must be porosity and crack-free; the right parameter combination must be used to achieve this. Different predicting tools have been deployed in optimizing welding parameters, some of which are the artificial neural network (ANN) [9, 23], response surface methodology (RSM) [19], Taguchi [24], finite element method (FEM) [10] and others. However, there is still a need to optimize welding parameters to achieve multiple physical and mechanical properties from the welded material.

The Grey relational analysis (GRA) is an optimization tool that is an effective approach to optimizing multiple objectives concurrently. It transforms multiple performance characteristics into a single grey relational grade, thereby enabling a comprehensive evaluation of responses. Therefore, this study uses the Taguchi-Grey relational analysis to optimize the welding parameters of laser welded Ti6Al4V alloy to achieve an optimum bead width, height, and hardness within the fusion zone (FZ).

2 Materials and methods

2.1 Experimental technique

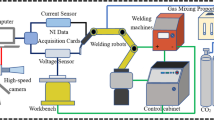
Sheets of Ti6Al4V alloy with dimensions of 100 × 60 × 3 mm and chemical composition of 4% V, 0.15% Fe, 0.13% O, 0.03% C, and 6.1% Al, with the remaining being titanium, were joined in the butt configuration using the 3 kW CW YLS-2000-TR ytterbium laser system. Before welding, the faying sides were cleaned with acetone to remove impurities before joining autogenously. Argon gas at a flow rate of 15 L/min was used as the shielding gas, and the experimental setup is shown in Fig. 1. Welding parameters were designed using the L9 (32) Taguchi orthogonal design of experiment, as shown in Table 1.

Table 1 Experimental design
Full size table
Fig. 1
figure 1

Experimental setup

Full size image

The welded samples were prepared for microstructural analysis by cutting them into 25 × 10 × 3 mm sizes. They were mounted on thermoset resins, and grinding was done using SiC papers ranging from 320 to 1200 microns and was polished till the mirror surface was achieved. The samples were etched using the Kroll’s reagent, and the weld profile was captured with the Olympus SZX16 macroscope. The bead width and height were measured using the Olympus Stream Essentials software, as shown in Fig. 2, where W is the bead width and H is the bead height. The microhardness was measured using the Indentec digital microhardness tester at a load of 4.9 N and a dwell period of 15 s. Fig. 3 shows the laser welded Ti6Al4V alloy sheets.

Fig. 2
figure 2

Schematics of the weld bead

Full size image
Fig. 3
figure 3

Welded samples

Full size image

2.2 Optimization technique

The Taguchi-Grey relational analysis is carried out following the simple steps highlighted as follows:

2.2.1 Taguchi design

The L9 (32) Taguchi design has been adopted to optimize the welding parameters. Taguchi is a robust tool that reduces the sensitivity of responses to have variability without eliminating the causes of the variability [25]. The technique identifies the factors not within the manager’s control as noise factors and those within the control as signal factors. The Taguchi technique adopts three signal-to-noise factors: the nominal is best, as shown in Eq. 1, smaller the better; Eq. 2 and larger the better, Eq. 3 [26]. In this study, “the larger is better” is adopted to optimize the hardness, as higher hardness in Ti6Al4V alloy results in lower abrasive wear and is suitable for high load-bearing components [27]. However, nominal is better adopted for the bead geometry as there are no exact accepted sizes for weld beads. Nonetheless, having a good weld penetration and a narrow bead width is important.

Nominal is better signal-to-noise ratio:

$$\eta = 10\log \frac{1}{n}\sum\nolimits_{i = 1}^n {\frac{{{\mu ^2}}}{{{\sigma ^2}}}}$$
(1)

Where,

$$\mu = \frac{{{y_1} + {y_2} + {y_3} + \ldots \ldots + {y_n}}}{n}$$
$$\sigma = \frac{{\sum {{{\left( {{{\text{y}}_{\text{1}}}{\text{ - }}\overline {\text{y}} } \right)}^{\text{2}}}} }}{{{\text{n - 1}}}}$$

The smaller the better signal-noise ratio:

$$\eta = - 10\log {1 \over n}\sum\nolimits_{i = 1}^n {{y_1}^2}$$
(2)

Larger is better signal-to-noise ratio:

$$\eta = {\text{ - 10log}}\frac{{\text{1}}}{{\text{n}}}\sum\nolimits_{{\text{i = 1}}}^{\text{n}} {\frac{1}{{{y_i}^2}}}$$
(3)

Where ƞ is the signal-to-noise ratio, n is the number of replicas, yi is the observed response, µ is the mean of the signal-to-noise ratio, and σ is the standard deviation.

2.2.2 Grey relational analysis

2.2.2.1 Normalization

The grey relational analysis theory was conceived in the 1980s by Julong Deng [28]. The technique transforms responses into Grey relational grade (GRG) and combines multiple responses into one response [28]. In this study, three responses, the bead width, height, and hardness, were transformed into one response. Normalization is the first step in carrying out Grey relational analysis, which changes the data between 0 and 1. Equation 4 is used for the dataset normalization for the higher, the better, and Eq. 5 is used for the smaller, the better. However, if the demanded value is within the analyzed value, the normalization can be done using Eq. 6 [29].

$${x_i}{\mkern 1mu} \left( k \right) = \frac{{{x_i}^0\left( k \right) - \min {\mkern 1mu} {x_i}^0\left( k \right)}}{{\max {\mkern 1mu} {x_i}^0\left( k \right) - \min {\mkern 1mu} {x_i}^0\left( k \right)}}$$
(4)
$${x_i}{\mkern 1mu} \left( k \right) = \frac{{\max {\mkern 1mu} {x_i}^0\left( k \right) - {x_i}^0\left( k \right)}}{{\max {\mkern 1mu} {x_i}^0\left( k \right) - \min {\mkern 1mu} {x_i}^0\left( k \right)}}$$
(5)
$${x_i}\,\left( k \right) = 1\, - \frac{{\left| {{x_i}^0\left( k \right) - {x^0}} \right|}}{{\max \left[ {\max \,{x_i}^0\left( k \right) - {x^0},{x^0} - \min \,{x_i}^0\left( k \right)} \right]}}$$
(6)

Where x*i(k) is the sequence after data processing, x0i(k)is the original sequence of the dataset, and min x0i(k) is the smallest value of x0i(k). Max x0i(k) is the maximum value of x0i(k), and x0 is the assigned value in the data sequence.

2.2.2.2 Deviation sequence calculation

This is the absolute difference between the maximum value obtained after normalization and the corresponding reference sequence. It is given as:

$${\Delta _{ij}}=\left| {{Y_{ij\hbox{max} }} - {Y_{ij}}} \right|$$
(7)

Where \({\Delta _{ij}}\)is the deviation sequence, the maximum value obtained after minimization, and the corresponding reference sequence.

2.2.2.3 Grey relational coefficient (GRC)

The Grey relational coefficient is calculated using Eq. 8.

$$GR{C_i}\left( k \right)=\frac{{{{\hbox{min} }_i}\left| {{x_i}^{0} - {x_i}\left( k \right)} \right|+\xi {{\hbox{max} }_i}\left| {{x_i}^{0} - {x_i}\left( k \right)} \right|}}{{\left| {{x_i}^{0} - {x_i}\left( k \right)} \right|+\xi {{\hbox{max} }_i}\left| {{x_i}^{0} - {x_i}\left( k \right)} \right|}}$$
(8)

Where \(GR{C_i}\left( k \right)\)is the GRC for the response k, \({x_i}^{0}\)is the values of the experiment, and \(\xi\)is the distinctive coefficient over the range 0<\(\xi\)<1. This study adopts 0.5 as it is considered stable [28].

2.2.2.4 Grey relational grade (GRG)

The final stage is grading the response, achieved using Eq. 9.

$$GR{G_i}=\frac{1}{n}\sum\limits_{{i=1}}^{n} {GR{C_i}\left( k \right)}$$
(9)

Where \(GR{G_i}\)is the Grey relational grade for the responses, and n is the number of responses?

2.2.3 Analysis of variance (ANOVA)

ANOVA is a statistical tool used to evaluate each operating parameter’s influence on the variation of responses. Minitab 2021 version is employed to carry out ANOVA in this study.

3 Results and discussion

3.1 Experimental results

Fig. 4 shows the microstructure of the welded samples; each micrograph shows an hourglass shape at the fusion zone, indicating a full weld penetration. Table 2 shows that increasing laser power increases the bead width, which could be attributed to an increase in the melt pool. However, due to the high heat input, the weld pool’s rapid evaporation results in an undercut in the bead geometry.

Table 2 Experimental results
Full size table

Furthermore, the microstructure in Fig. 5 shows a typical microstructure of the weld at various zones. The base metal (BM) Fig. 5a comprises the equiaxed α and β phases [30]. Other phases have been observed to have undergone phase transformation as heat applied has affected them. The heat affected zone far from the fusion zone (FHAZ) Fig. 5b is made of the blocky α and β phases, with larger grain sizes than the BM, as this zone is affected by temperature lower than the β transus temperature of Ti6Al4V alloy, which has been reported to be around 995°C [31]. Furthermore, the heat affected zone near the fusion zone (NHAZ) Fig. 5c is observed to have attained temperature above the β transus temperature but below the melting temperature of the metal. The zone predominantly consists of the α acicular and the transformed β phase, which is fine due to the increased β grain growth. Fig. 5d is the fusion zone that has attained the melting temperature of the metal and is made up of the needle-like α’ martensitic microstructure, which results from the rapid cooling of the phase at about 410 °C/s [32]. This microstructure is responsible for high hardness within the zone [33].

Fig. 4
figure 4

Microstructure of welded samples

Full size image
Fig. 5
figure 5

Microstructure of laser welded Ti6Al4V at (a) base metal (BM), (b) heat affected zone far from the fusion zone (FHAZ), (c) heat affected zone near fusion zone (NHAZ), (d) fusion zone (FZ)

Full size image

3.2 Microhardness evolution

Figure 6a shows the microhardness indentations made across the weld with three replicas. Each indentation was made at an interval of 1 mm. Fig. 6b shows the hardness distribution within the different zones of the material. The average hardness of the base metal is 351.2 ± 4.1 HV. Hardness increases towards the fusion zone due to different grain structures within the phases. The highest hardness was observed within the fusion zone with an average hardness of 400.2 ± 2.4 HV, which can be observed in the trends presented in Table 2. The average hardness value of the fusion zone is 400.2, which is 49 HV higher than the base metal hardness (351.2 HV) and 19.4 HV higher than the heat affected zone hardness (380.8 HV). These results are similar to those of Junaid et al. [27], who worked on laser welding of titanium alloy. Furthermore, the α martensitic and acicular microstructure within the heat affected and fusion zones have been attributed to the high hardness. The evolution of the microstructure in the FZ and HAZ is due to the occurrence of rapid cooling at the weld pool and heat affected zone [32].

Fig. 6
figure 6

Microhardness profile showing (a) diamond indentation points and (b) surface plot of the laser welded Ti6Al4V alloy at different weld zones

Full size image

3.3 Taguchi optimization analysis

Table 3 shows the signal-to-noise ratio of the responses, and it is observed that the maximum bead width, bead length, and hardness value shown in Fig. 7 are laser power at level 2 (2.9 kW), welding speed at level 2 (2.4 m/min) also for the bead width optimization. Also, for the bead length optimization, laser power is at level 3 (3 kW), and welding speed is at level 1 (2.2 m/min). Furthermore, hardness is optimized at level 1 (2.8 kW) laser power and level 3 (2.6 m/min) welding speed. These results further ascertain that the welding parameters, such as laser power and welding speed, do not significantly affect the bead width. However, literature has reported that defocusing distance significantly affects the bead width [17]. Furthermore, the penetration depth is affected by laser power increase, resulting in more heat input and increased weld pool. Hardness is also affected by heat input as the formation of the martensitic microstructure requires rapid cooling from the melting temperature. However, the Grey relational analysis will be done to have a general optimization common to all the responses.

Table 3 Signal to noise ratio of the responses
Full size table
Fig. 7
figure 7

Mains effect plot for (a) means of bead width against the welding parameters, (b) means of beath length against the welding parameters, and (c) signal-to-noise ratio of hardness against the welding parameters

Full size image

3.4 Taguchi-Grey relational analysis

The Grey relational analysis uses the steps highlighted in Sect. 2. The normalized values are given in Table 3, deviation sequence, and the Grey relational coefficient are presented in Table 4. Table 5 gives the ranking of the responses which have been grouped. The ranking presented in Table 5 shows that the sample L31 welded with laser power of 2.8 kW and 2.2 m/min welding speed ranks first. The Grey relational grades (GRG) were then subjected to Taguchi optimization and parameters with 3 kW laser power and 2.2 m/min welding speed as the optimum parameter to achieve the best bead length, bead width, and hardness as shown in Fig. 8. Furthermore, Table 6 shows the response of the GRG, and it gives the information that the welding speed > laser power to achieve an optimal welding parameter.

Table 4 Deviation sequence and the Grey relational coefficient of the responses
Full size table
Table 5 Grey relational grading and ranking of the responses
Full size table
Fig. 8
figure 8

Mains effect plot for the signal-to-noise ratio of the Grey relational grade

Full size image
Table 6 Response table for signal-to-noise ratios of GRG
Full size table

3.5 Analysis of variance (ANOVA) results

The ANOVA results are presented in Table 7. It is used to determine the statistical significance of each operating parameter, i.e., the impact level of each operating parameter on the output or resulting parameters. The confidence interval is 95% for all ANOVA results from Table 7. It is observed that neither of the two process parameters significantly impacted the bead width. Further analysis considering the effect of the input parameter interactions on bead width is shown in Table 8. The results show no significant process parameter impact on the bead width. The results further confirm the results of the Taguchi analysis, which shows that the laser power and welding speed have little or no effect on the bead width in this study. The interaction of the welding speed had the highest contribution of 46.28%. However, the P-value is still insignificant at a 95% confidence interval. The model has an 81.33% R squared value.

Table 7 ANOVA results of bead width
Full size table
Table 8 ANOVA results of bead width with parameter interactions
Full size table

Similar to the ANOVA results of the bead width, the bead length also showed identical characteristics, as the input parameters show no significant effect on the bead length, as shown in Table 9. Further ANOVA analysis shown in Table 10, which incorporates interactions between parameters, showed that even though the welding speed contributed about 38.43% to the significance of the model, the P-value is still higher than 0.05 at a 95% confidence interval, so also is the interaction of the welding speed which has a P-value of 0.083. The results signified that welding speed impacts the weld penetration of the material.

Table 9 ANOVA results of bead length
Full size table
Table 10 ANOVA results of bead length with parameter interactions
Full size table

Table 11. shows the ANOVA results of the hardness of the welded material. However, the ANOVA result did not give a good level of significance. Further analysis in Table 12 shows that the interaction between laser power and welding speed is significant and impacts the hardness outcome.

Table 11 ANOVA results of hardness
Full size table
Table 12 ANOVA results of hardness with parameter interactions
Full size table

To have the significance of each parameter using grey relational grade results shows that the interaction of laser power and welding speed posses a significant effect on the hardness and bead geometry of laser welded Ti6Al4V alloy sheets in this study.

Table 13 ANOVA results of the Grey relational grade with parameter interactions
Full size table

4 Conclusions

In this study, 3 mm thick Ti6Al4V alloy sheets were joined in the butt configuration using laser welding. The Taguchi-Grey relational analysis optimized the laser power and welding speed to achieve optimum bead width, length, and hardness. It is concluded that.

  1. 1.

    The laser power significantly impacts the bead length. That higher heat input increases the depth of penetration in the weld. At the same time, the welding parameters have little or no effect on the bead width, as the defocusing distance is the primary factor determining the width of welding beads in laser welding.

  2. 2.

    The micrographs show that the welding parameters result in full weld penetration.

  3. 3.

    The microstructure of the welds consists of α martensitic microstructure at the fusion zone and the heat affected zone near the fusion zone. This microstructure is responsible for the high hardness within the zones.

  4. 4.

    The welding speed and laser power significantly affect the welded material’s hardness.

  5. 5.

    ANOVA results confirmed the results of the Taguchi analysis at a 95% confidence level, with the interaction of laser power and welding speed contributing 40.65% to the hardness and bead geometry of the laser welded Ti6Al4V sheet.

  6. 6.

    The optimal process parameter was determined to be 3 kW laser power and 2.2 m/min welding speed.