1 Introduction

The design of AS-FC requires to consider particular precautions for an optimal performance under operation. Standards for dimensioning and tolerancing [1, 2] consider non-rigid parts which deform substantially from their manufactured condition and provide procedures for the geometrical specifications of these parts, which generally apply in the restrained assembled condition. The behaviour of AS-FC is complex and their design specifications can be improved only through effective computational methodologies that study the interaction among the parts [3,4,5]. This is confirmed by the fact that the dynamic characterization of many of these assemblies, where different parts interact with each other, occurs almost exclusively by means of experimental testing [6,7,8].

Frequent is also the usage of AS-FC to dampen or absorb transient mechanical vibrations of components such as gears, supports, transmissions, chain drives, linkages, bearings, brakes, fasteners, sensors, cables, etc. in different mechanical systems (actuators, engines, transmission and transport systems, manufacturing systems, etc.) [9]. This is important since vibrations are a common source of undesirable effects such as wear, fatigue, noise, etc. in industrial, military, naval, and aerospace applications.

Nowadays another widely used category of AS-FC is that of compliant mechanisms. They are flexible structures that gain mobility from deflection of flexible components rather than kinematic pairs [10]. In particular, in the field of robotics, it’s possible to find many recent studies concerning design methods [11] and topological optimization of compliant mechanisms [12].

Mainly two different types of AS-FC can be distinguished, namely extended assembled systems made up of several parts all having comparable stiffness (aeronautical, automotive and robotic structures) [13] and assembled systems, in which few parts are much less rigid than others (supports, dampers, isolators, etc.) [14].

For both of these types the design is not limited to its geometric dimensioning and modelling; interference and contact problem require the utilization of proper computational approaches for the analysis of assembly functional behaviour. Several research studies demonstrated the need to consider tolerances in the calculation and simulation stages of the AS-FC development [15, 16]. In fact, the correct modelling of AS-FC requires consideration of geometrical and dimensional manufacturing inaccuracies as well as the deformations caused by external loads. The above defects subsequently affect the functional requirement and the efficiency of the AS-FC [17].

In this work, the AS-FC with parts much less rigid than others were specifically considered for the study of the influence that the shape and the size of the flexible components have on the assembled system performance. The analysis was carried out though a proper combination of computational methodologies whereby a mesh morphing (MM) formulation in non-linear numerical FEA, including contact problems and flow interaction was applied. In particular, through the evaluation of specific energy absorption (SEA), the proposed computational method allowed to optimize the shape and size of flexible components. The system's ability to absorb energy was maximized respecting the correct values of ISO-ASME tolerances specification with which flexible components are assembled in the system directly in the FEA environment.

It is observable, in fact, that usually the deformation of flexible components in assembled mechanical systems occurs within a viscous fluid in order to increase its energy absorption performance [18]. To address these challenges the method proposed herein allows, through an appropriate interactively integration of the CAE tools (MM, non-linear structural analysis and flow interaction), the optimization of the shape and size of flexible components.

The main original contribution of the proposed approach is that shape and size of flexible component can be analysed and optimized by directly modifying the calculation grid in FE simulation environment without the CAD model undergoing any modification. This allows to quickly evaluate the influence of shape and size changes on AS-FC performance also taking into account assigned tolerances.

For validation, the forecasting capability of the method is presented and verified for the case study of an automotive crash shock absorber.

The paper is organized as follows: in Sect. 2 materials and methods of the proposed methodology are described; Sect. 3 illustrates the application and validation of the method to a crash shock absorber for car bumpers; in Sect. 4 the main results obtained with the methodology are discussed; finally, in Sect. 5, conclusion with closing remarks and future research developments are reported.

2 Materials and methods

The computational optimization of shape and size of flexible components in assembled mechanical systems traditionally occurs through iterative processes in which geometric modifications are carried out at the first steps. In general, no single absolute best solution for geometry optimization of flexible components exists. Often the best solution is chosen as a compromise by experimentally testing different prototypes.

In the present approach, the RBF, a class of interpolation mathematical functions, was used directly in the FEA environment to perform shape and size optimization of flexible components via MM. Using RBF-MM on the discretized domain in CAE applications, it was possible to apply predefined displacements to a set of generated points, which are called source points, directly to the computational model in FE environment. In this way RBF-MM formulation allows to define, directly in the FE environment, a parametric model of flexible parts. In Fig. 1a, the workflow of the proposed methodology is schematized, while Fig. 1b shows the traditional method based on iterative processes in which geometric parametrization and modifications are the basis of the process.

Fig. 1
figure 1

Comparison between: a the proposed methodology and b the traditional geometric optimization approach

Full size image

Through the formulation illustrated in the following paragraph RBF-MM allows to carry out the geometric modifications of shape and size of flexible components in non-linear numerical FEA, including non-linear sliding contacts and flow interaction.

2.1 Parametrization with RBF MM

The flexible parts of assembled systems were geometrically parameterized with the desired tolerances using an appropriate number of source points. Through source points, the geometric parametrization based on RBF-MM implemented shape modifiers, amplified by parameters, directly on the computational domain. New geometric configurations resulted from the displacement of a set of mesh regions (walls, boundaries or discrete points within the volume) through the use of algorithms, based on RBFs, which smoothly propagated the imposed displacement to the surrounding volume.

The number and position of source points were established in such a way to ensure the functionality of the system, in relation to the established tolerances [19,20,21].

Evaluating the accuracy derived by morphing the source points were properly incremented introducing further driving points in the areas where unwanted deformation between the morphed surface and theoretic surfaces of the flexible component had maximum values.

The surface of deformable parts was discretized by triangular membrane elements; their structural deformation calculation, according to the method of Arcaro [22, 23], assumed homogeneous and orthotropic linear elastic material. Figure 2 shows, as an example, the choice and the localization of the source points related to the study of a fillet in the edge of a parallelepiped.

Fig. 2
figure 2

Parametrization of an edge fillet of a cube with RBF MM

Full size image

The solid straight parallelepiped in Fig. 2a was meshed with tetrahedral elements. A set of source points, equally spaced each other, was defined on a box shaped bounding volume in order to limit the space of the MM action (Fig. 2b). The moving points of parallelepiped located on the part surface showed the domain of the RBF setup (Fig. 2c, d). The limiting source points are marked in red while the moving centres, belonging to the part, are highlighted in green (Fig. 2e, f).

A parametric radius allowed to parameterize the limiting source points and to use the different geometric models obtained in finite element simulations. The boundary conditions fixed then the min and max values of the radius.

A NURBS surface obtained through an extrusion with a circular profile with a radius equal to the value of the parameter radius allowed, in this example, to evaluate the geometric precision of the morphing performed (Fig. 2g).

Figure 2h, i show the final meshed model and the solid model respectively.

Parametrization with RBF MM was employed in literature to obtain shape-based optimization [24], but its use was recently also explored for advanced studies, such as steady [25] and unsteady fluid structure interaction problems, evolutive shape-based optimizations [26, 27].

The advantages of the proposed approach can be so synthesized: there is no need to regenerate the grid; the robustness of the procedure is preserved; it has the capability to support different mesh types thanks to its meshless nature and the high parallelizable smoothing process. The morphing action integrated in a solver updating the computational domain interactively during the progress of the computation can be executed in RBF Morph across three steps: (1) setup: it consists of the manual definition of the morphing targets, i.e. the portions of the FEA mesh that will be updated, and morphing sources, i.e. the portions of the FEA mesh controlled, and the definition of the required movements (design parameters) of the points driving the shape deformation; (2) fitting: the solution of RBF system obtained by collecting the morphing sources; (3) smoothing: it is obtained by propagating the displacement prescribed on sources to the volume mesh target.

2.2 RBF MM theory

The mathematical solution of the RBF problem consists in calculating the coefficients of a linear system of order equal to that of the number of source points [28, 29]. The displacement of an arbitrary node of the grid is imposed as the sum of the radial contributions of each source node. In this way, the morphing of the mesh can be applied quickly while keeping the grid topology unchanged in terms of total number and type of elements.

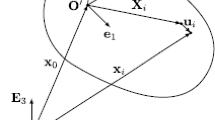
The solution is unique with compatibility for rigid motions when the RBF interpolant is composed by a radial function containing the RBF φ and a multivariate polynomial corrector vector h of order m –1, where m is the order of φ. If N is the total number of source points, the RBF interpolant is:

$$ s\left( x \right) = \mathop \sum \limits_{i = 1}^{N} {\upgamma }_{i} \varphi \left( {\left\| {x - x_{i} } \right\|} \right) + h\left( x \right) $$
(1)

where x is the vector indicating the position of a generic node of the surface and/or volume mesh xk, is the ith source node position vector and \(\Vert \bullet \Vert \) is the Euclidean norm.

The RBF fitting solution is possible when the RBF coefficients vector γi and the weights of the polynomial corrector vector βi are found so that, at source points, the interpolant function has the specified (known) values of displacement gi, whilst the polynomial terms give a null contribution, namely the following relations are simultaneously verified:

$$ s\left( {x_{si} } \right) = g_{si} , 1 \le i \le N $$
(2)
$$ \mathop \sum \limits_{i = 1}^{N} \gamma_{i} p\left( {x_{si} } \right) = 0 $$
(3)

for all polynomials q with a degree less than or equal to that of polynomial h. A unique RBF interpolant exists if the RBF is conditionally positive definite. Moreover, if the order is less than or equal to 2, a linear polynomial applies:

$$ h\left( x \right) = \beta_{0} + \beta_{1} x + \beta_{2} y + \beta_{3} z $$
(4)

allowing for rigid body translations recover. In this case, the interpolant has the form:

$$ s\left( x \right) = \mathop \sum \limits_{i = 1}^{N} \gamma_{i} \varphi \left( {\left\| {{\varvec{x}} - {\varvec{x}}_{ki} } \right\|} \right) + \beta_{0} + \beta_{1} x + \beta_{2} y + \beta_{3} z{ } $$
(5)

and \({\gamma }_{i}\) and \({\beta }_{\mathrm{i}}\) values are obtained by this solution of the system

$$ \left( {\begin{array}{*{20}c} M & {P_{s} } \\ {P_{s}^{T} } & 0 \\ \end{array} } \right)\left( {\begin{array}{*{20}c} \gamma \\ \beta \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {g_{s} } \\ 0 \\ \end{array} } \right) $$
(6)

where U is the interpolation matrix whose elements are derived by calculating all the radial interactions between source points as follows:

$$ M_{ij} = \varphi \left( {\left\| {x_{si} - x_{sj} } \right\|} \right),1 \le i \le N,1 \le j \le N $$
(7)

and P is a constraint matrix that arises balancing the polynomial contribution:

$$ P_{s} = \left( {\begin{array}{*{20}c} 1 & {x_{s1} } & {y_{s1} } & {z_{s1} } \\ 1 & {x_{s2} } & {y_{s2} } & {z_{s2} } \\ \vdots & \vdots & \vdots & \vdots \\ 1 & {x_{sN} } & {y_{sN} } & {z_{sN} } \\ \end{array} } \right) $$
(8)

assuming that source points are not contained in the same plane. RBF Morph operates the smoothing of mesh nodes with the formulation of the interpolant:

$$ \left\{ \begin{gathered} s_{x} \left( x \right) = \sum\limits_{i = 1}^{N} {\gamma_{i}^{x} \varphi \left( {x - x_{si} } \right) + \beta_{0}^{x} + \beta_{1}^{x} x + \beta_{2}^{x} y + \beta_{3}^{x} z} \hfill \\ s_{y} \left( x \right) = \sum\limits_{i = 1}^{N} {\gamma_{i}^{y} \varphi \left( {x - x_{si} } \right) + \beta_{0}^{y} + \beta_{1}^{y} x + \beta_{2}^{y} y + \beta_{3}^{y} z} \hfill \\ s_{z} \left( x \right) = \sum\limits_{i = 1}^{N} {\gamma_{i}^{z} \varphi \left( {x - x_{si} } \right) + \beta_{0}^{z} + \beta_{1}^{z} x + \beta_{2}^{z} y + \beta_{3}^{z} z} \hfill \\ \end{gathered} \right. $$
(9)

Common radial functions are summarized in Table 1. The distance function (global supported and bi-harmonic in 3D), used by default, performs very well in volume morphing since reaching very good quality.

Table 1 RBF with global and compact support radial
Full size table

According to Eq. (9), every node of the volume mesh to be morphed has a new position computed in a meshless way using as input just its original position and the RBF expansion (Eq. 10):

$$ x_{{node_{new} }} = x_{node} + \left[ {\begin{array}{*{20}c} {s_{x} \left( {x_{node} } \right)} \\ {s_{y} \left( {x_{node} } \right)} \\ {s_{z} \left( {x_{node} } \right)} \\ \end{array} } \right] $$
(10)

2.3 Structural-CFD set-up analysis

Using the commercial tools ANSYS Mechanical® with the ACT RBF Morph™ plugin extension and ANSYS- CFD® (ANSYS Inc., Canonsburg, PA, USA) a fluid-dynamics analysis coupled with finite element structural analysis of the flexible components of assembled systems was carried out through a 2-way Structural-CFD simulation, synthesized in Fig. 3.

Fig. 3
figure 3

Workflow of 2-way structural-CFD analysis

Full size image

The process start with the CFD analysis of the baseline of flexible components at the design conditions. A mapping procedure was then applied to transfer the fluid-dynamic loads to FE model of flexible components. The structural analysis solution, in terms of flexible components deformations, was used in order to update the fluid dynamic domain according to the estimated deformed shape. The CFD computation was restarted on the new configuration and the cycle continued until the flexible components deformed shape (for a steady condition) was reached.

In this loop in which CFD and Structural analyses exchanged geometrical data a proper Mesh updating with RBF allowed to edit shape and size of flexible components in order to maximize the system's ability to absorb or store energy.

In the FE model frictional contact formulation using CONTA175 and TARGE169 elements was adopted. Static and dynamic frictional coefficients were set as 0.2. Thus, contact pair component (also flexible) could slide and separate.

2.4 RBF parameters

Taking into account the results obtained from the Structural-CFD analysis for the baseline geometrical configuration of flexible components, the changes in shape and size were applied to the geometry of the flexible components according to the geometrical specifications and tolerances. The RBF solutions related to these changes were generated using the 'Surfs' and 'Encap' features of RBF Morph ™ [30]. In particular, for each shape modification a set of surfaces “Surfs” was used to fix the nodes that are required not to change their position, a cylindrical “Encap” to deform the surfaces inside a proper domain, limiting the morphing action while respecting the tolerances.

2.5 Specific energy

2.5.1 Y absorption

The evaluation of the ratio of the energy absorbed by the system to the mass of the flexible components measured the specific energy absorption (SEA) during the crushing process. SEA can be expressed as Eq. (11) and evaluated during the structural-CFD analysis. A higher SEA indicates higher exploitation of material usage for energy-absorption and efficiency of the AS-FC design.

$$ SEA = \frac{{\mathop \smallint \nolimits_{0}^{d} F\left( x \right)dx}}{m} $$
(11)

The above-mentioned method was used to maximize the SEA of an automotive crash shock absorber. In the next section the values of the main parameters were evaluated and the potential of the proposed method was discussed.

3 CASE STUDY: the crash shock absorber

The crash shock absorber (Fig. 4) is a mechanical energy storage device in which a piston (or a leaf spring) moves (and/or deforms) within charged viscoelastic polymer blend to develop a damper force over an axial displacement.

Fig. 4
figure 4

Car rear bumper crash shock absorber

Full size image

The geometric shape of its three assembled components (sheath, stem and leaf spring) determines this axial displacement between the point “A” of the stem and the point “B” of the sheath (Fig. 5a) and the maximum energy the crash absorber can dissipate (green area in Fig. 5b). The leaf spring sliding and deforming within charged viscoelastic polymer blends inside the sheath produces the parabolic force response dissipating energy.

Fig. 5
figure 5

a Crash shock absorber FE model; b Dissipated energy

Full size image

A functional dimensioning of the components was carried out according to the standards ASME 14.5 [1] in order to provide, through geometric dimensioning and tolerancing (GD&T), those variations allowed for manufacturing in relation with the assembling conditions.

Setting a maximum stroke of 100 mm, a maximum crushing speed of 600 mm/s and a maximum acceptable value for the internal material stress of 300 MPa, a fluid–structure interaction analysis of the device was performed by using the commercial tools ANSYS Mechanical® with RBF Morph™ plugin extension and ANSYS-CFD®. Assuming the material properties as linearly elastic and transversely isotropic, a “morphing” study was performed by varying the transversal dimensions (width “l” and height “h”) of the leaf spring (Table 2). The MM formulation, applied at the same time to the constrained parts, allowed them to be modified while maintaining the coupling tolerance values shown in Fig. 6.

Table 2 Geometric variations of leaf spring transversal dimensions
Full size table
Fig. 6
figure 6

Functional dimensioning: a leaf spring; b stem; c sheath

Full size image

The discretized model is made of 256116 s order tetrahedrons (TET 10) elements SOLID 187 with 584359 nodes. In the leaf spring-sheath-stem contact zone a denser mesh with patch conformity was employed using element “CONTA 174” and “TARGA 170” (Fig. 7). These elements allowed to simulate the friction forces in the contacts. Using Remote Point formulation axial F external loads were applied on the device ends. Geometric parameterization based on RBF-MM implemented shape modifiers directly on the computational domain. The new geometric configurations resulted from the displacement of a mesh region, through the use of algorithms, based on RBFs, which smoothly propagated the imposed displacement to the surrounding volume.

Fig. 7
figure 7

Modified shape with morphing action

Full size image

The RBF interpolation functions drove the MM of the discretized domain of the computational models by applying predefined displacements in the set of 160 nodes (source points) near the contact zones between leaf spring and stem. During the MM the nodes on the external profile moved according to the defined constrain varying l and h dimension (Fig. 6). Then, the RBF action was extended in the entire volume, smoothing the grid up to the prescribed surrounding limits. The obtained RBF solution was sent to the ANSYS Mechanical solver and a relation force–displacement was consequently obtained.

4 Results

After validating the FE structural-fluidynamics model with an experimental quasi-static crushing test, the study contributed to enhance the understanding of the influence of geometry changes on dissipated energy.

The optimum values of leaf spring transversal dimensions reported in Table 2 allowed to increase of almost 1 kJ (by over 40%) the device capability of storing energy (light blue area in Fig. 5b).

Thanks to the described computational methodology, the performance of assembled system composed of flexible components was improved. The method, based on RBF-MM formulation, allowed to find the optimal geometry of the deformable components with respect to the original constraints and geometry of the assembly.

A proper tolerance specification made possible to manage the linear and volume variations of the components of the assembly, ensuring the desired functionality of the device.

5 Conclusions

In this paper, a radial basis functions (RBF) mesh morphing (MM) formulation in non-linear numerical finite element computational analysis (FEA), including contact problems and flow interaction, was reported. This research provides, directly in the FEA environment, a design method to optimize shape and size design parameters of flexible components used in AS-FC. The potentiality of the method and its forecasting capability were demonstrated for the case study of an automotive crash shock.

In the proposed method these important features were combined: the definition of the FEA mesh portions to be updated, and the interactive definition of the required movements (design parameters) of the points driving the shape deformation (source points); the propagation of the displacement prescribed on source points to the volume mesh target with smoothing effect.

Additionally, the paper focused on the specific energy absorption (SEA) maximization. In the system studied, an increase in SEA of over 40% was obtained. Two different geometrical modifications (Surfs and Encap) were simulated and the achieved results allowed for an optimal dimensioning.

The results obtained invite to extend the use of the proposed method also to further developments, e.g. for the optimization of mechanical components that dampen or absorb vibrations such as gears, supports, transmissions, chain drives, linkages, bearings, brakes, fasteners, sensors, cables, etc. in different mechanical systems (actuators, engines, transmission and transport systems, manufacturing systems, etc.).