Development of an image-based measurement instrument for gloss characterization

Abstract

Gloss is one of the main attributes to describe the appearance of surfaces and objects, as it contributes to the general quality perception. Gloss is a multidimensional quantity of which ‘specular gloss’ is the most commonly applied attribute. Specular gloss meters are standardized and widely used in industry. However, their readings correlate only partially to the general visual gloss impression, which also comprises distinctness-of-the-reflected-image (DOI), haze, contrast and surface-uniformity attributes. This study presents a more profound image-based gloss meter (iGM) which incorporates a CMOS camera detector. This concept is not new, but limited research has been conducted on the inclusion of various image processing evaluations for gloss attributes. The designed iGM is compatible to 60° specular gloss meter standards. The CMOS detector captures the reflected source image, which is processed to measure four perceptual attributes of surface gloss. The obtained results validate the 60° specular gloss evaluation and indicate a promising capability in characterizing DOI, haze, and contrast. Contrast is an important attribute that is not available yet in industrial gloss meters. It is measured using a diffuse aspecular light source. Generally, this iGM maintains the hardware principles of specular gloss meters, while evolving toward a representative gloss perception meter.

Introduction

In many applications, such as automotive and retail, customers assess the quality of a product mainly on its visual appearance. For the characterization of visual appearance, four basic attributes were put forward by the CIE, namely color, gloss, texture, and translucency.¹ This paper focuses on the measurement of gloss.

According to Hunter (1937), at least six perceptual attributes exist and can be applied for the total evaluation of gloss: ‘specular gloss’ (brilliance of the specular reflected light), ‘contrast gloss’ (contrast between specular reflecting areas and other areas), ‘Distinctness-Of-Image (DOI) gloss’ (distinctness and sharpness of the reflected image), ‘haze’ (semi-specular reflection adjacent to reflected images), ‘sheen’ (shininess at grazing angles), and ‘surface-texture-gloss’ (surface evenness, texture and recognizability of the presence of the surface).² Since Hunter, additional research revealed that these attributes were generally not independent: two to four attributes are typically sufficient to describe the perceived gloss in controlled circumstances.^3,4 On the other hand, additional attributes and instrumental features were also introduced, although some of them are highly related to Hunter’s perceptual classes. Orange peel, a typical effect that deteriorates the perception of spray painted surfaces, can for example be classified under Hunter’s surface-texture-gloss. Marlow et al. introduced the attributes ‘sharpness’ (related to Hunter’s DOI) and ‘contrast’ (related to Hunter’s contrast gloss), but also added ‘coverage’ (proportion of a surface that appears to be covered by specular reflection) and ‘depth’ (stereoscopic depth information due to binocular disparity) as new descriptors of the general gloss appraisal.⁵ A linear combination of these attributes explained 94% of the variance in perceived glossiness. ‘Specular edge’ (the structure around edges of specular reflecting areas),^6,7 ‘recognizability of the reflected image’ (related to DOI),⁸ ‘highlight strength’ (related to specular gloss),⁹ ‘dark gloss’ (visibility of dark structures from the environment in the surface reflection)⁷ and ‘gloss unevenness’ (related to surface-texture-gloss)¹⁰ are other examples of perceptual and/or instrumental attributes found in literature. The contribution of each of these attributes to the gloss impression also appears to be strongly case-specific and dependent on the experiment sample set.¹¹ In addition, the terminology for perceptual attributes is sometimes overlapping with the corresponding physical and instrumental metric.

In absence of a consensus, the authors selected five attributes which are considered to be vital for the instrumental characterization of gloss. They are largely related to Hunter’s categories: specular gloss, DOI, haze, contrast, and surface-uniformity gloss (consisting of gloss unevenness, surface texture, and orange peel).

Several metrics and instruments have been proposed for the physical measurement of these five perceptual attributes. A summary of some available metrics is listed in Table 1, including the metrics investigated in this study. Specular gloss meters measure the amount of the specular reflected light of a test sample in comparison to the specular reflected light from a reference sample. They are widely used in industry for quality control purposes and comply to dedicated metrological standards, which define the measurement of the ‘gloss value’ expressed in Gloss Units (GU).^12,13 For nonmetallic materials, three measurement geometries (60°, 20° and 85° angle of incidence) are defined. The specified angles describe the illumination and viewing angle to the surface normal. The 20° and 85° geometries are necessary to increase the distinguishing power of the gloss meter for high-gloss (above 70 GU at 60°) and matte samples (below 10 GU at 60°), respectively.¹³ In principle, it thus requires multiple specular gloss meter geometries to accurately distinguish samples across the entire gloss range. A measurement with a reference sample is assigned a value of 100 GU in each geometry, despite the high difference in specular reflection between each geometry. This leads to inconvenient differences in amount of gloss units between the geometries. However, many specular gloss meters are limited to the standard geometry of 60°. Next to the classical gloss value, specular gloss is also evaluated as the mean or peak luminance of regions with specular reflection within a scene or recorded image.9 This approach is mainly used in perceptual studies with complex objects, such as paintings, or studies with images displayed on computer screens.

Table 1 A summary of available measurement metrics is given for the selected perceptual attributes of surface gloss

Multiple standardized measurement methods are available for the measurement of DOI. These metrics are based on the signal value at specified off-specular angles close to the specular direction, or on the maximum and minimum light intensities that occur while sliding an optical mask with line patterns in front of the receptor.^14,15 Image-based metrics for DOI are often referred to as ‘sharpness’ or—its inverse—‘blurriness’ and are calculated as the steepness or width of the highlight edges from a recorded image.^5,16,17 Furthermore, DOI can also be determined from the Modulation Transfer Function (MTF), constructed as the Fourier transform of the Line Spread Function [derivative of the Edge Spread Function (ESF)].¹⁸ The ESF is obtained from the reflected image of an illumination mask with a sharp edge. Sharpness is then for example calculated as the bandwidth at a certain level of attenuation of the MTF. Finally, Hassen et al. developed a general image sharpness metric based on the local phase coherence of sharp image features.¹⁹ It has been used in multiple gloss studies for the calculation of the DOI attribute.^4,20

To determine haze, standardized methods use the luminous flux at approximately 2° off-specular angle from the specular direction in a 20° or 30° measurement geometry.^15,21 Haze is then calculated as the ratio of this luminous flux and the flux reflected by a gloss reference sample inside a particular region centered around the specular direction. Vangorp et al. introduced ‘Halo energy’ as an improved metric for perceptual haze. It is calculated as the energy surrounding a BRDF model function, which is fitted to the central reflection peak of the BRDF.²²

Contrast metrics are available for global (between two regions) and local (pixel-by-pixel) contrast. The global contrast definition by the CIE,²³ denoted as ‘psychometric contrast’ or ‘Weber contrast’, focuses on the ratio of the luminance levels of a target region compared to its background. Leloup et al. validated a contrast gloss formula for samples with a high DOI, based on a luminance contrast formula by Bodmann,²⁴ comprising the difference between the highlight and the surround compressed luminance values.²⁵ Tadmor et al. created a local contrast measure by combining a neurophysiological inspired Difference of Gaussian (DoG) kernel with global contrast definitions.²⁶ Marlow et al.⁵ found a good correlation between perceived contrast and the local contrast calculation method from Peli, which is based on the ratio between band-pass and low-pass filtered versions of an image.²⁷ The gloss studies by Storrs et al. and Schmid et al. used the sum of root-mean-squared (RMS) contrast of multiple band-passes of an image as a measure of the contrast.^4,20 However, there is no consensus yet on a single method for the evaluation of contrast of an arbitrary image.^23,28

Surface-uniformity gloss is divided into three sub-categories. Gloss unevenness is caused by variations in the glossy appearance of surfaces. This can be due to material damage, scratches and dirt inclusions. It is typically measured as the luminance variation in the highlight regions on a surface.¹⁰ Secondly, texture can be caused by physical structures on surfaces (physical texture) or structures beneath the transparent coating of surfaces (optical texture). Depending on the structure size, they are categorized as mesoscale (larger) and microscale (smaller) texture. Physical texture metrics are typically extracted from the 3D topology of surfaces. Optical texture is caused by mirror flakes added to the coating of surfaces. They cause spots with bright reflection at surface positions varying with the angle of viewing. This effect is also called sparkle and is for example quantized based on the contrast between the bright spots and their surround.^29,30,31 Finally, orange peel is caused by spatial profiles on the surface, giving it the appearance of the peel of an orange. It is typically extracted by capturing the reflection of a laser beam while moving over the surface. Orange peel metrics are calculated as the spatial Fourier transformation of this reflection profile within specific wavelength ranges.³²

In the past, each aspect of gloss required a separate evaluation instrument. However, using the advancing technological development in image sensors and image processing hardware and software, portable instruments have recently been designed that capture and evaluate multiple attributes of surface gloss in a single measurement geometry. Some instruments maintain compliance to specular gloss, DOI and haze standards, and others include new processing methods. However, most methods applied by instrument manufacturers are still closely correlated to the international standards. The ‘Surface reflectance analyzer’ from Canon is capable of measuring specular gloss, DOI, haze, and estimations of physical reflection characteristics of surfaces using CMOS sensors.³³ Besides specular gloss, the ‘IQ’ from Rhopoint Instruments includes a 1D photodiode array to capture the peak luminance of the reflected image and to evaluate DOI and haze.³⁴ The ‘Wave-Scan’ from BYK Gardner combines the measurement of DOI with surface-uniformity (orange peel) for high gloss surfaces.³⁵ The CCD sensor in the ‘BYK-mac i’ captures information on physical and optical texture with diffuse and directional illumination.³⁶ Their ‘spectro2profiler’ measures, apart from specular gloss, surface-uniformity metrics of matte surfaces with both the illumination and the CMOS camera at the normal direction to the surface.³⁷ Inoue et al. proposed a gloss evaluation instrument with a linear light source and a CCD camera for the measurement of surface-uniformity (gloss unevenness and scratches) of surfaces.^10,38 Leloup et al. presented and validated the concept of measuring specular gloss with a CMOS sensor capturing images of the surface of samples.³⁹ Contrast gloss was measured by adding a diffuse aspecular light source for background illumination. Orange peel could be visualized from sample surface pictures.

This paper describes an image-based gloss meter (iGM) that is capable of evaluating metrics for at least four (specular gloss, DOI, haze, and contrast) of the five attributes presented above. Compliance to international ASTM and ISO standards for specular gloss at 60° is considered as essential for acceptance by the industrial market, as this provides backward compatibility with traditional specular gloss meters. The design is based on a 60° parallel-beam gloss meter and uses a CMOS imaging sensor that is focused on the rectangular source aperture of the gloss meter. The availability of source-focused information makes the instrument well suited for the evaluation of DOI and haze. Similar to previous work, an additional aspecular light source is added perpendicular to the sample surface to include the measurement of a contrast metric.³⁹ Such a contrast measurement is, to the best of our knowledge, not available in any industrial specular gloss meter yet. Furthermore, the presented instrument incorporates gloss attribute metrics requiring more advanced image processing methods into an industrial gloss meter, which opens opportunities for a more profound characterization of gloss. The results for specular gloss, DOI, haze, and contrast are compared to readings obtained with existing instrumentation (if available) on appropriate sample sets to illustrate the added value of the iGM and the appropriateness of the metrics.

Design of the iGM

The next two sections describe the design, build (current section) and optical characterization (next section) of the iGM meter. The optical design and the iGM prototype are presented in Figs. 1 and 3, respectively. The section on results then introduces and exemplifies the capabilities of the iGM in evaluating gloss metrics.

Fig. 1

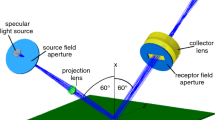
Source aperture/3&4: Source and receptor lens/5: Test surface/6: CMOS sensor/7: Receptor field stop region/8: Image of source aperture/9&10: Optical axis of incident and receptor beam/11: Aspecular light source/12: Direction of measurement/θ_s: Source image aperture angle/θ_r: Receptor field stop angle)

The gloss instrument geometry, based on ISO 2813 (2014)¹³ (1: Specular light source/2:

Optical design

International standards for specular gloss, DOI, and haze meters describe dedicated measurement geometries, including illumination and measurement angles and aperture sizes. The basic optical design of the new instrument is largely relying on the 60° geometry encountered in commercial specular gloss meters. It is known from literature that measurements obtained in the 60° geometry have a good correlation with the perception of gloss.^3,40,41 This choice removes the inconvenience of the uncorrelated measurement scales corresponding with each angle of incidence (60°, but also 20° and 85°). A single geometry also promotes the use of more advanced optical components, which boosts the precision and imaging quality of instruments. The parallel-beam geometry for specular gloss meters, standardized in ISO 2813 and ASTM D523, was selected. In spite of the converging-beam variant, only this geometry is complying to both standards.^12,13

The optical design of the instrument is shown in Fig. 1. One of the main components of the setup is the camera sensor. As classical specular gloss meters use cheap silicon photodiodes, it is desirable to limit the cost of the camera sensor while maintaining high precision. A camera board was selected taking cost, optical dimensions, resolution, signal-to-noise ratio (SNR), pixel dynamic range, and quantum efficiency into consideration. It comprises a 5MP (1/2.5”) color CMOS sensor with 2.2 µm pixel pitch.¹ The camera is connected to MATLAB via the GenIcam interface and a MATLAB app provides flexible functions to capture and process the pictures. The sensor read-out consists of the raw 8 bit data and its gain and digital gain are both set to unity. The exposure time of the rolling electronic shutter remains the only adjustable parameter. The image demosaicing is performed on the sensor board before read-out.

In a specular gloss meter, the light emerging from a physical and standardized receptor field stop is captured by a photodiode for the measurement of specular gloss. In this setup, the physical receptor field stop is omitted and a rectangular region of pixels (item 7 in Fig. 1) on the sensor surface is attributed to it. The region fits within the sensor dimensions with some margin to account for sample mispositioning and slightly curved samples.

The instrument dimensions should be similar to existing portable gloss meters. A suitable focal length² for the receptor lens can be calculated from the standardized receptor field stop angles^12,13 (θ_r in Fig. 1), because the receptor field stop must be positioned in the focal plane of the receptor lens. The size of the receptor field stop thus increases with the focal length of the receptor lens, and it must fit within the sensor dimensions. The same focal length is used for the source lens so that the total magnification of the system equals unity. The two achromatic lenses were purchased off the shelf. Spherical aberrations are minimized by limiting their free optical diameter. An equal optical path length—between the source and sample, and between the sample and sensor—ensures the device symmetry.

The rectangular source aperture (item 2 in Fig. 1), defined by the standards, is imaged in the middle of the receptor field stop sensor area. This component is manufactured with metal deposition on a glass substrate. As the source aperture is not a point source, the collimated beam between the source and receptor lenses is slightly diverging. To avoid vignetting effects in the source aperture image, the free optical diameter of the receptor lens must therefore be larger than that of the source lens.

The light beam emerging from the source aperture is collimated by the source lens, creating an oval-shaped illumination spot on the surface of approximately 8 mm × 17 mm in the out-of-plane and in-plane reflection direction, respectively.

A 5 mm white LED and a Xicato XSM LED source act as the specular and aspecular light source (item 1 and 11 in Fig. 1), respectively. They are powered with constant current power sources. The aspecular light source is positioned at the normal of the sample surface (0°) and several volumetric diffusers allow for a uniform surface illumination within the region of interest.

Spectral characteristics

Spectral filtering is essential for gloss measurement when evaluating matte, highly chromatic samples, as the reflection of these surfaces is spectrally selective. However, it is less relevant for nondielectric high gloss samples and for achromatic samples—whose reflection spectra are nonselective.¹²

According to the international standards, the light source of a specular gloss meter must have the spectrum of the CIE standard illuminant C and the detector’s spectral response should match the CIE luminous efficiency function V(λ).^12,13 The ISO 2813 standard describes a filter to correct for spectral mismatches of the source and the detector simultaneously, which makes the requirements less stringent, as the wide spectrum of illuminant C is being cut off by the V(λ)-detector. Gloss meters nowadays use LED light sources because of the increased lifetime and reduced power consumption. Typical LED spectra however majorly deviate from the illuminant C spectrum and there is no standardized LED spectrum for gloss meters yet. However, the CIE Technical Committee 2-90 selected the LED-B3 spectrum as the most suitable LED reference spectrum for general photometric measurements.⁴² In order to encourage standardization, an LED with a spectrum similar to LED-B3 was selected. The green channel of the RGB sensor is used as receptor, as the spectral quantum efficiency curves (available in the datasheet) indicate that this channel already approximates the CIE luminous efficiency. However, the quantum efficiency increases again at wavelengths above 700 nm, demanding a cut-off filter. Figure 2 indicates the target and actual combined source-detector spectral responsivity as calculated from the specifications. Two filters, one for the LED’s blue peak around 450 nm and an IR cut-off at 700 nm, were selected off the shelf. The resulting filtered spectral response is included in Fig. 2. Since there is no method specified to evaluate the spectral deviations of gloss meters, the weighted rms error metric proposed by Imai et al.⁴³ and the measure of goodness for spectral vector similarity proposed by Vora et al.⁴⁴ were calculated. The rms error metric decreases from 0.65 for the response without filters to 0.14 for the filtered response, while the measure of goodness for spectral vector similarity increases from 0.93 to 0.96. Although no absolute threshold values do exist, both metrics thus indicate an improvement due to filtering and the obtained spectral similarity seems to be acceptable. The filters are preferably placed in front of the receptor, where the IR filter avoids influences of the sample surface temperature.⁴⁵ The National Physical Laboratory indicates however that this preference is merely to avoid heating influences at the source location with prior light source technologies. For the ease of application, the filter for the blue peak and the IR filter are placed in front of the source LED and the CMOS detector, respectively.

Fig. 2

Spectral response of the iGM. The required spectral behavior, actual spectral behavior, and behavior after filtering are indicated with a thin dashed line, a thick dashed line, and a thick dotted line, respectively. All curves are scaled to a maximum value of 1

The aspecular source has a CCT of 3000K and a CRI of 80. No additional filtering is currently performed on this source. However, for commercialization purposes the use of an identical light source/filter combination for both the specular and aspecular source is preferential and envisaged.

Mechanical design

An optical test bench was designed (see Fig. 3), consisting of an optical base plate with rails and 3D printed component holders. Test samples are installed against a vertical support plate and tightened with flexible levers. Both the angle of incidence and reflection can be finetuned. The holders are adjustable in the plane perpendicular to the rail and can slide along the rail. Manual alignment is required to obtain a sharp image of the source aperture. All components are baffled with matte, black paper to avoid stray light. Figure 3 only shows the stray light baffle for the aspecular source, other baffles were removed when taking the picture.

Fig. 3

source with filter/2: Source aperture/3: Source lens/4: Sample holder/5: Test sample/6: Stray light baffle/7: Aspecular source with diffuser/8: Receptor lens/9: CMOS sensor board with IR filter

Test bench: 1: Specular LED

Characterization of the iGM

To evaluate the temporal stability of the system, 60 images of a high gloss standard sample (illuminated by the specular source) were captured every 30 s during a period of 30 min, after an initial 30 min warm-up. The standard deviation of the raw data integrated for all pixels for the 60 images is only 0.011 % for the green channel and similar for the other channels. Similar results are obtained for the aspecular source.

The relation between the sensor signal and the applied exposure time was also examined on the same high gloss standard sample in multiple exposure time intervals over the available range of 16 µs to 1048 ms. In each interval, the specular light source was powered with a suitable source current to avoid pixel saturation. An illustration of the linearity of the green channel recorded in the interval from 5 to 120 ms is shown in Fig. 4a. The mean pixel values have an excellent linear behavior with the exposure time for each interval and channel. The intercept value represents the read-out noise of the camera sensor and will be subtracted later with a dark signal correction. In addition, the presence of a nonlinear gamma correction in the sensor signal processing was tested by evaluating a white, light gray, dark gray, and black sample of the NCS gloss scale sample set⁴⁶ at a constant exposure time of 115 ms. The samples were installed on the test bench of Fig. 3 and illuminated with the diffuse aspecular light source. The receptor lens and CMOS sensor holders were repositioned along the rail to obtain a camera view focused on the sample surface. In Fig. 4b, the average pixel value (of the green channel) in a centered region of the measurement image is displayed against the average spectral reflectance of each sample, measured with a Hunterlab UltraScan Pro spectrophotometer in the d:8° geometry (Specular component excluded). The relationship is highly linear for each color channel with a similar intercept as observed in Fig. 4a. The sensor thus has a general linear behavior and the opto-electronic conversion function does not need to be determined.⁴⁷

Fig. 4

(a) The sensor average pixel value (of the green sensor channel) versus the exposure time, from 5 to 120 ms. The cross marks indicate the measurement points and are bolded when saturated pixels are available in the image. (b) The sensor average pixel value (green sensor channel) versus the average specular reflectance for samples with different lightness values. (c) The sensor dark signal of the green channel (average pixel value of a nonilluminated sensor) approximately has a linear relation to the exposure time at constant temperature. The dashed lines indicate the linear relationships (Color figure online)

The dark signal of the sensor channels after warm-up is also evaluated over the exposure time range as the mean pixel signal over all sensor pixels. It increases approximately linear with the exposure time with a slope (which is dependent on the sensor temperature) of 0.026 counts/s (Fig. 4c) for the green channel.⁴⁸ The intercept (typical 1 count) again reflects the read-out noise.

The full dynamic range of the sensor pixels and minimal signal-to-noise ratio is obtained at the maximum exposure time avoiding saturation. A selection algorithm for this optimum exposure time precedes each measurement. This algorithm first selects an exposure time for which there is no saturation and (at least) a region of pixels that has a signal considerably higher than the dark signal. Making use of the linearity between the pixel signal and the exposure time, the optimum exposure time is estimated. Each measurement is accompanied by a dark image (light sources switched off) to accurately determine the dark signal of every pixel.

Finally, the dark signal is subtracted from the pixel signal (pixel by pixel) and the result is divided by the exposure time of the capture. This ‘transformed’ pixel signal of the green channel is used for all further analysis in this work. It is proportional to the illuminance onto the pixel, and yet to the luminance of the corresponding position within the source aperture and will be denoted as ‘sensor signal’ or ‘pixel signal’.

Results

Test samples

For the specular gloss calibration of the test bench, a calibrated reference tile (black glass) of 103.2 GU in the 60° geometry is utilized. Three sample sets were used for investigating the measurement capabilities related to specular gloss, DOI, haze, and contrast. Set 1 consists of a custom-made specular gloss sample set with narrow tolerances (produced by NCS), and encompasses eleven black paint paper samples covering a specular gloss range between 2 and 93 GU. Set 2 comprises the commercial NCS gloss scale,⁴⁶ and is composed of 28 achromatic paper samples at seven gloss levels between 2 and 95 GU in combination with four lightness levels (white W, light gray LG, dark gray DG, black B). Set 3 contains six glass samples which were processed with a black (painted) back side, and etched and polished front side to obtain various levels of specular gloss within the range of 5 to 93 GU.

To avoid the influence of sample curvature, all paper samples were glued to a 4 mm thick PMMA plate with fast curing aerosol glue. Three fixed measurement positions were selected on each sample. All presented results consist of average values of measurements at these 3 positions.

Specular gloss

The standardized specular gloss metric is the ‘gloss value’ expressed in ‘gloss units’ (GU). As it is commonly used in classical gloss meters, its inclusion in the iGM is vital for a wide acceptance in the relevant user community.

To determine the gloss value, the image reflected by the sample is captured. As indicated in Fig. 1, the receptor field stop used for gloss evaluation consists of a particular region on the camera sensor. This region is centered around the position of the “center of mass” of the image, which is located nearby the center pixel in normal circumstances. The iGM displays a warning message in case of a high deviation, which might be an indication for instrument misalignments or deformed samples. The pixel signal of each pixel inside the receptor field stop is added and stored. In the same way, the reference sample (black glass) is measured. The ratio of both values is multiplied with the labeled gloss value of the reference sample.

Specular gloss values obtained with the iGM are validated by comparing them with the results obtained from equivalent measurements with two commercial gloss meters (IQ from Rhopoint Instruments and micro-TRI gloss from BYK-Gardner) for sample set 1 and 2. The results are gathered in Table 2. The mean specular gloss difference of the iGM with the IQ and micro-TRI gloss is 1.3 GU and 1.1 GU, with a maximum difference of 3.3 GU and 2.4 GU, respectively. The standard deviation over the three sample positions of each sample is similar for each instrument. The results also indicate a considerably higher nonuniformity for the second sample set. Overall, the mid-gloss region seems most prone to deviations between the instruments. An observation that was also reported in a study by Leloup et al.⁴⁹ Furthermore, they obtained repeatability and reproducibility data of gloss meters between different manufacturers by use of similar sample sets that reached up to 8.3 GU and 10 GU, respectively. Consequently, the performance of the iGM regarding specular gloss is very good and in line with the results obtained with classical and dedicated specular gloss meters.

Table 2 Comparison of the gloss values, for the first two samples sets, obtained with the iGM, the Rhopoint IQ (GM1) and the BYK-Gardner micro-TRI gloss meter (GM2)

Distinctness-of-image (DOI)

The samples of sample set 1 and sample set 3 are used for the investigation of DOI. By way of example, the source aperture images taken by the iGM are shown in Fig. 5 for a matte (approx. 10 GU), semi-high-gloss (approx. 70 GU), and high-gloss (approx. 95 GU) sample of set 1 (upper row: 1.1–1.3) and set 3 (lower row: 3.1–3.3). In addition, signal lines parallel and perpendicular to the incident plane are calculated as an average over the columns and rows containing the imaged source aperture, respectively, and presented in Fig. 5 against the relative off-specular angle. In both planes, this off-specular angle is the angle between the optical axis (see item 10 on Fig. 1) and a connection line from the intercept of items 9 and 10 to the pixel position on the sensor. Measurement noise is reduced by applying a Gaussian filter (σ = 10 pixels).

Fig. 5

The measurement images captured with the iGM and corresponding (absolute) parallel and perpendicular signal lines are given for three examples of sample set 1 (1.1–1.3) and 3 (3.1–3.3), with a specular gloss of approx. 10 GU (X.1), 70 GU (X.2), and 95 GU (X.3). The vertical and horizontal direction in the images represents the direction parallel and perpendicular to the incidence plane, respectively. The signal lines are plotted against the relative off-specular angle in the corresponding plane (relative to 60° in the parallel plane; relative to 0° in the perpendicular plane)

The image sharpness can be considered as an image-based metric for DOI and is calculated from the three-point-derivative (the slope) of the horizontal or vertical signal line, normalized to a maximum value of one. The mean of the maximum upward and downward slope value (absolute values) is taken. Similar to the specular gloss value, this mean value is rescaled to obtain an iGM ‘slope sharpness’ of 100 SU (Sharpness Units) in the parallel and perpendicular directions for the reference tile for specular gloss. This results in a parallel and perpendicular slope sharpness, S_parallel and S_{perpendicular}, respectively.

The slope sharpness values from the iGM (60° geometry) are compared to DOI evaluations with a commercial gloss meter (IQ from Rhopoint Instruments), which applies a measurement principle similar to the ASTM (E430 & D5767) standards for DOI at a 20° geometry, further denoted as ‘IQ-DOI’:^14,15

$${\it\text{IQ-DOI }} = \left( {1 - \frac{{F_{os,0.3^\circ } }}{{F_{s,20^\circ } }}} \right)*100\%$$

(1)

F_os,0.3° is the average luminous flux in a region centered around 0.3° off-specular interval at both side of the 20° specular peak and F_s,20° is the average flux in an interval centered around the peak.

As the standards consider DOI only in the plane of incidence, the values of S_parallel and IQ-DOI for all samples of set 1 and set 3 are compared in Fig. 6. The values show a large overlap in IQ-DOI between both sample sets, while S_parallel is much higher for almost every sample of set 3 compared to set 1. This finding is confirmed and demonstrated in Fig. 5: the distinctness of the reflected image is higher for each displayed sample of sample set 3 compared to any sample of sample set 1. In addition, a monotonic relationship is noticed in Fig. 6 for both sample sets, despite the high discrepancy between the two methods: the IQ-DOI of equation (1) is calculated independent of the observed edge sharpness in between the regions for F_os and F_s. This for example explains the steep increase in IQ-DOI, opposed to a slight increase in S_parallel, between sample (3.2) and its adjacent sample (with an IQ-DOI value of approx. 70 %). The error bars in Fig. 6 indicate the standard deviation over the measured positions of the samples. The maximum standard deviation is 2.6 % and 1.5 SU for IQ-DOI and S_parallel, resp. These findings suggest that an imaged-based sharpness metric might lead to a more appropriate representation of “distinctness of image” than the standardized conventional DOI metric. This however needs further investigation through psychophysical scaling with visual ratings from observers. From Fig. 5, it is also clear that samples with identical specular gloss can have a highly different DOI. This result is not surprising, as the specular gloss is based on the amount of reflected light within a large window while the DOI is depending on its local spatial variations.

Fig. 6

The results of the iGM parallel slope sharpness against the IQ-DOI are plotted for all samples of set 1 and 3, with white and black circles, respectively. The markers are connected with lines according to increasing IQ-DOI. The horizontal and vertical error bars indicate the standard deviation (−σ to +σ) over the measurement positions of each sample. The labels 1.1–1.3 and 3.1–3.3 represent the samples of sample set 1 and 3 that are discussed in Fig. 5

The availability of 2D images offers additional information compared to classical instruments. From Fig. 5, it becomes clear that the reflection characteristics and the corresponding S_parallel and S_{perpendicular} values of paper (sample set 1) can be quite different in both measurement directions, while the values of glass (sample set 3) are approximately equal. For further illustration of this effect, measurements were performed on a rolled aluminum reflector (1100G from Alanod GmbH) exhibiting strong anisotropy. In Fig. 7, the image of the source aperture after reflection on the aluminum surface is presented, when the incident plane is parallel to (Fig. 7a) and perpendicular to (Fig. 7b) the rolling direction. The DOI measurement results are summarized in Table 3. Clearly, both pictures and the resulting measurements show important differences. When the plane of incidence of the iGM is oriented parallel to the rolling direction, the specular peak is much more pronounced and centralized around the 60° reflection angle. In contrast, when the plane of incidence is perpendicular to the rolling direction, a huge difference in scattering and steepness occurs. This difference in the 2D behavior cannot be retrieved from a conventional instrument, since a rotation of the sample or instrument over 90° does not yield the out-of-plane scattering characteristics.

Fig. 7

The captured images and (absolute) parallel and perpendicular signal lines are given when orienting the plane of incidence of the iGM (a) parallel to and (b) perpendicular to the rolling direction of an Alanod Aluminum sample. The vertical and horizontal direction in the images represents the direction parallel and perpendicular to the incidence plane of the iGM, respectively. The signal lines are plotted against the relative off-specular angle in the corresponding plane (relative to 60° in the parallel plane; relative to 0° in the perpendicular plane)

Table 3 Measurements results for DOI and haze (see below section) metrics on the Alanod 1100G sample are presented for the IQ and the iGM.

Haze

The ASTM E430 and ISO 13803 standards describe haze evaluation methods in the plane of incidence at 20° [see equation (2)] as the ratio of the luminous flux in off-specular regions centered at 2° angle at both sides from the specular peak (F_{os,2°,sample}), to the flux reflected by the specular gloss reference sample inside the specular gloss receptor field stop (F_s,20°,ref).^15,21 Haze is then converted to logHaze in a logarithmic scale:

$${Haze} = \left( {\frac{{F_{{os,{2^\circ} ,{\text{sample}}}} }}{{F_{{s,{20^\circ} ,{\text{ref}}}} }}} \right)*100\% \quad \quad {logHaze } = 1285*\log \left( {\frac{{{Haze}}}{20} + 1} \right)$$

(2)

These off-specular haze regions however majorly differ between the standards, as ASTM defines the 2° off-specular angle from the sample surface and ISO from the receptor lens. This suggests that the exact position and size of the haze regions might not be crucial for a representative haze evaluation. The authors of this work attempted to measure haze in a similar way on the iGM (iGM-Haze) in the incident plane at 60° with arbitrarily selected haze regions from 2° to 4° off-specular angle (from the receptor lens). The ‘iGM-logHaze’ was expressed in a logarithmic scale using a similar principle as equation (2):

$${\it{iGM{\text{-}}logHaze}} = k*{\text{log}}\left( {\frac{{iGM{\text{-}}Haze}}{60} + 1} \right)$$

(3)

k = 2348 to obtain an iGM-logHaze value of 1000 when iGM-Haze equals 100. A HDR capture mode was introduced in the iGM in order to measure the small off-specular signal for high-gloss samples accurately. For all samples of set 1 and set 3, the iGM-logHaze was compared to haze values obtained with the IQ, denoted as ‘IQ-logHaze’, which applies the measurement principle of equation (2). Both the IQ-logHaze and the iGM-logHaze show a similar trend in the haze evaluation (displayed in Fig. 8a, b for sample set 1 and 3), with a low haziness for matte and high-gloss samples and a maximum haziness for mid-gloss samples. This result could be explained from equation (2): Haze follows the same trend as the side signal F_{os,2°,sample}, because F_s,20°,ref is a constant value. It is however clearly different from visual observations of the samples indicated in Fig. 5, where the perceptual haziness is increasing from high-gloss up to matte samples. In addition, the more steeply decreasing off-specular signal of sample (1.2) results in an almost three times lower IQ-logHaze compared to sample (3.2), while Fig. 5 suggests that the large haze signal close to the edge of the source aperture of sample (1.2) also influences the perceived haziness.

Fig. 8

The IQ-logHaze (left ordinate) and iGM-logHaze (right ordinate) are displayed against the sample number for sample set 1 (a) and sample set 3 (b). Graphs (c) and (d) contain the parallel Michelson contrast haze. The samples are ranked according to increasing specular gloss value. The vertical error bars indicate the standard deviation (−σ to +σ) over the measurement positions of each sample (σ is mostly too small to be visible). The sample numbers labeled with 1.1–1.3 and 3.1–3.3 describe the samples of set 1 and set 3 displayed in Fig. 5

Therefore, ‘Michelson contrast haze’ (H_MC) is proposed as an alternative metric for haze, inspired by the transparency haze metric of Busato et al. They calculate transparency haze as the Michelson contrast between two specified regions at each side of the edge in the ESF.^50,51 Accordingly, H_MC is determined from the signal lines as the Michelson contrast (MC) between both sides of the edges of the source aperture image. The metric is expressed in Haze Units (HU):

$${{H}_{\text{MC}}} = \left( {1 - \frac{{MC}_{\text{sample}}}{{MC}_{\text{ref}}}} \right)*100{\text{ HU}}\quad {MC} = \frac{{N_{{{\text{in}}}} - N_{{{\text{out}}}} }}{{N_{{{\text{in}}}} + N_{{{\text{out}}}} }}$$

(4)

$N_{{{\text{in}}}}$ and $N_{{{\text{out}}}}$ are the mean pixel signal over 100 pixels inside and outside the source aperture image. A margin of 40 pixels is ignored at each side of the imaged edge to decouple the data used for the haze calculation to that of the slope sharpness calculation. The Michelson contrast of the specular gloss reference sample equals unity in both planes, and is selected as the reference MC_ref. The iGM evaluates this metric in the parallel and perpendicular instrument plane, denoted as H_{MC_parallel} and H_{MC_perpendicular}, respectively.

The H_{MC_parallel} metric, measured on all samples of sample set 1 and 3, is displayed in Fig. 8c, d. For each sample set a clear correlation is observed between IQ-logHaze and H_{MC_parallel} from the mid to high gloss region. However, opposed to the IQ-logHaze, the Michelson contrast haze decreases monotonically for both sample sets from 100% for matte samples to a low value for the high-gloss samples. Furthermore, the difference in H_{MC_parallel} for the samples (1.2) and (3.2) is much lower (approx. 10 HU) compared to the earlier observed difference in IQ-logHaze. The error bars in Fig. 8 indicate the standard deviation over the measured positions of the samples. The standard deviation is generally small with maximum values for the tested samples sets of 14 and 12 for IQ-logHaze and iGM-logHaze and 2.2 HU for H_{MC_parallel}, respectively.

These observations illustrate the opportunity of an image-based haze metric for a better representation of the sample haziness compared to the standardized methods.

Michelson contrast haze is also evaluated in the perpendicular direction (H_{MC_perpendicular}). The H_MC values of both sample sets (set 1 and set 3) are generally smaller in the perpendicular plane compared to the parallel plane, which can already be expected from the visual observations in Fig. 5. Furthermore, the observed visual differences between the parallel and perpendicular directions for the samples of set 3, which did not imply differences in the measured parallel versus perpendicular slope sharpness, are clearly measured as differences in Michelson contrast haze. An anisotropy in haze can be evaluated in a similar way to the slope sharpness. The measurement results for the Aluminum Alanod sample in Fig. 7 are included in Table 3. The iGM can determine a visual directionality for haze in both the viewing directions parallel and perpendicular to the rolling direction, which cannot be determined with the evaluations of a conventional instrument.

Contrast

There is no commercial instrument with contrast evaluation available yet. In this work, we introduce the psychometric contrast into the iGM, which describes the contrast between a centered highlight (with luminance L_hl) and its background (with luminance L_b):^23,26

$$C_{psy} = \frac{{L_{hl} - L_{b} }}{{L_{b} }}$$

(5)

In the particular case of the iGM, it represents the contrast of the imaged source aperture against the background luminance Y (part of the XYZ color space) of a sample. In order to measure information on Y, the sample surface is illuminated with the diffuse aspecular source (item 11 in Fig. 1). Inspired by the contrast formula in equation (5), the iGM measures the contrast as iGM-C:

$${\it\text{iGM-C}} = \frac{{N_{hl} - N_{b} }}{{N_{b} }} = \frac{{N_{s,hl} }}{{N_{a} }} .$$

(6)

N_hl is the mean signal over a number of highlight pixels within a highlight mask covering the source aperture (see Fig. 9a). N_b is the mean signal outside the specular region on the sensor. For samples with lower gloss however, such as sample (1.1) in Fig. 5, N_b is influenced by the large scattering of the specular light source. A more accurate evaluation is preferred where the numerator and denominator of equation (6) are captured independently with specular (N_s,hl) and aspecular (N_a) source illumination, respectively, where N_a is the mean signal in a center region of the picture with aspecular source illumination. The iGM-C is referenced to a value of 100 CU (Contrast Units) for the reference tile for specular gloss, which makes the metric independent of the light level settings of both sources. To minimize the power consumption, the aspecular source is powered with the minimum current where the N_a signal of a high gloss black sample can still be detected.

Fig. 9

source is not visible compared to the bright specular highlight). The sensor signal is shown in gray values, the selected highlight pixels for N_hl (or N_s,hl) are colored in blue. (b) The iGM contrast (log scale) is displayed for each achromatic color against the GU label of the samples of set 2. Black (B), dark gray (DG), light gray (LG), and white (W) samples are indicated with circles in a matching color. Samples with equal color are connected with lines. The vertical error bars indicate the standard deviation (− σ to +σ) over the measurement positions of each sample (σ is mostly too small to be visible) (Color figure online)

(a) Measurement image of the W 75 GU sample illuminated by both sources (influence of the aspecular

The performance of the iGM contrast was investigated with the samples of set 2, which consists of achromatic samples with different gloss level at 4 distinct lightness levels, as discussed earlier. In Fig. 9b, the iGM-C values of the samples with the different lightness are plotted against their GU label. The sample with the same lightness are connected with lines. The iGM-C monotonically increases from light to dark backgrounds and from low to high specular gloss, with the lowest and highest value for the W 2 GU and B 95 GU samples, respectively. This is in line with expectations for the contrast between the highlight and the diffusely illuminated sample region. The similar contrast value of the LG and DG 30 GU samples is caused by the much higher specular gloss of the LG sample compared to the remaining samples with the 30 GU label (see Table 2). The standard deviation over the measurement positions of the iGM contrast (see error bars in Fig. 9b) is generally very small with a maximum value of 4.5 CU.

The obtained results illustrate the feasibility of contrast evaluation with an image-based gloss meter and the appropriateness of the proposed iGM-C contrast metric.

Conclusions

An image-based gloss meter (iGM) was developed using a CMOS detector and adopting a 60°:60° and 0°:60° measurement geometry. The iGM complies to the ASTM and ISO standards for 60° specular gloss to guarantee backward compatibility with industrial instruments. This was validated in comparison to multiple commercial specular gloss meters. In addition, the instrument processes the measurement images to evaluate the perceptual gloss attributes DOI, haze and contrast. The DOI was measured as the steepness of the slope at the edges of the imaged source aperture and correlated well with the standardized method for DOI. Furthermore, our visual judgment of the iGM images suggested a potentially higher agreement between this image-based metric and the perceived DOI. Haze was evaluated based on the Michelson contrast between inside and outside zones of the source aperture image. For mid to high gloss samples, this new metric correlated well with the standardized evaluation method for haze. Furthermore, a better representation for haze was obtained for low gloss samples. The DOI and haze were determined parallel and perpendicular to the plane of incidence of the instrument. The opportunity of such a 2D evaluation was illustrated on a sample featuring a pronounced directionality. Finally, the contrast attribute was introduced into the iGM. Despite the considerable impact of contrast on perceived gloss, mentioned in numerous scientific studies,^2,5,40,52,53 its evaluation is new to the field of industrial gloss meters. The proposed metric, based on the psychometric contrast between the peak of the specular reflection and the sample luminance, effectively distinguished samples with different lightness and gloss. In summary, the presented results illustrate the capabilities of the iGM instrument and the opportunities of image-based metrics to capture a more profound evaluation of gloss within a single instrument.

This study was however limited to the investigation of some specific processing algorithms. Future work should assess the various alternatives that were summarized in this work and select the most performant ones for each of the required gloss attributes. In addition, only the green channel of the color CMOS sensor has been used. The RGB color sensor and 0°:60° geometry however permit to estimate the color of samples, which is another attribute of visual appearance. A critical design parameter of the iGM will be the evaluation time, as it is typically higher than classical specular gloss meters. It could be reduced by increasing the light source levels to reduce the sensor exposure time or by obsoleting dark signal measurement images. Finally, the iGM cannot capture detailed image information of the sample surface, which is required for the evaluation of the surface-uniformity gloss attribute. This required future extension of the iGM and its processing methods could be based on the instrument proposed by Leloup et al. featuring a surface-focused camera sensor.³⁹