Introduction

As per the 2003 demographic statistics, the province of Ontario (Canada) is burdened with almost $9.6 billion in health and environmental damages each year because of smog pollution (Yap et al. 2005). Ground-level ozone, the principal element of photochemical smog, is a complex secondary photochemical pollutant formed by the chemical reactions in the air. It is well known as one of the major pollutants that degrades air quality (Van Eijkeren et al. 2002; Abdul-Wahab et al. 2005). The complex mechanism of ozone formation makes it even more complex and difficult to control. Although naturally occurring stratospheric ozone protects the earth from harmful ultraviolet radiation, the unhealthy level of ground-level ozone concentration plays a key role in producing human health injury and poses damaging effects to vegetation and material (Kim and Kumar 2005). Inhalation of ozone can trigger a number of health problems: irritation in the respiratory tract and eyes, chest tightness, coughing, wheezing; an even worse situation of people with pre-existing respiratory disorders, bronchitis, emphysema, and asthma. Children exposed to the outdoors during summer are mostly at risk when ozone concentration in the air remains higher. Besides, ozone is also responsible for the loss in agricultural production; in Ontario, air pollution causes loss of approximately $280 million due to loss of agricultural and forest productivity each year (Ontario Ministry of Environment 2004).

The complexity of the nonlinear nature of photochemical reaction of ozone formation is further aggravated by the wide-scale temporal and spatial variation of the meteorology and chemical processes that take place in between them. Faster chemical reactions strongly depend on the local atmospheric situation and directly affect local air quality. Slower reactions, on the other hand, have a great impact over wider regional or global spatial scale (Abdul-Wahab et al. 2005). The later is particularly much appropriate for the province of Ontario, especially in the southern Ontario because of the major contribution of neighboring US states emission sources to the province’s air quality. It is well documented (Yap et al. 2005) that the elevated level of ground-level ozone and particulate matters are associated with distinct weather patterns which affect the air quality in the lower Great Lakes Region. These weather conditions are strongly linked with slow-moving high-pressure systems at south of the lower Great Lakes resulting in long-range transport of the smog pollutants from neighboring industrial and highly urbanized cities of the Mid-Western US and Ohio Valley regions during warm south to southwesterly flow condition. However, the adverse effects of this transboundary air pollution is largely concentrated on southwestern Ontario, whereas the pollutants originated within Ontario have high impact in south central Ontario, i.e., Greater Toronto Area and other major population centers of Golden Horseshoe which accounts to the 61% of the total damages within the region (Yap et al. 2005).

So a modern, accurate, and reliable air pollution forecast can play a significant role in providing better warning system to protect human health. The complex relationship between the meteorology and the ground-level ozone concentration has been well documented by many authors, and attempts to develop a satisfactory ground-level ozone forecasting model have been numerous (Derwent et al. 1998; O’Hare and Wilby 1995; Abdul-Wahab et al. 2005). But model selection has always been problematic because of the need of a suitable model which can satisfactorily map the complex nonlinear relationship between the pollutant and the predictor meteorological variables. The major objective of this paper is to compare three dynamic nonlinear neural network models with widely accepted multilayer perceptron (MLP) model to forecast the ground-level ozone concentration in Hamilton, Ontario, Canada.

Presently, multilayer perceptron model has been accepted and proved to be a better model in capturing the nonlinearity of the air pollution variables and meteorology. A more elaborate literature review of different deterministic models and statistical models used in ozone forecasting have been presented in the project report funded by the European Community under the “Information Society Technology” program (Schlink et al. 2001). In spite of its drawbacks of interpretation, neural network model was included as one of the main tasks in that project because of its flexibility and capacity to model the nonlinear behavior of complex atmospheric phenomena. Several authors and researchers have compared MLP with linear regression models (Yi and Prybutok 1996; Comrie 1997; Gardner and Dorling 2000; Bordignon et al. 2002) and found it to be superior than the regression models in quantifying the nonlinearity and interactions between predictor–predictand variables and to modeling the hourly surface ozone concentrations. Agirre-Basurko et al. (2006) presented a comparison between two MLP based models and one multiple linear regression model to forecast hourly ozone and nitrogen oxide level in Bilbao (Spain) using traffic variables, meteorological variables, and ozone and NO2 data as input variables. The model results were compared with persistence of levels and the observed values. The performance of MLP, as expected, is found better than the multiple linear regression models. Schlink et al. (2006) attempted to link two key aspects of ground-level ozone problem: assessment of health effects and forecasting using 15 different statistical models in an intercomparison study in ten European regions. Their study (Schlink et al. 2006; Schlink et al. 2003) recommended that, in operational air pollution forecasting, neural networks and generalized additive models have the capacity to handle the strong nonlinear associations between the atmospheric variables. Sousa et al. (2007) used O3, NO, NO2, temperature, wind velocity, and relative humidity as inputs to develop principal component-based feed-forward artificial neural network (ANN) model to forecast 1 day ahead hourly ozone concentrations in an attempt to reduce the model complexity in terms of number of inputs. But unfortunately, the results obtained using the principal components were similar as that using the raw input data. Brunelli et al. (2007) applied recurrent neural networks for 2 days ahead forecasting of daily maximum O3 concentrations for Palermo city in Italy using wind direction, wind speed, barometric pressure, and ambient temperature. More recently, Chattopadhyay and Chattopadhyay-Bandyopadhyay (2008) used nonmeteorological predictors such as day and month along with the current concentration of total ozone using artificial neural network, multiple linear regression, and persistence forecast models to predict daily ozone concentration over Arosa, Switzerland and found better forecast results of ANN models than the statistical approaches. Stathopoulou et al. (2008) applied a back propagation algorithm-based neural network approach to investigate the influence of temperature on tropospheric ozone concentrations in urban and photochemically polluted areas in the greater Athens region. The results specified temperature as a predominant parameter to have a considerable affect on ozone concentrations.

However, neural network has its own disadvantages too. It has been unable to reveal the cause–effect interactions of the phenomena which, as suggested by Kolehmanien et al. (1999), can be possible to overcome by introducing different types of neural networks together and by analyzing the characteristic behavior of the data prior to forecasting (Schlink et al. 2003). In this paper, three dynamically different neural network models, namely standard multilayer perceptron, time-lagged feed-forward network (TLFN), fully recurrent neural networks (RNN), and Bayesian neural network (BNN) models are investigated to identify the best model for ground-level ozone forecasting in Hamilton region.

Methodology

Neural network models

Artificial neural network models are proved to be very powerful and efficient methods for dealing with complex problems of associations, classification, and prediction (Ordieres et al. 2005). A neural network can be characterized by its architecture, presented by the network topology and pattern of connections between nodes, its method of determining the connection weights, and the activation functions that it employs (Dibike and Coulibaly 2006). Multilayer perceptrons constitute probably the most widely used network architecture and has got wide application in atmospheric science (Gardner and Dorling 2000; Ordieres et al. 2005). They are composed of a hierarchy of processing units organized in a series of two or more mutually exclusive sets of neurons or layers. The information flow in the network is restricted to a flow, layer by layer, from the input to the output, hence also called feed-forward network. However, in temporal problems, measurements from physical systems are no longer an independent set of input samples but functions of time. To exploit the time series structure in the inputs, the neural network must have access to this time dimension (Dibike and Coulibaly 2006). While feed-forward neural networks are popular in many application areas, they are not well suited for temporal sequences processing due to the lack of time delay and/or feedback connections necessary to provide a dynamic model. They can be used as pseudo-dynamic models only by using successively lagging multiple inputs based on correlation and mutual information analysis of the input data. There are however various types of neural networks that have internal memory structures which can store the past values of input variables through time, and there are different ways of introducing “memory” in a neural network in order to develop a temporal neural network. Time-lagged feed-forward and recurrent networks are two major groups of dynamic neural networks mostly used in time series forecasting (Coulibaly et al. 2001a, b; Dibike and Coulibaly 2006).

Time-lagged feed-forward neural network is an extension of the standard MLP models which can be formulated by replacing the neurons in the input layer of an MLP with a memory structure, known as tap delay line or time delay line. The size of the memory structure (tap delay line) depends on the number of past samples that are needed to describe the input characteristics in time, and it has to be determined on a case-by-case basis. TLFN uses delay-line processing elements, which implement memory by simply holding past samples of the input signal shown in Fig. 1 (without the feedback connection). The output of such a network with one hidden layer is given by (Dibike and Coulibaly 2006):

$$y\left( n \right) = \phi _1 \left( {\sum\limits_{j = 1}^m {w_j y_j \left( n \right) + b_o } } \right)$$
(1)
$$= \phi _1 \left\{ {\sum\limits_{j = 1}^m {w_j \phi _2 \left[ {\sum\limits_{l = 0}^k {w_{jl} x(n - 1) + b_j } } \right] + b_o } } \right\}$$
(2)

where m is the size of the hidden layer, n is the time step, w j is the weight vector for the connection between the hidden and output layers, w jl is the weight matrix for the connection between the input and hidden layers, ϕ 1 and ϕ 2 are transfer functions at the output and hidden layers, respectively, and b j and b o are additional network parameters (biases) to be determined during training of the networks with observed input/output data sets. For the case of multiple inputs (of size p), the tap delay line with memory depth k can be represented by:

$$X\left( n \right) = \left[ {x\left( n \right),x\left( {n - 1} \right),....,x\left( {n - k + 1} \right)} \right]$$
(3)
$$X\left( n \right) = \left( {x_1 \left( n \right),x_2 \left( n \right),........,x_p \left( n \right)} \right),$$
(4)

where x(n) represents the input pattern at time step n, x j (n) is an individual input at the nth time step, and X(n) is the combined input to the processing elements at time step n. Such a delay line only “remembers” k samples in the past. An interesting attribute of the TLFN is that the tap delay line at the input does not have any free parameters; therefore, the network can still be trained with the classical back propagation algorithm. The TLFN topology has been effectively used in nonlinear system identification, time series prediction (Coulibaly et al. 2001b), temporal pattern recognition, and parallel hybrid modeling.

Fig. 1
figure 1

Standard MLP (without time delay line and feedback connection), TLFN (without feedback connection), and RNN (with feedback connection) model structure (Coulibaly et al. 2001b)

Full size image

The recurrent neural network model used in this work is the basic Elman type RNN (Elman 1990) and also known as the globally connected RNN. The network consists of four layers: the input layer, the hidden layer, the context unit, each with n number of nodes and the output layer with one node. Each input unit is connected with every hidden unit, as is each context unit. Conversely, there are one-by-one downward connections between the hidden nodes and the context units leading to an equal number of hidden and contest units. In fact, the downward connections allow the context units to store the outputs of the hidden nodes (i.e., internal states) at each time step; then the fully distributed upward links feed them back as additional inputs. Therefore, the recurrent connections allow the hidden units to recycle the information over multiple time steps and thereby to discover temporal information contained in the sequential input and relevant to the target function (Coulibaly et al. 2001b). Thus, the RNN has an inherent dynamic (or adaptive) memory provided by the context units in its recurrent connections. The output of the network depends not only on the connection weights and the current input signal but also on the previous states of the network, which can be shown by the following equations (Coulibaly et al. 2001b):

$$y_j = Ax\prime \left( t \right)$$
(5)
$$x\prime {\left( t \right)} = G{\left\lfloor {W_{h} x\prime {\left( {t - 1} \right)} + W_{{h_{o} }} x{\left( {t - 1} \right)}} \right\rfloor }$$
(6)

Where x′(t) is the output of the hidden layer at time t given an input vector x(t), G( ) denotes a logistic function characterizing the hidden nodes, the matrix W h represents the weights of the h hidden nodes that are connected to the context units, W ho is the weight matrix of the hidden units connected to the input nodes, y j is the output of the RNN assuming a linear output node j, and A represents the weight matrix of the output layer neurons connected to the hidden neurons. The Elman-style RNN is a state-space model since Eq. 6 performs the static estimation and Eq. 5 performs the evaluation (Coulibaly et al. 2001b).

According to Coulibaly et al. (2001b), a major difficulty, however, with RNN is the training complexity because the computation of ▿E(W), the gradient of the error E with respect to the weights, is not trivial since the error is not defined at a fixed point but rather is a function of the network temporal behavior. Here, in order to identify the optimal training method and to reduce computing time, each model has been trained with a different algorithm using the same delayed inputs. Finally, the delta-bar-delta algorithm was selected after investigating several other methods. Delta-bar-delta algorithm is an improved version of the back-propagation algorithm. Unlike standard back-propagation, delta-bar-delta algorithm uses a learning method where each weight has its own self-adapting coefficient. It does not use the momentum factor of the standard BP network. The essence of the rule is that past calculated error values for each weight are used to infer future calculated error values; hence, by knowing the probable errors, the system takes “intelligent” steps in adjusting the weights. Furthermore, each connection weight has its individual learning rate which varies over time based on the current error information found with standard back-propagation; hence, more degree of freedom is achieved which reduced the convergence time (NeuroSolutions 2004).

Bayesian neural network model

The Bayesian neural network model used in this work was developed by Khan and Coulibaly (2006). Bayesian approach implements the conventional or standard learning process; but instead of single set of weights, it considers a probability distribution of weights. According to Khan and Coulibaly (2006), the process starts with a suitable prior distribution, p(w), for the network parameters (weight and biases). Once the data D is observed, Bayes’ theorem is used for deriving an expression of the posterior probability distribution for the weights, p(w|D), as follows:

$$p\left( {w|D} \right) = \frac{{p\left( {D{\text{ $|$ }}w} \right)p\left( w \right)}}{{p\left( D \right)}}$$
(7)

where, p(D|w) is the dataset likelihood function and the denominator, p(D) is a normalizing factor, which can be obtained by integrating over the weight space as follows:

$$p\left( D \right) = \int {p\left( {D{\text{ $|$ }}w} \right)p\left( w \right)dw{\text{ }}} $$
(8)

The left-hand side of Eq. 7 gives unity when integrated over all weight space. Once the posterior has been calculated, every type of inference is made by integrating over that distribution. Therefore, in implementing Bayesian method, expressions for the posterior distribution, p(w), and the likelihood function, p(D|w), are needed. The prior distribution, p(w), which is not related with data, can be expressed in terms of weight-decay regularizer, \(Ew = \frac{1}{2}\sum\limits_{i = 1}^w {wi^2 } \), where W is the total number of weights and biases in the network. Similarly, the likelihood function in Bayes’ theorem 1, which is dependent on data, can be expressed in terms of error function, \(ED = \frac{1}{2}\sum\limits_{n = 1}^N {\left( {y^n \left( {x^n ;w} \right) - t^n } \right)^2 } \), where, x is the input vector, t is the target value, and y(x;w) is the network output. Upon deriving the expressions for the prior and likelihood functions and using those expressions in Eq. 7, the posterior distribution of weights can be obtained. The objective function in the Bayesian method corresponds to the inference of the posterior distribution of the network parameters. After defining the posterior distribution (objective function), the network is trained with a suitable optimization algorithm to maximize the posterior distribution p(w|D). Thus the most probable value for the weight vector w MP corresponds to the maximum of the posterior probability. Using the rules of conditional probability, the distribution of outputs for a given input vector, x, can be written in the form

$$p\left( {t|x,D} \right) = \int {p\left( {t{\text{ $|$ }}x{\text{,}}w} \right)p\left( {w{\text{ $|$ }}D} \right)dw{\text{ }}} $$
(9)

where p(t x,w) is simply the model for the distribution of noise on the target data for a fixed value of the weight vector w MP, and p(w|D) is the posterior distribution of weights. The posterior distribution over network weights provides a distribution about the outputs of the network. If a single-valued prediction is needed, the mean of the distribution is used, and while the uncertainty about the prediction is needed, the full predictive distribution is used to present the range of uncertainty about the prediction. A more detailed description of BNN approach as used herein can be found in Khan and Coulibaly (2006).

Study area and database

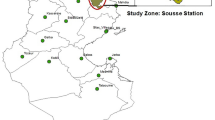
The database used in this study is collected from the air quality network of the Ministry of Environment, Ontario (Fig. 2). The dataset comprises hourly average ground-level ozone concentrations collected from three air quality monitoring stations of Hamilton, located in southern Ontario. Of these three stations, the station in Hamilton Downtown (43°15′30″ N, 79°51′41″ W) is located in a densely populated residential area and intense vehicular traffic. The most direct influence of the elevated level of ozone at that station is believed to be generated from the adjacent Wilson Avenue, a heavily traveled one-way street at about 30 m south of the site. The nearest heavy industry to the site is located 2.5 km northeast. The station in Hamilton Mountain (43°13′47″ N, 79°51′43″ W) is also situated within a residential area near a school. The third station, Hamilton West (43°15′31″ N, 79°54′09″ W), situated near the Main Street West and Highway 403, is mainly affected by heavy vehicular traffic at Highway 403. These two stations are not very much affected by heavy industries, as there is no industry within the 5 km band of the sites. The database initially had hourly ozone values during 1990–2004 which were further reduced to bihourly concentrations to reduce modeling time.

Fig. 2
figure 2

Ozone and meteorological sites in Hamilton (partial source: http://atlas.nrcan.gc.ca)

Full size image

For meteorological variables, three weather stations located near the monitoring sites (Fig. 2) were considered initially. These stations are located at Hamilton Airport (43°10′ N, 79°55′ W), Burlington Piers (43°18′ N, 79°48′ W), and Royal Botanical Garden (RBG; 43°17′ N, 79°54′ W). The database for the Hamilton Airport was available from 1990 which is still under full operation. The second station in Burlington had data available from 1994; however, the RBG site started operating only from 2000, and its inclusion in the modeling did not improve the result much. So finally, the RBG station was not included in the further analysis. The meteorological variables considered were collected from the Ontario Climate Centre of Environment Canada. Based on earlier works (Gardner and Dorling 2000; Agirre-Basurko et al. 2006; Schlink et al. 2006), the most important meteorological variables for ground-level ozone include solar radiation, maximum temperature, wind speed, wind direction, relative humidity, dry bulb temperature, vapor pressure, etc. But the successful use of these variables is strongly dependent on the availability of good quality data. For this specific work, it would have been ideal to use maximum temperature and solar radiation data as they are very good indicators of the smog formation (Gardner and Dorling 2000). Unfortunately, these data were not available in any of the weather stations located near the three selected air quality monitoring network stations. The vapor pressure variable also could not be used because of low quality data with large amount of missing values. So finally, only four variables: wind speed (km/hr), wind direction (tens of degrees), dry bulb temperature (0.1°C), and relative humidity (%) data were used as input variables with the assumption that they might be able to capture the real chemistry of ozone pollution. Like ozone, the meteorological variables were also collected on an hourly basis during 1994–2004 and were reduced to bihourly values for this study.

The missing values in both pollutant and meteorological database were computed to provide a complete database. For months with missing data for more than 10 days, the entire month was removed from the analysis. For example, because of incomplete data months, March to May in the year 2002 was excluded. For short gaps (up to 4 h), the missing values were filled with linear interpolation, while medium gaps (4 to 8 h) and larger gaps (more than 8 h) were computed using multivariate partial least square technique based on nearby station values.

Descriptive statistics of the ozone variables are shown in Table 1, while Fig. 2 shows the location of the pollutant and meteorological variable monitoring stations within the city area.

Table 1 Ground-level ozone statistics
Full size table

Model design

A typical neural network topology is problem dependent; hence, whatever the type of neural network (NN) model is considered, it is necessary to determine the appropriate network architecture (i.e., number of inputs, hidden and output nodes) in order to achieve satisfactory generalization capability (Coulibaly et al. 2001a). Except the BNN model, all other ANN models used in the study are developed using the NeuroSolutions v4 (NeuroDimension Inc., Gainesville, FL, USA). In this particular work, ground-level ozone concentrations during 1994 to 2004 have been used to develop neural network models. Because of over 6 months of missing value, the year 1997 has not been included. From the 10 years of observed data from 1994 to 2004, first 5 years (1994–1996, 1998–1999) are considered for constructing the models, 1 year data (2000) for cross-validation, and remaining 4 years (2001–2004) of dataset were used for testing the models.

Selection of predictors

In case of both the neural network models and the Bayesian neural network model, the selection of most important and relevant predictors is the most vital task in the modeling process. For this work, the predictors were selected based on linear autocorrelation and partial autocorrelation analysis and nonlinear sensitivity analysis. At first, correlation between the historical values of each predictor and predictand was examined to get an initial idea about the important time lags. Then, the partial autocorrelation (PACF) analysis was performed for each of the input and output variables to identify range of significant lags. From the analysis, it was found that time lags up to 14 were approximately important. So for all variables, lags from 1 to 14 were selected for sensitivity analysis using a TLFN model which is the final stage of screening input variables. The sensitivity analysis is a measure of the relative importance among the predictors (inputs of the neural network) which calculates the variation of the output variables with the variation of inputs. The basic idea is, the changes in the outputs even with a slight change in input variables are calculated. Each input is varied ±n times its standard deviation while keeping others fixed about their mean, and the network output is calculated for a specific number of steps above and below the mean. The neural network measures the relative sensitivity which is the ratio between the standard deviation of the output and the standard deviation of the input, which, as a result, gives the relative importance of each input (Dibike and Coulibaly 2006). The important lags selected by sensitivity analysis for all three stations are shown in Table 2. The number of input variables in three stations varied; Hamilton Downtown has highest 29 variables followed by Hamilton Mountain with 27 variables. The number of variables in Hamilton West was 24.

Table 2 Selected lags for all stations
Full size table

Model setup

Selection of an appropriate architecture of any neural network model is a prerequisite behind its successful use since the structure directly influences the computational complexity and generalization capability of a model. A more complex than necessary model can over-train the model, while a too-simple model with fewer numbers of nodes than necessary may not be able to learn data successfully (Coulibaly et al. 2001b). Because of absence of a standard methodology of selecting an appropriate network, a trial-and-error procedure has been applied to get the optimal model parameters.

For each station, same input variables were used for all four models in order to compare model performance. Except BNN, the comparison of MLP, TLFN, and RNN model performance parameters are similar. In this study, trial-and-error approach was carried out with the screened variables by varying model parameters, and the best ones were selected by comparing model performance until the optimum network was achieved.

In BNN model design, a two-layer MLP network is used with the same set of input. The BNN network consists of one hidden layer, with tangent hyperbolic activation function and one output layer with linear processing unit. The parameters on BNN model, which runs in the MatLab environment, are quite different. Unlike other ANN models, the initialization of parameters in BNN is performed using a distribution of parameters. The optimal model parameters for all three stations using four models are shown in Tables 3 and 4.

Table 3 Optimal MLP, TLFN and BNN model parameters
Full size table
Table 4 Optimal BNN model parameters
Full size table

Evaluating model performance

Many model performance statistics are available in order to assess the accuracy of the estimates. For this particular work, the model performance and forecasting results were compared by a set of five statistics. A brief description of these statistics is given below:

The root mean square error (RMSE) is the square root of the differences between the observations and predicted values. The mean square errors provide a general illustration of the relevancy of the simulated values by giving a global goodness to fit by including errors and biases in the calculation. The lower the RMSE value, the better the model. RMSE, however, does not necessarily reflect whether the two sets of data move in the same direction. For instance, by simply scaling the network output, we can change the MSE without changing the directionality of the data. This limitation can be overcome by introducing a second index, correlation coefficient, r.

The correlation coefficient (r) between an observed value and a desired model output provides a measure of the prediction ability of a model, and it is an important tool for comparing two models as it is independent of the scale of data. The r value can range from −1 (perfect negative correlation) to 1 (perfect positive correlation) through 0, where 0 means no correlation. An r value of 0.9 and above is very satisfactory, 0.8 to 0.9 presents a fairly good model, but below 0.7 is considered unsatisfactory.

The coefficient of determination (R 2) which is simply the square of the coefficient of correlation assesses the strength of an association between two variables. It is also a measure of the ability of a model to predict the concentrations, which are different from mean. Moreover, it provides a useful comparison between the models since it is independent of the scale of data. It lies between zero and unity; the closer to unity, the greater the explanatory power.

The normalized mean squared error (NMSE) is another version of the mean square error which is normalized with the object of establishing comparisons among different models (Agirre-Basurko et al. 2006).

The mean absolute error (MAE) is a linear score which means that all the individual differences are weighted equally in the average. In short, it measures the average magnitude of the errors in predicted dataset without considering their direction. MAE ranges from 0 to infinity, where 0 corresponds to the ideal condition which in particular permits to compare the appropriateness of using the models.

Forecasting results

The forecasting results of the ozone concentrations are evaluated based on the testing results for the period of 2001–2004. A comparison of MLP, TLFN, BNN, and RNN model forecasting performance statistics for Hamilton Downtown is summarized in Table 5. The best forecasting results should have the RMSE, NMSE, and MAE values equal to zero and r and R 2 value equal to unity. Firstly, the results up to t + 1 and t + 2 time steps ahead show similar result for all three stations. Overall, the TLFN model resulted in lower RMSE, r, R 2 and MAE values than the other three models. The performance of RNN, BNN, and MLP model is quite similar in terms of r and R 2 values, while the RMSE and MAE results showed that RNN is slightly superior to the static MLP model. The NMSE values obtained shows a bit different result with lowest NMSE value for BNN model. Overall, all models have showed similar performances; TLFN and RNN had coefficient of correlation r (0.91–0.93) values slightly higher than 0.90 compared to BNN and MLP (0.89–0.92) models for one-step ahead forecasting and R 2 values higher than 0.80, which clearly demonstrates the efficiency of the models for 2-h ahead forecasting. The r value for the forecasting period (i.e. 4 h ahead) t + 2 is also satisfactory.

Table 5 Model forecasting statistics
Full size table

Unlike the forecasting results of first two periods, the three- to five-step ahead forecasting results demonstrate slightly better performances of RNN model over TLFN and other models. The lowest RMSE, NMSE, and MAE values were obtained by the RNN model for downtown station and mountain station. In case of Hamilton Mountain, TLFN showed lower errors than other three models. The greatest values of coefficient of correlation r were also obtained for RNN model which clearly shows that RNN model worked better than other models during this time frame. A very important observation regarding the forecasting results is: all models showed variation in their performances up to six-step ahead forecasting which indicates their ability to model up to 12 h ahead (t + 6); the values beyond this point, however, remained the same. Figure 3 represents a comparative view of the forecasting results of Hamilton Downtown and Hamilton Mountain station in terms of RMSE and R 2 values. The graphs show the more accurate performances of TLFN and RNN models than static MLP and BNN models. These results suggest that the inclusion of time delay in TLFN and/or adaptive memory (context unit) in RNN have the capacity to improve the model forecasting skill as compared to conventional static neural network (MLP in this case).

Fig. 3
figure 3

Comparison of model forecasting performance statistics for a Hamilton Downtown and b Hamilton Mountain stations

Full size image

To further assess the model performance in general, scatter plots between the observed and the predicted concentrations were plotted. Figures 4, 5, and 6 show the scatter plots of t + 1, t + 4, and t + 6 forecasting period in Hamilton Downtown area. In case of one-step ahead forecasting, the MLP and BNN models diverge significantly from the 45° line and tended to shift towards right. TLFN and RNN model during this time period also shifted but is still closer to the ideal line. These patterns clearly indicate that both RNN and TLFN model performed more accurately than conventional MLP model. Thus, adding an input delay memory or a context unit to the static MLP can be a good alternative to improve the forecasting accuracy. The forecasting results of t + 4 (8 h ahead) and t + 6 (12 h ahead) showed similar pattern deteriorating consistently with increasing forecasting time. The scatter plots also indicate that these models have limitation in capturing higher and lower concentrations. BNN and MLP models have been totally unable to predict higher values which are more visible in Figs. 5 and 6. In case of low concentrations, predicted values by RNN are relatively better with MLP performing inferior to other two models. Even though the extremely higher and lower values are due to extreme conditions, RNN appears to be more capable of capturing those underlying extreme phenomena. This clearly suggests that the temporal representation capability of global RNN model is better than the static MLP model and slightly better than the TLFN model.

Fig. 4
figure 4

Scatter plots of the observed and predicted ozone concentrations for one-step (2-h) ahead forecasting

Full size image
Fig. 5
figure 5

Scatter plots of the observed and predicted ozone concentrations for four-step (8-h) ahead forecasting

Full size image
Fig. 6
figure 6

Scatter plots of the observed and predicted ozone concentrations up to six-step (12-h) ahead forecasting

Full size image

The performance of BNN model is not superior to other neural network model; yet, the performance statistics indicates that they can be a good alternative for short-term forecasting (up to 4 h ). Moreover, the complexity of BNN model is simpler than the NN models in terms of the number of neurons. The reason behind this simple-yet-better performance of BNN model may be due to the consideration of parameter uncertainty in the form of probability distributions of weights and biases and finding the outputs of the networks by integrating over the weight space of posterior probability distribution instead of using single “best set” of weights as in the case of conventional MLP model. This parameter uncertainty consideration and the high computational capability of the nonlinear processing unit increases the capacity of BNN model to out-perform the widely used MLP model. Keeping in mind the higher ozone problems during summer period, the performances of the models are calculated with 95% confidence interval using the BNN model for 2 and 4-h ahead forecasting period. Figures 7 and 8 present the confidence interval plots for 2-h (t + 1) and 4-h (t + 2) ahead time period for mid-July to mid-Aug, 2004. The uncertainty bands created by the 2-h ahead BNN model hold both the observed and other modeled values quite well. Except a few deviations, the BNN model band for 4-h ahead forecasting has also been able to hold both the observed and predicted values. But the gradually increasing uncertainty band indicates the degradation of model performance compared to the previous time step. The fact that TLFN, RNN, and MLP modeled values fall within the prediction band of BNN indicates that it can be a reliable tool where uncertainty estimate is of particular concern.

Fig. 7
figure 7

Comparative results of 2-h ahead ozone forecasting with 95% confidence interval: Hamilton Downtown (site # 29000)

Full size image
Fig. 8
figure 8

Comparative results of 4-h ahead ozone forecasting with 95% confidence interval: Hamilton Downtown (site # 29000)

Full size image

Although the models in this work proved efficient in short- term forecasting, the disadvantages should not be ignored. Successful application of BNN and ANN models are completely dependent on the quality and quantity of data, the selection of suitable prior and noise models, and the predictive distribution of outputs. Another major limitation of neural network models is their inability to interpret underlying physical processes. Thus, these models cannot replace the physical models, yet they can be a good alternative in cases where prediction accuracy and estimation of uncertainty are of concern.

Conclusion

This study presents an informative comparison of the dynamic neural networks and static MLP model within the context of short term ground-level ozone forecasting in Hamilton, Ontario, Canada. A secondary objective was to assess the applicability of Bayesian neural network in ozone forecasting. Comparison of the four model performances reveals that all the models demonstrate significant improvement in prediction accuracy over static MLP model. In particular, the time-lagged feed-forward model and recurrent neural network models have proved to be more efficient than other two models in capturing the future air quality conditions. The analysis further shows that all these four models can forecast effectively up to 12 h. For one (2-h) and two (4-h) step ahead forecast, the results indicate that MLP is less accurate compared to BNN model. In general, it was clear that, although the overall performances of these models were satisfactory, none of them was able to predict with accuracy the low and extremely high levels of concentrations. This may be due to the fewer number of extreme values in the training sample. The BNN model performance shows that it has been able to achieve similar performances as other models with much less complex network in terms of the number of neurons in the network. It can also be a good alternative where model prediction confidence limits are of particular concern. One disadvantage of BNN model, however, is the higher complexity of BNN learning algorithm than the dynamic neural network models. But one exceptional advantage of BNN model is its ability to provide predictions along with the precision of the outputs in the form of error bars or confidence intervals without losing model prediction accuracy as compared to other NN models. However, the major limitations of the neural network model should not be ignored. Its inability to interpret the underlying physical processes is the major barrier to its sole use in predicting air quality; rather, it can be a good supportive tool with standard process-based models.