Skip to main content
SpringerLink
Log in

New chaotic image encryption algorithm based on cross-mapping

  • Published:
Wuhan University Journal of Natural Sciences

Abstract

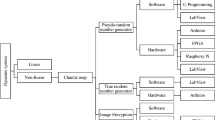
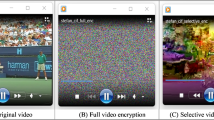
Chaotic cryptography has been applied to image encryption; however, only the traditional low-dimensional chaotic systems has been widely analyzed or deciphered, which does not show satisfied security and efficiency. To solve this problem, a new algorithm based on cross-chaos map has been created in this article. The image pixels are scrambled under control of high-dimensional chaotic sequence, which is generated by cross chaotic map. The image pixels are substituted by ciphertext feedback algorithm. It can relate encryption required parameters with plaintext and can make a plaintext byte affect more ciphertext bytes. Proved by theoretical analysis and experimental results, the algorithm has higher complex degree and has passed SP800-22 pseudo-random number standard tests, and it has high encryption speed, high security, etc. It can be widely applied in the field of image encryption.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Wang Xingyuan. Chaos in the Complex Nonlinear Systems [M]. Beijing: Publishing House of Electronics Industry, 2003 (Ch).

    Google Scholar 

  2. Palmaore J. Computer Arithmetic, Chaos and Fractals [J]. Physica, 2006, 42: 99–110.

    Google Scholar 

  3. Jakimoski G, Kocarev L. Analysis of some recently proposed chaos-based encryption algorithms [J]. Physics Letters A, 2001, 291(6): 381–384.

    Article  MathSciNet  MATH  Google Scholar 

  4. Zhang L H, Zhang Y F. Research on Lorenz chaotic stream cipher [C]//VLSI Design and Video Technology 2005 Proceedings of IEEE International workshop. New York: IEEE Press, 2005: 431–434.

    Google Scholar 

  5. Wang Lei. Research of one-way hash function based on Logistic map [J]. Computer Engineering and Design, 2006, 27(5): 774–776 (Ch).

    Google Scholar 

  6. Wang Yong, Wong K W, Liao Xiaofeng, et al. A new chaos-based fast image encryption [J]. Software Applications, 2011, 11(1): 514–522.

    Google Scholar 

  7. Xiao D, Liao X F, Wei P C. Analysis and improvement of a chaos-based image encryption algorithm [J]. Chaos, Solitons & Fractals, 2009, 40(5): 2191–2199.

    Article  MathSciNet  MATH  Google Scholar 

  8. Wang Y, Liao X F, Xiang T. Cryptanalysis and improvement on a block cryptosystem based on iteration a chaotic map [J]. Physics Letters A, 2007, 363: 277–281.

    Article  MATH  Google Scholar 

  9. Alvarez E, Femandez, Gacria P, et al. New Approach to Chaotic Encryption [J]. Physics Letters A, 1999, 263(4–6): 373–375.

    Article  Google Scholar 

  10. Bpatista M S. Cryptography with chaos [J]. Physics Letter A, 1998, 240(l–2): 50–54.

    Article  Google Scholar 

  11. Wang Y F, Shen H B, Yan X L. Output cryptograph mixed feedback chaos stream cipher design [J]. Journal of Zhejiang University, 2006, 11(40): 31–37.

    Google Scholar 

  12. Liu Jialing, Zhang Hong, Wang Yong. Analysis and improvement on a class of iterative chaotic block cipher [J]. Computer science, 2008, 16(135): 141–144 (Ch).

    Google Scholar 

  13. Klapper A. The vulnerability of geometric sequences based on fields of odd characteristic [J]. Journal of Cryptology, 1994, 7: 33–52.

    Article  MathSciNet  MATH  Google Scholar 

  14. Wong W K, Lee L P, Wong K W. An improved chaotic encryption method [J]. Computer Physics Communications, 2001, 138(3): 234–236.

    Article  MathSciNet  MATH  Google Scholar 

  15. Ren Hong’e, Shang Zhenwei, Zhang Jian. Image encryption algorithm based on new two-dimensional map for rectangular image [J]. Optical and Precision Engineering, 2008, 16(8): 1483–1489 (Ch).

    Google Scholar 

  16. Zhang Q, Guo L, Wei X P. Image encryption using DNA addition combining with chaotic maps [J]. Mathematical and Computer Modelling, 2010, 52: 2028–2035.

    Article  MathSciNet  MATH  Google Scholar 

  17. Liao X F, Lai S Y, Zhou Q. A novel image encryption algorithm based on self-adaptive wave transmission [J]. Signal Processing, 2010, 90: 2714–2722.

    Article  MATH  Google Scholar 

  18. Han Fengying, Zhu Congxu. One kind based on double unidimensional chaos system picture encryption algorithm [J]. J Computer Engineering and Applications, 2007, 43(20): 50–51.

    Google Scholar 

  19. Lu Kan, Sun Jianjun, Huang Youlai, et al. Chaotic Dynamics [M]. Shanghai: Shanghai Translation Press, 1990(Ch).

    Google Scholar 

  20. Geisel T, Fairen V. Statistical properties of chaos in Chebyshev maps [J]. Physics Letters A, 1984, 105: 263–266.

    Article  MathSciNet  Google Scholar 

  21. NIST. SP800-22-1. A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications [S]. Gaithersburg: NIST, 2001.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Computer Science and Technology, Harbin Institute of Technology, Weihai, 264209, Shandong, China

    Xiaojun Tong, Yang Liu, Miao Zhang & Hongyu Shi

Authors
  1. Xiaojun Tong
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yang Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Miao Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Hongyu Shi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Xiaojun Tong.

Additional information

Foundation item: Supported by the National Natural Science Foundation of China (60973162), the Natural Science Foundation of Shandong Province of China (ZR2009GM037), the Science and Technology Project of Shandong Province, China (2010GGX10132, 2012GGX10110), the Key Natural Science Foundation of Shandong Province of China (Z2006G01), and the Soft Science Project of Shangdong Province of China (2012RKA10009)

Biography: TONG Xiaojun, female, Professor, research direction: chaos cryptography and information security.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Tong, X., Liu, Y., Zhang, M. et al. New chaotic image encryption algorithm based on cross-mapping. Wuhan Univ. J. Nat. Sci. 17, 461–467 (2012). https://doi.org/10.1007/s11859-012-0871-y

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11859-012-0871-y

Key words

CLC number

Search

Navigation