A Review on Applications of Chaotic Maps in Pseudo-Random Number Generators and Encryption

Abstract

Because of the COVID-19 pandemic, most of the tasks have shifted to an online platform. Sectors such as e-commerce, sensitive multi-media transfer, online banking have skyrocketed. Because of this, there is an urgent need to develop highly secure algorithms which can not be hacked into by unauthorized users. The method which is the backbone for building encryption algorithms is the pseudo-random number generator based on chaotic maps. Chaotic maps are mathematical functions that generate a highly arbitrary pattern based on the initial seed value. This manuscript gives a summary of how the chaotic maps are used to generate pseudo-random numbers and perform multimedia encryption. After carefully analyzing all the recent literature, we found that the lowest correlation coefficient was 0.00006, which was achieved by Ikeda chaotic map. The highest entropy was 7.999995 bits per byte using the quantum chaotic map. The lowest execution time observed was 0.23 seconds with the Zaslavsky chaotic map and the highest data rate was 15.367 Mbits per second using a hyperchaotic map. Chaotic map-based pseudo-random number generation can be utilized in multi-media encryption, video-game animations, digital marketing, chaotic system simulation, chaotic missile systems, and other applications.

1 Introduction

The COVID-19 pandemic has caused an exponential growth in the dependency on internet sources. Due to this, a majority of the transactions take place online, which makes online security for banking and e-commerce highly essential. Currently, there are multiple cryptographic algorithms that have been developed and have been effectively deployed. Random number generation is the backbone of every cryptographic algorithm [1]. Pseudo-random number generators are used in applications, such as digital signatures, hashing, encryption, seed vector, One-Time Passwords (OTP), etc. [2]. These pseudo-random number generators are also a type of deterministic generator where the output is dependent on the initial seed sequence and the design of a generator [3]. These numbers are not truly random because if the initial value is known, then the output can be completely predicted. There are two major categories of random number generators, hardware random number generator, and software seed-based random number generator [4]. In earlier times, random number generators were used in electronic video games. Later on, their applications were further expanded to simulators [5, 6]. Now, random number generators are also used for cryptographic applications [7]. Hardware random number generators generate numbers through a physical process, such as on the basis of thermal noise or other external factors [8]. These types of generators are useful when non-reversible random numbers have to be generated.

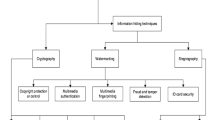
Figure 1 shows a hierarchical tree diagram of the recent developments in using chaotic maps in non-linear dynamic systems, such as, a pseudo-random number generator and an encryptor. Pseudo-random number generators can be found in both hardware and software. Most hardware implementations are done on FPGA, but there are some microcontroller-based hardware implementations as well, that use Arduino and Raspberry Pi. Encryption applications are mostly used for image ciphering [9], with very few exceptions for audio. The dotted lines represent that there are various other applications under linear dynamic systems and also under chaotic maps. But these applications represented by dotted lines are not covered in the scope of this paper.

Dynamic systems are the functions in mathematics that describe a point in geometrical space with the help of time [10]. The simplest example of a dynamic system could be a pendulum of a clock. A dynamic system has a state for a given time and can be represented using a vector mathematical function with an appropriate state-space model [11]. The evolution rule allows us to determine the next state of a dynamical system using the current state and its behavior. Most of the dynamic systems are deterministic [11], however, some systems generate stochastically random events, or their complete description is unavailable to us. A dynamic system can be completely modeled for predicting its future behavior by an analytical solution that is time dependant. Dynamic systems can be further classified into two types, namely, linear dynamic systems and non-linear dynamic systems [12]. A non-linear dynamic system is mathematically defined as a system whose output is not proportional to the changes made in the input. Linear dynamic systems are the dynamic systems whose evaluation is a linear function, i.e. changes in the output are linearly proportional to the changes in the input [13]. Chaotic systems are a type of non-linear dynamic systems. Chaotic maps are widely used in building pseudo-random number generators and in multimedia encryption.

The data science field is growing day by day and hence there is a need to protect the data. This data can be the personal information of the client or a sensor readout every second. It is important to use pseudo-random number generators which are chaotic, making it difficult for any pattern recognition algorithm to breakthrough. There are some reports on the use of random numbers in the data science field, for example, random projection scheme [14], random forest method [15], random sampling and random variables [16]. The chaotic function-based pseudo-random number generator is useful for avoiding data mining for unauthorized personnel [17, 18]. Pseudo-random number generators can also be used for encryption and decryption of IoT networks, increasing their security. [19].

Soliman et al. [14] has developed a random projection scheme to improve security in iris detection. The pseudo-random number generator using chaotic maps can be a seed point to generate random projections.

Fig. 1

Hierarchical tree diagram of recent trends in applications of chaotic maps in non-linear dynamic systems, such as, pseudo-random number generator and encryptor. Pseudo-random number generators are implemented in hardware and software. Most of the hardware implementation is done on FPGA but there are some microcontroller-based hardware implementations also namely, Arduino and Raspberry Pi. Encryption applications are majorly done for image ciphering and very few are done for audio

Fig. 2

Different chaotic maps used for the application of pseudo-random number generation and multimedia encryption

2 Chaotic Maps

Chaotic maps are a field of study of mathematics, where dynamic systems produce a random state which is absolutely disordered and appears irregular but is governed by the initial seed conditions. Chaos theory explains the relationship between totally appearing random chaotic outputs and underlying patterns that generate these outputs. These patterns can be analyzed well if the interconnection of a generator is known. These generators typically rely on a feedback loop, repeatability, self-similarity, and fractal behavior of the system. Figure 2 shows the different chaotic maps used for the application of pseudo-random number generation and multimedia encryption.

There are two types of chaotic maps namely, continuous and discrete. These chaotic maps can be complex or work with real numbers. Some chaotic maps can have up to four dimensions. Most of the chaotic maps reported in the literature are of three dimensions. Chaotic maps’ seed points can vary between 0 parameters up to 18 parameters. The most complex chaotic map reported in the literature is the polynom type-c fractal map, which generates continuous real output with three dimensions and 18 seed parameters [36].

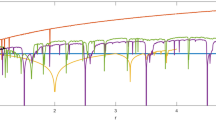
To examine the chaotic parameter, range bifurcation diagrams are plotted. These diagrams show the relationship between chaotic states and their corresponding control parameters. Lyapunov exponent is the parameter the plays a heavy role in deciding whether the chaotic map is useful in cryptography. This exponent shows high sensitivity to a slight change in the seed parameters, such as initial conditions and control parameters. The correlation coefficient allows us to determine whether the system has any correlation with the initial parameters or behaves totally chaotic. If the correlation coefficient is close to one, then the system is fully deterministic. If the correlation coefficient is close to 0, complete chaotic behavior is ensured. There are four different test suites that are generally used to evaluate the randomness of the pseudo-random number generator. They are National Institute of Standards and Technology (NIST) Special Publication (SP) 800-22, DIEHARD, ENT and TestU-01.

The mathematically simpler chaotic maps are popular e.g. Zig-zag reported by Nejati [37]. The equation of Zig-zag map is as shown in Eqs. 1 to 3 for values of $X_{n}$ Varying between $-$1 to 1.

$$\begin{aligned} x_{n+1}= & {} - m(x_{n} + 2/|m|) \end{aligned}$$

(1)

$$\begin{aligned} x_{n+1}= & {} m x_{n} \end{aligned}$$

(2)

$$\begin{aligned} x_{n+1}= & {} - m(x_{n} - 2/|m|) \end{aligned}$$

(3)

Also another simpler map is sawtooth. The equation of Sawtooth Map is as shown in Eq. 4

$$\begin{aligned} x_{n+1} = 2x_{n}(mod 1) \end{aligned}$$

(4)

Fig. 3

Two-dimensional X-Y plots of different chaotic maps. a It is observed that the Ikeda chaotic map [20] has opposite characteristics as compared to the Hitzl-Zele and Henon chaotic maps. The Ikeda chaotic map has a half semicircular pattern that is dominant on the left side of the X-Y plot. The map lies between 0.2 to 1.4 on the X-axis and $-$0.8 to 0.8 on the Y-axis. b The Hitzl-Zele chaotic map [21] is seen to be a half semicircular pattern that is dominant on the right side of the X-Y plot. The map lies between $-$1 to +1.5 on the X-axis and $-$0.2 to +0.3 on the Y-axis. c The Henon chaotic map [22] lies between $-$1.5 to +1.5 on the X-axis and $-$0.4 to +0.4 on the Y-axis. The map shows a half semicircular pattern that is dominant on the right side of the X-Y plot, which is similar to that of the Hitzl-Zele map. d The Tinkerbell chaotic map [23] shows the strongest chaotic behavior with an omnidirectional pattern. It lies between $-$1.2 to +0.4 on the X-axis and $-$1.5 to +0.5 on the Y-axis. All four maps lie between $-$2 to +3 on the X and Y axes

Fig. 4

a Generalized scheme for pseudo-random number generation using a chaotic map. Different chaotic maps are used to produce the chaotic series. These chaotic maps take the input in the form of control parameters and initial conditions and produce a chaotic function. A chaotic series adjustment is required sometimes where a chaotic map becomes periodic or deterministic. A converter to binary sequence is used to produce final pseudo-random 1-bit output based on decisions such as comparison or subtraction, minima, maxima, etc. b A sample bifurcation diagram of a logistic map showing different distances between consecutive bifurcations denoted by L1, L2, L3, etc. It can be observed that the ratio of these distances $\frac{L_i}{L_{i+1}}$ were found to be constant and represented by a term called Feigenbaum constant

Figure 3 shows the X-Y plots of different two-dimensional chaotic maps. Figure 3a shows the X-Y plot of the Ikeda chaotic map as obtained by Stoyanov et al. [20]. When compared to the Hitzl-Zele and Henon chaotic maps, the Ikeda chaotic map has the opposite properties. It can be seen that the Ikeda chaotic map has a half semicircular pattern that is dominant On the left side of the X-Y plot. The map has an X-axis range of $-$0.2 to 1.4 and a Y-axis range of $-$0.8 to 0.8. Figure 3b shows the Hitzl-Zele chaotic map obtained by Kordov et al. [21]. The equations for Hitzl-Zele chaotic map are as shown in Eqs. 5 to 7.

$$\begin{aligned} x(k + 1)= & {} 1 + y (n) - z(k) -x^{2}(k) \end{aligned}$$

(5)

$$\begin{aligned} y(k + 1)= & {} a.x(k) \end{aligned}$$

(6)

$$\begin{aligned} z(k + 1)= & {} b.x^{2}(k) + z(k) - 0.5 \end{aligned}$$

(7)

The Hitzl-Zele map is a half semicircular pattern that is dominant on the right side of the X-Y plot. The map has an X-axis range of $-$1 to +1.5 and a Y-axis range of $-$0.2 to +0.3. Figure 3c shows the Henon chaotic map which was obtained by Suryadi et al. [22]. This map has an X-axis range of $-$1.5 to +1.5 and a Y-axis range of $-$0.4 to +0.4. The map displays a half semicircular pattern that dominates the right side of the X-Y plot, similar to the Hitzl-Zele map. The plot shown in Fig. 3d is of the Tinkerbell chaotic map that was obtained by Stoyanov et al. [23]. The Tinkerbell chaotic map demonstrates the most chaotic behavior and makes an omnidirectional pattern on the X-Y plot. It ranges from $-$1.2 to +0.4 on the X-axis and from $-$1.5 to +0.5 on the Y-axis. The Ikeda, Henon, Hitzl-Zele, and Tinkerbell chaotic maps all have values ranging from $-$2 to +2.

2.1 Pseudo Random Number Generation Using Chaotic Maps

The first known pseudo-random number generator was proposed by John von Neumann [38] back in 1946. The method is known as the middle square method. It generates a poor-quality pseudo-random sequence but remains one of the important milestones in the evolution of pseudo-random generators.

Figure 4a shows a generalized scheme for generating pseudo-random numbers using a chaotic map. The chaotic series is generated using various types of chaotic maps. These chaotic maps take control parameters and initial conditions as input and produce a chaotic function. Sometimes, when a chaotic map becomes periodic or deterministic, a chaotic series adjustment is required. A binary sequence converter is used to generate the final pseudo-random 1-bit output based on decisions such as comparison, subtraction, minima, maxima, and so on. Figure 4b shows a sample logistic map bifurcation diagram showing different distances between consecutive bifurcations denoted by L1, L2, L3, and so on. It can be seen that the ratio of these distances was discovered to be constant and is represented by a term known as the Feigenbaum constant, which is given by $\frac{L_i}{L_{i+1}}$.

Cang et al. [39] designed a pseudo-random number generator based on the Sprott system. They have used Finite Precision Period Calculation (FPPC) to calculate the repetition rate. They also proved how a fix-point notation can avoid the degradation of chaotic maps because of precision. To show the validation of their pseudo-random generator, they have used the NIST statistical test suite. They tested their random numbers for the randomness of a scrambled sequence, correlation, key-space, entropy, histogram, linear complexity, and sensitivity of the key.

Lv et al. [40] have given different shortcomings of C-programming in pseudo-random number generation. They have also proposed a method to enhance the versatility of the random number.

Krishnamoorthi et al. [33] have used a turbulence-padded chaotic map to generate the pseudo-random numbers. Their method increased the periodicity and chaotic behavior. The proposed method was tested with the NIST SP 800-22 statistical test suite. They found that their proposed pseudo-random number generator increased 3.6 % of the key space and 5 % computing performance over existing chaotic Pseudo-Random Number Generators (PRNG). Figure 10a shows the operational model of the turbulent padded chaotic map. Here, a logistic map is used to create the root chaotic map of the turbulence padded chaotic map arrangement. The equation of Logistic Map is as shown in Eq. 8

$$\begin{aligned} x_{n+1} = rx_{n} (1-x_{n}) \end{aligned}$$

(8)

It is the first case in which lower-dimensional chaotic maps are more computationally efficient than higher-order chaotic maps.

As shown in Fig. 3b Kordov et al. [21] have used Hitzl-Zele chaotic map to produce a pseudo-random number that decides a particular pixel in which a secret message needs to be hidden. They used Least Significant Bit (LSB) steganography in this application. The maximum Peak Signal-to-Noise Ratio (PSNR) value obtained by using their method was 81.22, a mean square error of 0.0005, and an entropy of 7.9999 bits/byte.

Stoyanov et al. [20] have shown an implementation of a chaotic map-based pseudo-random number generator on an Arduino platform. They called this system CHAOSA. As shown in Figure 3a they have used the Ikeda map with $\mu$ = 0.701. The mathematical equation for the Ikeda map is given by Eq. 9.

$$\begin{aligned} z_{n+1} =A + B z_{n}e^{i\left( \left| z_{n} \right| ^{2}+ C\right) } \end{aligned}$$

(9)

They found out that their entropy was 7.999 bits/byte. They tested their system for a data length of 250 million bytes and found that the $\chi ^2$ value obtained by them was 288.88, which was 11 % better. Their correlation coefficient was 0.00006. They tested the randomness of the system on the DIEHARD and NIST SP 800-22 test suite.

Their team has also developed another pseudo-random number generator using two Tinkerbell maps [23].

The equation of Tinker-bell Map is as shown in Eq. 10

$$\begin{aligned} x_{n+1} = x_{n}^{2} - y_{n}^{2} + ax_{n} + by_{n} \end{aligned}$$

(10)

They have tested their number generator with NIST, DIEHARD, and ENT test suite. Figure 3d shows the Tinkerbell map implemented on C++. They found they could reach a speed of 0.49 Mbits/sec, which was larger than Yang et al. [41]. They produced a thousand sequences of 1 million bits and their entropy could reach up to 7.999 bits/byte and $\chi ^2$ could reach up to 240.50, which gets better by 73 % with time.

Moysis et al. [25] has developed a pseudo-random bit generator using multiple digit comparison. They have used multiple maps to produce the pseudo-random bit after comparing the results of each bit generated from all the maps. The majorly used maps were a logistic map, sine map, Renyi map, Chebyshev map, cubic map, logistic may map, coupled sine map, sine-sinh-sine map, and finally cubic logistic map.

The equation of Cubic map is as shown in Eq. 11

$$\begin{aligned} a x ^{3} + b x^{2} + c x + d = 0 \end{aligned}$$

(11)

The equation of Chebyshev Trignometric Map is as shown in Eq. 12

$$\begin{aligned} x_{n}(\theta )=COS(n X ARCCOS\theta ) \end{aligned}$$

(12)

The equation of Renyi map is x(n+1)=$\beta$x(mod1), where we assume that $\beta$ is greater than 1.

The bifurcation map is as shown in Fig. 6a. They also used the Lyapunov exponent of all the mentioned maps. They could reach the entropy of 7.9968 bits/byte. As an application of their pseudo-random sequence, they have shown QR code generation and image encryption.

Akhshani et al. [26] has developed a pseudo-random number generator based on the quantum chaotic map. The mathematical equation of the quantum chaotic map is given by Eqs. 13 to 15.

$$\begin{aligned}&\displaystyle x_{n+1} = r \left( x_{n} - \left| x_{n} \right| ^{2} \right) - ry_{n} \end{aligned}$$

(13)

$$\begin{aligned}&\displaystyle y_{n+1} = -y_{n}e^{-2\beta } + e^{-\beta } r\left[ \left( 2 - x_{n} - x^{*}_{n}\right) y_{n} - x_{n}z^{*}_{n} - x^{*}_{n}z_{n}\right] \end{aligned}$$

(14)

$$\begin{aligned}&\displaystyle z_{n+1} = -z_{n}e^{-2\beta } + e^{-\beta }r\left[ 2\left( 1-x^{*}_{n}z_{n} - 2x_{n}y_{n}-x_{n}\right) \right] \end{aligned}$$

(15)

They have used different values of the controlling parameter r to produce different bifurcation diagrams of the quantum map as shown in Fig. 7c–f. they have also shown a comparison of different non-periodic chaotic maps where they found Henon map with B = 0.3 and Rossler map with A and B = 0.1. The equation of Rossler Map are as shown in Eqs. 16, 17 and 18

$$\begin{aligned}&\displaystyle \frac{dx}{dt} = -y-z \end{aligned}$$

(16)

$$\begin{aligned}&\displaystyle \frac{dy}{dt} = x+ay \end{aligned}$$

(17)

$$\begin{aligned}&\displaystyle \frac{dz}{dt} = b+z(x-c) \end{aligned}$$

(18)

Where, the most commonly used values of a, b, and c are 0.1, 0.1, and 14 respectively.

Fig. 5

a A generalized scheme to obtain image encryption with the help of chaotic maps. An input image is fed to the channel splitter that converts a 3-dimensional image into 1-dimensional series of numbers. This is achieved by converting RGB channels as separate color channels and then splitting each row and appending them in a single sequence. A secret key is also provided to decide the type of chaotic map and initial conditions. Once the chaotic map is ready, the confusing sequence acts as per the chaotic map encrypting the image and consecutive confusion and diffusion cycles are repeated for N rounds to produce the final encrypted image. The number of rounds is also sometimes determined by the secret key. b Medical chest x-ray gray-scale image fed as an input to the image encrypter. c RGB input image of vegetables fed to the encrypter. d Histogram of the gray-scale medical input image [24]. e Color histogram of the RGB vegetables input image [24]. f Encrypted output image of the gray-scale medical image [24]. g Encrypted output image of the RGB vegetable image [24]. h Histogram of the gray-scale medical image showing that all pixels have been converted to the same value [24]. i Histogram of RGB vegetables image showing that all pixels have been converted to the same value [24]

Fig. 6

Bifurcation map for a Cubic logistic map [25], b Henon map [26], c Cosine map [27] and d Rossler map [26]. The control parameter of the chaotic map dictates the chaotic behavior. Here the control parameter is given by r and the control states are shown by X. As the value of the controlling parameter r increases the bifurcation diagrams show an expansion in the output values that they take (X) for the cubic logistic map and Rossler map, whereas, the Henon and Cosine maps remain flat

Fig. 7

a Analysis of lemniscate chaotic maps behaviour bifurcation diagram shown between r is 0 to 20 [28]. Complete chaotic behaviour is seen with fractal at around r = 1. b State-space trajectory of X(n) generated with by PRNG Chaotic Sequence (CS) [29]. Bifurcation diagram of different values of the control parameter r ranging from 3.85 - 3.99 of a quantum map [26]. At r = 3.85 c shows complete bifurcation till $\beta$ = 4 and then becomes non random. At r = 3.88 d shows a complete random behaviour with fractal around $\beta$ = 4. At r= 3.93 e a flat bifurcation diagram is seen and at r =3.99 (f) another fractal behaviour around $\beta$ = 5.5 is seen

Fig. 8

a Illustration diagram for encryption and decryption of a gray scale image (Lenna) as done by Hamza et al. [30]. The plain image is fed to Algo1. Here, the Algo 1 is based on 2D Zaslavsky chaotic map and corresponding encryption keys I1, I2, I3, I4, I5 are used to produce the encrypted image. I2 is produced from secret key and plain image and I3 to I5 transformation is looped 5 times. The entire decryption process is a reverse of an encryption process and C2, C3, C4, C5 are the decryption matrices. The transformation from C2 to C4 is looped 4 times. Hence, the proposed encryption mechanism with the Zaslavsky map is symmetric and reversible. b The plain image is passed through high-efficiency scrambling, image rotation, and random order substitution four times. The decision on random order is as per the secure key and LSC map. Finally, the cipher image is produced as per the LSC chaotic sequence [31]

Fig. 9

a Flow diagram of microcontroller software implementation by Cicek et al. [32]. The microcontroller is initialized with initial settings and chaotic map initial seeds. The chaotic map parameters are then found out, and the data is transferred via serial to USB port onto a computer. Based on the current, the next values are calculated as per the chaotic map. Further, the current values are updated, and the process continues. b Measurement setup for microcontroller-based random number generator. The measurement is done via a computer-based oscilloscope (analog discovery). c Barnsley Fern discrete chaotic map represented in X-Y dimension and implemented on Matlab. d Signal generated at the output of the random number generator with logic 0s and 1s. e Microcontroller output results for Barnsley Fern discrete chaotic map implemented on Arduino

Fig. 10

a Operational model of the turbulent padded chaotic map as shown by Krishnamoorthi et al. [33]. Here a logistic map is used to form the root chaotic map of the arrangement of turbulence padded chaotic map. It’s the first case showing how the lower dimensional chaotic maps can be proved computationally efficient than higher-order chaotic maps. b Double chaotic image encryption process used by Pan et al. [34]. Here the chaotic sequence generator 1 and chaotic sequence generator 2 are compared to produce a double chaotic random sequence generator. The output of the generator is fed to the encryption block where the clear image gets encrypted into a ciphered image, which is then used for information transfer. A similar double chaotic map is used for decryption, ensuring the system to be symmetric at both ends. The chaotic numbers from both the generators are XORed and one previous state is further XORed and finally, modulo N operation was carried to produce a confusing output. c True random number generator using Henon and logistic map as shown by Suryadi et al. [22]. The process employs a Sample and Hold (S and H) block, which receives the sampling clock. The output of the S and H block is fed to a 2D non-linear functional block, which was the first chaotic system implemented with the Henon map. The Henon map output is then fed into a 1D non-linear functional block that is a logistic map, and the final output is compared to a threshold. If the value exceeds the threshold, logic 1 is produced at the comparator’s output, otherwise logic 0 is produced. d Arnold Cat map used by Avarouglu et al. [35]. Here the map that looks similar to the face of a cat is transformed into a completely chaotic map using translation rotation and scaling operations along with modulo 1 operator

The bifurcation diagrams for the Henon map are as shown in Fig. 6b and for Rossler map is as shown in Fig. 6d. They achieved an entropy of 7.999995 with a $\chi ^2$ value of 255.19 and a correlation coefficient of 0.0001. To validate the results, they have shown NIST SP 800-22 test suite, DIEHARD test suite, ENT and TestU-01.

Alawida et al. [27] have shown different applications of digital cosine chaotic map. The bifurcation diagram of a cosine map is as shown in Fig. 6c. The equation of cosine map is as shown in Eq. 19.

$$\begin{aligned} x_{n+1} = G ( F(x_{n})) ) \end{aligned}$$

(19)

They could achieve a speed of 2.11 Mbits/sec. They generated pseudo-random numbers to extract 8-Bit integers directly from the chaotic system.

CICEK et al. [32] has developed a microcontroller-based random number generator using discrete chaotic map. They implemented Lozi, Tinkerbell, and Barnsley Fern’s discrete chaotic maps onto an Arduino microcontroller.

The equation of Lozi Map are as shown in Eqs. 20 and 21

$$\begin{aligned}&\displaystyle x_{n+1}=1-\alpha |x_n|+y_n \end{aligned}$$

(20)

$$\begin{aligned}&\displaystyle y_{n+1}=\beta x_n \end{aligned}$$

(21)

The equation of Barnsley-fern Map are as shown in Eq. 22

$$\begin{aligned} f(x,y)= [a b; c d][x y]+[e f] \end{aligned}$$

(22)

where, a, b, c, d, e, and f are coefficients of the equations.

Figure 9a generalized flow chart of microcontrollers software implementation. The first step was to load the initial settings and chaotic map initial seeds into the microcontroller. The chaotic map parameters are then determined, and the data is transferred to a computer via a serial to USB port. The chaotic map is used to calculate the next values based on the current value. The current values are then updated, and the process is repeated. Figure 9b is the measurement setup for a random number generator based on a microcontroller. Here, a computer-based oscilloscope is used to perform the measurement (analog discovery). The Barnsley Fern discrete chaotic map in X-Y dimension, implemented in MatLab is as shown in Fig. 9c. Figure 9d shows the output signal made up of logic 0s and 1s generated at the output of the random number generator. Results of microcontroller output for the Barnsley Fern discrete chaotic map implemented on Arduino are as shown in Fig. 9e.

Avarouglu et al. [35] has designed a pseudo-random number generator using Arnold Cat map. The representation of an Arnold Cat map is as shown in Eq. 23.

$$\begin{aligned} \Gamma : \left( x,y \right) \rightarrow \left( 2x+y, x+y \right) mod 1 \end{aligned}$$

(23)

They have shown the implementation of both Arnold Cat map 1 and Arnold Cat map 2. Their correlation coefficient was as low as 0.06. Figure 10d shows the Arnold Cat map. The map that resembles a cat’s face is transformed into a completely chaotic map using translation, rotation, and scaling operations, as well as the modulo 1 operator.

Yu et al. [42] developed a five-dimensional hyperchaotic four-wing memristive system for the generation of pseudo-random numbers. They have used Field Programmable Gate Array (FPGA) to implement their PRNG. The initial simulations of FPGA were done on VIVADO-2018.3 and then synthesized on ZYNQ-XC7Z020. They used 16 shift registers and 15 levels XOR chains in their post-processing. Their PRNG could reach a maximum operating frequency of 138.33 MHz with 15.367 Mb/sec. To test their results, they have also used NIST 800.22 statistical standards.

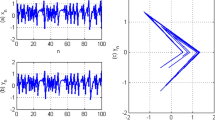
Dridi et al. [29] have recently published an FPGA-based design that implemented PRNG using a chaotic sequence they have used the Spartan-6 board. They have Side-channel AttacK User Reference Architecture - G (SAKURA-G) to implement the pseudo-random numbers on FPGA hardware using VHDL. Their produced state space trajectory for X(n) is as shown in Fig. 7b. They achieved a correlation coefficient of 0.0064.

Saber et al. [28] have used a low-power PNRG based on the Lemniscate Chaotic Map (LCM). The equation of Lemniscate Map is as shown in Eq. 24

$$\begin{aligned} \sqrt{(x-a)^2+y^2}\sqrt{(x+a)^2+y^2}=a^2. \end{aligned}$$

(24)

The bifurcation diagram is as shown in Fig. 7a. Fractal behaviour is seen up to r = 1. They have used a Spartan-6 FPGA board to implement their PRNG. They achieved an almost 48 % reduction in resource consumption and 34.6 % reduction in power.

2.2 True Random Number Generator Using Chaotic Map

Suryadi et al. [22] has developed a true random number generator based on Henon and logistic map. The Henon map is represented by Eq. 25 and the logistic map is represented by Eq. 26.

$$\begin{aligned}&\displaystyle x_{n+1} = 1- ax{_{n}}^{^{2}}+ y_{n} \nonumber \\&\displaystyle y_{n+1} = bx^{_{n}} \end{aligned}$$

(25)

$$\begin{aligned}&\displaystyle x_{n+1} = rx{_{n}}\left( 1- x_{n} \right) \end{aligned}$$

(26)

The Henon map used by them is shown in Fig. 3c plotted in X-Y dimension with 10000 iterations. They designed a totally random number generator and simulated using LabView. Their proposed design is as shown in Fig. 10c. That uses sample and hold block that receives the sampling clock and feeds that information to 2D non-linear functional block which is the first chaotic system implemented with Henon map. The output of the Henon map is fed to 1D non-linear functional block, which is a logistic map and the final output is compared with a threshold. If the value exceeds the threshold, logic 1 is produced at the output of the comparator and 0 otherwise. Their entropy was 0.9998.

Recently, Nannipieri et al. [43] developed a true random number generator based on Fibonacci-Galois Ring Oscillators. They implemented the proposed methodology on FPGA. They could achieve a throughput of 400Mbps and achieved entropy of 0.995 bytes per byte. They used 190 registers to implement the proposed true random number generator. Similar work was reported in 2019 by Demir et al. [44] but, they required 1115 gates and 4.811 mWatt of power consumption.

Wu and his team designed true random number generators based on semiconductor super-lattice chaos and further implemented it [45]. They could achieve a maximum bit rate of 300 Mbps for generating random bits. Wu and his team implemented the proposed mechanism using FPGA.

The traditional method of TRNG can it be oscillator-based or thermal noise based is limited to a few hundreds of bits per second wheres as the proposed methods like Wu takes advantage of high-speed semiconductor super-lattice chaos which is upcoming technology. Researchers may explore the way to generate RNGs at a faster rate, which is the current research gap.

2.3 Multimedia Encryption

2.3.1 Image Encryption Using Chaotic Maps

Figure 5a shows a generalized scheme for obtaining image encryption using chaotic maps. A 3-dimensional image is fed into the channel splitter, which converts it into a 1-dimensional series of numbers. This is accomplished by converting RGB channels to separate color channels, then splitting and appending each row in a single sequence. In addition, a secret key is provided to determine the type of chaotic map and initial conditions. Once the chaotic map is complete, the confusing sequence encrypts the image in accordance with the chaotic map, and successive confusion and diffusion cycles are repeated for N rounds to produce the final encrypted image. In certain cases, the secret key can also influence the number of rounds. Koppu et al. [24] has developed a fast chaotic cryptography-based image encryption system. They have used a Hybrid Chaotic Magic Transform (HCMT) to produce the encrypted image from the secret key. They achieved a correlation of 0.0012 using their HCMT, which is a combination of Lanczos algorithm with Chaotic Magic Transform (CMT). Their result outperformed the existing CMT method used by Hua et al. [46] having a correlation coefficient of 0.042 and 3D chaotic method used by Chen et al. [47] having a correlation coefficient of 0.014. The images depicted in Fig. 5b and c, show the images of a gray-scale medical chest x-ray and RGB vegetables. These images were used by Koppu et al. [24] and were given as input to an image encryption system. Figure 5d shows the histogram obtained from the input gray-scale medical image depicting the different pixel values. Figure 5e shows the color histogram obtained from the input RGB vegetable image depicting the different R,G,B pixel values. From Fig. 5f we can observe the encrypted output image of the gray-scale medical image and Fig. 5g is the encrypted output image of the RGB image obtained from the chaotic system. Figure 5h and (i) depict the histograms obtained from the output encrypted images, demonstrating that all the pixels of the input images have been converted to the same value, thus encrypting it entirely.

Gupta et al. [48] have designed an image encryption scheme using a reconfigurable pseudo-random number generator. Their PRNG was dependent on the 4D hyperchaotic system. They implemented the PRNG on Zynq (XC7Z045) FPGA board sing Vertix5 and Verilog-HDL. For analysis, they used the Matlab tool and NIST test suite. Their hardware can operate at 79.1 MHz with a data rate of 1898.4 Mb/sec. The memory utilization of the Zynq board was up to 1.77 % max using S-box encryption.

Hua et al. [31] have designed a cosine-transform-based chaotic system for image encryption. They have used an encryption scheme based on high-efficiency scrambling. They could achieve a correlation coefficient of 0.000181. Figure 8b shows the Logistic Sine Cosine-Image Encryption Scheme (LCS-IES) that they have used. The plain image is processed four times using high-efficiency scrambling, image rotation, and random order substitution. The random order is determined by the secure key and the LSC map. Finally, the LSC chaotic sequence is used to generate the cipher image.

Tang et al. [49] used double spiral scans and chaotic maps for encrypting the image. They have divided the image into an overlapping box of pixels and then used a double spiral scan to scramble it. The start point of a double spiral scan was selected using Henon chaotic map. They could execute the entire encryption in 2.79 seconds.

Deng et al. [50] used chaotic mapping for digital image encryption using a scrambling algorithm called XZQ. They have used chaos-Add Image Feature (AIF) to perform encryption. They could achieve encryption in 1.2157 seconds.

Hamza et al. [30] have designed an image encryption algorithm based on Zaslavsky chaotic map. The Zaslavsky chaotic map is represented by Eqs. 27 and 28.

$$\begin{aligned}&\displaystyle x_{n+1} = \left[ x{_{n}+ v\left( 1 + \mu y_{n} \right) } + \epsilon v \mu \cos \left( 2\varPi x^{_{}}{_{n}} \right) \right] (mod 1) \end{aligned}$$

(27)

$$\begin{aligned}&\displaystyle y_{n+1} = e^{-\gamma }(y_{n} + \epsilon cos\left( 2\varPi x^{_{}}{_{n}} \right) ) \end{aligned}$$

(28)

Their entropy could reach up to 7.9998 and correlation coefficient of 0.0002. To verify the quality of the encryption, they performed the Number of Changing Pixel Rate (NPCR) test and the Unified Averaged Changed Intensity (UACI) test. The encryption time of their method was about 0.23 seconds. Figure 8a shows the diagram for the encryption and decryption of a gray scale Lenna image. The plain Lenna image is fed to the Algo 1, which is based on a 2D Zaslavsky chaotic map. The encrypted image is produced using the corresponding encryption keys I1, I2, I3, I4, and I5. I2 is created by combining a secret key and the plain image, and the I3 to I5 transformation is repeated five times. The entire decryption process is the inverse of the encryption process, and the decryption matrices are C2, C3, C4, C5. The transformation from C2 to C4 is repeated four times. As a result, the proposed encryption mechanism based on the Zaslavsky map is symmetric and reversible.

Pan et al. [34] designed a double logistic chaotic map for the production of encrypted image. They have used both color and gray scale images and shown that the histograms are flat for the encrypted image. Their correlation coefficient was 0.0013 and entropy was in the range of 7.98. Figure 10b shows the image encryption process using a double chaotic map. Here, the chaotic sequence generators 1 and 2 are compared to create a double chaotic random sequence generator. The generator’s output is fed into the encryption block, where the clear image is encrypted into a ciphered image, which is then used for data transfer. For decryption, a similar double chaotic map is used, ensuring that the system is symmetric at both ends. The chaotic numbers from both generators are XORed, and one previous state is further XORed followed by a modulo N operation to produce a confusing output.

Recently, Kari et al. [51] have developed a hybrid chaotic map to encrypt gray scale image files. They have Arnold’s cat maps perform confusion and diffusion done by combining sine, logistic, and tent. These operations were then XORed to provide extra security. Their proposed method achieved an entropy as high as 7.999978 and a correlation coefficient as low as 0.0031, with the lowest execution time being 351 ms. Although they had good security, the combination of multiple maps results in a higher execution time.

2.3.2 Audio Encryption Using Chaotic Maps

Adhikari et al. [52] have developed an audio encryption method based on Henon-Tent chaotic pseudo-random number generator. They used 1D 16 bit uncompressed audio file as the input. The output of the chaotic Henon map and Tent map was XORed to generate a secret key. The equation of Tent Map is as shown in Eq. 29

$$\begin{aligned} f_{\mu } = \mu _{min}(x,1-x) \end{aligned}$$

(29)

This secret was then XORed with the original input file to generate the ciphered audio file.

Alemami et al. [53] have used the logistic chaotic map and sine chaotic map to encrypt speech signals. Initially, they processed the input speech signal using Fast Fourier Transform (FFT). A logistic function was then developed to create confusion and a diffusion key was developed using the sine map. The equation of sine map is as shown in Eq. 30.

$$\begin{aligned} x_{n+1} = A.\sin (\varPi . (x_{n})) \end{aligned}$$

(30)

Lastly, the XOR operation was done on the outputs of the logistic map and sine map to get the encrypted output. They tested the quality of encryption by finding out the correlation coefficient, which was as low as 0.0047094.

Shah et al. [54] have developed a novel three-dimensional chaotic map and have tested its use by applying it to encrypt audio. They have used the map to shuffle around the data points of the input audio file to encrypt the original file. The input audio of 15-bits is split into two sequences which are either 7-bit or 8-bit long. These sequences are further substituted with 7 x 7 S-boxes generated by applying Mobius transformation and then the chaos system is applied to it to scramble the media. XOR operation is applied to the scrambled 7-bit and 8-bit to create the final encrypted file. The correlation coefficient using their proposed method was as low as 0.0010 and the entropy was as high as 15.9981. The execution time varied for files of different lengths ranging from 6.341 seconds for a file of size 32,000 kb to 0.015 seconds for a file of size 32 Kb. They achieved a Signal Noise Ratio as low as 8.4426 and a Mean Squared Error as high as 3.5231$\times$10$^4$. Although their system shows good security, it takes up a lot of time when applied to large audio files. In an earlier study by Shah and his team [55] they have applied the same technique of substituting the audio files with 8 X 8 S-boxes but, here they had applied the Henon chaotic map to create confusion. A permutation network that uses the Henon chaotic map was developed to shuffle the files in a piecewise manner. Their correlation coefficient was as low as 0.0014 and entropy was as high as 7.9995.

Table 1 Different data rates at which the random bits are generated or the encryption was carried at

Fig. 11

Comparison of different hardware resources utilized while implementing different chaotic maps on FPGA. a The number of registers and FPGA resources utilized in different methods. b Operating frequency in MHz for different FPGA boards used for implementing chaotic maps. c Execution time in seconds for different methods that implemented the pseudo-random number generators using chaotic maps. d Parametric analysis of chaotic maps used for image encryption applications. The ideal change in pixel rate should be around 100 % and most of the methods in literature have already achieved 99 %. The overall average change in intensity was about 33

Table 2 Comparison of different methods of generating pseudo-random numbers using chaotic maps in terms of their correlation coefficient and entropy. The correlation coefficient was found out to be less than 0.09 and the entropy was always found to be in the range of 7.9 and above

3 Discussions

Table 1 shows encryption can be achieved in Mbits/second. The highest data-rate was achieved by Alawida et al. [27] with 2.12 Mbits/second. On the other hand, the lowest rate was by Liu et al. that could reach only up to 41.5 bits/second. Though this data rate is completely dependent on the machine on which the computations are done, typically 11th generation i9 processors with 32 GB RAM should be able to produce at least a few Mbits/second. It can be seen from the table that the recent papers have exponential growth in the number of data bits handled per second b the machine. Whereas the earlier decade computations could handle only Kbits/second speed.

Table 2 shows the comparison of multiple methods reported in the literature that use chaotic maps for the generation of pseudo-random numbers and/or using them for encryption. The comparison was done on the basis of the correlation coefficient and entropy. For a random number generator, the correlation coefficient between its subsections ideally should be zero but for all practical reasons, it should be as low as possible. There was a wide range of correlation coefficients reported in literature highest being 0.0857 by Tang et al. [49] and the lowest being 0.00006 by Stoyanov et al. [20]. Though there is a difference of three orders of magnitude between the highest reported correlation coefficient and the lowest one. It is impressive that none of the methods has even crossed 0.1 as a correlation coefficient (not even a 10 % matching). This proves that chaotic maps are highly random. Thus making any chaotic map-based pseudo-random number generator highly random in nature and extremely difficult to break through the security provided by them. The ideal value of entropy should be 8 bits per byte. Most of the works in literature have reported an entropy value very close to this ideal value. The highest value of entropy was reported was 7.999995 by Akhshani et al. [26] and the lowest was reported was 7.98 by Pan et al. [34]. This proves that chaotic maps result in systems that can generate an output with a lot of information packed into one byte. This makes chaotic map-based systems extremely difficult to predict, hence making them suitable to be used for applications like OTP generation and encryption. The Ikeda map (shown in Fig. 3a) used by Stoyanov et al. [20] to develop a pseudo-random number generator has proven to be able to have a decent entropy with a very low value of correlation coefficient simultaneously.

Figure 11 shows the comparison of various hardware resources used while implementing various chaotic-map-based applications on an FPGA. Figure 11a depicts the total number of registers and FPGA resources used in various methods. The operating frequency in MHz for various FPGA boards and the multipliers used in them for chaotic map implementation are shown in Fig. 11b. Figure 11c shows the execution time in seconds for various methods that used chaotic maps to implement pseudo-random number generators. Karakaya et al. [70] have achieved the highest operating frequency of 59.492 MHz with 165 registers, 311 FPGA resources, and 22 multipliers, which was the lowest number of hardware resources used in the reported literature. Hamza et al. [30] achieved the lowest execution time of 0.23 seconds while using a 2D Zaslavsky chaotic map for image encryption. Figure 11d depicts the parametric analysis of chaotic maps, which are used in image encryption applications. The ideal change in pixel rate should be around 100 %, and most methods in the literature have already succeeded in achieving around 99 %. Saber et al. [28] achieved the highest change in pixel rate of 99.661 % and highest average intensity change of 33.448 using the Lemniscate chaotic map for image encryption.

4 Applications of Chaotic Maps In Data Science

Chaotic maps are dynamic systems that are applied to different applications to further create confusion in the original data or to encrypt it. But chaotic maps on their own also generate very large amounts of random data due to their chaotic behaviors. The large periodicity of these maps leads to the generation of millions and millions of bits before the pattern could repeat. When a chaotic equation is plotted, it is evident that it creates a lot of data along its random trajectory that makes it impossible for a hacker to perform pattern analysis attacks.

Another very important application of chaotic maps in the data science field is their ability to encrypt data. In today’s tech-savvy world, a vast majority of the data is generated online, which has increased the need for this data to be encrypted to provide security and prevent hacking. PRNGs developed using chaotic maps can also be applied for the protection of big data. Because of the social networking sites, millions of multimedia files are being generated every second, making chaotic map-based PRNG a crucial tool for encrypting this data which is floating online. This makes the study of chaotic maps and PRNG very important in the field of data science.

5 Summary

There are multiple ways of implementing pseudo-random number generators. Chaotic map for this specific application seems the perfect choice as it has chaos in it by default. This paper briefly covers many ways of generating pseudo-random numbers using different chaotic maps. Many of the reported literature work was not only limited to a software implementation but further was implemented on traditional hardware like FPGA or modern controllers like Arduino, Raspberry Pi. Few of the manuscripts covered in this summary use the chaotic behavior of these mathematical chaotic maps to encrypt the multimedia sources such as audio and image. Image encryption is a very popular application of chaotic maps and people have gone on to implement it using FPGA hardware as well. We found very few papers working on audio encryption or even, for that matter, true random number generators using chaotic maps. There are other linear and non-linear dynamic systems, but we did not cover all of them as they were out of the scope of this manuscript. We tried to present a detailed review of how to use a chaotic map for a pseudo-random number generator and a comparison of different types of chaotic maps already being used.

There were different chaotic maps used to generate pseudo-random numbers. The most commonly used chaotic map is the logistic type in which cubic, 2D, May logistic, and B-exponential are some subtypes of logistic maps. Most of the maps were ranging between $-$1 to +1 in all three dimensions and forms an arbitrary shape per iteration. The Tinkerbell chaotic map is considered to be the most widespread in the X-Y dimension. Whereas the Ikeda map has smooth curvatures and therefore can be implemented on computationally low power systems such as Arduino. There were many trigonometry-based maps, mainly sine and cosine. The biggest advantage of a cosine map is its dependency on the initial value of the control parameter (r). Most of the chaotic maps have subtypes in the real space and complex space domain, e.g. exponential map belongs to the complex space domain and Tinkerbell map belongs to the real domain. There are newly introduced hyperchaotic maps such as hyper-attractor, hyper-Rossler, and hyper-Lorenz, which are the extension of their 3D equivalent in 4-dimension.

Typically reported literature shows the X-Y map that shows a pattern of the chaotic map. The overlapping lines seen in these patterns are generally not from the previous curve but a different curve and hence, even with slight overlapping, these chaotic maps are truly non-predictable. Also, there are chances that lines looking completely overlapped in 2D are far apart when seen in the 3D equivalent. It can be seen from the literature that the range from which the chaotic map varies can be from -2 to +2 and hence truncating it at 1 by modulo operation helps determine the output bit of the sequence. Typically, if the map value lies above 0.5, then logic bit ‘1’ is created and if map value is below 0.5 logic bit ‘0’ is created. The best way to see the fractal pattern of a chaotic map a bifurcation diagram is drawn. Where the ratio between consecutive lengths for the point of bifurcation is the same for the fractals. In the case of an image encryption application, many times, a key is used to set up the initial conditions. These key-based initial conditional encryptors are sensitive to the knowledge of key. Hence, a time-based seed along with the key is a better choice for initial condition selectors. W found that there were very few algorithms that allowed the user to select the chaotic map for their encryption. For the ease of the decryption process, typically a symmetric encryption scheme is chosen so that the algorithm that encrypts the image can be able to decrypt it. Because of the availability of the key and the correct algorithm, the person having encrypted output can easily decrypt the original image again. During the survey, it was observed that most of the images were RGB-based, and very few had done encryption of gray scale images. The histogram of the encrypted image should be a flat line around 0.5, if normalized. Whereas the histogram of the non-encrypted image looks like it has valleys and peaks.

There were different bifurcation maps, but mainly seen as a map that explodes or a map that remains flat. The exploding maps typically take larger fluctuating jumps at higher values of r. Whereas flat-type bifurcation diagrams can be used at very low values of r as well. Ideally, r should be chosen greater than 1.5 and within the range of 40, but this choice can be further user-defined as per the application. The hardware-based implementation of random-number generators totally depends on the number of bits the Arithmetic Logic Unit (ALU) of the microcontroller can handle. The speed of the random-number generator is controlled by the clock frequency of the controller. We found that at least 100 registers are used when the chaotic maps are implemented on the FPGA. The maximum operating frequency of an FPGA could reach 100 MHz and there is a well-defined research gap to reach at least a few GigaHertz frequencies of random number generation. Due to the complex mathematical calculation that a typical chaotic map has, the execution time of the entire sequence could not cross 0.2 seconds and we need pseudo-random number generators that can produce its entire file in a few milliseconds. Hence, chaotic map-based pseudo-random number generators are not suited for real-time applications but still can be used in applications like OTP generation and image encryption. Throughout the survey, we found that all the researchers achieved a correlation coefficient that was very close to the ideal value of zero and the entropy reported by maximum researchers crossed 7.99, whose ideal value is 8 bits per byte. We hope that people will keep on implementing the chaotic maps for different schemes in random generation and may find extremely secure systems built on it. This will help in the complete prohibition of electronic fraud.

Security is not the only aspect of chaotic map-based pseudo-random number generation but it can also be used in multi-media encryption, video-game animations, digital advertisements, simulation of chaotic systems, chaotic missile systems, etc.