Abstract
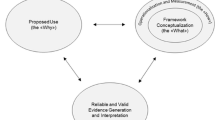
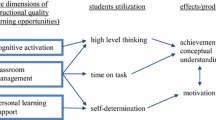
Researchers from different fields have developed different observational instruments to capture instructional quality with a focus on generic versus content-specific dimensions or a combination of both. As this work is fast accumulating, the need to explore synergies and complementarities among existing work on instruction and its quality becomes imperative, given the complexity of instruction and the increasing realization that different frameworks illuminate certain instructional aspects but leave others less visible. This special issue makes a step toward exploring such synergies and complementarities, drawing on the analysis of the same 3 elementary-school lessons by 11 groups using 12 different frameworks. The purpose of the current paper is to provide an up-to-date overview of prior attempts made to work at the intersection of different observational frameworks. The paper also serves as the reference point for the other papers included in the special issue, by defining the goals and research questions driving the explorations presented in each paper, outlining the criteria for selecting the frameworks included in the special issue, describing the sampling approaches for the selected lessons, presenting the content of these lessons, and providing an overview of the structure of each paper.

Similar content being viewed by others
Notes
Lindorff and Sammons (this issue) have not developed the frameworks utilized in their work but combine existing frameworks to better understand instructional quality. Similarly, Berlin and Cohen (this issue) are not amongst the original developers of the CLASS instrument.
We would like to thank Heather C. Hill from the Harvard Graduate School of Education for generously giving access to these videotaped lessons to all researchers contributing to the special issue.
References
Ball, D. L. (1992). Magical hopes: Manipulatives and the reform of math education. American Educator, 16(2), 14–18, 46–47.
Ball, D. L., Lewis, J., & Thames, M. H. (2008). Making mathematics work in school. In A. J. Schoenfeld & N. Pateman (Eds.), A study of teaching: Multiple lenses, multiple views: Journal for research in mathematics education, monograph #14 (pp. 13–44). Reston: NCTM.
Bell, C. A., Gitomer, D. H., McCaffrey, D. F., Hamre, B. K., Pianta, R. C., & Qi, Y. (2012). An argument approach to observation protocol validity. Educational Assessment, 17(2–3), 62–87. https://doi.org/10.1080/10627197.2012.71501.
Blazar, D., Braslow, D., Charalambous, C. Y., & Hill, H. C. (2017). Attending to general and mathematics-specific dimensions of teaching: Exploring factors across two observation instruments. Educational Assessment, 22(2), 71–94. https://doi.org/10.1080/10627197.2017.1309274.
Blazar, D., & Kraft, M. A. (2017). Teacher and teaching effects on students’ attitudes and behaviors. Educational Evaluation and Policy Analysis, 39(1), 146–170. https://doi.org/10.3102/0162373716670260.
Blazar, D., Litke, E., & Barmore, J. (2016). What does it mean to be ranked a “high” or “low” value-added teacher? Observing differences in instructional quality across districts. American Educational Research Journal, 53(2), 324–359. https://doi.org/10.3102/0002831216630407.
Booker, L. N. (2014). Examining the development of beginning middle school math teachers’ practices and their relationship with the teachers’ effectiveness. Unpublished doctoral dissertation, Vanderbilt University, Nashville, Tennessee, USA.
Boston, M., Bostic, J., Lesseig, K., & Sherman, M. (2015). A comparison of mathematics classroom observation protocols. Mathematics Teacher Educator, 3(2), 154–175. https://doi.org/10.5951/mathteaceduc.3.2.0154.
Cantrell, S., & Kane, T. J. (2013). Ensuring fair and reliable measures of effective teaching. Seattle: Bill & Melinda Gates Foundation. http://www.metproject.org/reports.php. Accessed 19 Feb 2015.
Charalambous, C. Y., & Kyriakides, E. (2017). Working at the nexus of generic and content-specific teaching practices: An exploratory study based on TIMSS secondary analyses. The Elementary School Journal, 117(3), 423–454. https://doi.org/10.1086/690221.
Cohen, D. K. (2011). Teaching and its predicaments. Cambridge: Harvard University Press.
Common Core State Standards Initiative [CCSSI] (2014). Mathematics Standards. http://www.corestandards.org/Math/. Accessed 20 Feb 2014.
Creemers, B. P. M., & Kyriakides, L. (2008). The dynamics of educational effectiveness: A contribution to policy, practice, and theory in contemporary schools. London & New York: Routledge.
Cuoco, A. A., & Curcio, F. R. (Eds.). (2001). The roles of representation in school mathematics (NCTM 2001 Yearbook). Reston: NCTM.
Danielson, C. (2013). Enhancing professional practice: A framework for teaching (2nd edn.). Alexandria: Association for Supervision and Curriculum Development.
Dignath-van Ewijk, C., Dickhäuser, O., & Büttner, G. (2013). Assessing how teachers enhance self-regulated learning–A multi-perspective approach. Journal of Cognitive Education and Psychology, Special Issue of Self-Regulated Learning, 12(3), 338–358. https://doi.org/10.1891/1945-8959.12.3.338.
Doabler, C. T., Baker, S. K., Kosty, D. B., Clarke, B., Miller, S. J., & Fien, H. (2015). Examining the association between explicit mathematics instruction and student mathematics achievement. Elementary School Journal, 115(3), 303–333. https://doi.org/10.1086/679969.
Doyle, W. (1986). Classroom organization and management. In M. C. Wittrock (Ed.), Handbook of research on teaching (3rd edn., pp. 392–431). London: Macmillan.
Dubinski, W. N., Waxman, H. C., Brown, D. B., & Kelly, L. J. (2016). Informing teacher education through the use of multiple classroom observation instruments. Teacher Education Quarterly, 43(1), 91–106.
Gibbons, C. J. (2016). Variations of mathematics in college algebra instruction: An investigation through the lenses of three observation protocols. Unpublished Master’s thesis, Oregon State University, Corvallis, Oregon, USA.
Grossman, P., & McDonald, M. (2008). Back to the future: Directions for research in teaching and teacher education. American Educational Research Journal, 45(1), 184–205. https://doi.org/10.3102/0002831207312906.
Henry, M. A., Murray, K. S., & Phillips, K. A. (2007). Meeting the challenge of STEM classroom observation in evaluating teacher development projects: A comparison of two widely used instruments. http://sirc.mspnet.org/index.cfm/19945. Accessed 12 Feb 2013.
Hiebert, J., Gallimore, R., Garnier, H., Givvin, K. B., Hollingsworth, H., Jacobs, J., … & Stigler, J. (2003). Teaching mathematics in seven countries: Results from the TIMSS 1999 video study. U.S. Department of Education. Washington DC: National Center for Education Statistics.
Hill, H. C., Blunk, M., Charalambous, C. Y., Lewis, J., Phelps, G. C., Sleep, L., & Ball, D. L. (2008). Mathematical knowledge for teaching and the mathematical quality of instruction: An exploratory study. Cognition and Instruction, 26(4), 430–511. https://doi.org/10.1080/07370000802177235.
Hill, H. C., Charalambous, C. Y., & Kraft, M. (2012). When rater reliability is not enough: Teacher observation systems and a case for the G-study. Educational Researcher, 41(2), 56–64. https://doi.org/10.3102/0013189X12437203.
Horizon Research, I. (2000). Inside the classroom observation and analytic protocol. Chapel Hill: Horizon Research, Inc. http://www.horizon-research.com/instruments/clas/cop.pdf. Accessed 18 Sep 2008.
Horn, I. S. (2008). Accountable argumentation as a participation structure to support learning through disagreement. In A. J. Schoenfeld & N. Pateman (Eds.), A study of teaching: Multiple lenses, multiple views: Journal for Research in Mathematics Education, Monograph #14 (pp. 97–126). Reston: NCTM.
Kane, T. J., & Staiger, D. O. (2012). Gathering feedback for teaching: Combining high-quality observations with student surveys and achievement gains. Seattle: Bill & Melinda Gates Foundation. http://www.metproject.org/reports.php. Accessed 30 Nov 2012.
Kane, T. J., Taylor, E. S., Tyler, J. H., & Wooten, A. L. (2011). Identifying effective classroom practices using student achievement data. Journal of Human Resources, 46(3), 587–613. https://doi.org/10.3386/w15803.
Kilday, C. R., & Kinzie, M. B. (2009). An analysis of instruments that measure the quality of mathematics teaching in early childhood. Early Childhood Education Journal, 36(4), 365–372. https://doi.org/10.1007/s10643-008-0286-8.
Klieme, E., Pauli, C., & Reusser, K. (2009). The Pythagoras study: Investigating effects of teaching and learning in Swiss and German mathematics classrooms. In T. Janik & T. Seidel (Eds.), The power of video studies in investigating teaching and learning in the classroom (pp. 137–160). Münster: Waxmann.
Lampert, M. (2001). Teaching problems and the problems of teaching. New Haven and London: Yale University Press.
Learning Mathematics for Teaching Project. (2011). Measuring the mathematical quality of instruction. Journal of Mathematics Teacher Education, 14(1), 25–47. https://doi.org/10.1007/s10857-010-9140-1.
Leinhardt, G. (1993). On teaching. In R. Glaser (Ed.), Advances in instructional psychology (pp. 1–54). Hillsdale: Lawrence Erlbaum Associates.
Litke, E. G. (2015). The state of the gate: A description of instructional practice in algebra in five urban districts. Unpublished doctoral dissertation, Harvard University, Cambridge, MA.
Lockwood, J. R., Savitsky, T. D., & McCaffrey, D. F. (2015). Inferring constructs of effective teaching from classroom observations: An application of Bayesian exploratory factor analysis without restrictions. The Annals of Applied Statistics, 9(3), 1484–1509. https://doi.org/10.1214/15-AOAS833.
Marder, M., & Walkington, C. (2014). Classroom observation and value-added models give complementary information about quality of mathematics teaching. In T. Kane, K. Kerr & R. Pianta (Eds.), Designing teacher evaluation systems: New guidance from the measuring effective teaching project (pp. 234–277). New York: Wiley.
Martin-Raugh, M., Tannenbaum, R. J., Tocci, C. M., & Resse, C. (2016). Behaviorally anchored rating scales: an application for evaluating teaching practice. Teaching and Teacher Education, 59, 414–419. https://doi.org/10.1016/j.tate.2016.07.026.
Matsumura, L. C., Garnier, H., Slater, S. C., & Boston, M. (2008). Toward measuring instructional interactions ‘at-scale.’. Educational Assessment, 13(4), 267–300. https://doi.org/10.1080/10627190802602541.
McGuire, P. R., Kinzie, M., Thunder, K., & Berry, R. (2016). Methods of analysis and overall mathematics teaching quality in at-risk prekindergarten classrooms. Early Education and Development, 27(1), 89–109. https://doi.org/10.1080/10409289.2015.968241.
Mihaly, K., McCaffrey, D., Staiger, D., & Lockwood, J. R. (2013). A composite estimator of effective teaching (MET Project). The RAND Corporation. http://www.rand.org/pubs/external_publications/EP50155.html. Accessed 21 March 2015.
Mitchell, R., Charalambous, C. Y., & Hill, C. H. (2014). Examining the task and knowledge demands needed to teach with representations. Journal of Mathematics Teacher Education, 17(1), 37–60. https://doi.org/10.1007/s10857-013-9253-4.
Muijs, D., Kyriakides, L., van der Werf, G., Creemers, B., Timperley, H., & Earl, L. (2014). State of the art–teacher effectiveness and professional learning. School Effectiveness and School Improvement, 25(2), 231–256. https://doi.org/10.1080/09243453.2014.885451.
National Council of Teachers of Mathematics [NCTM] (2000). Principles and standards for school mathematics. Reston: NCTM.
Nowińska, E., & Praetorius, A. K. (2017). Evaluation of a rating system for the assessment of metacognitive-discursive instructional quality. In Proceedings of the tenth congress of the European Society for Research in Mathematics Education. https://keynote.conference-services.net/resources/444/5118/pdf/CERME10_0379.pdf. Accessed 30 Sept 2017.
Pianta, R., & Hamre, B. K. (2009). Conceptualization, measurement, and improvement of classroom processes: Standardized observation can leverage capacity. Educational Researcher, 38(2), 109–119. https://doi.org/10.3102/0013189X09332374.
Pinter, H. H. (2013). Patterns of teacher’s instructional moves: What makes mathematical instructional practices unique? Unpublished Doctoral Dissertation. University of Virginia, Charlottesville, USA.
Posner, T. (2008). Equity in a mathematics classroom: An exploration. In A. J. Schoenfeld & N. Pateman (Eds.), A study of teaching: Multiple lenses, multiple views: Journal for research in mathematics education, MONOGRAPH #14 (pp. 127–172). Reston: NCTM.
Praetorius, A. K., Pauli, C., Reusser, K., Rakoczy, K., & Klieme, E. (2014). One lesson is all you need? Stability of instructional quality across lessons. Learning and Instruction, 31, 2–12. https://doi.org/10.1016/j.learninstruc.2013.12.002.
Sammons, P., Lindorff, A. M., Ortega, L., & Kington, A. (2016). Inspiring teaching: Learning from exemplary practitioners. Journal of Professional Capital and Community, 1(2), 124–144. https://doi.org/10.1108/JPCC-09-2015-0005.
Sawada, D., Piburn, M. D., Judson, E., Turley, J., Falconer, K., Benford, R., & Bloom, I. (2002). Measuring reform practices in science and mathematics classrooms: The reformed teaching observation protocol. School Science and Mathematics, 102(6), 245–253. https://doi.org/10.1111/j.1949-8594.2002.tb17883.
Schaffer, E., Muijs, D., Reynolds, D., & Kitson, K. (1998). The mathematics enhancement classroom observation recording system, MECORS). Newcastle: University of Newcastle, School of Education.
Schlesinger, L., & Jentsch, A. (2016). Theoretical and methodological challenges in measuring instructional quality in mathematics education using classroom observations. ZDM Mathematics Education, 48(1–2), 29–40. https://doi.org/10.1007/s11858-016-0765-0.
Schlesinger, L., Jentsch, A., Kaiser, G., König, J., & Blömeke, S. (2018). Subject-specific characteristics of instructional quality in mathematics education. ZDM Mathematics Education, 50(3). (this issue).
Schoenfeld, A. H. (2008). On modeling teachers’ in-the-moment decision making. In A. J. Schoenfeld & N. Pateman (Eds.), A study of teaching: Multiple lenses, multiple views: Journal for research in mathematics education, monograph #14 (pp. 45–96). Reston, VA: NCTM.
Schoenfeld, A. H. (2013). Classroom observations in theory and practice. ZDM—The International Journal on Mathematics Education, 45(4), 607–621. https://doi.org/10.1007/s11858-012-0483-1.
Schoenfeld, A. J., & Pateman, N. (2008). (Eds.). A study of teaching: Multiple lenses, multiple views: Journal for research in mathematics education. Monograph #14. Reston: NCTM.
Smith, M. S., & Stein, M. K. (2011). 5 practices for orchestrating productive mathematics discussions. Reston: NCTM.
Strong, M. (2011). The highly qualified teacher: What is teacher quality and how do we measure it? New York: Teachers College Press.
Teddlie, C., Creemers, B. M. P., Kyriakides, L., Muijs, D., & Fen, Y. (2006). The international system for teacher observation and feedback: Evolution of an international study of teacher effectiveness constructs. Educational Research and Evaluation, 12(6), 561–582. https://doi.org/10.1080/13803610600874067.
Thompson, C. J., & Davis, S. B. (2014). Classroom observation data and instruction in primary mathematics education: Improving design and rigour. Mathematics Education Research Journal, 26(2), 301–323. https://doi.org/10.1007/s13394-013-0099-y.
Tsamir, P., Tirosh, D., Tabach, M., & Levenson, E. (2010). Multiple solution methods and multiple outcomes—is it a task for kindergarten children? Educational Studies in Mathematics, 73(3), 217–231. https://doi.org/10.1007/s10649-009-9215-z.
Van de Grift, W. (2007). Quality of teaching in four European countries: A review of the literature and application of an assessment instrument. Educational Research, 49(2), 127–152. https://doi.org/10.1080/00131880701369651.
Walkowiak, T. A., Berry, R. Q., Meyer, J. P., Rimm-Kaufman, S. E., & Ottmar, E. R. (2014). Introducing an observational measure of standards-based mathematics teaching practices: Evidence of validity and score reliability. Educational Studies in Mathematics, 85(1), 109–128. https://doi.org/10.1007/s10649-013-9499-x.
Wragg, E. C. (2012). An introduction to classroom observation. NY: Routledge.
Author information
Authors and Affiliations
Corresponding author
Appendix A
Appendix A
Our literature search was based on the search engines Scopus, Web of Science, and Google Scholar, using the following search terms:
-
Classroom observation AND mathematics.
-
Multiple observation instruments AND mathematics.
-
Multiple observation instruments AND mathematics instruction.
-
Multiple lenses for classroom observations.
-
Multiple lenses for lesson observations.
-
Multiple lenses for observations.
-
Different lenses to capture teaching AND mathematics.
-
Generic teaching practices AND mathematics.
-
Content specific teaching practices AND mathematics.
-
Integrat* generic and content-specific practices.
-
Teacher observations AND mathematics.
Rights and permissions
About this article
Cite this article
Charalambous, C.Y., Praetorius, AK. Studying mathematics instruction through different lenses: setting the ground for understanding instructional quality more comprehensively. ZDM Mathematics Education 50, 355–366 (2018). https://doi.org/10.1007/s11858-018-0914-8
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11858-018-0914-8